幸福理论。 令人头晕的黄油三明治三明治

我继续让哈勃（Habr）的读者熟悉他的著作《幸福理论》（Theory of Happiness）中的章节，并附带“中庸之道的数学基础”。 这本尚未出版的科普书，非常非正式地讲述了数学如何使您以新的意识来审视世界和人们的生活。 它适用于对科学感兴趣的人和对生活感兴趣的人。 而且由于我们的生活是复杂的，而且总体上是不可预测的，因此本书的重点主要放在概率论和数理统计上。 这里没有证明定理，也没有给出科学的基础知识，这绝不是教科书，而是所谓的娱乐科学。 但是，正是这种几乎好玩的方法，使我们得以发展直觉，为学生提供生动的实例来丰富讲座，最后向非数学家和我们的孩子解释我们在干科学中发现了如此有趣的东西。



在本章中，我们研究了三明治的定律，并使用蒙特卡洛方法和维度分析来组织整个研究。 最后，揭穿石油是这种卑鄙定律的起因的流行神话。

三明治跌落的主题既没有引起公众也没有引起研究人员的困扰。 几十年来，已经进行了实验，拍摄了电影，撰写了文章，掉下来的三明治上充斥着传说和错误的结论。 很少有毫无价值的任务会引起如此多的关注，如果您认为所有这些都令人纵容，那么请记住，即使是奖励，对于其解决方案也并不严重。 1995年，罗伯特·马修斯（Robert Matthews）因其著作《跌落三明治，墨菲定律和基本常数》而获得了Shnobel奖，该出版物发表在《欧洲物理学报》上。 尽管有漫画主题和科学界的相应反应，但这是一篇非常有趣的文章，其中对滑动过程进行了透彻的分析并得出了深远的结论：无论出现在大气中的是哪种拟人化的生物，它们都将注定要成为三明治法则。 经过如此无用的研究的胜利，人们可以结束这个话题，但是为什么错过了将有趣且客观有用的方法视为一个有趣问题的例子的机会！

艾达在蒙特卡洛扔三明治！

至少在我们超过两年时，我们很少像硬币一样扔三明治。 通常，我们会不由自主地重复进行相同的实验：最初将黄油放在上面的三明治会从我们手中滑落，或者滑离桌子。 在打滑的过程中，它会扭曲，在空中飞舞，最后扑倒在桌子或地板上。 跌落的初始阶段受到许多参数的影响：手指或桌子表面的摩擦，三明治的初始位置及其初始速度，跌落的高度以及最终的三明治大小。 我们有一个动态系统，具有多个输入参数和一个输出-三明治在地板上的位置。 在系统内部，就像硬币一样，机械定律起作用，这些定律由微分方程描述，并且是确定性的 。 这意味着它们中没有意外-结果仅取决于输入数据，并且通过精确重复参数，我们应该获得相同的结果。 这适用于以微分方程组形式表示的三明治模型，但是真实的三明治，粗糙而又独特，又被真实的人扔到饭店，大街上或沙发上了吗？ 可以通过将随机参数应用于确定性系统的输入来描述现实世界的可变性。

但是，即使仅包含加法和乘法的随机变量代数也不是一件容易的事，但是我们有微分方程！ 我们不会爬入这些令人着迷的荒野，而是使用在许多地区都非常发达的技术- 蒙特卡洛方法 。 它包括积累统计数据，以及通过重复测试各种随机参数来确定某个复杂系统的属性。 我再次强调：所研究的系统不是随机的也不是混沌的，它可以对随机输入数据做出可预测的反应。 在蒙特卡洛方法中，只需要随机性即可，以便有效地整理出尽可能多的选项并查看所有现实的“角度”，从而了解系统的行为。

实际上，我们已经使用了这种方法，在山坡上看着骑自行车的人，并且仍然会通过在办公室安排最后期限并在封闭的社会中分享金钱来使用它。 如前所述，概率与体积或面积的度量之间的一对一对应关系使我们可以使用蒙特卡洛方法进行数值积分。 即将到来的三明治实验的一个特点是，我们将不会对概率分布（精确的或经验的）感兴趣，而会对概率对问题参数的依赖性感兴趣。 我们将寻找问题的答案：在什么情况下可以执行三明治法？ 我们将为动态系统的输入提供各种特定参数，并收集有关掉油和掉油的统计信息。 因此，一系列实验的结果将是一个数字-油掉下来的可能性。

我坚信故意将真实的三明治放在地板上是错误的，因此我们将使用数学建模。 为了解决三明治掉下来的问题，我选择了一种可用的物理世界模拟器来创建在线游戏。 他允许创建一个虚拟的桌子和地板，以及两个三明治。 一个出现在桌子的边缘，另一个出现在“从手指上滑落”，即从点支撑处滑落。 我的权力是设置三明治的初始位置和角度，水平速度（将三明治从桌子上砸下来的情况），摩擦系数，三明治的大小和跌落的高度。 实验看起来像这样：

在物理世界的模拟器中试验虚拟三明治的掉落情况。

在三明治接触地板的那一刻，三明治的角度是固定的，或者说是正交于它的矢量的角度。 该角度正弦的符号将告诉我们机油从哪一侧转向：成功的情况对应于正值，而向下的位置对应于负值。 结果输入到表中，新的虚拟三明治已经准备就绪。 我们设置的任务是：评估当三明治从给定高度掉落时其掉落的可能性。

蒙特卡洛方法假定将随机变量用作参数。 这里值得一说的是什么是随机变量 。 让我们回到数学家和数学结构上。 由于在水上持续不断的兴奋，可以使用哪种结构来模拟在骰子或河流水位上掉落数字的结果？ 一个小时内通过交叉路口的汽车数量如何处理？ 什么结构可以描述电子的状态？ 一方面，这些是一组定义明确的值中的特定数字：例如，对于骨骼， $$$\ {1,2,3,4,5,6 \}$ ，很容易通过实验获得该值。 但是，第二个实验将给出不同的结果，这显然不仅仅是一个数字：今天是一个，明天是另一个。 甚至可能出现一个哲学问题：谈论“河中水位”或汽车数量的确切值是否有意义，因为这些值无法“捕捉”并记录下来？ 从任何意义上说，对随机变量都有确切的了解吗？

通常，在谈论此类随机变量时，它们仅限于平均值，但这是使混淆甚至故意混淆的好方法。 两个数字：平均值和标准差已经比较好了，但这显然不是我们感兴趣的对象的所有信息。 也许这些不是数字，而是集合？ 说，您可以尝试将河流中的水位描述为一个可能的值区间，并考虑到刺激因素，例如，以汽车为例，假设一小时内有1到100辆汽车通过，等等。 但是，很容易看出，可能值的集合也不足够，例如，当重复测量街道上的汽车数量时，一些数字会更频繁地出现，而有些我们根本就不会等待。 在上一章中，我们介绍了概率度量作为概率空间上的函数的方法。 对于随机量，此空间的基本事件将是其定义域的元素，并且度量确定该量的概率分布 。 现在，这是详尽而准确的信息。 一个函数可以用表格，直方图或图表的形式解析地表示或由另一个函数近似表示。 所有这些表示都是同一对象的模型-一个随机变量，而最重要的是，此函数的数学性质与其说是特定的表示类型，不如说是该函数的数学特性。 对于概率分布，属性是不同的：参数的数量，模式的数量，熵，无穷可除性，可加性，稳定性，可积性等。 统计人员从实验中获得的未知随机变量进行建模，统计学家从庞大的已知分布库中精确地定义了属性，而没有选择“最相似”的函数作为与观察到的随机变量的属性最完全一致的函数。 这是统计分析和测试统计假设的技术的精髓，每个接触统计的学生都熟悉该假设 。

从某种意义上说，我们现在有一个相反的问题。 我们需要使用不具有统计数据的随机变量来设置三明治的参数，但是要以这些数量的必要属性为指导。 这是蒙特卡洛方法的重要且有趣的部分，解决方案及其正确性均取决于此。

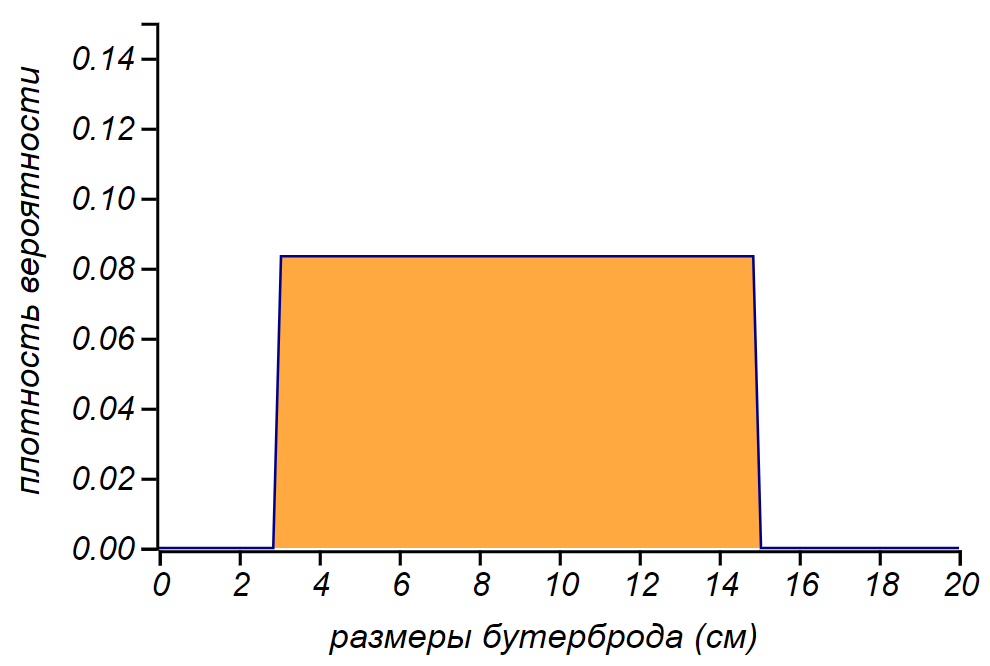1.三明治的尺寸。 他们会是什么？ 大小合理的点心有厘米 $$$3$ 宽，一个好学生的“野兽”可以是几厘米 $$$15$ 。 通常，三明治的尺寸从 $$$6$ 之前 $$$10$ 在这种情况下，实际上遇到毫米或米宽三明治的可能性为零。 我不能再说三明治了，我会接受在指定范围内均匀分布的三明治的大小。 选择是不完美的，但我们发现普通三明治要比细小或大三明治更多。 但是稍后我们将看到可以妥善规避这个薄弱环节。

2.起始位置。 在这里，事不宜迟，我们将设置一个均匀分布，以将三明治移到桌子的边缘（如果它掉落的话）。

3.摩擦系数。 这是无量纲的数量，仅取决于材料。 桌子和桌布不同，手指用不同的强度挤压三明治。 系数范围从 $$$0.01$ 之前 $$$0.5$ ，虽然极小值不太可能，但平均而言， $$$0.3$ 。 任何非负的钟形不对称分布（例如， 伽马分布或对数正态分布）都将对我们有所帮助。

4.初始速度。 我们很少高速推出三明治，大多数情况下我们根本不会扔三明治，但是确实发生了。 关于速度大小的所有已知信息都是正的，可以假设在平均滑动时，我们以平均手的速度移动，即速度约为 $$$0.5$ 米/秒 如果只知道一个数量，那么用指数分布来描述它是合理的（为什么，当我们了解分布的熵时，我们将在后面讨论）。 它的模式为零，因此在没有较大初始速度的情况下掉落的三明治比例将是相当不错的。 在“尾巴”中将是三明治，当从桌子上搅碎面包屑时会不经意地飞向飞行中。

5.我们将固定桌子的高度，从桌子上放下一百个三明治，计算掉下来的油的数量并将其放在桌子上，或在图表上反映出高度的概率。

以下是我们将黄油倒入三明治的可能性：

根据跌落高度的不同，油三明治可能会在不同条件下降落到不同的三明治上。 对于每个高度 $$$100$ 测试。

可以看到一些趋势，但是却出现了非常广泛的趋势。 求平均值时，跌倒高度的概率几乎是独立的，几乎不超过一半。 您可以相信这样的实验吗？ 他是否反驳三明治法律？ 也许我们扔的三明治不够多-嘈杂的数据太多了！ 让我们增加抛出次数，看看会发生什么：

对于大量测试（每个高度500个）计算出的机油滑落到各种三明治上的可能性。

排放量少了，但更清晰可见的是，三明治的定律非常非常弱。 但是我们是否正确执行了实验？ 蒙特卡洛方法看起来很简单：知道自己用什么可怕的数据代替，看看会发生什么。 数学是一句老实话： 她准备回答什么样的问题 。 但是这个答案是否有意义取决于问题。

在开始实验之前，不是像我们的玩具那样像玩具，而是真实的和昂贵的，使用轨道卫星，粒子加速器或一千个含油的真实三明治，必须进行准备工作。 理解如何正确进行实验的有力而优美的方法之一就是分析问题的范围。

我们通过广义坐标，动量和力-物理量对三明治进行建模，而物理量又通过分析力学方程式进行连接。 在物理学中，我们处理并在方程式中替代的定量数量并不“适合”普通数-它们具有附加的结构，称为维 。 如果尺寸量参与其中，并非所有正确的数学表达式都有意义。 假设增加速度和质量没有意义，无法比较力和距离。 但是，我们可以考虑速度和质量的乘积，它已经收到了新的量纲，即动量或动量； 可以对速度求平方并除以距离，从而获得具有加速度尺寸的值。

维度分析和相似性理论诞生于很久以前，即瑞利勋爵（Lord Rayleigh）时代。 它们被用于力学，电动力学，天体物理学和宇宙学，从而有可能以惊人的优雅方式处理复杂的任务。 但是，该领域的研究尚未完成，西班牙数学家Alvaro Raposo仅在2016年对由定量（尺寸）数量形成的结构进行了严格定义 。

尺寸通常对物理公式施加的限制经常被学生和学生视为需要监视的额外混乱。 但是另一方面，逻辑上一致的约束非常有用！ 它们可以过滤掉错误的表达式，可以让您在详细解决方案之前“预测”物理问题的解决方案结构，它们是计划和分析实验数据的强大工具。

但这很有趣。 我们不是使用尺寸而是使用普通数字计算了程序中三明治的下降量。 如何从一个维度“清除”物理量并将其转化为数字？ 为此，我们熟悉熟悉的物理量测量单位 ：所有这些米，磅，分钟和牛顿。 度量单位代表数量的尺寸部分，这给我们留下了一个因素-实际数字，计算机已经可以处理。 例如，所选方向的速度为 $$$60$ km / h可以用数字表示 $$$60$ 。 但是有一个微妙之处：数值表示取决于度量单位的选择。 如果选择其他单位（例如米和秒） ，则相同的速度将由不同的数字表示： $$$16.7$ 。 数字不同，但是数量是一个，并且不取决于我们选择的任何单位。

问题就来了：从某种意义上说，有没有一个“最佳”的单位制？ 事实证明，为此，在解决问题时，需要使用问题中包含的量纲作为度量单位。

在本章中，我们有飞行三明治，在上一个飞行硬币中，我们再举一个飞行示例。 应该如何比较不同鸟类的飞行质量？ 很明显，鸟类的发展速度是不同的：对于鸽子来说- $$$90$ km / h，转瞬即逝- $$$140$ km / h，用于起重机，麻雀或野鸭- $$$50$ 公里/小时，蜂鸟- $$$80$公里/小时 但是所有这些鸟类在大小和飞行方式上都有很大差异。如果说鹦鹉的长度是用鹦鹉来衡量的，而时间是用拍打翅膀的时间来衡量的，那么他们会说自己得到一些速度。您可以将这些鸟可以发展为特征值的速度相除，并获得无量纲的速度，以显示身体在翅膀的一个襟翼中可以走多长时间。这是此比较的结果：

鸟	速度，公里/小时	体长	扫频，1 / s	自身速度，m / s	无量纲速度
迅捷	140	18厘米	5	0.9	43
信鸽	90	30厘米	5	1,5	17
蜂鸟	80	8厘米	200	16	1.4
吊车	50	1米	2,5	2,5	5
绿头鸭	50	40厘米	9	3.6	3.8
麻雀	46	12厘米	13	1,6	8

可以看出，迅捷被认为是最好的飞行者，但是蜂鸟的能量消耗效率低下，但是，这种鸟没有像鸽子那样长时间飞行的任务。当转换成无量纲的数量时，起重机，麻雀和鸭的相同绝对速度会明显不同。这种计算用于模拟真实的大型飞机，在风洞中测试小型模型。如果这两个系统的所有无量纲参数都接近，则可以认为它们在物理上相似并且建模很有意义。我们已经使用这种方法，在Lorenz图上反映相对单位而不是绝对单位。这使我们能够相互比较各种现象和分布。

很明显，当分析三明治的飞行时，最合适的单位制是什么。当然，长度必须以三明治为单位。对于一个时间单位，我们可以将值$$$\sqrt{l/g}$ 在哪里 $$$l$ -三明治的长度，以及 $$$g$-重力加速。桌子的高度不应以米为单位，而应以自己的单位来度量。这样获得结果后，我们可以立即将其推广到小点心和坚固的“硬皮鞋”。因此，我们重复计算，但是在图形上我们以相对单位反映了表格的高度。如果我们做的一切正确，那么对于两个不同尺寸的三明治，我们将获得非常相似的图形。让我们检查一下：

以相对单位计算的油三明治在不同入射高度下降到某个固定值的概率。蓝点对应的是一个5厘米大小的三明治，红点对应的是10厘米

大小。随着测试数量的增加，我们对该云进行了平均，并得到了一个没有意思的答案。为了更清楚地显示方法错误的含义，假设我们要计算三明治掉黄油的概率，随机观察三明治的初始条件，尺寸和高度。这等效于平均一次获得的所有结果。结果，我们获得了自信的中间立场-可能性非常接近$$$1/2$喜欢扔硬币！这是非常合乎逻辑的预期结果，但是完全没有意思。通过对不同大小的大量数据求平均，我们已经接近这个结论。但是，如果建模的目的是识别模式，则将参数的数量减到最少是有意义的。

现在，已清除的数据清楚地表明了均值定律，但是将其限制在一定范围内：$$$2$ 之前 $$$6$ 三明治的大小（从桌子上方的肘部高度到站立的人手臂的高度）。 在此范围之外，三明治在掉落之前更有可能右转。

但是，如果您进一步看并且将三明治扔出窗户怎么办？ 很明显，当从高处坠落时，无论从哪一边掉入三明治都会变成什么，空气阻力都能稳定掉落，但是从理论上讲，我们期望看到什么？ 可能会随着飞行时间的增加而观察到概率的一些波动。 让我们看看：
从高处掉落时油三明治会掉落的可能性。

我们用频率猜测，但是很好奇振幅减小，并且概率波动收敛到 $$$0.5$ 。 它能说什么呢？ 如果随着飞行时间的增加，初始条件偏离的后果变得更加明显，这是否与硬币的效果相同？ 事实证明，在这种情况下，概率均衡的性质是不同的。

多维度分析

无论本书的主题多么轻描淡写，我们都会说数学的语言，他努力寻求精确的解决方案。 蒙特卡洛方法使我们对解决方案有所了解，但这就是所谓的蛮力。 这不像至少一些有趣，而是一种分析解决方案。 对尺寸的分析将使我们能够获得通过蒙特卡洛方法获得的相关性的理论形式。 为此，我们不需要求解微分方程；此外，我们所有的考虑都不会超出完全原始和明显关系的范围。 这就是维分析的魅力，但是，有时看起来像是把戏。 因此，让我们开始吧，为了简单起见，将自己限制为只滑一个长的三明治 $$$l$ 从高度表 $$$H$ 水平速度为零。

1.下降三明治的旋转角度取决于时间和角速度：

$$

$$\ varphi = t \ omega$$

2.角速度等于滑动时间和角加速度的乘积：

$$

$$\ omega = t_0 \ varepsilon$$

3.滑动时间可以用重力加速度和与桌子接触的三明治的一部分长度按以下比例表示：

$$

$$t_0 \ propto \ sqrt {\ frac {l_0} {g}}$$

在这里 $$$l_0$ -躺在桌子上的三明治的长度。 这里我们用符号表示的比例关系 $$$\ proto$ 。 表达方式 $$$y \原型x$ 可以替换为 $$$y = C x$ 在哪里 $$$C$ -一些未知的常数。 我真的很喜欢这种态度。 比例将所有复杂的东西“结合”成一个常数：在旋转过程中重力变化，而在滑动过程中旋转中心变化。 当然，您需要知道所有这些信息才能进行准确的计算，但是结果只是一个无量纲的系数，在我们的分析中它不起作用。 使用一个图标，我们从繁琐的集成中解脱出来。

4.角加速度来自重力加速度，并取决于重力作用的肩部：

$$

$$\ varepsilon \ propto \ frac {g} {l-l_0}$$

再一次的迹象 $$$\ proto$ 允许我们不计算板在其平面内的轴的惯性矩以及不断变化的重力投影（这是另外两个积分）。

5.最后，下降时间取决于工作台的高度和重力加速度：

$$

$$t \ propto \ sqrt {\ frac {H} {g}}$$

6.将所有这些表达式替换为第一个公式，我们得到一个简单的结果：

$$

$$\ varphi \ propto \ sqrt {\ frac {l_0 H} {l（l-l_0）}}，$$

如果您测量三明治中的所有长度，则会变成

$$

$$\ varphi \ propto \ sqrt {\ frac {x h} {1-x}}$$

在这里 $$$l_0 = x l$ 和 $$$H = h l$ 。 好吧，一切都收敛了-角度是无量纲的，并且取决于无量纲的系数。 该角度不取决于时间范围；仅保留几何形状。 分母在以下情况下并不危险 $$$x> 0.5$ 三明治根本不会掉落（我们正在考虑水平速度为零），因此 $$$0 <x <0.5$ 。

夹心将落到哪一侧取决于角度的正弦符号 $$$\ varphi$ 即功能 $$$\ mathrm {sign}（\ sin \ varphi）$ 。 该函数返回 $$$-1$ 对于“加油”的情况 $$$1$ 为“放油”。 如果我们将确定性三明治的范围设置为以下范围，则可以使用该函数来表示确定性三明治掉落的可能性 $$$0$ 之前 $$$1$ ：

$$

$$P _ {\ downarrow}（x，h）= \ frac12 \ left [1+ \ mathrm {sign}（\ sin \ varphi）\ right] = \ frac12 \ left \ {1+ \ mathrm {sign} \ left [ \ sin \ left（C \ sqrt {\ frac {xh} {1-x}} \ right）\ right] \ right \}，$$

箭头符号表示机油的位置。 系数 $$$C$ 出现在概率公式中的表示借助比例符号保持隐藏的所有内容。 这确实是一个非常棘手的举动，它使我们摆脱了繁琐的集成（甚至是三个），但是现在我们如何找出该系数等于多少呢？ 此外，从该实验中，通过一个单独的实验来测量跌落时的角度就足以估算出该值！ 使用模拟器，我很容易发现 $$$C = 2.3$ 。

下一个任务是数学表达初始位置 $$$x$ 可能有所不同。 我们对三明治可能会掉下黄油的可能性感兴趣 $$$x$ 将相等 $$$0.2$ 或 $$$0.4$ 或任何来自 $$$0$ 之前 $$$0.5$ 。 我们使用联合“或”，我们认为这些情况中的每一个都是独立的，并排除了特定实验中的所有其他情况。 回想一下，概率是对概率空间的度量，如果是，则概率是可加的。 这使我们可以简单地添加概率 $$$P _ {\ downarrow}（x，h）$ ，对于所有值 $$$x$ ，再乘以落入特定值范围内的概率。 我们将细分从 $$$0$ 之前 $$$0.5$ 在 $$$n$ 部分，并以总和的形式计算概率估计：

$$

$$P _ {\ downarrow}（h）\ sim \ frac {2} {n} \ sum \ limits_ {i = 0} ^ n P _ {\ downarrow} \ left（\ frac {i} {2n}，h \ right ），$$

这是乘数 $$$2 / n$ 表示随机变量的概率 $$$x$ 进入一块宽度 $$$1 / n$ 。 这是大量分区的结果（ $$$n = 100$ ）以及一系列水平速度为零的数值实验：

三明治从高处掉落时机油掉落的可能性的理论和实验评估。 实验中的初始水平速度为零。

我们之前介绍的解决方案包含更多随机参数，因此它变得更加平滑和接近 $$$0.5$ 。 但是，原则上，可以对更一般的情况进行尺寸分析。

请注意，概率 $$$P _ {\ downarrow}$ 随着增加而接近 $$$h$ 接近 $$$0.5$ 。 这完全不是由于初始误差的不确定性和影响所致。 计算表明，这是将这些值形成的许多谐波相加的结果 $$$x$ 总结时 $$$P _ {\ downarrow}（x，h）$ 。 如果我们忘记了不幸的三明治，请继续安排时间 $$$P _ {\ downarrow}$ ，那么我们看到概率估计将继续波动得如此之近 $$$0.5$ ，逐步争取这一价值。

是否有可能在没有直接计算的情况下找到概率是否会继续收敛到 $$$0.5$ 还是会再次增长？ 在这种现象中，还有一个适用于非平凡和深入的数学的地方。 事实是每个值 $$$x$ 一定的振荡频率相对应，整个集合形成了总功能的所谓频谱 。 如果频谱是离散的，即由单独的频率组成，则总函数（称为傅里叶变换）将是周期性的。 到段上的常数形式的连续光谱 $$$0$ 之前 $$$0.5$ 与减弱的振荡相对应的非周期性函数将相对应。 但是，我们研究了数学- 功能分析的新分支。

伟大的恩里科·费米（Enrico Fermi）是蒙特卡罗方法的祖父（数学家斯坦尼斯拉夫·乌兰姆（Stanislav Ulam被认为是父亲）），他教导他的学生进行简单的评估，弄清楚一块纸或一根手指，我们希望在进行精确解决之前可以得到它。 奇妙的是，如果评估结果正确无误，那么可以清楚地抓住问题的实质，如果不正确，那么这将是更有用的结果-这意味着任务变得比看起来更有趣！

在我们的案例中，简单的估计就足够了；三明治问题不值得更彻底的解决。 蒙特卡洛方法仅向我们显示了该解决方案的提示，而维度分析仅显示了该解决方案的某些一般结构，但它们一起可以向我们展示所需概率的工作原理。 求学使数学家能够在解决方案的蓝图中看到现成的结构，并做出影响深远的假设和结论。

罗伯特·马修斯（Robert Matthews）在其具有里程碑意义的研究中，还使用了维分析来表明三明治法则是基本的。 他的结论是基于这样一个事实，即以后肢为目标的生物的最大高度取决于生物组织的强度特性和重力，该生物的最大目的是将前肢与油作为三明治。 反过来，三明治的特征尺寸应与生物的大小相对应-一些重的行星上的矮人和低重力行星上的土体将自行选择三明治的尺寸。 在这里，我们来谈谈所谓的科学推测 。 这不是以高昂的价格转售任何商品，而是构成逻辑结构基础的可疑假设。 尤其是，我们假设这些生物的手与我们的手具有相似的比例，这是值得商de的。

关于石油和风能

在语言学中，X.L.法则的错误引用 门卡集团：

复杂的问题总是有简单，易于理解的错误解决方案。

您经常会听到三明治的定律应归咎于石油，因为石油比面包浓稠，因此“胜过”。 并且尽管这不适用于我们的书的主题，但我想分析这个问题以结束它。 这样，以后任何人都可以提及“科学家已经证明，油的存在不会影响三明治拍打的那一边！”这​​一事实。

小时候，我们被一个鸽子的苍蝇或尾羽扔了而逗乐，被粘在一块直径一厘米或两厘米高的橡皮泥中。 它飞到了四米高，然后自动旋转优美而平稳地下降，就像一架装有发动机的直升机。 然后我们长大了，我们的乐趣变得不再那么无害了。 我们得到了一个螺母，并从相反的一侧将两个螺栓拧入其中，压缩了压碎的火柴头上的馅。 剩下的只是用一根胶带或一根绳子绑在其中一个螺栓上，正确地解开并向天空飞了十五米。 在秋天，一条轻质的胶带稳定了弹丸的垂直位置，对沥青产生了高质量的冲击，并产生了小小的爆炸，有时甚至将螺母撕成碎片。 （如果您决定与孩子们分享这种童年的经历，请多加注意！）

在这两个实验中，我们看到一支轻笔或一根胶带迅速出现在设备的较重部分上方，并稳定了跌落。 显然，这导致了直观的观点，即厚黄油和轻面包也应以这种方式运行。 想象一个气球：一个更密集的篮子总是位于一个不那么稠密的气球下面。 此外，经验表明，如果用两根手指抓住质量不对称分布的对象的几何中间位置，则该对象会跌落，从而使较重的部分位于底部。

但是，这两种现象在三明治掉落的情况下都不起作用。

让我们从第二个过程开始-“称重”。 我很无聊地指出：“ ...如果采取物体的几何中点..”，这意味着相切点位于形成通过物体重心的旋转轴的特定直线上。 实际上，在这种情况下，稳定位置将是重心在轴下方的位置。 但是，如果手指形成的旋转轴穿过重心，则系统将处于无关紧要的平衡状态-它不会在意它的方向。

是什么使重量轻的羽毛，坚果炸弹或带篮子气球的气球使您以“正确”的方式导航？ 空气 他“握住”我们的物体，使轴经过重心上方。 更确切地说，迎面而来的气流产生了分布在身体区域的力。 此力的条件施加点将位于图形正方形的几何中心附近。 为了更加清楚，我们将绘制作用在条件气球上的力，例如作用在密度不均匀的物体上的力：

使气球进入稳定位置的力。

那三明治呢？

首先，如果我们“关闭”空气，空气只会掉下来。 在自由落体中，身体绕质量中心精确地旋转，因此它没有理由以任何特殊方式旋转。 正如他们在学校说的：“在下降的电梯中，观察到失重。” 三明治中的黄油也很轻。

稠油会影响打滑过程，它将有效地将质心提高到精确的接触上方，并改变角加速度的表达式 $$$l$ 在 $$$\ sqrt {l ^ 2 + d ^ 2} = l \ sqrt {1+ \ delta ^ 2}$ 在哪里 $$$\ delta = d / l$ -三明治的相对厚度。 小值 $$$\ delta$ 这个表达式可以计算为 $$$l（1+ \ delta ^ 2/2）$ 。 正如他们所说，我们获得了二阶效应。 对于宽度与厚度之比为 $$$5$ 到 $$$1$ ，相对变化不超过 $$$2 \％$ 。 这是效果的最大上限，因为我们将质心提高到了三明治的厚度，这相当于无限稠密的油！

现在我们重新打开空气，使油的密度无限地高于面包的密度。 我们有一块薄而密实的板块，上面有一个失重但不透气的降落伞。 当三明治的平面约为水平时，与风成比例的空气阻力作用在其上-气流相互作用的区域： $$$M _ {-} \ propl l ^ 2$ 。 在直立位置，风阻将减小，因此力矩将有所不同： $$$M_ {|} \原型$ 。 这些点的比例： $$$M_ {|} / M _ {-} \ propto \ delta$ 我在这里写了一个比例符号，因为横跨和沿着流的板的阻力系数是不同的，并且它们对我来说是未知的。 但是并不需要它们-已经很清楚，垂直位置的空气效果（即，使油位置不相等）比水平位置的效果弱。 现在我们回想起三明治旋转，这意味着它可以通过末端或通过平面代替流动。 我们可以介绍抵抗力作用的度量。 如果旋转角速度在一个周期内没有显着变化（对于空气而言就是这种情况），则有必要将角动量的变化与力的持续时间成比例地进行测量。 反过来，作用时间与三明治在此期间“扫过”的角度成比例。 结果，测量动作时刻 $$$M_ {|}$ 和 $$$M _ {-}$ 将成比例 $$$M_ {|} \ varphi_ {|}$ 和 $$$M _ {-} \ varphi _ {-}$ 图中显示了扫过末端和平面的角度。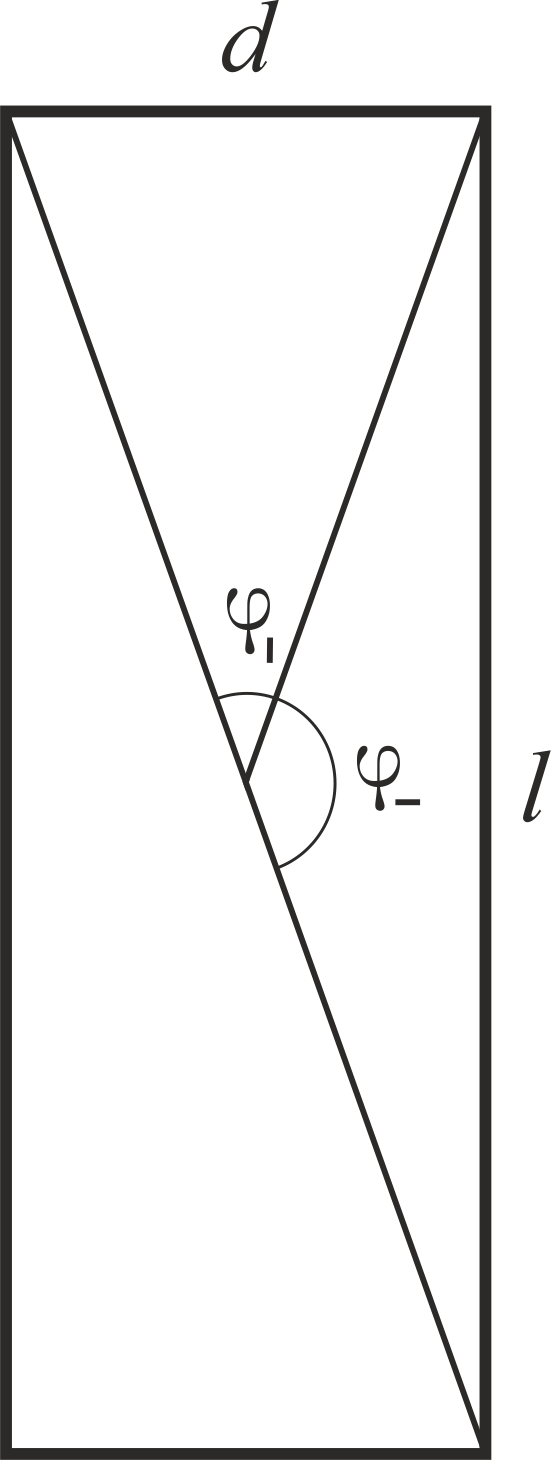 我们可以使用阻力的功作为度量并获得相同的比率。 角度比很容易计算：

$$

$$\ frac {\ varphi_ {|}} {\ varphi _ {-}} = \ frac {\ varphi_ {|}} {\ frac {\ pi} {2}-\ varphi_ {|}}$$

在小 $$$d / l$ ， $$$\ varphi_ {|} \ sim \ delta$ （我们使用小角度切线的属性 $$$10 \％$ 角度较小时的精度 $$$30 ^ \约$ ），因此，我们拥有：

$$

$$\ frac {M_ {|} \ varphi_ {|}} {M _ {-} \ varphi _ {-}} \ sim \ delta \ frac {\ delta} {\ frac {\ pi} {2}-\ delta} \原始\ delta ^ 2。$$

再次证明，对于扁平夹心板的不对称效应受到二次效应的限制。 通常，黄油的密度仅为面包的密度的两倍，质心位移不超过三明治厚度的三分之一，而合理的黄油层则不超过面包的厚度。 这种观察将减少油对 $$$0.2 \％$ 。

如果读者觉得我们现在正在用枪射击麻雀，那么我完全同意他的看法。 但是，首先，我不想听到更多有关“增重”石油的信息，其次，我不想变得毫无根据，其次，我想展示物理学家如何估计代表过程的数量，但没有完整的数据。 当然，在着陆时，黄油会粘在地板上，防止三明治跳起来并再次倾覆，但是我当然不会拆解面包的撞击，弹性变形和跳动的机理。 因此针对此问题进行了大量分析。 她的第二个Shnobelevskaya将不再给予。

$$

$$* * *$$

我们道路的目标并不那么重要：对三明治法则的反驳或辩护，与道路本身一样。 他展示了不同数学方法的组合如何使您能够从不同角度看待问题，并且即使没有详细解决问题的方法也能提供相当准确的知识。 各种数学学科，方法和观点的一致性是数学的强项和美。 回顾玛丽娜·茨维塔耶娃（Marina Tsvetaeva）的精彩话语是恰当的： “我不想有观点，我想有明目 。 ” 对数学各个领域的研究可以为研究人员提供真正的“体积”多维视野，使您可以查看看似封闭和隐藏的知识空间。