使用QML地图构建航空-第1部分

相当长一段时间以来，我一直在使用QML构建图形界面，但是到目前为止，还没有机会使用Qt Location API和QML Map在真实的项目中工作。
因此，尝试将此组件用于构建气道变得很有趣。
切割器下方是编辑器实现的描述，用于在地图上创建类似的路径：



为了简化实现，我们的飞机在2D平面中以相同的高度飞行。 速度和允许的过载是固定的-920 km / h和3g，这给出了转弯半径

$$

$$R = \ frac {v ^ 2} {G} = 21770 m$$

轨迹包括以下部分：

其中S是动作的开始（这是上一个动作的出口点），M是转弯的起点，E是转弯的出口，F是终点（下一个动作是M）。

为了计算轨迹的进出点，我使用了圆的切线方程 ，计算结果非常麻烦，我相信它可以变得更简单。

void Manoeuvre::calculate() { // General equation of line between first and middle points auto A = mStart.y() - mMiddle.y(); auto B = mMiddle.x() - mStart.x(); // Check cross product sign whether final point lies on left side auto crossProduct = (B*(mFinal.y() - mStart.y()) + A*(mFinal.x() - mStart.x())); // All three points lie on the same line if (isEqualToZero(crossProduct)) { mIsValid = true; mCircle = mExit = mMiddle; return; } mIsLeftTurn = crossProduct > 0; auto lineNorm = A*A + B*B; auto exitSign = mIsLeftTurn ? 1 : -1; auto projection = exitSign*mRadius * qSqrt(lineNorm); // Center lies on perpendicular to middle point if (!isEqualToZero(A) && !isEqualToZero(B)) { auto C = -B*mStart.y() - A*mStart.x(); auto right = (projection - C)/A - (mMiddle.x()*lineNorm + A*C) / (B*B); mCircle.ry() = right / (A/B + B/A); mCircle.rx() = (projection - B*mCircle.y() - C) / A; } else { // Entering line is perpendicular to either x- or y-axis auto deltaY = isEqualToZero(A) ? 0 : exitSign*mRadius; auto deltaX = isEqualToZero(B) ? 0 : exitSign*mRadius; mCircle.ry() = mMiddle.y() + deltaY; mCircle.rx() = mMiddle.x() + deltaX; } // Check if final point is outside manouevre circle auto circleDiffX = mFinal.x() - mCircle.x(); auto circleDiffY = mFinal.y() - mCircle.y(); auto distance = qSqrt(circleDiffX*circleDiffX + circleDiffY*circleDiffY); mIsValid = distance > mRadius; // Does not make sence to calculate futher if (!mIsValid) return; // Length of hypotenuse from final point to exit point auto beta = qAtan2(mCircle.y() - mFinal.y(), mCircle.x() - mFinal.x()); auto alpha = qAsin(mRadius / distance); auto length = qSqrt(distance*distance - mRadius*mRadius); // Depends on position of final point find exit point mExit.rx() = mFinal.x() + length*qCos(beta + exitSign*alpha); mExit.ry() = mFinal.y() + length*qSin(beta + exitSign*alpha); // Finally calculate start/span angles auto startAngle = qAtan2(mCircle.y() - mMiddle.y(), mMiddle.x() - mCircle.x()); auto endAngle = qAtan2(mCircle.y() - mExit.y(), mExit.x() - mCircle.x()); mStartAngle = startAngle < 0 ? startAngle + 2*M_PI : startAngle; endAngle = endAngle < 0 ? endAngle + 2*M_PI : endAngle; auto smallSpan = qFabs(endAngle - mStartAngle); auto bigSpan = 2*M_PI - qFabs(mStartAngle - endAngle); bool isZeroCrossed = mStartAngle > endAngle; if (!mIsLeftTurn) { mSpanAngle = isZeroCrossed ? bigSpan : smallSpan; } else { mSpanAngle = isZeroCrossed ? smallSpan : bigSpan; } } 

完成了对轨迹数学模型的错误估计后，我们将继续直接处理地图。 在QML地图上构建折线的自然选择是将MapPolyline直接添加到地图。

 Map { id: map plugin: Plugin { name: "osm" } MapPolyline { path: [ { latitude: -27, longitude: 153.0 }, ... ] } } 

最初，我想为用户提供“动态”模拟路线的每个后续部分的机会-创建光标后面的轨迹效果。



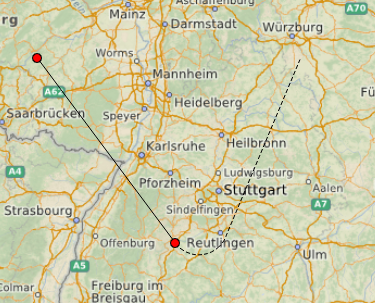
移动光标时更改路径是一项相当昂贵的操作，因此我尝试使用显示的初步“像素”路径，直到用户最终保存路径为止。

 Repeater { id: trajectoryView model: flightRegistry.hasActiveFlight ? flightRegistry.flightModel : [] FlightItem { anchors.fill: parent startPoint: start endPoint: end manoeuvreRect: rect manoeuvreStartAngle: startAngle manoeuvreSpanAngle: spanAngle isVirtualLink: isVirtual } } 

FlightItem是QQuickItem ，并且QAbstractListModel flightModel允许您在更改数据以进行机动时更新轨迹的必要部分。

 QVariant FlightModel::data(const QModelIndex &index, int role) const { if (!index.isValid()) { return QVariant(); } switch (role) { case FlightRoles::StartPoint: return mFlight->flightSegment(index.row()).line().p1(); case FlightRoles::EndPoint: return mFlight->flightSegment(index.row()).line().p2(); ... } 

这样的实时更新使您可以警告用户有关无法实现的操作。



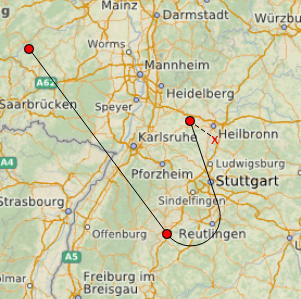
仅在完成气管的创建后（例如，单击鼠标右键），该路线才最终会作为GeoPath添加到QML地图中，并可能具有地理参考（直到此刻地图无法移动和缩放，像素才不了解经度和纬度）。
为了将像素段重新计算为地理坐标，对于初学者，我们需要为每个操纵使用操纵入口点（我们的点S）本地的坐标系。

 QPointF FlightGeoRoute::toPlaneCoordinate(const QGeoCoordinate &origin, const QGeoCoordinate &point) { auto distance = origin.distanceTo(point); auto azimuth = origin.azimuthTo(point); auto x = qSin(qDegreesToRadians(azimuth)) * distance; auto y = qCos(qDegreesToRadians(azimuth)) * distance; return QPointF(x, y); } 

重新计算已经完成的米的机动之后，有必要进行反向操作并知道点S的地理参考，以将米转换为纬度-经度。

 QGeoCoordinate FlightGeoRoute::toGeoCoordinate(const QGeoCoordinate &origin, const QPointF &point) { auto distance = qSqrt(point.x()*point.x() + point.y()*point.y()); auto radianAngle = qAtan2(point.x(), point.y()); auto azimuth = qRadiansToDegrees(radianAngle < 0 ? radianAngle + 2*M_PI : radianAngle); return origin.atDistanceAndAzimuth(distance, azimuth); } 

从正式的角度来看，当然不可能认为我们的“像素”和“米”轨迹是相同的，但是对我来说，展望未来并向用户展示会发生什么（或者如果飞机不像这样飞行则不会发生）似乎非常可口。他下次会点击。 最终确定轨迹之后（它在颜色和透明度上与像素之一略有不同，因为即使是静态虚线在地图上看起来也不是很平滑）。



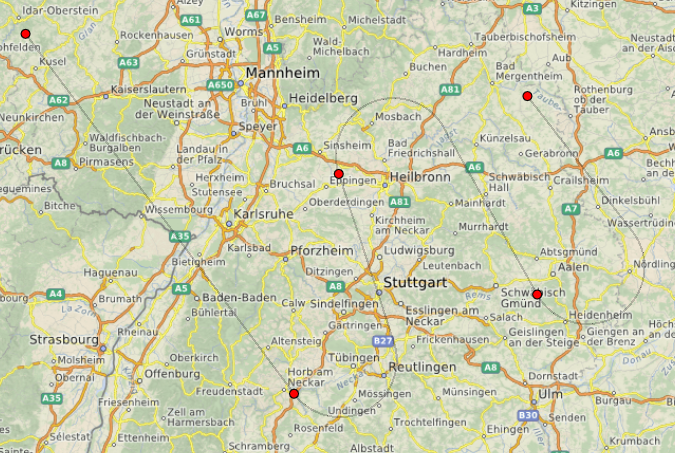此处提供了源；对于编译，我使用了Qt 5.11.2。

在下一部分中，我们将教我们的编辑器移动轨迹的参考点，以及保存/打开现有路线，以便随后模拟飞机的运动。