这是第二篇有关对海上搜寻船只比赛的材料进行分析和研究的文章。 但是现在我们将研究训练序列的属性。 让我们尝试查找多余的信息,源数据中的冗余并将其删除。

本文也是出于好奇和闲置兴趣的结果,在实践中什么也没有遇到,对于实际任务几乎没有复制粘贴的内容。 这是对培训顺序属性的一项小研究-给出了作者的推理和代码,您可以自己检查/补充/更改所有内容。
kaggle海洋搜索比赛最近结束了。 空中客车公司建议分析有船和无船的海洋卫星图像。 如果uint8,则总共192555张图片768x768x3-340,720,680,960字节,这是大量信息,并且模糊地怀疑并非所有图片都需要训练网络,并且在这种信息量中,重复和冗余是显而易见的。 训练网络时,习惯上会分离一些数据,而不在训练中使用它们,而是使用它来验证训练的质量。 并且,如果一个海洋和同一片海域陷入了两个不同的图像中,而一个图像又落入了训练序列中,而另一图像又落入了验证序列中,那么验证将失去意义,网络将受到重新训练,我们将不会检查网络的泛化信息的能力,因为数据是相同的。 应对这种现象需要参与者的GPU花费大量时间和精力。 像往常一样,优胜者和获奖者都不会急于向他们的粉丝们展示精通的秘密并列出代码,并且没有学习和学习它的方法,因此我们将继续学习该理论。
一个简单的视觉检查显示确实有太多数据,同一条海道变成了不同的图片,请看示例




出于这个原因,我们对真实数据不感兴趣,存在很多虚假的依赖关系,与我们不必要的连接,不良的标记以及其他缺点。
在
第一篇文章中,我们研究了带有椭圆和噪点的图片,我们将继续对其进行研究。 这种方法的优点是,如果您发现在任意图片集上训练的网络的任何吸引人的功能,则不清楚这是网络属性还是训练集的属性。 来自现实世界的序列的统计参数未知。 最近,大师Pleskov Pavel
paske57 谈到 ,如果自己亲自研究数据(例如查看照片元数据)是一件
好事,有时候赢得图片的分类/分类很容易。 并且不能保证在实际数据中不存在这种非自愿地依赖关系。 因此,为了研究网络的属性,我们使用椭圆和矩形拍照,并使用计算机的随机数生成器(其具有伪随机生成器,该伪随机生成器具有基于其他非数字算法和物质物理特性的生成器来确定位置,颜色和其他参数,但是我们将不在本文中讨论)。
因此,以sea
np.random.sample()* 0.75为例 ,我们不需要波浪,风,海岸和其他隐藏的图案和面孔。 船/椭圆也将涂上相同的颜色,以区分海与船和干扰物,向海或船/干扰物添加0.25,它们都将是相同的形状-不同大小和方向的椭圆。 干扰也只会是与椭圆相同颜色的矩形-这很重要,信息和干扰背景下的相同颜色的干扰也很重要。 我们将仅对颜色进行少量更改,并且将为每张图片和每个椭圆/矩形运行
np.random.sample() ,即 椭圆/矩形的背景和颜色均不重复。 文本中还有用于创建图片/蒙版的程序代码以及十个随机选择的对的示例。
以一个非常普通的网络版本(您可以使用自己喜欢的网络)为例,尝试识别并显示大型训练序列的冗余,从而至少获得某种定性和定量的冗余特征。 即 作者认为,许多GB的训练序列实际上是多余的,有许多不必要的图片,不需要加载数十个GPU并进行不必要的计算。 数据的冗余不仅体现在同一部分显示在不同的图片中,而且还体现在这些数据中信息的冗余上,而不是那么多。 即使未正确重复,数据也可能是冗余的。 请注意,这不是对信息及其充分性或冗余性的严格定义。 我们只想了解可以减少多少训练,可以从训练序列中剔除哪些图片以及多少图片足以接受(我们会在程序中自行设置精度)训练。 这是一个特定的程序,一个特定的数据集,作为障碍,在带有三角形的椭圆上,有可能没有任何效果,在带有矩形的椭圆上(我的假设是,一切都将相同并且相同。但是我们现在不对其进行检查) ,我们不进行分析,也不证明定理)。
因此,鉴于:
- 图片/遮罩对的学习顺序。 我们可以生成任意数量的图片/蒙版对。 我将立即回答问题-为什么颜色和背景是随机的? 我将简单,简要,清楚而全面地回答我非常喜欢它,不需要边界形式的额外实体;
- 该网络是普通的,普通的U型网络,经过稍加修改并广泛用于细分。
测试思路:
- 与实际任务一样,在构造的序列中使用的是千兆字节的数据。 作者认为训练序列的大小不是那么关键,应该没有很多数据,但是它们应该包含“很多”信息。 这样的数量,一万对图片/掩模,是没有必要的,网络将从更少的数据中学习。
让我们开始,选择10,000对,并仔细考虑它们。 我们将从该训练序列中挤出所有水,所有不必要的碎屑,并将所有干燥残留物使用并付诸实践。
现在,您可以检查自己的直觉,并假设在10,000对中有多少对足以训练和预测另一对,而且还创建了10,000对对的序列,其准确性超过0.98。 比较后写在纸上。
为了实际使用,请考虑到人为选择的海洋和船只,这是
np.random.sample() 。
我们加载库,确定图片数组的大小import numpy as np import matplotlib.pyplot as plt %matplotlib inline import math from tqdm import tqdm from skimage.draw import ellipse, polygon from keras import Model from keras.optimizers import Adam from keras.layers import Input,Conv2D,Conv2DTranspose,MaxPooling2D,concatenate from keras.layers import BatchNormalization,Activation,Add,Dropout from keras.losses import binary_crossentropy from keras import backend as K import tensorflow as tf import keras as keras w_size = 128 train_num = 10000 radius_min = 10 radius_max = 20
确定损失和准确性函数 def dice_coef(y_true, y_pred): y_true_f = K.flatten(y_true) y_pred = K.cast(y_pred, 'float32') y_pred_f = K.cast(K.greater(K.flatten(y_pred), 0.5), 'float32') intersection = y_true_f * y_pred_f score = 2. * K.sum(intersection) / (K.sum(y_true_f) + K.sum(y_pred_f)) return score def dice_loss(y_true, y_pred): smooth = 1. y_true_f = K.flatten(y_true) y_pred_f = K.flatten(y_pred) intersection = y_true_f * y_pred_f score = (2. * K.sum(intersection) + smooth) / (K.sum(y_true_f) + K.sum(y_pred_f) + smooth) return 1. - score def bce_dice_loss(y_true, y_pred): return binary_crossentropy(y_true, y_pred) + dice_loss(y_true, y_pred) def get_iou_vector(A, B):
我们将使用
第一篇文章中的指标。 让我提醒读者,我们将预测像素的遮罩-这是“海”或“船”,并评估预测的真实性或虚假性。 即 以下四个选项是可能的-我们正确地预测像素是“海”,正确地预测像素是“船”,或者在预测“海”或“船”时出错。 因此,对于所有图片和所有像素,我们估计所有四个选项的数量并计算结果-这将是网络的结果。 错误的预测越少越准确,结果越准确,网络越好。
为了进行研究,让我们选择经过精心研究的U-net,它是用于图像分割的出色网络。 选择了不太经典的U-net版本,但想法是相同的,网络对图片执行了非常简单的操作-它通过逐步进行变换来减小图片的大小,然后尝试从压缩图像中恢复掩码。 即 在我们的案例中,图片的尺寸被设为16x16,然后我们尝试使用之前所有压缩层中的数据来还原蒙版。
我们将网络视为“黑匣子”,而不会研究网络内部发生的情况,权重如何变化以及如何选择渐变-这是另一项研究的主题。
带块的U网 def convolution_block(x, filters, size, strides=(1,1), padding='same', activation=True): x = Conv2D(filters, size, strides=strides, padding=padding)(x) x = BatchNormalization()(x) if activation == True: x = Activation('relu')(x) return x def residual_block(blockInput, num_filters=16): x = Activation('relu')(blockInput) x = BatchNormalization()(x) x = convolution_block(x, num_filters, (3,3) ) x = convolution_block(x, num_filters, (3,3), activation=False) x = Add()([x, blockInput]) return x
生成图片/遮罩对的功能。 在填充有随机噪声的128x128彩色图片上,该噪声是从0.0 ... 0.75或0.25..1.0两个范围中随机选择的。 在图片中随机放置一个随机取向的椭圆,并在同一位置放置一个矩形。 我们检查它们是否相交,并在必要时将矩形移到侧面。 每次我们重新计算海/船的着色值。 为了简单起见,我们将带有图片的遮罩放在一个阵列中,作为第四种颜色,即 红色,绿色,蓝色,面具,更容易。
def next_pair(): img_l = (np.random.sample((w_size, w_size, 3))* 0.75).astype('float32') img_h = (np.random.sample((w_size, w_size, 3))* 0.75 + 0.25).astype('float32') img = np.zeros((w_size, w_size, 4), dtype='float') p = np.random.sample() - 0.5 r = np.random.sample()*(w_size-2*radius_max) + radius_max c = np.random.sample()*(w_size-2*radius_max) + radius_max r_radius = np.random.sample()*(radius_max-radius_min) + radius_min c_radius = np.random.sample()*(radius_max-radius_min) + radius_min rot = np.random.sample()*360 rr, cc = ellipse( r, c, r_radius, c_radius, rotation=np.deg2rad(rot), shape=img_l.shape ) p1 = np.rint(np.random.sample()* (w_size-2*radius_max) + radius_max) p2 = np.rint(np.random.sample()* (w_size-2*radius_max) + radius_max) p3 = np.rint(np.random.sample()* (2*radius_max - radius_min) + radius_min) p4 = np.rint(np.random.sample()* (2*radius_max - radius_min) + radius_min) poly = np.array(( (p1, p2), (p1, p2+p4), (p1+p3, p2+p4), (p1+p3, p2), (p1, p2), )) rr_p, cc_p = polygon(poly[:, 0], poly[:, 1], img_l.shape) in_sc_rr = list(set(rr) & set(rr_p)) in_sc_cc = list(set(cc) & set(cc_p)) if len(in_sc_rr) > 0 and len(in_sc_cc) > 0: if len(in_sc_rr) > 0: _delta_rr = np.max(in_sc_rr) - np.min(in_sc_rr) + 1 if np.mean(rr_p) > np.mean(in_sc_rr): poly[:,0] += _delta_rr else: poly[:,0] -= _delta_rr if len(in_sc_cc) > 0: _delta_cc = np.max(in_sc_cc) - np.min(in_sc_cc) + 1 if np.mean(cc_p) > np.mean(in_sc_cc): poly[:,1] += _delta_cc else: poly[:,1] -= _delta_cc rr_p, cc_p = polygon(poly[:, 0], poly[:, 1], img_l.shape) if p > 0: img[:,:,:3] = img_l.copy() img[rr, cc,:3] = img_h[rr, cc] img[rr_p, cc_p,:3] = img_h[rr_p, cc_p] else: img[:,:,:3] = img_h.copy() img[rr, cc,:3] = img_l[rr, cc] img[rr_p, cc_p,:3] = img_l[rr_p, cc_p] img[:,:,3] = 0. img[rr, cc,3] = 1. return img
让我们创建一个训练对的序列,请参阅随机10
_txy = [next_pair() for idx in range(train_num)] f_imgs = np.array(_txy)[:,:,:,:3].reshape(-1,w_size ,w_size ,3) f_msks = np.array(_txy)[:,:,:,3:].reshape(-1,w_size ,w_size ,1) del(_txy)
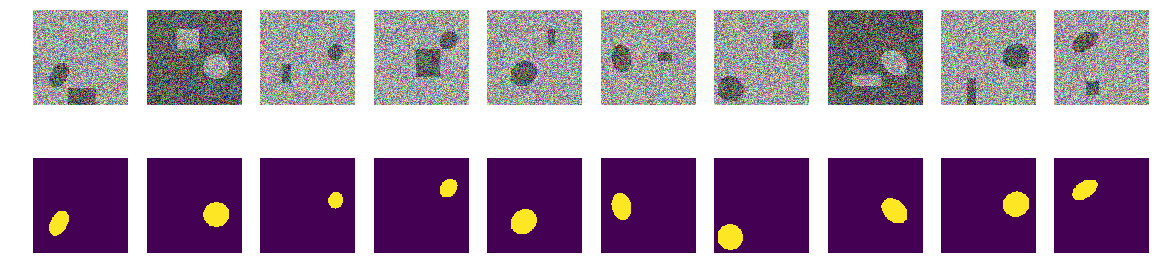
第一步。 让我们尝试以最少的训练
实验的第一步很简单,我们正在尝试训练网络以仅预测11张第一张图片。
batch_size = 10 val_len = 11 precision = 0.85 m0_select = np.zeros((f_imgs.shape[0]), dtype='int') for k in range(val_len): m0_select[k] = 1 t = tqdm() while True: fit = model.fit(f_imgs[m0_select>0], f_msks[m0_select>0], batch_size=batch_size, epochs=1, verbose=0 ) current_accu = fit.history['my_iou_metric'][0] current_loss = fit.history['loss'][0] t.set_description("accuracy {0:6.4f} loss {1:6.4f} ".\ format(current_accu, current_loss)) t.update(1) if current_accu > precision: break t.close()
accuracy 0.8636 loss 0.0666 : : 47it [00:29, 5.82it/s]我们从初始序列中选择了前11个,并在它们上面训练了网络。 现在,网络是专门存储这些图片还是进行汇总都无所谓,主要是它可以按照我们需要的方式识别这11张图片。 根据所选的数据集和准确性,网络训练可以持续很长时间。 但是我们只有几次迭代。 我再说一遍,对于我们现在来说网络学习或学习的方式和知识并不重要,主要是它已达到既定的预测准确性。
现在开始主要实验
我们将从构建的序列中获取新的图片/遮罩对,并尝试由受过训练的网络在已选择的序列上进行预测。 刚开始时,只有11对图像/遮罩和网络训练,也许不是很正确。 如果在新对中以可接受的精度预测图片中的掩码,那么我们将丢弃该对,它没有网络的新信息,它已经知道并可以从该图片中计算出掩码。 如果预测的准确性不足,则我们将此图像加遮罩添加到序列中,并开始训练网络,直到在所选序列上获得可接受的准确性结果为止。 即 该图片包含新信息,我们将其添加到我们的训练序列中,并通过训练提取其中包含的信息。
batch_size = 50 t_batch_size = 1024 raw_len = val_len t = tqdm(-1) id_train = 0
Accuracy 0.9830 loss 0.0287 selected img 271 tested img 9949 : : 1563it [14:16, 1.01it/s]
在此,精度是指“精度”,而不是标准的keras度量,子例程“ my_iou_metric”用于计算精度。 观察被调查和添加的图片的准确性和数量非常有趣。 最初,几乎所有图片/遮罩对都是由网络添加的,大约70处开始丢弃。 接近8000投掷几乎所有的对。
检查网络选择的视觉随机对:
fig, axes = plt.subplots(2, 10, figsize=(20, 5)) t_imgs = f_imgs[m0_select>0] t_msks = f_msks[m0_select>0] for k in range(10): kk = np.random.randint(t_msks.shape[0]) axes[0,k].set_axis_off() axes[0,k].imshow(t_imgs[kk]) axes[1,k].set_axis_off() axes[1,k].imshow(t_msks[kk].squeeze())
没有什么特别的或超自然的:
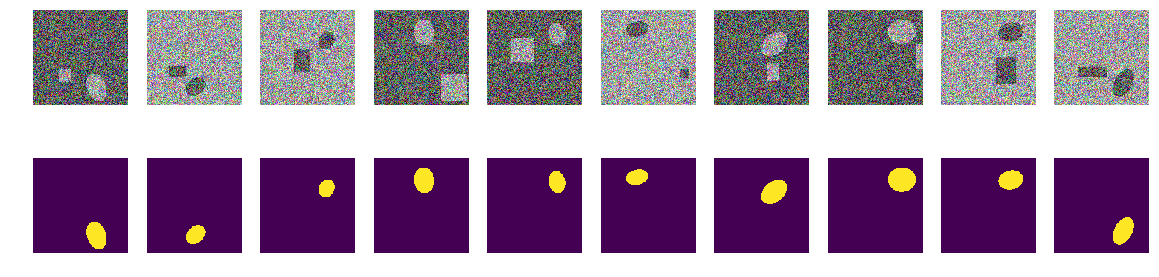
这些是网络在训练的不同阶段选择的对。 当网络从该序列中接收到输入对时,它无法以指定的精度计算掩码,并且该对已包含在训练序列中。 但是没有什么特别的普通图片。
验证结果和准确性
让我们检查网络训练程序的质量,确保质量不明显取决于初始序列的顺序,为此,我们将图像/遮罩对的初始序列混合在一起,以相同的方式优先选择其他11对,训练网络并切断多余的部分。
sh = np.arange(train_num) np.random.shuffle(sh) f0_imgs = f_imgs[sh] f0_msks = f_msks[sh] model.compile(loss=bce_dice_loss, optimizer="adam", metrics=[my_iou_metric]) model.summary()
锻炼代码 batch_size = 10 val_len = 11 precision = 0.85 m0_select = np.zeros((f_imgs.shape[0]), dtype='int') for k in range(val_len): m0_select[k] = 1 t = tqdm() while True: fit = model.fit(f0_imgs[m0_select>0], f0_msks[m0_select>0], batch_size=batch_size, epochs=1, verbose=0 ) current_accu = fit.history['my_iou_metric'][0] current_loss = fit.history['loss'][0] t.set_description("accuracy {0:6.4f} loss {1:6.4f} ".\ format(current_accu, current_loss)) t.update(1) if current_accu > precision: break t.close()
accuracy 0.8636 loss 0.0710 : : 249it [01:03, 5.90it/s]
batch_size = 50 t_batch_size = 1024 raw_len = val_len t = tqdm(-1) id_train = 0
Accuracy 0.9890 loss 0.0224 selected img 408 tested img 9456 : : 1061it [21:13, 2.16s/it]
结果并不显着取决于原始序列对的顺序。 在前一种情况下,网络选择了271,现在选择了408,如果您将其混合使用,则网络可以选择其他数量。 我们不会检查,笔者认为总会少于10,000。
在新的独立序列上检查网络预测的准确性
_txy = [next_pair() for idx in range(train_num)] test_imgs = np.array(_txy)[:,:,:,:3].reshape(-1,w_size ,w_size ,3) test_msks = np.array(_txy)[:,:,:,3:].reshape(-1,w_size ,w_size ,1) del(_txy) test_pred_0 = model.predict(test_imgs) t_val_0 = get_iou_vector(test_msks,test_pred_0) t_val_0
0.9927799999999938
总结与结论
因此,我们能够从10,000对中选择少于三到四百个,预测准确度为0.99278,我们将所有包含至少一些有用信息的对剔除掉,剩下的全部剔除。 我们没有调整训练序列的统计参数,也没有增加信息的可重复性,等等。 并且根本没有使用统计方法。 我们拍一张照片,其中仍然包含网络未知的信息,然后将所有信息挤出网络的负担。 如果网络至少遇到一张“神秘”图片,那么它将在业务中全部使用。
总共271对图片/遮罩对包含用于预测10,000对的信息,每对对的准确度至少为0.8075,即,整个序列的总准确度较高,但是在每张图片中,其总准确度不低于0.8075,我们没有没有图片我们可以预测,并且知道该预测的下边界。 (当然,在这里,作者自吹自without,如果没有这个,这篇文章怎么不会验证这个说法,大约是0.8075,还是证据,但很可能是真的)
要训练网络,不需要将即将到来的所有内容加载到GPU中,您可以拉出训练的核心,并在训练开始时在其上训练网络。 当您获得新图片时,您可以手动标记出网络无法预测的图片并将其添加到火车的核心,从而对网络进行重新培训以从新图片中压缩所有信息。 而且没有必要单独选择一个验证序列;我们可以假定除选定的序列以外的所有其他内容都是一个验证序列。
在数学上并不严格,但很重要。 可以肯定地说,每个图片/遮罩对都包含“很多”信息。 每对都包含“大量”信息,尽管在大多数图片/遮罩对中,信息是相交或重复的。 271个图片/遮罩对中的每对都包含对于预测必不可少的信息,并且不能简单地将其丢弃。
好吧,关于折痕的一句话,许多专家和kagglers将训练顺序分为折痕,然后分别训练,并结合以更棘手的方式获得的结果。 在我们的情况下,您也可以将其分成多个折叠,如果从10,000个中删除271对,则可以在其余根中创建一个新的根序列,这显然会提供不同但可比的结果。 您可以简单地混合并取其他前11个,如上所示。
本文提供了一个代码,并显示了如何训练U-net进行图像分割。 这是一个具体的例子,在本文中,有意地没有对其他网络,其他序列进行泛化,也没有严格的数学原理,一切都在“指尖”上讲述和展示。 只是一个示例,说明如何在达到可接受的准确性的同时学习网络。