当我查看用户
xcont的帖子时,发现了这种模式。 偶然发现
该出版物后 ,我提请注意一个事实,即不仅根据斐波那契数据的规模增加,还会重复出现模式。

我想知道这些模式中是否有一个模式。 但是只有2个参数
x和
y ,我决定需要指定其他东西,在所获得的所有模式中都相同。 然后我注意到,如果我们在该字段上取前4个正方形,则无论如何,如果行行进,我们将获得3个用于模式开头的选项:
上(↑)

下(↓)

还是不走*(-)

为了进行指定,我决定使用这些符号↑,↓,有条件地将其称为自旋(如粒子的自旋)。 在这里,我开始创建一个表,将这些自旋对
x ,
y的依赖性。
首先,让我们看一下是否有一个模式,如果只改变
y ,
x取4

现在关于属性
我们看到一系列旋转
-↑-↓-↑-↓-↑-↓模式以一定顺序重复
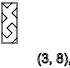
y = 3,7,11 ...(
↑ )
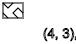
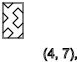
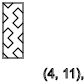
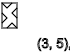
y = 5,9,13 ...(
↓ )
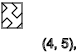
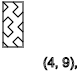
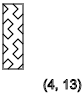
y = 2,4,6,8,10,12 ...(
- )
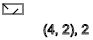
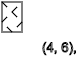
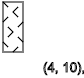
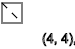
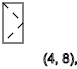
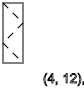
如果
x = 3,我们得到相同的结果,我们看到一系列旋转
↑-↓↑-↓↑-↓↑-↓↑
y = 2,5,8,11 ...(
↑ )
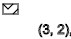
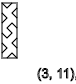
y = 4,7,10,13 ...(
↓ )

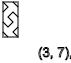
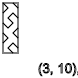
y = 3,6,9,12 ...(
- )
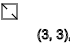
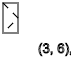
我以为我可以将这些序列系统化,并编制出这些旋转的表格,这就是我得到的。
我向您介绍“黑色表”。
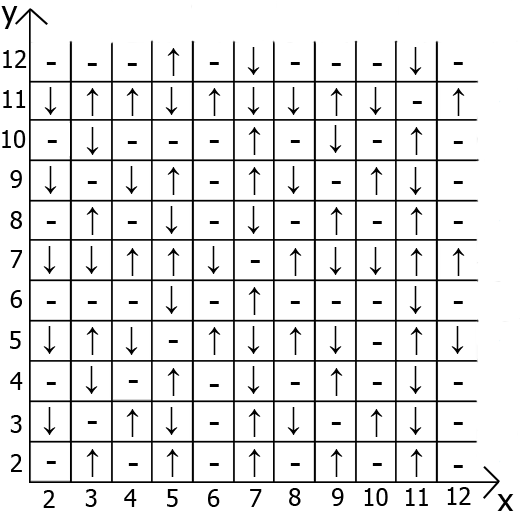
最有趣的是,该表具有其依赖性和属性。
首先,我们导出几个公式:
→如果
x是偶数而
y是偶数--,则
x x y或
y x x-- x = y→-
x = y + 1→↑
x = y-1→↓
现在关于表本身的属性,如果我们将x = y作为参考点,则在任何方向上我们都有镜面反射的序列(用红线和绿线表示)。
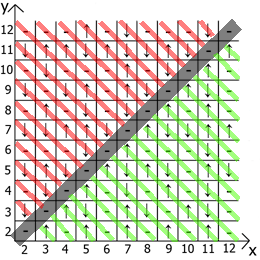
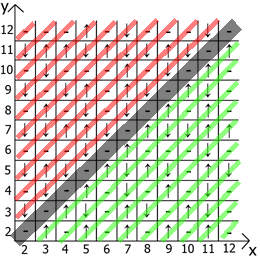
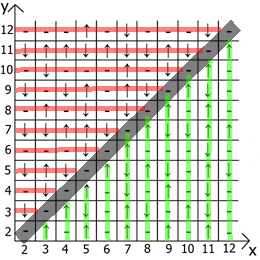
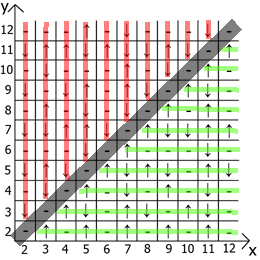
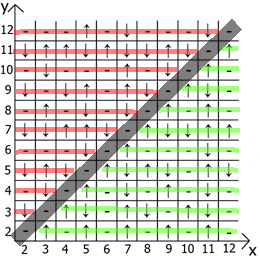
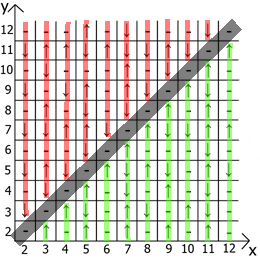

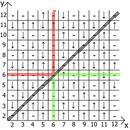
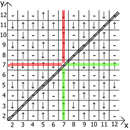
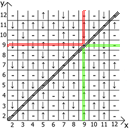
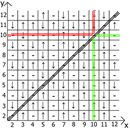
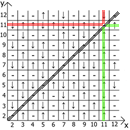
居然找到用途和用途。 我有一个最多12张桌子,因为起初我是在纸上做这些事情的。

但是,使用
JavaScript算法,您自己可以检查更大的值。
PS我不知道如何使用它,但是也许这种算法可以应用在量子计算机上。
链接:
一和
二 。