雪花，Romanesco卷心菜，海星，闪电和树木有什么共同点？ 您不会立即这么说，但是从数学角度来看，所有这些对象都有一个共同的特征-分形。 在数学眼中，我们世界上的所有事物都遵守“科学女王”的定律。 可以说，任何现象，过程或对象都可以用数学形式表示，从而可以从一个新的角度对其进行分析。 多年来，科学家一直在尝试创建基因，它们之间的关系以及涉及它们的过程的完美数学表示。 今天，我们将讨论从癌症的角度来看，分形如何为全新的人类基因数学模型奠定基础。 分形是什么，为什么它对遗传学家和数学家如此重要，新的数学模型如何帮助现代医学？ 我们将在研究小组的报告中寻找答案。 走吧
理论撤退首先，有必要简要地弄清楚什么是分形以及如何食用它。
分形是具有自相似属性的集合。 简而言之，当某物包含其自身的多个迷你副本时。
分形存在于各种物理现象中：从扩散到湍流。 这可以称为分形的自然表现。 人们还发现分形的用途：计算机图形学，无线电工程，网络技术等。
电影《奇异博士》（Doctor Strange，2016年）中的分形非常丰富多彩，当长者在平行尺寸的短途旅行中派主角时。
视线有些不愉快，但清楚地表明了它的分形性。即使在超市的货架上，您也可以找到分形的表现形式，例如罗曼斯科白菜或花椰菜。
如果考虑到具有分形性质的集合的类型很多，那么可以说，我们周围的几乎所有事物都以一种或另一种方式与分形有关。 人体，尤其是其基因，也不例外。 由于可以通过对组分进行分类来从数学上解释分形，因此在人类基因上使用这种模型可以极大地帮助您了解人体中发生的各种过程，包括各种疾病，病理和其他不愉快的事情。
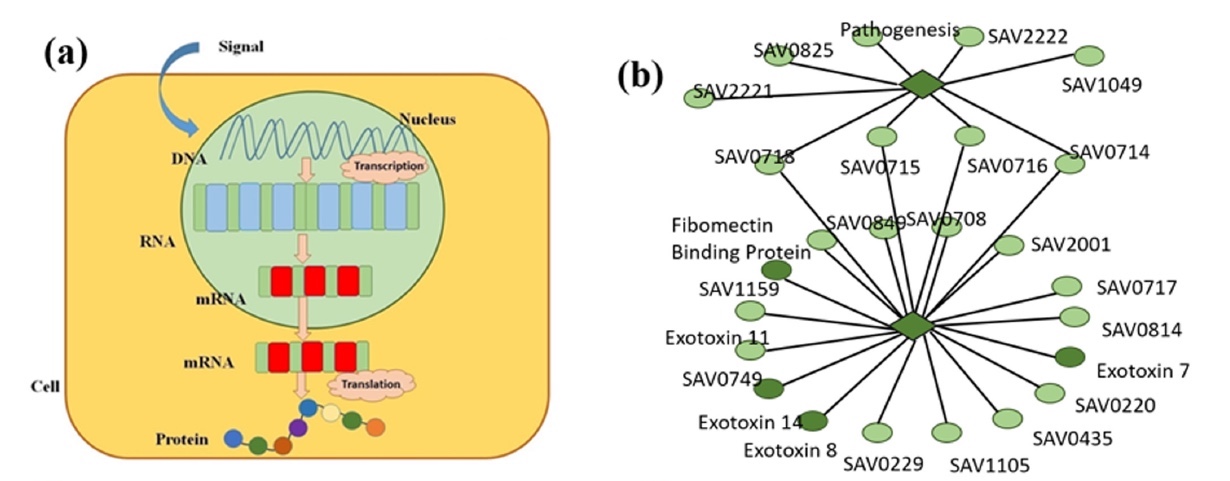
当基因的遗传信息转化为功能性产物时，我们体内最重要的过程之一就是基因表达（图
1a ）。 换句话说，我们的细胞通过基因表达来控制其结构和功能。 我们的基因是一个数据库，人体所有细胞都从该数据库中获取信息，然后执行所需的功能。 因此，我们的嘴不能长出头发，免疫系统可以抵抗感染，血细胞可以输送氧气等。 所有这些过程正是由于细胞编程以执行特定任务而发生的，而这些任务又可以通过激活特定基因进行蛋白质合成来实现。
图片编号1基因表达的调节指示某些蛋白质必须何时产生，产生多少以及持续多长时间。 因此，对这一过程的研究对于全面了解某些生物控制机制如何发挥作用至关重要。
这个复杂的过程对科学家而言很重要，因为有机会对其进行控制，他们将能够制造出具有清晰功能的某些合成细胞，特别是将癌症药物输送到疾病的“心脏”以进行更有效的治疗。
为了改善这种疾病的治疗方法，有必要更详细地了解遗传学方面。 为此，科学家建议以程序的形式呈现人体，其中基因作为代码行，如果程序出现故障，则可以更改。 为了实现这一点，您必须首先创建基因的数学模型。 目前，这样的模型已经存在，但是由于它们旨在研究基因网络中的动力学，因此无法代表。 在同一研究中，应用分形的概念，科学家决定专注于特定基因的表达过程，然后应用基因
FT *对之间的互相关（
1b ）。
转录因子（FT）*是一种mRNA合成控制蛋白，通过连接到特定的DNA位点，包含有关DNA基质上蛋白质一级结构的信息。
简而言之，科学家决定深入研究，而不是考察整个“墙”，而是考察单个“砖”。
研究成果这项研究的对象是真菌酿酒酵母（面包酵母）和细菌大肠杆菌（Escherichia coli）。
通过分析实验对象的基因表达的统计数据，计算出
赫斯特系数* 。
赫斯特系数*是时间序列分析的量度。
时间序列* -在不同时间间隔收集有关指标的一组统计数据。
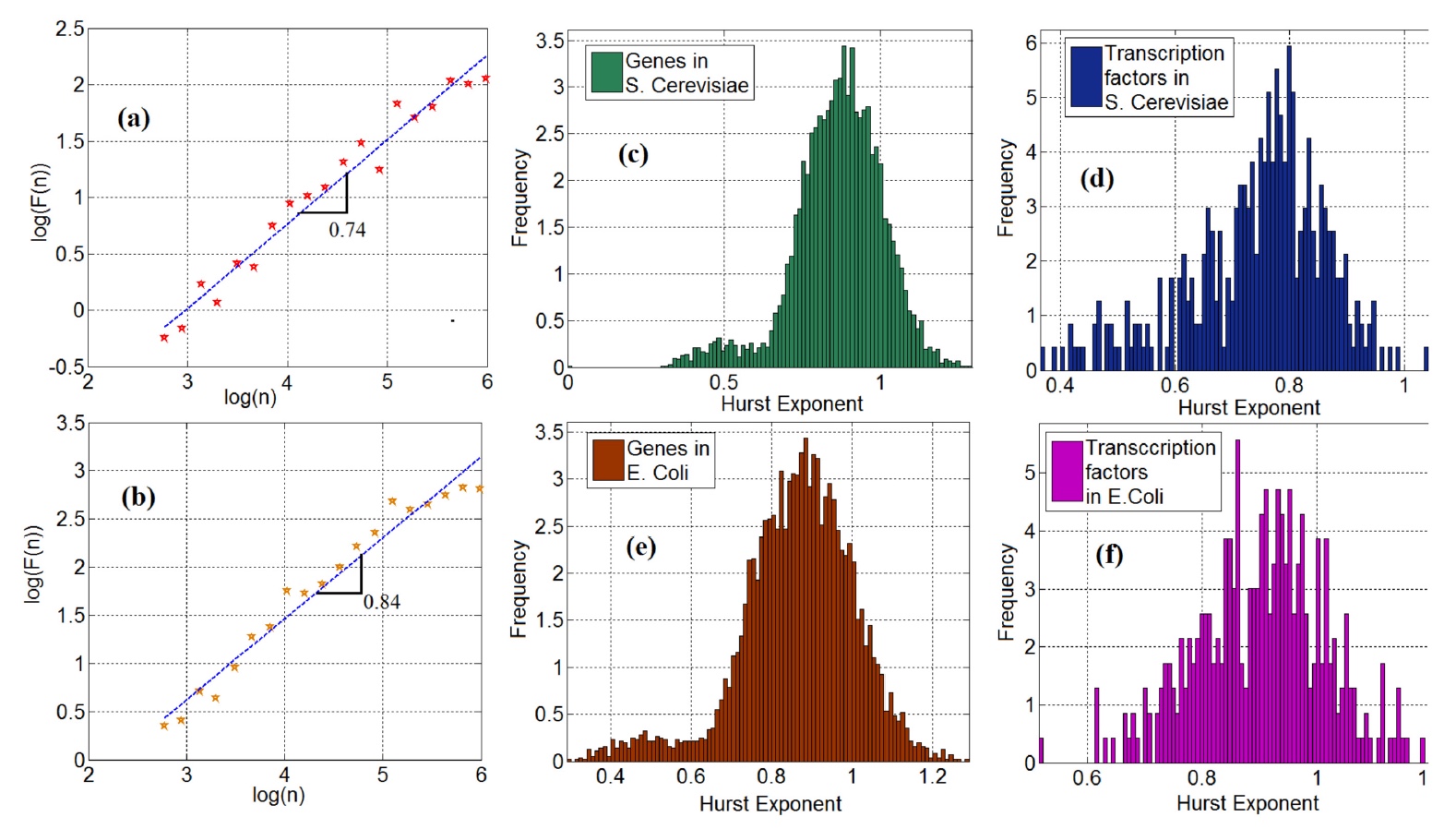图片编号2图 2a （酵母）和
2b （大肠杆菌）显示
了波动的
双对数图*与FT时间序列的尺度有关。
双对数图*是在两个轴（垂直和水平）上使用对数标度的二维数据图。
这些图中曲线的斜率对应于赫斯特系数。 值得注意的是，时间序列的基因中有95％（酵母）和98％（杆菌）显示出
长期依赖性* 。
长期依赖性* -时间序列分析中的一个指标，指示两个点的统计依赖性的缓慢衰减，并且两个点之间的时间间隔增加。 它由赫斯特系数指标-从0到1确定。如果指标高于0.5，则我们有很强的长期关系，低于0.5-产生相反的效果。
在这种特殊情况下，长期依赖的赫斯特系数为0.5，这从理论上表明它不存在。 但是，对数据的进一步分析表明，该指标超过了0.5的值，这表明在基因表达中存在时间序列的长期依赖性（
2c和
2e ）。 这表明基因-FT的时间序列不能被认为是随机的，因此当存在一系列事件时，它们应该基于马尔可夫链进行建模，每个事件的随机性仅取决于前一个事件。
像基因一样，转录因子也显示出长期关系：酵母和芽孢杆菌的转录因子为97％（图
2d和
2f ）。
现在将少量的分形分析添加到普通碗中。 首先，科学家提请我们注意赫斯特系数分布的双峰性。 最好在图
2c和2e中看到。 科学家通过以下事实解释了这一观察结果：基因表达中存在扩散过程，具有多种扩散潜能。 因此，双峰可以用具有不同电势的非平衡布朗运动来解释。 但是，这种说法还需要其他证据，科学家将在随后的研究中寻找这些证据。
现在我们将回到多重分形。 科学家使用趋势变化的多重分形分析来确定基因表达时间序列中多重分形特征的存在与否。 该分析表明基因和FT均存在。
鉴于实验时间序列的长度有限，科学家们还应用了
bootstrap *方法来准确确定（更精确地确定）长期依赖性的存在。
Bootstrap * -一种用于分析概率分布统计信息的技术。
对于基因表达的每个时间序列，准备了10个随机子间隔，每个子间隔包含初始时间序列的90％有序片段。 此外，对于所有选项，都计算了赫斯特系数。 因此，获得了实验时间序列指标和随机版本指标之间的差异。 对于大肠杆菌，差异仅为0.006％，而对于面包酵母，差异甚至更小-0.0001％。 因此，证实了两个样品中都存在长期依赖性。
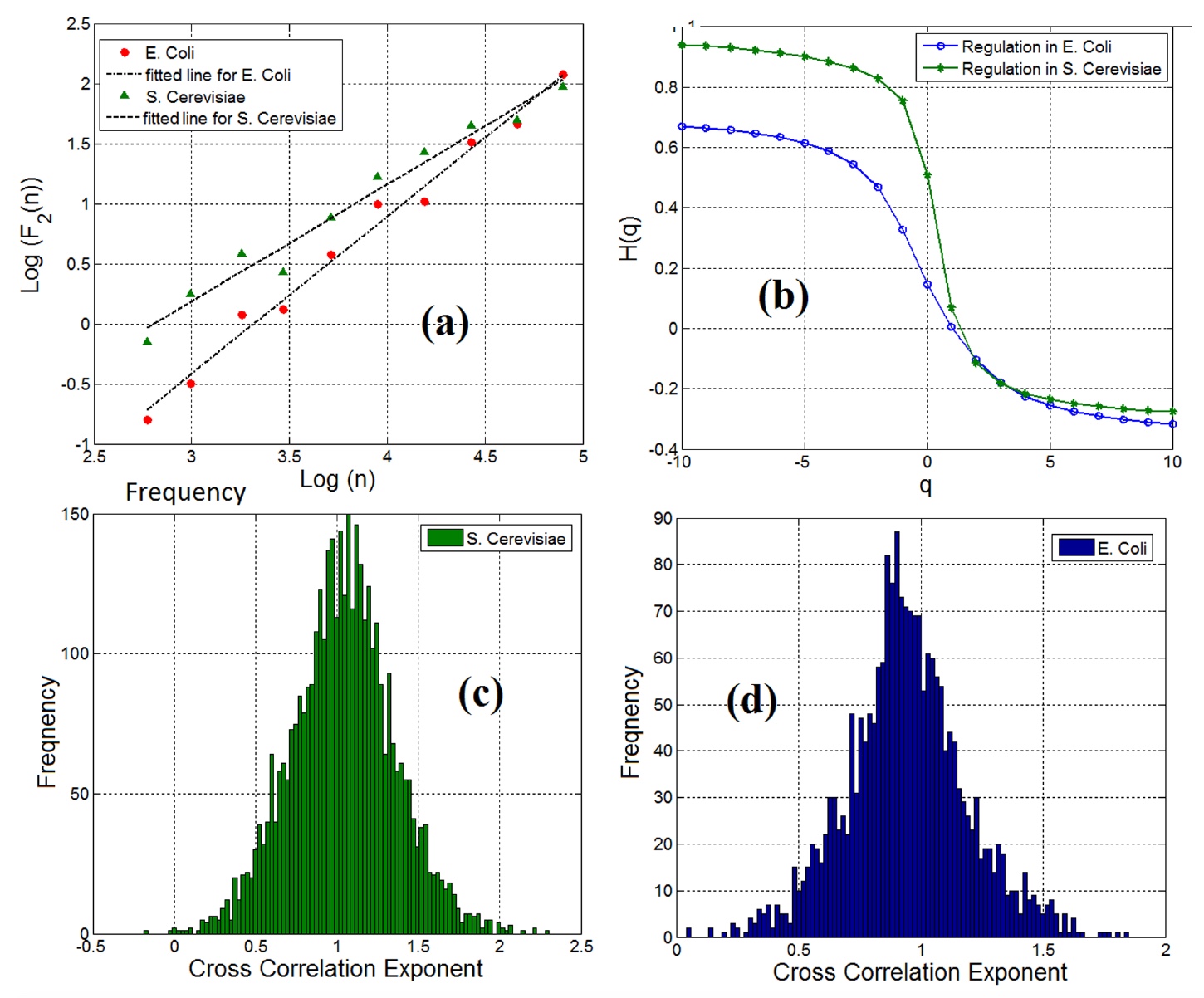
在分别考虑了感兴趣的基因和FT的特征后，科学家们开始着手分析基因FT对作为单个对象。 互相关指数的计算表明，在两个样本中，有98％的基因-FT对具有长期依赖的特性（
3a ）。
图片编号3趋势波动的多重分形分析证实了基因-FT对中多重分形特征的存在（图
3b ）。
值得注意的是，无论在基因调控网络中在成对的基因和转录因子中都观察到分形和长期互相关的事实，互相关都不是对的。 图
3c （酵母）和
3d （大肠杆菌）显示了基因-FT对的互相关。
科学家利用这些图来测量信息熵，从而测量各种细胞类型的基因调控网络的信息含量，以定量分析和规范基因调控网络，熵指标为：4.18-酵母菌，5.29-大肠杆菌。 这表明面包酵母中的基因表达网络要比大肠杆菌中的基因表达网络大得多，并且显示出更复杂的动力学。
现在最有趣的是建立数学模型。 科学家选择了该模型的两个版本：Mandelbrot集和小波二叉树形式的集。
利用先前获得的分形谱中霍尔德系数的指标，科学家们发现，使用Mandelbrot集可以对面包酵母基因调控网络中所有基因FT中只有0.04对进行建模。 在大肠杆菌中，无法通过这种方法对任何一对进行建模。
如果我们考虑那些能够模拟的对，那么模型和实验观察之间的数据会有很大的差异。 结论是，由于Mandelbrot集而导致的建模方法不合适。
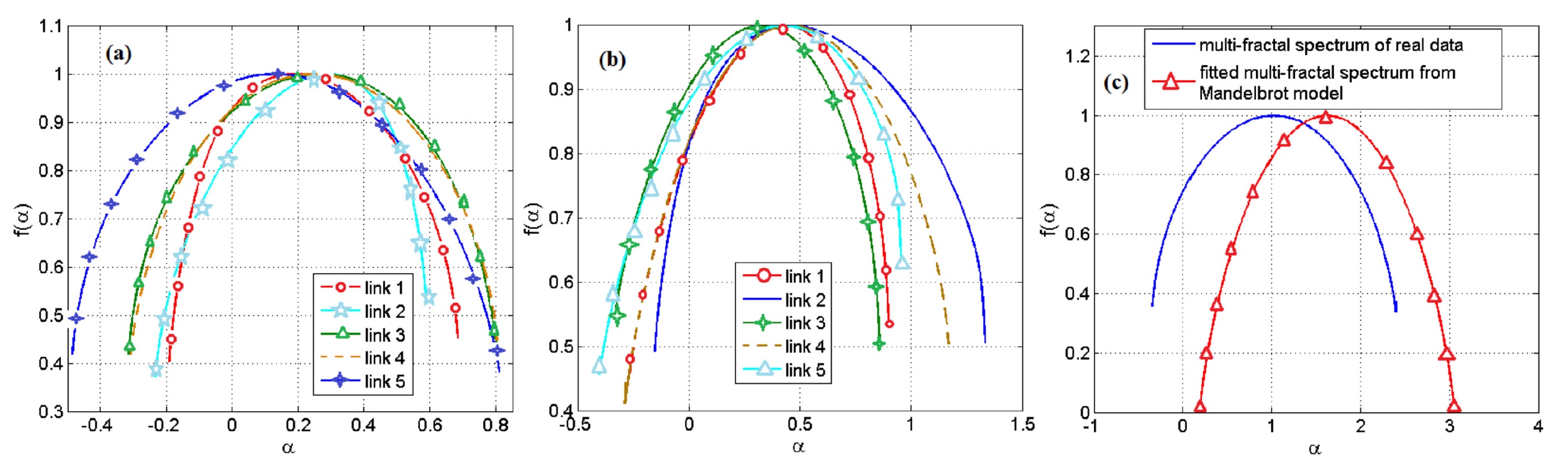图片编号4上图中显示了使用基于Mandelbrot集的模型的结果。 最亮的是
4c ，在这里我们可以看到数据之间的差异。
科学家们还比较了在基因调控网络中观察到的相互依赖性的多重性和在小波二叉树上的随机级联的多重分形模型。
研究人员决定检查W级联的对数模型是否适合于基因调控网络中的基因FT对表示。 根据经验谱和奇异谱，计算了该模型的参数。 接下来，对计算出的和经验的多重分形谱的相交区域进行计算，其比例成为接受或拒绝该数学多重分形模型的主要标准。
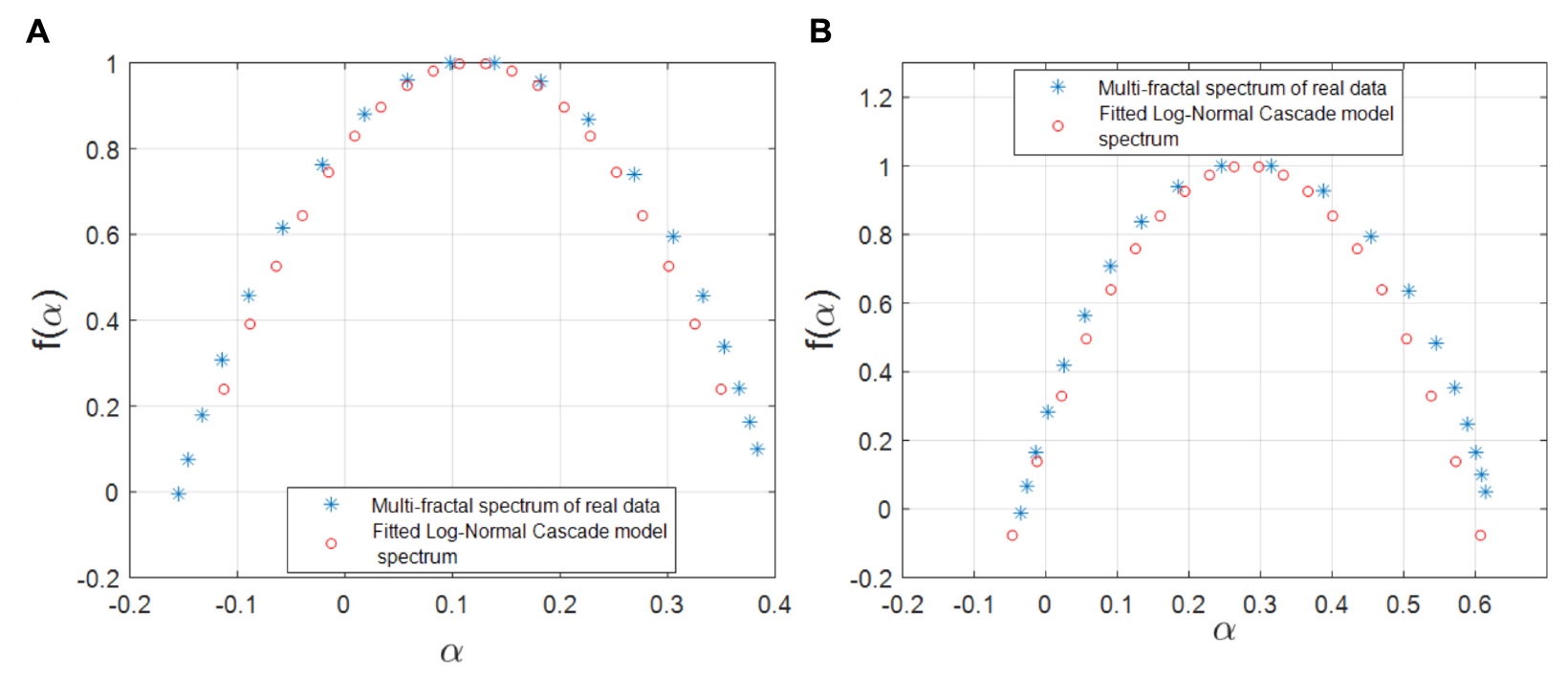图片编号5从上面的图表可以看出，该模型演示了模拟和经验的多重分形光谱，几乎与先前进行的观测和计算数据完全相关。
要更详尽地了解这项研究的细微差别，建议您在
此链接上查看研究小组的报告。
结语这项研究主要是理论性的，因此具有很大的实际应用潜力，因为它有助于对调节基因表达的网络进行数学建模，这是任何活生物体中最重要的过程之一。 无论听起来多么奇怪，都很难理解复杂的过程。 为了简化任务，有必要将流程分为各个组件，绘制其“地图”，并遵循所需的路线，并注意所有重要的特征和特性。 数学建模，别无其他，对此非常有用。 在研究了对象或过程的数学模型之后，我们可以在继续研究实际的对象或过程之前先了解正在处理的内容。
这项研究再次证实，不仅物理学和化学统治着世界，而且数学距离科学奥林匹亚的最后位置还很遥远。
谢谢大家的关注，保持好奇心，祝您工作愉快。
感谢您与我们在一起。 你喜欢我们的文章吗？ 想看更多有趣的资料吗？ 通过下订单或将其推荐给您的朋友来支持我们，
为我们为您发明的入门级服务器的独特模拟，为Habr用户提供
30％的折扣： 关于VPS（KVM）E5-2650 v4（6核）的全部真相10GB DDR4 240GB SSD 1Gbps从$ 20还是如何划分服务器？ （RAID1和RAID10提供选件，最多24个内核和最大40GB DDR4）。
VPS（KVM）E5-2650 v4（6核）10GB DDR4 240GB SSD 1Gbps至1月1日免费，如果您支付六个月的费用，则可以
在此处订购。
戴尔R730xd便宜2倍？ 仅
在荷兰和美国，我们有
2台Intel Dodeca-Core Xeon E5-2650v4 128GB DDR4 6x480GB SSD 1Gbps 100电视（249美元起） ！ 阅读有关
如何构建基础架构大厦的信息。 使用价格为9000欧元的Dell R730xd E5-2650 v4服务器的上等课程？