深度精度清晰

深度精度是任何图形程序员迟早都要面对的难题。 关于这个主题已经写了很多文章和作品。 在不同的游戏和引擎以及不同的平台上，您可以看到深度缓冲区的许多不同格式和设置。

GPU上的深度转换似乎并不明显，因为它如何与透视投影相互作用，并且对等式的研究并未阐明这种情况。 要了解其工作原理，请绘制一些图片很有用。



本文分为三个部分：

1. 我将尝试解释非线性深度转换的动机。
2. 我将展示一些图表，这些图表将帮助您直观地和直观地了解非线性深度转换在不同情况下的工作方式。
3. 讨论了加强透视图渲染的精度的主要发现[Paul Upchurch，Mathieu Desbrun（2012）]关于舍入浮点误差对深度精度的影响。

为什么1 / z？

硬件GPU 深度缓冲区通常不存储对象与相机之间距离的线性表示，这与第一次会议上天真地期望的相反。 而是，深度缓冲区存储与视图空间深度成反比的值。 我想简要描述做出这一决定的动机。

在本文中，我将使用d表示深度缓冲区中存储的值（DirectX的范围为[0，1]），使用z表示深度视图空间，即 距相机的实际距离，以世界单位为单位，例如米。 通常，它们之间的关系具有以下形式：



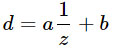
其中， a，b是与飞机的近距和远距设置相关的常数。 换句话说， d总是从1 / z开始的线性变换。

乍看起来， z的任何函数都可以视为d 。 那她为什么看起来那样呢？ 这样做的主要原因有两个。

首先， 1 / z自然适合透视投影。 这是最基本的变换类，可以保证保留直线。 因此，透视投影适用于硬件光栅化，因为三角形的直边在屏幕上保持笔直。 我们可以利用GPU已经执行的透视除法从1 / z进行线性变换：



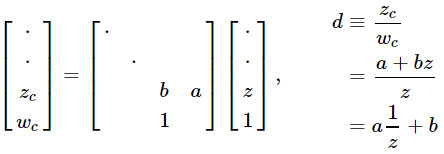
当然，这种方法的真正优势在于可以将投影矩阵与其他矩阵相乘，从而使您可以将许多变换组合为一个。

第二个原因是， 如Emil Persson所述 ， 1 / z在屏幕空间中是线性的。 这使得在栅格化过程中易于将d插值到三角形中，以及诸如分层Z缓冲区 ， 早期Z消隐和压缩深度缓冲区之类的东西 。

深度图

方程很复杂，让我们看几张图片！



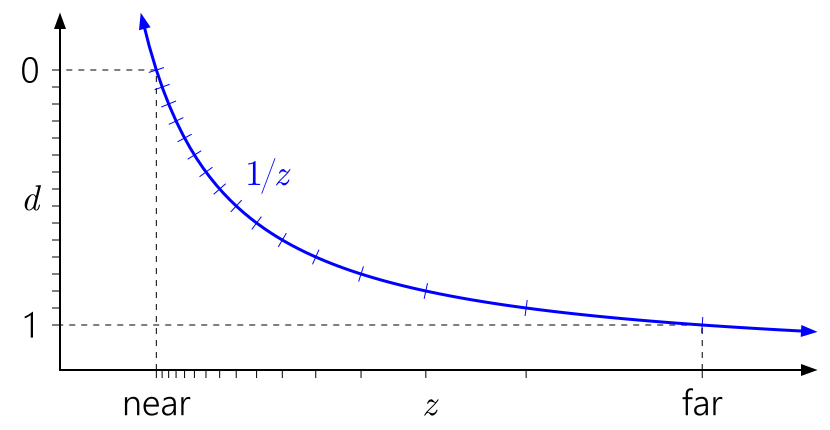
读取这些图表的方法是从左到右，然后从下到下。 从左轴上的d开始。 由于d可以是从1 / z开始的任意线性变换，因此我们可以将0和1布置在轴上的任何方便位置。 标记表示不同的深度缓冲区值。 为了清楚起见，我对4位整数归一化深度缓冲区建模，因此有16个均匀间隔的标记。

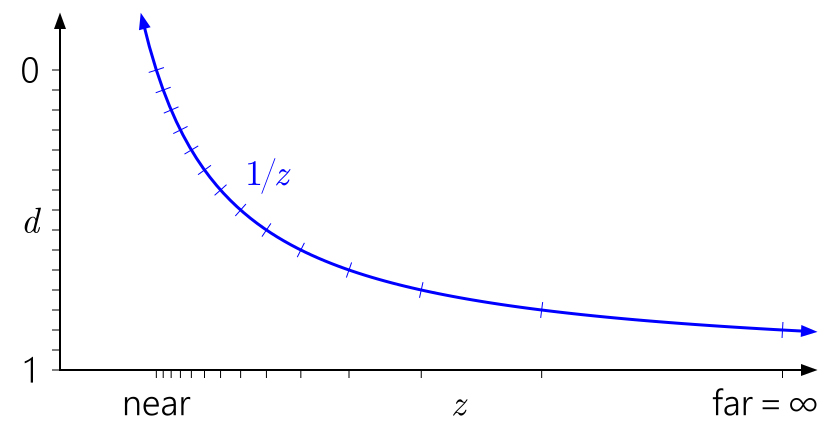
上图显示了“标准”香草深度到D3D和类似API的转换。 您会立即注意到，由于1 / z曲线，如何将接近近平面的值进行分组，以及如何分散接近远平面的值。

也很容易理解，为什么在平面附近对深度精度影响如此之大。 靠近平面的距离将导致d的值相对于z的值快速增加，这将导致值的分布更加不均匀：



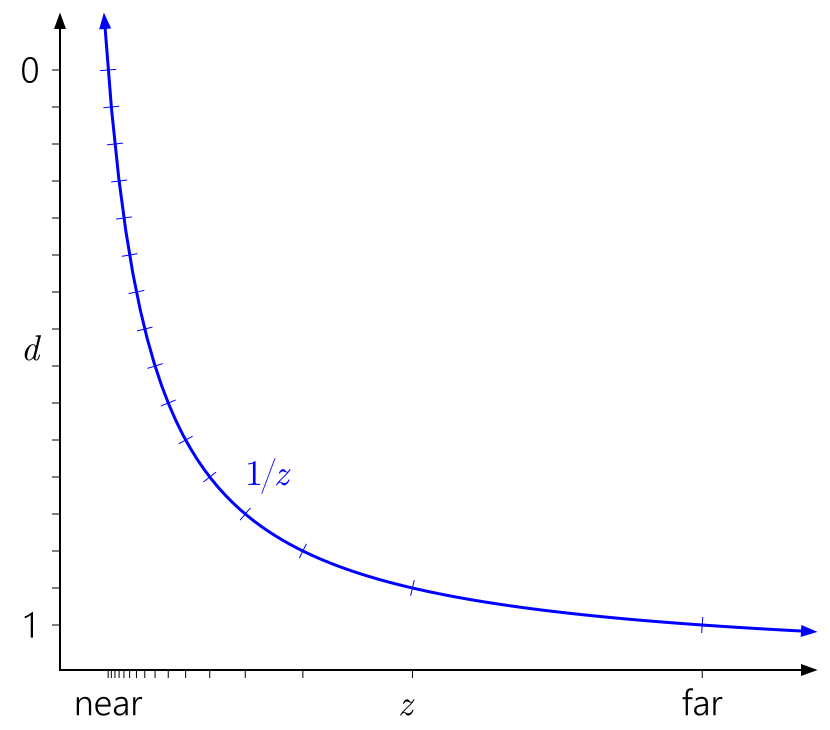
同样，在这种情况下，很容易看出为什么将远平面移动到无穷大并没有那么大的影响。 这只是意味着将d的范围扩大到1 / z = 0 ：



但是浮点深度呢？ 下图已添加了与浮点格式相对应的标记，其中指数为3位，尾数为3位：



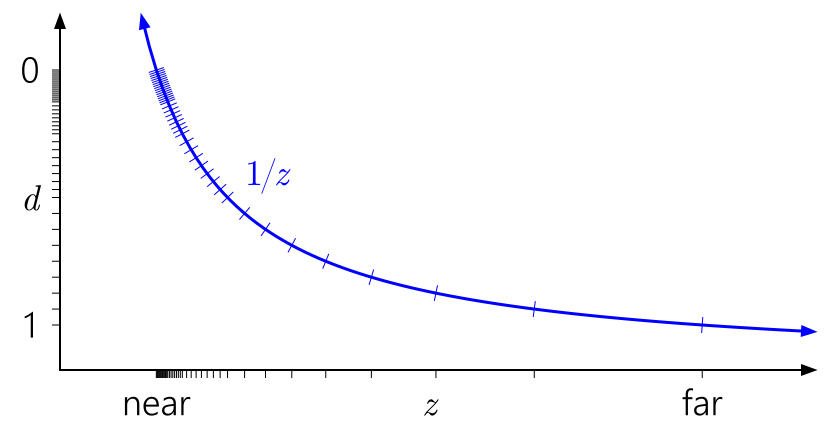
现在，在[0,1]范围内，有40个不同的值-早于16个值，但是其中大多数都在靠近近平面的情况下被无用地分组（更接近0的浮点数具有较高的精度），而实际上我们并不需要太多精度。

现在一个众所周知的技巧是反转深度，在d = 1上显示近平面，在d = 0上显示远平面：



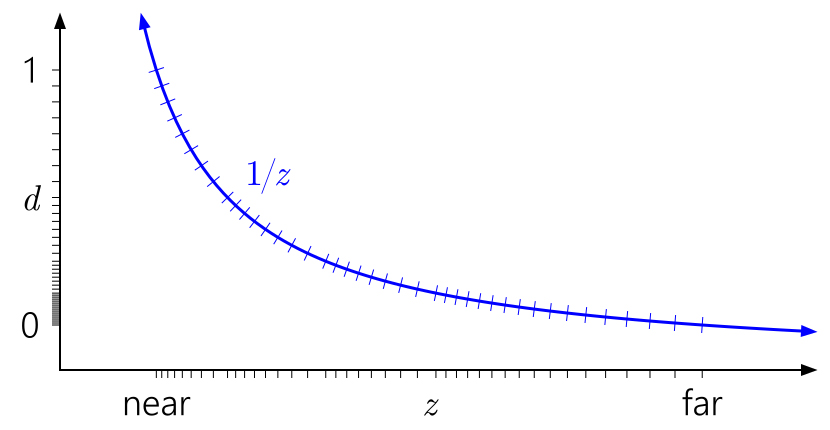
好多了！ 现在浮子的准对数分布以某种方式补偿了1 / z的非线性，而更靠近近平面时，其精度类似于整数深度缓冲区，而在其他地方则明显更高。 如果您距离相机较远，则深度精度会非常缓慢地下降。

反向Z技巧可能已经被独立地重制了好几次，但是至少第一次提到是在SIGGRAPH '99论文中 （Eugene Lapidous和Guofang Jiao（不幸的是不公开））。 最近， Matt Petineo和Brano Kemen在博客上提到了他，并在Emil Persson的演讲中提到了他创建《巨大游戏世界 SIGGRAPH 2012》。

所有先前的图形都假定投影后的深度范围为[0.1]，这是D3D中的惯例。 OpenGL呢？



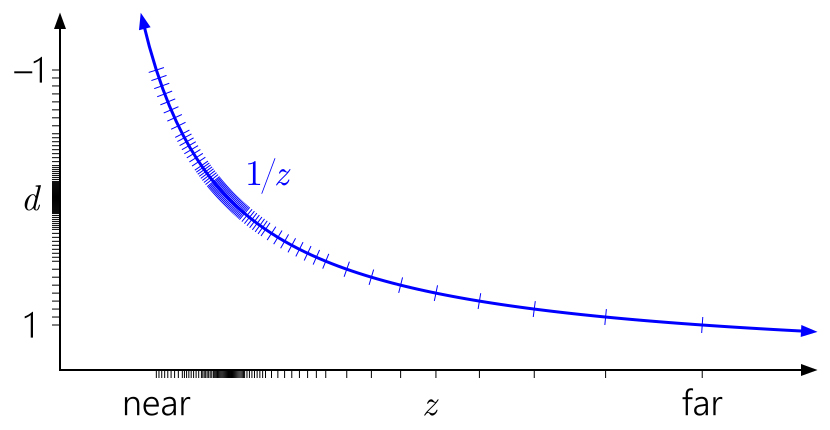OpenGL默认情况下假设投影后的深度范围为[-1，1]。 对于整数格式，没有任何变化，但是对于浮点，所有精度都集中在中间，毫无用处。 （将深度值映射到范围[0,1]，以便以后存储在深度缓冲区中，但这无济于事，因为到[-1,1]的初始映射已经破坏了该范围的一半的所有精度。）而且由于对称性，这种技巧反向Z在这里不起作用。

幸运的是，在桌面OpenGL中，可以使用广泛支持的扩展名ARB_clip_control （也从OpenGL 4.5开始， glClipControl是标准的 ）来解决此问题。 不幸的是，GL ES正在生产中。

舍入误差的影响

1 / z转换以及float与int深度缓冲区的选择是精度的重要组成部分，但并非全部。 即使您具有足够的深度精度来表示要尝试渲染的场景，也很容易在顶点转换过程中因算术错误而降低精度。

在本文开头，提到Upchurch和Desbrun研究了这个问题。 他们提出了两个主要建议以最大程度地减少舍入误差：

1. 使用无限远的平面。
2. 保持投影矩阵与其他矩阵分离，并在顶点着色器中将其作为单独的操作应用，而不是与视图矩阵结合使用。

Upchurch和Desbrun使用一种分析方法提出了这些建议，该方法基于将舍入误差作为每个算术运算中出现的小随机误差进行处理，并在转换过程中将它们跟踪到一阶。 我决定在实践中测试结果。

这里的源是Python 3.4和numpy。 该程序的工作方式如下：生成一系列随机点，按深度排序，在近平面和远平面之间线性或对数定位。 然后，将这些点与矩阵的视图和投影相乘，并使用32位浮点数进行透视除法，并且可选地，将最终结果转换为24位int。 最后，它遍历序列并计算2个相邻点（最初具有不同的深度）变得相同的次数，因为它们具有相同的深度或顺序完全改变。 换句话说，该程序在各种情况下测量发生深度比较错误的频率，该频率对应于诸如Z战等问题。

这是近= 0.1，远= 10K，线性深度为10K的结果。 （我尝试了对数深度间隔和其他近/远比率，尽管具体数字有所不同，但结果的总体趋势是相同的。）

在表中，“ eq”（深度最接近的两个点）在深度缓冲区中获得相同的值，“ swap”（交换）-深度最接近的两个点被交换。

	复合视图投影矩阵		独立的视图和投影矩阵
	float32	int24	float32	int24
不变的Z值（对照测试）	0％当量 0％掉期	0％当量 0％掉期	0％当量 0％掉期	0％当量 0％掉期
标准投影	45％当量 18％掉期	45％当量 18％掉期	当量77％ 0％掉期	当量77％ 0％掉期
无限远	45％当量 18％掉期	45％当量 18％掉期	当量76％ 0％掉期	当量76％ 0％掉期
反转z	0％当量 0％掉期	当量76％ 0％掉期	0％当量 0％掉期	当量76％ 0％掉期
无限+反向Z	0％当量 0％掉期	当量76％ 0％掉期	0％当量 0％掉期	当量76％ 0％掉期
标准+ GL风格	eq的56％ 12％掉期	eq的56％ 12％掉期	当量77％ 0％掉期	当量77％ 0％掉期
无限+ GL风格	当量59％ 10％掉期	当量59％ 10％掉期	当量77％ 0％掉期	当量77％ 0％掉期

对于没有图的事实，我深感抱歉，因为这里没有足够的尺寸，无法建立尺寸！ 无论如何，看一下这些数字，显而易见的是以下结论：

• 在大多数情况下， int和float depth buffer之间没有区别。 用于计算深度的算术错误会覆盖转换为int时的错误。 部分原因是float32和int24具有几乎等于[0.5.1]的ULP（精度最低的单位是到最近的相邻数字的距离）（因为float32具有23位尾数），所以转换误差几乎没有添加到整个深度范围内int。
• 在大多数情况下， 视图矩阵和投影矩阵的分离（遵循Upchurch和Desbrun的建议）可以改善结果。 尽管总错误率并未降低，但“掉期”变为相等的值，这是朝正确方向迈出的一步。
• 无限远平面会稍微改变错误的频率。 Upchurch和Desbrun预测数值错误（准确度错误）的频率将减少25％，但这似乎并未导致比较错误的频率减少。

但是，与魔术反Z相比，上述发现并不真实。 检查：

• 带浮点深度缓冲区的反向Z在测试中给出零错误率 。 现在，如果继续增加输入深度值的间隔，您当然会遇到一些错误。 但是，带浮点的反向Z比任何其他选项都更准确。
• 具有整数深度缓冲区的反向Z与其他整数选项一样好。
• 反向Z模糊了复合视图和单独的视图/投影矩阵以及有限和无限远平面之间的区别。 换句话说，使用反向Z可以将投影与其他矩阵相乘，并使用所需的任何远平面，而不会影响精度。

结论

我认为结论很明确。 在任何情况下，处理透视投影时，只需使用浮动深度缓冲区和反向Z即可 ！ 并且，如果无法使用浮动深度缓冲区，则仍应使用反向Z。 这并不是解决所有疾病的灵丹妙药，尤其是当您创建具有极端深度范围的开放世界环境时。 但这是一个很好的开始。