
哈Ha! 我叫Akhmadeev Rinat,我叫Sr。 PHP开发人员。
我将向您提供报告摘要。 再次设置密码! 如何使用HighLoad ++ 2018击败Virgil Security的Alexey Ermishkin克服暴力行为并使黑客一无所获 。
当我去看报告时,我感到悲观。 但是因为 由于是Virgil Security,我还是决定去。 一开始,该报告似乎是队长,我什至开始失去兴趣,但是后来,事实证明,我什至发现了几种新的密码保护方法,而不是通常的盐散列。
该报告讨论了保护密码免受哈希攻击的方法,并采用了更现代的方法,例如Facebook的密码Onion,Sphinx和Pythia。 最后,引入了新的简单密码强化加密服务(PHE)。
我非常喜欢这份报告,以致编写了纲要。 我建议大家熟悉一下自己。
Alexey Ermishkin在评论中分享了幻灯片和视频报告:
摘要
参赛作品

大家好,大家早上好! 我很高兴在高负载会议上与大家见面。 我叫Alexey Ermishkin,我在Virgil Security工作。

我们致力于为个人开发人员和企业开发各种加密产品。 我们专注于端到端解决方案,这是当您不需要信任服务即可执行任何操作(例如数据传输,身份验证等)时。 我们的SDK是开放的,所有人均可使用。
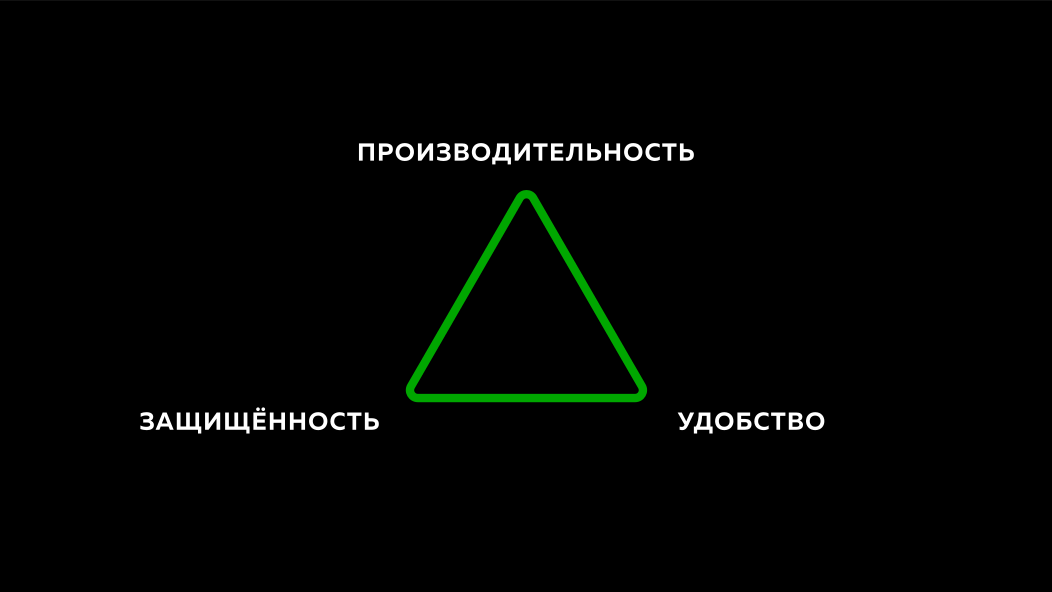
长期以来,密码一直被用作身份验证的手段,也可以用作进入某处的一种方式。 那是很久以前计算机出现的。 但是随着计算机的出现,IT系统的出现,人们并没有放弃使用密码的习惯。 对于开发人员而言,这成为一个很大的问题,因为他们遇到了如何使系统既方便又快速且安全的问题。 很多时候,当其中两个方面都想做得很好时,第三个方面的效果就不太好。 如果您使系统高效且安全,则可能会带来不便,等等。

那么,我们今天要谈什么呢?
我将讨论防止离线攻击的方法。 当密码进入您的数据库时,则用户将无法控制它们。 如果您的数据库被黑客入侵,它将在某个地方泄漏,然后黑客可以对其进行任何处理。 即使您以某种方式保护了密码,它们也可以开始对它们进行排序,并且它们不需要为此与任何人进行交互,他们已经拥有了一切。 此外,用户不会停止使用弱密码。 密码策略当然是有用的东西,但也不总是很方便,即 当甚至有人输入似乎很强的密码时,该政策仍然指出您需要添加字母或数字,这对他们来说并不方便。 同样显而易见的是,问题在于需要将用户输入的内容与数据库中的内容进行比较。 如何安全地做到这一点? 好吧,我们不要忘记,公司内部还有一些人并不完全友好,他们也想保护自己不受他们侵害。
散列
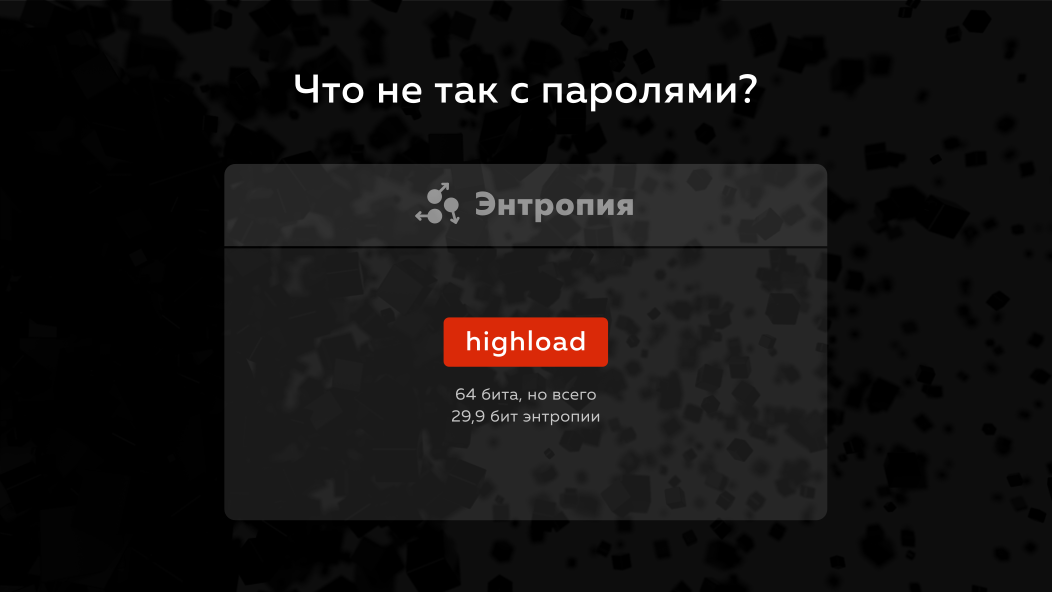
原则上,为什么密码这么麻烦,为什么值得更仔细地使用它们呢? 问题在于密码的熵很小。 什么是熵? 这是数据中包含的信息量,即 例如,在高负载单词中,8个字母为8个字节,但是如果我们计算熵,它将不会像整个单词一样为64位,而是少于30位。 今天,当他们谈论破坏密码时,他们说有可能在不超过或不少于几位的时间内用熵破解密码。 即 即使密码的数量也没有考虑在内。

人们是如何开始使用密码安全性的? 我想到的第一件事是使用单向加密哈希 。

它们的显着特征是它们不能后退。 即 如果您将某些信息传输到此哈希,并在输出中收到一个值,则无法从该值取回该信息。 但是,不幸的是,它们很快被计算出来。 例如,一个由4个NVidia图形卡组成的现代化集群可以每秒处理数十亿个密码。 即 如果密码的熵小于40位,那么一簇4个视频卡将在一分钟或更短的时间内将其拾取。
彩虹桌

此外,每个棘手的哈希表都有自己的Rainbow表 。 这张桌子是什么,它们是怎么制成的?

即 他们采用适合硬盘驱动器的最流行的密码和字符组合,为它们考虑散列,然后将它们放在更多的存储空间中,存储容量达到数TB。 当存在某种哈希时,您无法计算它,但可以从这些表中很快找到它,并将其与先前计算的密码进行比较。 即 表的优点是它们可以非常快速地工作,但是您需要大量空间来存储它们。 尽管如此,Internet上仍然有一些表格,它们是最流行的哈希表,可以下载甚至购买。
提要的作者注意: 维基百科与发言者不同意:“彩虹表是搜索表的特殊版本,用于通过合理地折衷表中的搜索时间和所占用的内存的机制来反转密码哈希函数。” 即 它不会存储磁盘上最流行的密码的哈希值,而只是简单地存储某些密码的哈希值,其余密码是根据存在的密码来计算的-表中的每条记录都有多个密码。
盐

但是话又说回来,每个彩虹桌子都有自己的盐 。 什么是盐? 这是一个随机字节组,附加在密码后面。 它存储在哈希表附近的某个表中,并且可以防止彩虹表。

即 将手放在含盐哈希值的基础上的人仍然必须计算这些哈希值。 但是问题在于这些哈希值的计算速度非常快,而盐在这里并没有太大帮助。
如何减慢搜索速度?

一种自然的解决方法是以某种方式减慢哈希排序。 怎么办呢?

最幼稚的方法是我们采用某种哈希函数(例如sha256),并对其进行迭代计算,即 计算哈希值,再根据此哈希值计算哈希值,等等。 您可以执行数千次甚至数百万次。 问题是,如果您自己编写这样的实现,那么它很可能会比专门从事密码猜测的人员的实现慢。

SCrypt , Bcrypt , Argon2
因此,密码学家想出了几种专门设计用于减慢密码搜索速度的功能-他们使用大量的内存和所有可能的现代处理器指令。 如果受此功能保护的密码落入攻击者的手中,那么他们将不得不使用功能非常强大的硬件。

例如,最现代的Argon2函数的工作方式如下:在该图中,您可以看到有许多不同的内存块可用于运行哈希。 他以各种方式往返执行此操作,内存使用非常密集,整个内存都被使用。 优化这样的功能(搜索速度)相当困难。

但是这些方法也有其缺点。 这些功能特别慢,但不仅对攻击者特别慢,对您也特别慢。 他们会装你的铁。 这些功能是可自定义的,即 您可以选择要使用多少内存来计算单个密码的哈希值(最多几GB)以及该内存上的通过次数。 如果您非常认真地设置这些参数,那么您自己的硬件将受到损害,并且如果您有很多人登录系统,则只需要分配相当大的资源来保护密码和简单密码,那么,仍然可以选择非常简单的密码。
Facebook的密码洋葱

人们对此进行了思考,并提出了一个问题:是否可以在不加载后端,不加载自己的服务器的情况下实现相同的属性?

Facebook的先驱者之一。 您所看到的这些行是Facebook的历史阶段,它们如何保护密码,起初它们只是密码,然后他们采用了已经破解了很长时间的旧md5函数,然后在其中添加了盐并进行了sha1哈希处理,然后它发生了有趣的是,他们将hmac函数(这是带有密钥的哈希)的计算带到了远程服务。
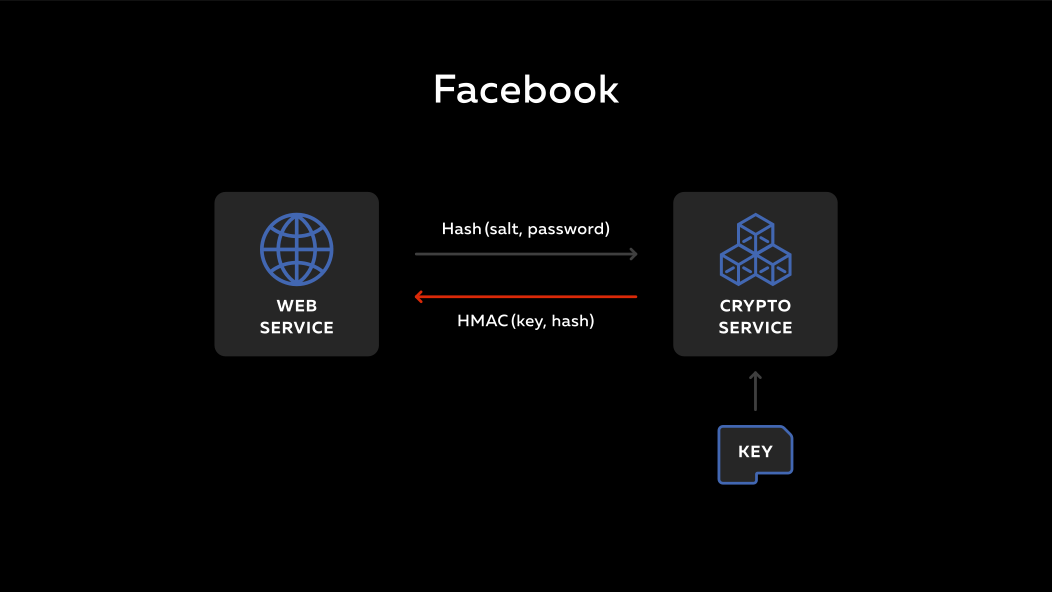
如何运作? 有一个后端,有一个远程服务。 此服务上有某种秘密密钥。 一个人进入后端,输入他的密码。 此密码与数据库中的salt混合在一起,通过哈希运行并发送到服务。 该服务获取其私钥,计算hmac函数,然后将其全部发送回去。 在后端,它放在基础中。
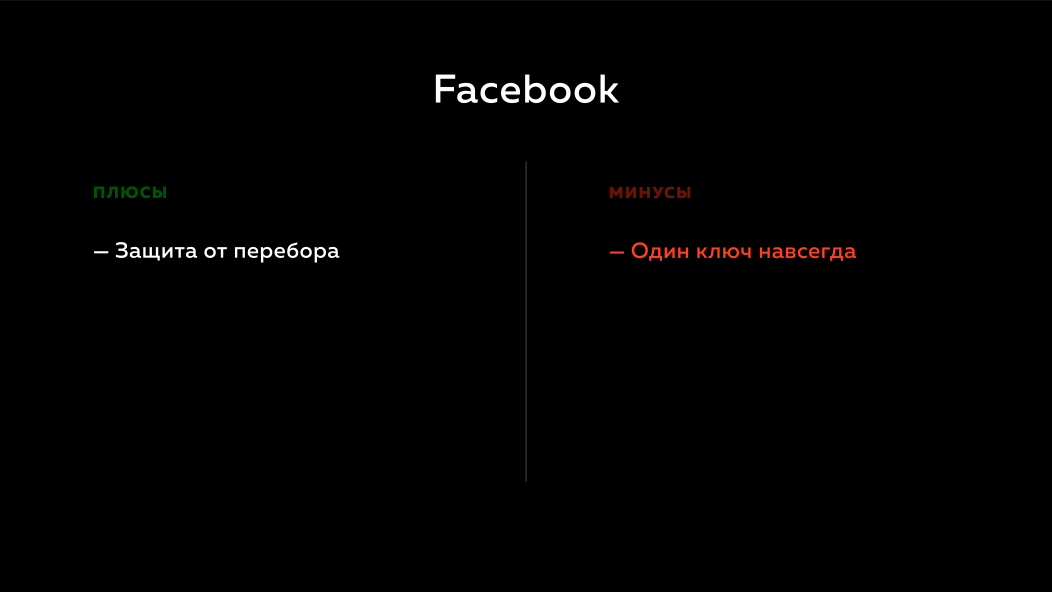
它有什么作用? 如果Facebook有用户数据库,则不值得在其中对密码进行排序,因为它们没有远程密钥。 但是Facebook的方法的问题在于,如果他们的远程私钥出了点问题,那么他们将陷入大麻烦。 他们对此无能为力,因为他们使用哈希,使用hmac。 他们无法以某种方式解决这种情况,以便用户不会注意到任何东西,这将使自己陷入困境。
狮身人面像
密码学家研究了整个过程。 他们喜欢使用远程服务的想法,并决定思考:是否有可能做得更好? 是否有可能建立一个类似的系统,但没有Facebook赋予它的缺点?

他们决定按以下方式解决此问题:如果密码或密码哈希表示为数字怎么办? 如果我们有单词passw0rd ,则它由8个字节组成。 在几乎所有的编程语言中,都有八字节的整数类型,即 原则上,这是相同的。 即 8个字节,单词passw0rd ,我们可以将其表示为常规十进制数。 这给了我们什么? 这给了我们完全不同的行动自由。 我们可以从中添加密码或哈希,将它们相乘,然后将其转换为其他数字。 我们可以对它们执行真正的数学运算。

Sphinx是最早使用此技术的系统之一。 她是几年前出现的。 这是确定性的密码管理器。 有很多不同的程序,例如keepass ,您可以在其中拥有一个主密码,并且它会为每个站点随机生成一个。 但是,在确定性的内容中,您可以输入主密码,要访问的站点,并在那里计算内容并为每个站点颁发唯一的密码。 但是很明显,如果此主密码出入某个地方,那么您网站上的所有密码都会遭到永久破坏。
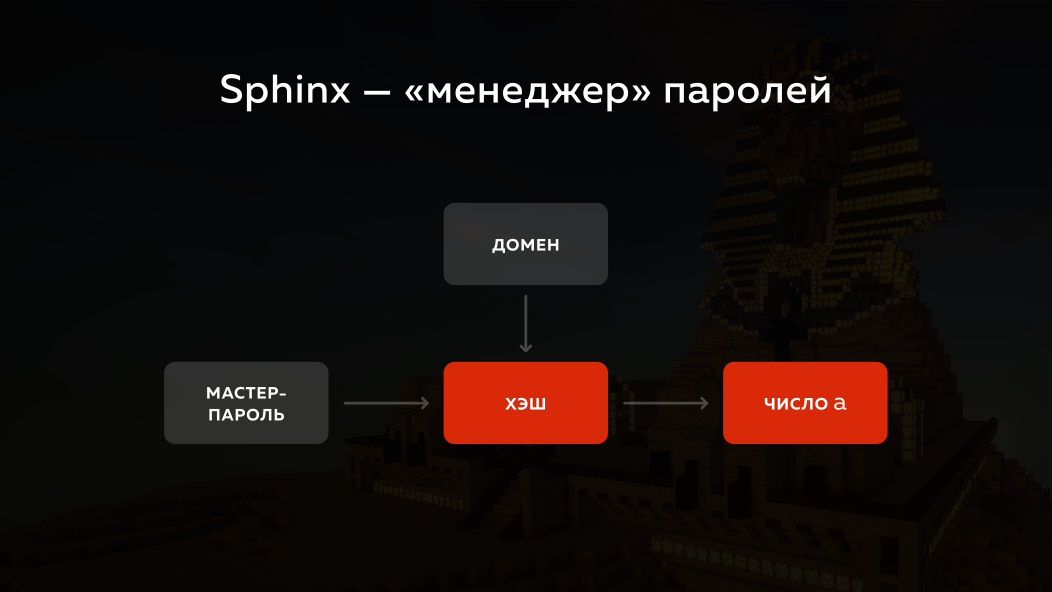
Sphinx如何解决这个问题? 他获取主密码,获取您要登录的域,通过哈希将整个内容运行起来并将其转换为数字。 但实际上,这里使用的是椭圆密码学,为简单起见,我将使用普通的数学方法对所有普通数字进行解释。 他把它变成一个数字(我们叫a ),接下来他要做什么?

绝对美妙的事情,每一次我们可以生成一个大随机数r 。 如果我们将数字a r的幂,然后稍后再将这个数字r的幂,那么我们又得到了相同的数字a ,对吗? 即 我们可以从一开始就屏蔽某些内容,然后再对其进行屏蔽。
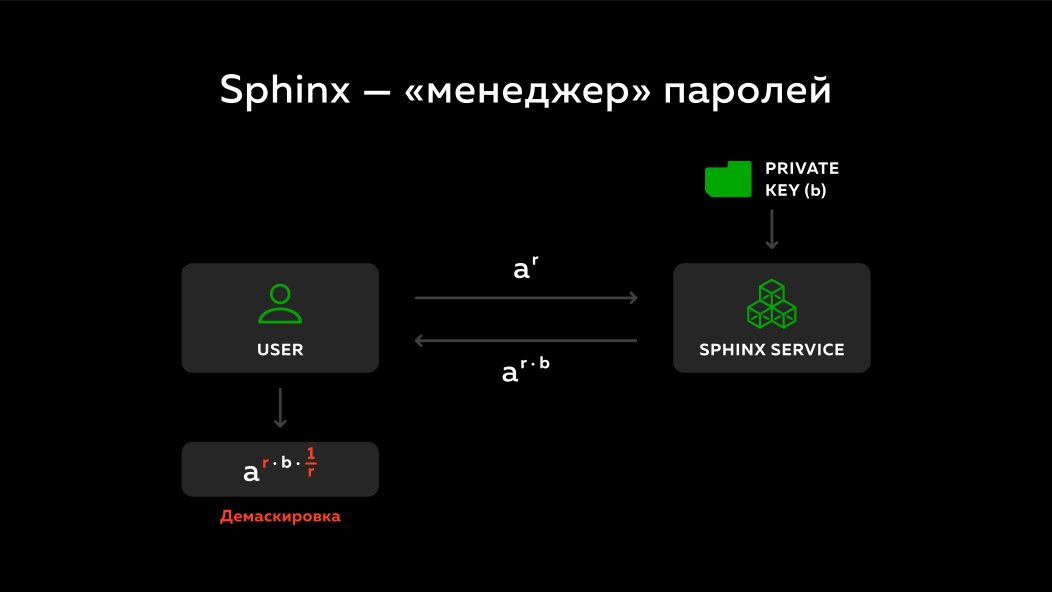
狮身人面像是做什么的? 再次有一个用户,有一个远程服务。 被屏蔽的号码将发送到该远程服务。 在远程服务上,有一个私钥b 。 他在做什么? 他将发送的数字a^r乘以他的密钥b并将其发回。 ( 《简编》的作者注意:在幻灯片上,发送的数字不是乘以私钥,而是提高到私钥的程度,但要点是 )。 由于数字r每次r不同,因此远程服务无法说出关于哪个密码和域被屏蔽的任何信息,即 每次他看到一些不同的随机数。 然后他简单地乘以他的私钥b并发回。
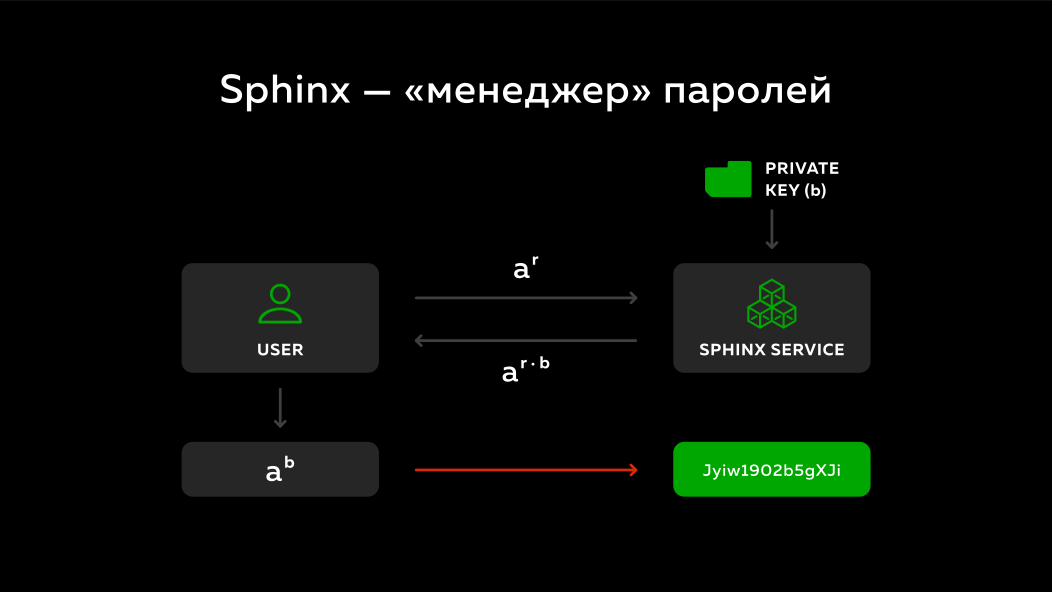
用户取消屏蔽服务器发送给他的内容,然后他得到一个数字-他的主密码,其域乘以服务器a^b私钥a^b 。 事实证明,他不知道服务器的密钥,服务器不知道用户向他发送了什么,但是最后他还获得了某种确定性数字。 每次执行此协议时,伪装都会有所不同,但结果始终是相同的,然后可以将此结果转回某种密码并用于进入各个站点。

真正出色的技术。 首先,您可以生成大型密码,即 它可以防止破裂。 其次,如果黑客获得了多个密码的访问权限,那么他将无法透露其他密码,因为 它们是彼此独立生成的。 第三,如果用户的密码消失在某个地方,那么这也将不会提供任何信息,因为黑客将不会获得密钥。 第四,它工作非常迅速,因为 这里不需要迭代的大哈希值,即 实际上执行了2-3次乘法,所有操作都立即生效。
但是该系统有其缺点。 用户正在与之交谈的服务器对他一无所知。 他只是简单地接收一些随机数作为输入,然后将它们乘以某值,然后将其发送回去。 客户端也对服务器一无所知,它向某处发送东西,接收结果,它可以正常工作。 但是,如果该服务发生任何事情,则用户将无法对此发表任何评论,他将没有任何信息。 密钥也不能更改;不能执行任何操作。
腐霉菌

会更好吗?

密码学家对这个系统进行了研究,并认为,是否有可能改进该系统并对其进行补充以使我们能够说它符合端到端原则? 即 客户端可以与服务器通信,但同时,它也可以对其进行身份验证并在一定程度上信任它。

他们提出了一种叫做Pythia的协议。

它是由伟人亚当·埃弗斯波 ( Adam Everspaugh)和他的同事们制作的。 是什么让它与众不同? 首先,服务知道谁输入密码,即 用户ID会通过密码传递到服务器。 它可以是旁边的一些随机ID框,也可以只是用户名。 没关系 但是服务知道这一点。 但是服务器不仅对此有所了解,而且可以严格地从数学上证明它是他。

如何运作? 有一个后端(某种Web服务,站点),还有一个Pythia服务。 后端做什么,服务做什么? 服务上有一个私钥k ,但它也将其公钥转移到后端。 服务的后端不仅发送Sphinx协议中的掩码数a^r ,而且还发送某种类型的用户标识符( UserID )。 该服务将用户ID和密码乘以其私钥,结果(UserID, a)^(r*k)发送后端。 他还发送回一定的Proof ,后端可以使用该Proof来检查服务器是否遭到黑客入侵,是否正在响应。

然后进行解屏蔽,结果将结果y放入DB。 在数据库中,我们不仅有一个哈希,而且还有一个椭圆曲线上的数字。

这里有一些有趣的观点:
- 服务器将用户标识和密码组合成一个数字的能力。 这称为双线性运算或双线性配对。 这是一个相对较新的数学,最近开始使用。 她拥有新数学家的所有特性,因为30年来还没有过去,因此每个人都可以确信这一切都是正常的。
- 但是发送服务的
Proof是相当古老的技术。 这称为Schnorr协议 。 公用密钥生成是基点乘以某个秘密密钥的乘积。 Schnorr协议证明,用于生成公共密钥的密钥用于将用户密码乘以相同的数字。 该协议已经存在很长时间了,在很多地方都使用过,它使您可以证明。 这就是所谓的零防证明 -服务器不显示其公钥,但是它表示我执行的操作是由我们最初同意的那个私钥执行的。

该系统的优点是什么?

而且她没有很多。
- 系统不加载后端。 由于后端执行所有操作,因此它将密码转换为数字,然后将其伪装,发送并随后对结果进行屏蔽。
- 如果从您那里窃取了具有此类数字的数据库,那么没有私钥对密码进行排序也就毫无意义。
- Pythia服务可以阻止蛮力尝试,这意味着后端原则上不必这样做。 如果他发现他们在相同的用户ID下尝试多次执行此转换操作,则可以简单地将其切断并以速率限制将其阻止。
- 由于伪装,该服务对密码一无所知。 每次将新的随机数发送给他。 只有用户标识符保持不变。
- 感谢ZKP(零知识证明),后端始终知道这是他曾经联系过的服务。
- 例如,如果您有一个包含哈希和盐的数据库,则可以为用户无缝迁移到这种解决方案。 他们甚至可能没有注意到任何东西。 取而代之的是用户密码,而不是用户密码,将其驱入Pythia,将来仅需使用此协议,获取数字
y ,然后再次将其放入数据库中即可。 然后可以删除哈希。 每次用户登录系统时,都会执行此协议,结果将获得一些数字,您可以将其与数据库中的数字进行比较。 身份验证系统本身将保持不变,因为 用户既可以更早登录,也可以使用相同的密码(甚至是弱密码)登录。 在这种情况下,系统将更加安全。

但是,这些还不是全部。

主要特征之一是,即使Pythia服务被黑客入侵,也可以生成新的私钥。 在我们的数据库中,存储的是数字,而不是哈希。 如果我们将旧密钥表示为数字k ,将新密钥表示为数字k' ,则可以计算一个称为更新令牌的数字。 为此,我们将新数字乘以与旧数字相反的数字。 使用此更新令牌,您可以遍历每个用户的数据库,并将此数字y乘以更新令牌。 完成此操作后,系统将继续使用远程服务上的新私钥工作。 这一切都是瞬间发生的。 如果发生灾难,则您的密码数据库被盗,您只需按一下手指就可以释放更新令牌,黑客从您那里窃取的事实立即变得毫无用处。 您只需在后台静静地浏览所有记录,然后更新它们,它们便会为您使用新的秘密密钥。 用户通常甚至都不会注意到任何东西。 即 密码数据库的无缝更新和即时失效是该系统的一些关键创新功能。

但这还不是全部。

位于基数中的数字大y ,它基本上大并且看起来很伪随机,即 不捡它很容易。 如果我们将后端具有的功能(例如,转移到客户端设备,电话)转移,则可以使用此y生成密钥。 我们称此为BrainKey。 这意味着用户在手机上的某个地方输入密码,还会伪装密码,然后将其发送到远程服务。 服务y返回某个数字y然后您可以使用此y生成一些非对称密钥。 因此,用户可以从他的密码中获得一个密钥对。 这被用于各种BrainWallets中 。 这是您输入密码并获取为其生成的比特币钱包的时间。 但是此应用程序不限于加密货币,它是一种数字签名,一些备份和帐户恢复功能,即 在使用非对称密码的地方,需要非对称密钥的地方。 所有这些都可以使用,但同时可以生成一对密钥,并且根据需要可以生成任意数量的密钥对。 因此,它们都将取决于用户的密码,这非常方便。

在一桶蜂蜜中,药膏并非没有苍蝇。

该技术的特点是它是非常新的。 它使用椭圆曲线,该曲线用于双线性运算( BLS12-381 )。 数学本身已经存在了一段时间,但是在我们的实现中特别使用的特定曲线仅在ZCash中使用,除了我们之外。 因此,可以使用一只手的手指来计数使用此新数学的库。 为了使它进入生产状态,您需要花费一些时间和精力。 然而,该行业并没有停滞不前,所有这些缺点都是暂时的。 由于前两个属性的影响,这些双线性运算的速度与现代数学(尤其是椭圆形)并不十分一致,当我们使用TLS协议,使用某些站点时,我们现在都使用它们。 一个核心上的服务大约有数百项操作。 实际上,这并没有阻止我们,在春季我们实施了该协议,将其发布到生产环境中并翻译了所有记录,并使用该协议保护了它们。 原则上,我们对当前任务的性能感到满意,如有必要,我们将使用Pythia服务提升另一个节点,并且原则上您已经可以使用所有这些。
苯丙氨酸

但是我们在考虑是否可以做得更好? 通过使用昨天的数学运算,可以实现毕生提供的属性吗? 不是明天,不是今天,而是昨天,已经使用了很多年。

实际上,在今年7月,科学家发布了一种称为“ 简单密码强化加密服务”(简称PHE)的新协议。

这是来自欧洲的科学家Russell Lai 。
这项服务的优势是什么? 首先,它使用标准的P-256曲线,该曲线在所有浏览器,产品中到处都有使用,默认曲线已经存在很多年了。 其次,这个东西的工作速度比Pythia快10倍,并且使用标准图元。 这有点困难,但是您可以自己动手实现它,而无需使用任何晦涩难懂的库。 您可以使用OpenSSL或Bouncy Castle等任何东西。

但这有点不同。 再次有一个后端,有一个PHE服务。 后端有一个公钥,服务有一个私钥y 。 与Pythia不同,注册过程和密码验证过程有所不同。 当新用户加入该服务并想要注册时,后端会做什么? 从一开始,他就要求PHE服务,请给我一些我可以用来注册的数据,某种注册记录。 服务说OK,然后用以下内容回答后端。 它会生成一些随机的32字节盐( sNonce )。 基于此盐及其私钥y,它生成两个数字,我们将其称为C0和C1 。 它还使用Schnorr协议(与以前的协议一样)生成证明(这是Proof这两个数字或2个点是使用其私钥y精确生成的)。 后端检查Proof 。 这里还没有密码。 后端做什么? 就他而言,他还拥有自己的个人客户端私钥x ,并且在从用户处收到密码后,他所做的工作与服务相同,只在其中添加了密码。 它需要一个随机的cNonce (随机客户盐),一个密码,并再次生成2个数字HC0和HC1 。 为什么是2? 因为第一个HC0用于身份验证,第二个数字HC1混合了一些随机数M乘以私钥x ( MC )。 M大小也是32个字节,以后可以用来加密用户数据(我们有Encryption Services)( 注释作者的注释:在这种情况下,加密密钥为MC )。 仅当用户输入正确的密码后, MC编号才可以用作密钥。 事实证明,在注册阶段,您不仅可以生成授权记录,还可以生成每个用户唯一的加密密钥,您可以使用该密钥加密其个人资料,一些数据以及其他内容。 然后,后端简单地将服务发送的内容与服务的内容加起来-将这些点加起来并得到T0和T1 。 在第一种情况下,它相加两个( C0 + HC0 ),在第二种情况下相加( C1 + HC1 + MC )。 然后,他输入了以2为底的盐( sNonce , cNonce ),借助它们获得了这些数字和2个数字( T0和T1 ),这些数字相加后得出。

因此,用户认证过程以相反的顺序发生。 用户在后端输入密码。 后端计算HC0并从数据库中计算出HC0 ,从T0减去HC0 ,并将结果C0与服务器盐一起发送到服务。 知道服务器盐的服务本身会计算出相同的点并进行查找,这与它是否发送了后端的事实相吻合,如果匹配,则密码是正确的,您可以用第二个数字C1回答,它将与该数字一起减去HC1 。 T1并获取加密密钥。 因此,PHE服务的密码甚至不会消失。 他甚至没有离开后端。 它采用某些点数乘以后端私钥的形式。 它甚至不存在,但是与此同时,远程服务可以就此密码是否正确做出严格的结论,并以此证明他使用私钥y进行了所有计算。

该系统有什么功能?

正如我所说,该密码不会离开后端。 但是与Pythia不同,您需要在后端使用私钥。 好吧,我们需要,需要保存在某个地方。 PHE具有腐霉菌的所有基本功能:
- 如果您使用私钥发生了某些事情,您也可以发出更新令牌。
- 您还可以浏览整个数据库,进行更新,一切都将保持原样。
- 搜索保护;
- 服务对密码一无所知;
- (Pythia , , , , PHE );
- .

...
… . . passw0rd.io . password , 18- , , zero trust, .. . , , .. Let's encrypt . , . CLI , . 2 SDK , GO .Net, .

:
- .
- .
- .

, .
?
37. ?

.
Q: , ! . , Pythia update token, ? private key . update token? 还是不行
A: , update token- .
Q: . - update token-, Private key ?
A: , update token-, , - , , , update token. , .. .
Q: , , , .
A: .. .
Q: , , , - Pythia - , , , ?
A: .
Q: ?
A: , Pythia . 即 , .
Q: ( ) bcrypt ?
A: , , , .
Q: , . ? , …
A: password
Q: password ? 火! 一般而言。
A: 123456 , 12345, 123456.
Q: . Pythia , PHE .
A: , .
Q: . . ? production ?
A: . 啊! Pythia.
Q: Pythia, , ?
A: .
Q: , ?
A: .
Q: , , !
A: SDK, .
Q: , , , , .. - , ? ? ?
A: , , , .. PHE, , 5 2 , 2 5 . , . PHE ( , ), , 10 , .
Q: .. - , - ? ?
A: . rate limiting, , .
Q: .. , ?
A: .
Q: . , .. Pythia (), , ? ?
A: , , .
Q: , update ?
A: , Pythia , , - - , , , )
A: ? ! . , , PHE, , .
结论
PHE ( ) + — ( , , ) ( ). PHE , .
:
, .
Scratch Virgil Security , , !
( )?
UPD : Scratch . . , . .