
因此,现在该讨论下一代多单元处理器:MultiClet S1。 如果这是您第一次听说它们,请确保在这些文章中查看建筑的历史和意识形态:
目前,正在开发新的处理器,但是已经出现了第一个结果,您可以评估它的功能。
让我们从最大的变化开始:基本功能。
特点
计划实现以下指标:
- 单元数:64
- 工艺流程:28 nm
- 时钟频率:1.6 GHz
- 芯片上的内存大小:8 Mb
- 晶体面积:40mm 2
- 消耗功率:6 W
实际数字将根据2019年制造样品的测试结果宣布。 除了芯片本身的特性外,该处理器还将支持高达16 GB的DDR4 3200MHz标准RAM,PCI Express总线和PLL。
应该注意的是,28 nm的制造工艺是最低的家用范围,不需要特殊的使用许可,因此是他的选择。 对于晶胞数量,考虑了不同的选择:128和256,但是随着晶体面积的增加,次品的百分比也会增加。 我们在64个细胞上定居,因此面积相对较小,这将使板上的合适晶体产量更高。 可以在
ICS(在此情况下为系统)的框架内进行进一步开发,
在这种情况下 ,可以在一个情况下组合多个64单元晶体。
必须说处理器的用途和用途正在发生根本变化。 S1不会像P1和R1那样是为嵌入而设计的微处理器,而是计算的加速器。 与GPGPU一样,可以将基于S1的板卡插入常规PC的PCI Express主板中,并用于数据处理。
建筑学
在S1中,“多单元格”现在是最小的计算单位:一组4个执行特定命令序列的单元格。 最初,计划将多单元电池组合在一起,称为联合执行命令的集群:一个集群必须包含4个多单元电池,晶体上总共有4个独立的集群。 但是,每个单元与群集中的所有其他单元具有完整的连接,并且随着键组的增加,它变得太多,这极大地使微电路的拓扑设计复杂化并降低其特性。 因此,他们决定放弃聚类划分,因为复杂性不能证明结果的合理性。 此外,为了获得最佳性能,在每个多单元上并行运行代码是最有益的。 总计,现在处理器包含16个独立的多单元。
一个多单元格虽然由4个单元格组成,但不同于4单元格R1,后者每个单元格都有自己的内存,自己的采样命令块,自己的ALU。 S1的排列略有不同。 ALU有2个部分:浮点运算块和整数运算块。 每个单元都有一个单独的整数块,但是在一个多单元中只有两个带浮点的块,因此有两对单元将它们分开。 这样做主要是为了减少晶体的面积:与整数算术相比,64位浮点算术占用了大量空间。 在每个单元上拥有这样的ALU被证明是多余的:获取命令不会提供ALU加载,并且它们是空闲的。 如实践所示,在减少ALU块的数量并保持获取命令和数据的步伐的同时,解决问题的总时间实际上没有改变或变化不大,并且ALU块已满载。 此外,浮点算术不像整数那样经常使用。
下图显示了处理器R1和S1的方框示意图。 在这里:
- CU(控制单元)-指令获取单元
- ALU FX-整数算术的算术逻辑单元
- ALU FP-浮点运算的算术逻辑单元
- DMS(数据存储器调度程序)-数据存储器控制单元
- DM-数据存储器
- PMS(程序存储器调度程序)-程序存储器控制单元
- PM-程序存储器
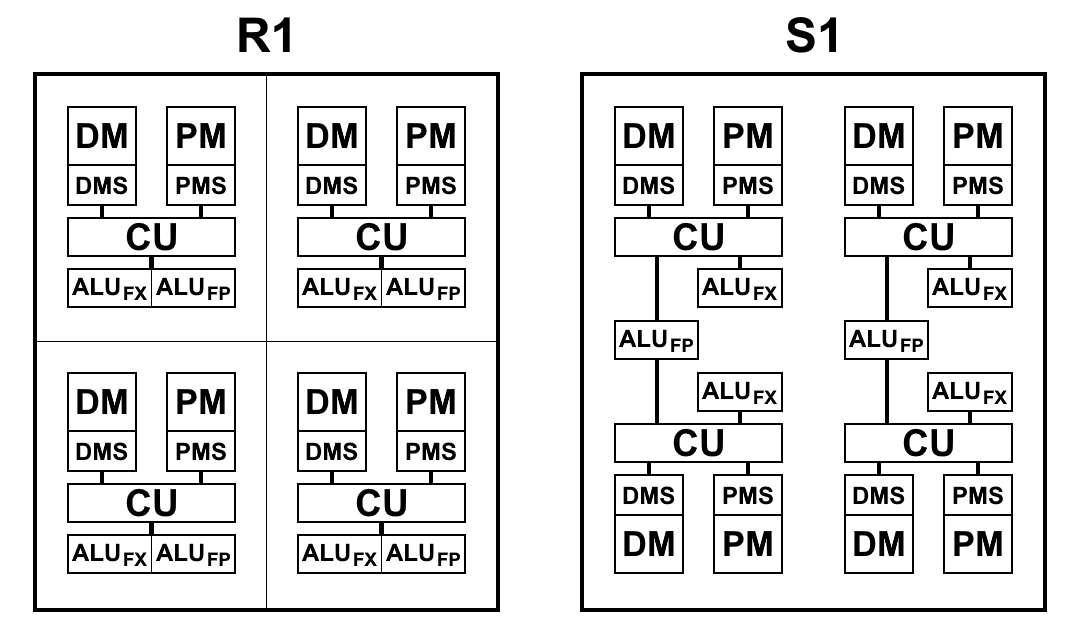
架构差异S1:
- 团队现在可以访问前面段落中的团队结果。 这是非常重要的更改,可让您在分支代码时显着加快转换速度。 处理器P1和R1别无选择,只能将所需的结果写入内存,并立即使用新段落中的第一个命令将它们读回。 即使在芯片上使用内存时,写入和读取操作也需要花费2到5个周期,只需参考上一段中的命令结果即可节省时间
- 现在,写入内存和寄存器的操作会立即进行,而不是在段落的末尾进行,这使您可以在段落的末尾开始编写命令。 结果,减少了段落之间的潜在停机时间。
- 该命令系统已经过优化,即:
- 添加了64位整数算法:加,减,32位数字的乘法,返回64位结果。
- 从内存读取的方法已更改:现在,对于任何命令,您都可以简单地指定要从中读取数据的地址作为参数,同时保留读取和写入命令的执行顺序。
这也使单独的内存读取命令过时了。 取而代之的是,在装入开关(以前称为get )中使用load value命令,将内存中的地址指定为参数:
.data foo: .long 0x1234 .text habr: load_l foo ; foo load_l [foo] ; 0x1234 add_l [foo], 0xABCD ; ; complete
- 添加了一种命令格式,允许使用2个常量参数。
以前,您只能将常量指定为第二个参数,第一个参数应始终是到开关中结果的链接。 该更改适用于所有两个参数的团队。 常量字段始终为32位,因此,例如,此格式允许使用一个命令生成64位常量。
那是:
load_l 0x12345678 patch_q @1, 0xDEADBEEF
它变成了:
patch_q 0x12345678, 0xDEADBEEF
- 修改和补充的矢量数据类型。
现在可以将以前称为“打包”数据类型的内容安全地称为矢量。 在P1和R1中,对压缩数字的运算仅采用一个常量作为第二个参数,即,例如,在相加时,矢量的每个元素都被添加了相同的数字,因此无法智能应用。 现在,可以将类似的运算应用于两个完整向量。 而且,这种使用向量的方式与LLVM中的向量机制完全一致,现在它允许编译器使用向量类型生成代码。
patch_q 0x00010002, 0x00030004 patch_q 0x00020003, 0x00040005 mul_ps @1, @2 ; - 00020006000C0014
- 处理器标志已删除。
结果,仅基于标志值的大约40个团队被删除。 这大大减少了团队数量,并因此减少了晶体面积。 现在,所有必要的信息都直接存储在交换单元中。
- 与零进行比较时,现在使用开关中的值代替零标志
- 现在代替符号标志,使用与命令类型相对应的位:字节为7,字节为15,短号为31,四线为63。 由于该字符最多乘以第63位,因此无论类型如何,您都可以比较不同类型的数字:
.data long: .long -0x1000 byte: .byte -0x10 .text habr: a := load_b [byte] ; 0xFFFFFFFFFFFFFFF0, ; byte 7 63. b := loadu_b [byte] ; 0x00000000000000F0, ; .. loadu_b c := load_l [long] ; 0xFFFFFFFFFFFFF000. ge_l @a, @c ; " " 1: ; 31 , . lt_s @a, @b ; 1, .. b complete
- 由于存在64位算术运算,因此不再需要进位标志
- 从段落到段落的过渡时间减少为1小节(而不是R1中的2-3)
基于LLVM的编译器
用于S1的C语言编译器类似于R1,并且由于体系结构没有根本改变,因此不幸的是,上一篇文章中描述的问题并未消失。
但是,在实施新命令系统的过程中,仅由于命令系统的更新,输出代码量本身就减少了。 此外,还有许多次要的优化将减少代码中的指令数量,其中一些已经完成(例如,使用一条指令生成64位常量)。 但是,还需要进行更认真的优化,并且可以按照效率和实现复杂性的升序来构建它们:
- 生成带有两个常量的所有两个参数的命令的能力。
通过patch_q生成64位常量只是一种特殊情况,但是我们需要一个通用的常量。 实际上,此优化的目的是允许团队仅将第一个参数替换为常量,因为第二个参数始终可以是常量,并且早就实现了。 这不是很常见的情况,但是,例如,当您需要调用一个函数并将其返回地址写入堆栈顶部时,可以
load_l func wr_l @1, #SP
优化以
wr_l func, #SP
- 通过任何命令中的参数替换内存访问的能力。
例如,如果您需要从内存中添加两个数字,则可以
load_l [foo] load_l [bar] add_l @1, @2
优化以
add_l [foo], [bar]
此优化是前一个优化的扩展,但是,这里已经需要进行分析:只有在此加法命令中仅使用加载的值一次且在其他任何地方都没有使用加载的值的情况下,才能进行这种替换。 如果仅在两个命令中使用读取结果,则从内存中读取一次作为单独的命令,而在另外两个命令中通过开关引用它,则更有利可图。
- 优化基本单元之间虚拟寄存器的传输。
对于R1,所有虚拟寄存器的传输都是通过内存进行的,这导致对内存的大量读取和写入,但是根本没有其他方法可以在段落之间传输数据。 S1允许您访问前几段命令的结果,因此,从理论上讲,可以删除许多内存操作,这将在所有优化中发挥最大的作用。 但是,这种方法仍然受到切换的限制:以前的结果不超过63个,因此可以像这样实现虚拟寄存器的每次传输。 如何做到这一点并不是一件容易的事,而且尚未解决解决这一问题的可能性。 编译器源可能会出现在公共领域,因此,如果任何人有想法并且您想加入开发,都可以这样做。
基准测试
由于处理器尚未在芯片上发布,因此很难评估其实际性能。 但是,RTL内核代码已经准备就绪,这意味着您可以使用仿真或FPGA进行评估。 为了运行以下基准测试,我们使用了ModelSim程序进行的仿真来计算确切的执行时间(以度量为单位)。 由于很难模拟整个晶体并且需要很长时间,因此模拟了一个多单元,结果乘以16(如果任务是为多线程设计的),因为每个多单元可以完全独立于其他单元工作。
同时,在Xilinx Virtex-6上执行了多单元建模,以测试真实硬件上处理器代码的性能。
芯标
CoreMark-一组测试,用于全面评估微控制器和中央处理器及其C编译器的性能。 如您所见,S1处理器既不是一个也不是另一个。 但是,它旨在执行绝对仲裁代码,即 任何可以在中央处理器上运行的人。 因此CoreMark适合评估S1的性能。
CoreMark包含链接列表,矩阵,状态机和
CRC和计算的功能。 通常,大多数代码严格按照顺序进行(测试多单元
硬件并行性的强度)并具有许多分支,这就是为什么编译器功能在最终性能中起着重要作用的原因。 编译后的代码包含许多简短的段落,尽管事实上它们之间的转换速度有所提高,但分支包括处理内存,我们希望最大程度地避免这种情况。
CoreMark计分卡:
| Multiclet R1(llvm编译器) | Multiclet S1(llvm编译器) | Elbrus-4C(R500 / E) | 德州仪器 AM5728 ARM Cortex-A15 | 贝加尔湖T1 | 英特尔酷睿i7 7700K |
|---|
| 制造年份 | 2015年 | 2019年 | 2014年 | 2018年 | 2016年 | 2017年 |
| 时钟频率,MHz | 100 | 1600 | 700 | 1500 | 1200 | 4500 |
| CoreMark总体得分 | 59 | 18356 | 1214 | 15789 | 13142 | 182128 |
| Coremark /兆赫 | 0.59 | 11.47 | 5.05 | 10.53 | 10.95 | 40.47 |
一个多单元的结果为1147,即0.72 / MHz,高于R1。 这谈到了在新处理器中开发多蜂窝体系结构的优势。
惠斯通
磨刀石-使用浮点数测量处理器性能的一组测试。 这里的情况要好得多:代码也是顺序的,但是没有大量分支,并且内部并发性好。
磨刀石由许多模块组成,您不仅可以测量整体结果,还可以测量每个特定模块的性能:
- 数组元素
- 数组作为参数
- 有条件的跳跃
- 整数运算
- 三角函数(tan,sin,cos)
- 程序调用
- 数组引用
- 标准函数(sqrt,exp,log)
它们分为几类:模块1、2和6衡量浮点运算的性能(MFLOPS1-3行); 模块5和8-数学函数(COS MOPS,EXP MOPS); 模块4和7-整数算术(FIXPT MOPS,EQUAL MOPS); 模块3-条件跳转(IF MOPS)。 在下表中,MWIPS的第二行是一般指标。
与CoreMark不同,Whetstone将在一个内核上进行比较,或者像本例一样在一个多单元上进行比较。 由于不同处理器的核心数量差异很大,因此,出于实验的纯度考虑,我们考虑每兆赫兹的指标。
磨刀石记分卡:
| 中央处理器 | MultiClet R1 | MultiClet S1 | 酷睿i7 4820K | ARM v8-A53 |
|---|
| 频率,MHz | 100 | 1600 | 3900 | 1300 |
| MWIPS / MHz | 0.311 | 0.343 | 0.887 | 0.642 |
| MFLOPS1 /兆赫 | 0.157 | 0.156 | 0.341 | 0.268 |
| MFLOPS2 /兆赫 | 0.153 | 0.111 | 0.308 | 0.241 |
| MFLOPS3 /兆赫 | 0.029 | 0.124 | 0.167 | 0.239 |
| COS MOPS /兆赫 | 0.018 | 0.008 | 0.023 | 0.028 |
| EXP MOPS /兆赫 | 0.008 | 0.005 | 0.014 | 0.004 |
| FIXPT MOPS / MHz | 0.714 | 0.116 | 0.998 | 1.197 |
| 中频MOPS / MHz | 0.081 | 0.196 | 1.504 | 1.436 |
| 等于MOPS / MHz | 0.143 | 0.149 | 0.251 | 0.439 |
Whetstone包含比CoreMark更直接的计算操作(在下面的代码中非常明显),因此请务必记住此处:浮点ALU的数量减半。 但是,与R1相比,计算速度几乎没有受到影响。
一些模块非常适合多单元架构。 例如,模块2在一个周期内计算许多值,并且由于处理器和编译器对双精度浮点数的完全支持,因此在编译后,我们得到了大而漂亮的段落,这些段落真正揭示了多单元体系结构的计算能力:
大型美观的120支队伍 pa: SR4 := loadu_q [#SP + 16] SR5 := loadu_q [#SP + 8] SR6 := loadu_l [#SP + 4] SR7 := loadu_l [#SP] setjf_l @0, @SR7 SR8 := add_l @SR6, 0x8 SR9 := add_l @SR6, 0x10 SR10 := add_l @SR6, 0x18 SR11 := loadu_q [@SR6] SR12 := loadu_q [@SR8] SR13 := loadu_q [@SR9] SR14 := loadu_q [@SR10] SR15 := add_d @SR11, @SR12 SR11 := add_d @SR15, @SR13 SR15 := sub_d @SR11, @SR14 SR11 := mul_d @SR15, @SR5 SR15 := add_d @SR12, @SR11 SR12 := sub_d @SR15, @SR13 SR15 := add_d @SR14, @SR12 SR12 := mul_d @SR15, @SR5 SR15 := sub_d @SR11, @SR12 SR16 := sub_d @SR12, @SR11 SR17 := add_d @SR11, @SR12 SR11 := add_d @SR13, @SR15 SR13 := add_d @SR14, @SR11 SR11 := mul_d @SR13, @SR5 SR13 := add_d @SR16, @SR11 SR15 := add_d @SR17, @SR11 SR16 := add_d @SR14, @SR13 SR13 := div_d @SR16, @SR4 SR14 := sub_d @SR15, @SR13 SR15 := mul_d @SR14, @SR5 SR14 := add_d @SR12, @SR15 SR12 := sub_d @SR14, @SR11 SR14 := add_d @SR13, @SR12 SR12 := mul_d @SR14, @SR5 SR14 := sub_d @SR15, @SR12 SR16 := sub_d @SR12, @SR15 SR17 := add_d @SR15, @SR12 SR15 := add_d @SR11, @SR14 SR11 := add_d @SR13, @SR15 SR14 := mul_d @SR11, @SR5 SR11 := add_d @SR16, @SR14 SR15 := add_d @SR17, @SR14 SR16 := add_d @SR13, @SR11 SR11 := div_d @SR16, @SR4 SR13 := sub_d @SR15, @SR11 SR15 := mul_d @SR13, @SR5 SR13 := add_d @SR12, @SR15 SR12 := sub_d @SR13, @SR14 SR13 := add_d @SR11, @SR12 SR12 := mul_d @SR13, @SR5 SR13 := sub_d @SR15, @SR12 SR16 := sub_d @SR12, @SR15 SR17 := add_d @SR15, @SR12 SR15 := add_d @SR14, @SR13 SR13 := add_d @SR11, @SR15 SR14 := mul_d @SR13, @SR5 SR13 := add_d @SR16, @SR14 SR15 := add_d @SR17, @SR14 SR16 := add_d @SR11, @SR13 SR11 := div_d @SR16, @SR4 SR13 := sub_d @SR15, @SR11 SR4 := loadu_q @SR4 SR5 := loadu_q @SR5 SR6 := loadu_q @SR6 SR7 := loadu_q @SR7 SR15 := mul_d @SR13, @SR5 SR8 := loadu_q @SR8 SR9 := loadu_q @SR9 SR10 := loadu_q @SR10 SR13 := add_d @SR12, @SR15 SR12 := sub_d @SR13, @SR14 SR13 := add_d @SR11, @SR12 SR12 := mul_d @SR13, @SR5 SR13 := sub_d @SR15, @SR12 SR16 := sub_d @SR12, @SR15 SR17 := add_d @SR15, @SR12 SR15 := add_d @SR14, @SR13 SR13 := add_d @SR11, @SR15 SR14 := mul_d @SR13, @SR5 SR13 := add_d @SR16, @SR14 SR15 := add_d @SR17, @SR14 SR16 := add_d @SR11, @SR13 SR11 := div_d @SR16, @SR4 SR13 := sub_d @SR15, @SR11 SR15 := mul_d @SR13, @SR5 SR13 := add_d @SR12, @SR15 SR12 := sub_d @SR13, @SR14 SR13 := add_d @SR11, @SR12 SR12 := mul_d @SR13, @SR5 SR13 := sub_d @SR15, @SR12 SR16 := sub_d @SR12, @SR15 SR17 := add_d @SR15, @SR12 SR15 := add_d @SR14, @SR13 SR13 := add_d @SR11, @SR15 SR14 := mul_d @SR13, @SR5 SR13 := add_d @SR16, @SR14 SR15 := add_d @SR17, @SR14 SR16 := add_d @SR11, @SR13 SR11 := div_d @SR16, @SR4 SR13 := sub_d @SR15, @SR11 SR15 := mul_d @SR13, @SR5 SR13 := add_d @SR12, @SR15 SR12 := sub_d @SR13, @SR14 SR13 := add_d @SR11, @SR12 SR12 := mul_d @SR13, @SR5 SR13 := sub_d @SR15, @SR12 SR16 := sub_d @SR12, @SR15 SR17 := add_d @SR14, @SR13 SR13 := add_d @SR11, @SR17 SR14 := mul_d @SR13, @SR5 SR5 := add_d @SR16, @SR14 SR13 := add_d @SR11, @SR5 SR5 := div_d @SR13, @SR4 wr_q @SR15, @SR6 wr_q @SR12, @SR8 wr_q @SR14, @SR9 wr_q @SR5, @SR10 complete
弹出
为了反映架构本身的特性(与编译器无关),我们将考虑架构的所有功能来衡量用汇编程序编写的内容。 例如,以512位数字(popcnt)计数单位位。 为了清楚起见,我们将采用一个多像元的结果,以便可以将它们与R1进行比较。
比较表,每32位计算周期的时钟周期数:
| 演算法 | Multiclet r1 | Multiclet S1(一个多单元) |
|---|
| 比特黑客 | 5.0 | 2.625 |
这里使用了新的更新的矢量指令,与R1汇编器中实现的相同算法相比,它使我们的指令数量减少了一半。 工作速度分别提高了近2倍。
弹出 bithacks: b0 := patch_q 0x1, 0x1 v0 := loadu_q [v] v1 := loadu_q [v+8] v2 := loadu_q [v+16] v3 := loadu_q [v+24] v4 := loadu_q [v+32] v5 := loadu_q [v+40] v6 := loadu_q [v+48] v7 := loadu_q [v+56] b1 := patch_q 0x55555555, 0x55555555 i00 := slr_pl @v0, @b0 i01 := slr_pl @v1, @b0 i02 := slr_pl @v2, @b0 i03 := slr_pl @v3, @b0 i04 := slr_pl @v4, @b0 i05 := slr_pl @v5, @b0 i06 := slr_pl @v6, @b0 i07 := slr_pl @v7, @b0 b2 := patch_q 0x33333333, 0x33333333 i10 := and_q @i00, @b1 i11 := and_q @i01, @b1 i12 := and_q @i02, @b1 i13 := and_q @i03, @b1 i14 := and_q @i04, @b1 i15 := and_q @i05, @b1 i16 := and_q @i06, @b1 i17 := and_q @i07, @b1 b3 := patch_q 0x2, 0x2 i20 := sub_pl @v0, @i10 i21 := sub_pl @v1, @i11 i22 := sub_pl @v2, @i12 i23 := sub_pl @v3, @i13 i24 := sub_pl @v4, @i14 i25 := sub_pl @v5, @i15 i26 := sub_pl @v6, @i16 i27 := sub_pl @v7, @i17 i30 := and_q @i20, @b2 i31 := and_q @i21, @b2 i32 := and_q @i22, @b2 i33 := and_q @i23, @b2 i34 := and_q @i24, @b2 i35 := and_q @i25, @b2 i36 := and_q @i26, @b2 i37 := and_q @i27, @b2 i40 := slr_pl @i20, @b3 i41 := slr_pl @i21, @b3 i42 := slr_pl @i22, @b3 i43 := slr_pl @i23, @b3 i44 := slr_pl @i24, @b3 i45 := slr_pl @i25, @b3 i46 := slr_pl @i26, @b3 i47 := slr_pl @i27, @b3 b4 := patch_q 0x4, 0x4 i50 := and_q @i40, @b2 i51 := and_q @i41, @b2 i52 := and_q @i42, @b2 i53 := and_q @i43, @b2 i54 := and_q @i44, @b2 i55 := and_q @i45, @b2 i56 := and_q @i46, @b2 i57 := and_q @i47, @b2 i60 := add_pl @i50, @i30 i61 := add_pl @i51, @i31 i62 := add_pl @i52, @i32 i63 := add_pl @i53, @i33 i64 := add_pl @i54, @i34 i65 := add_pl @i55, @i35 i66 := add_pl @i56, @i36 i67 := add_pl @i57, @i37 b5 := patch_q 0xf0f0f0f, 0xf0f0f0f i70 := slr_pl @i60, @b4 i71 := slr_pl @i61, @b4 i72 := slr_pl @i62, @b4 i73 := slr_pl @i63, @b4 i74 := slr_pl @i64, @b4 i75 := slr_pl @i65, @b4 i76 := slr_pl @i66, @b4 i77 := slr_pl @i67, @b4 b6 := patch_q 0x1010101, 0x1010101 i80 := add_pl @i70, @i60 i81 := add_pl @i71, @i61 i82 := add_pl @i72, @i62 i83 := add_pl @i73, @i63 i84 := add_pl @i74, @i64 i85 := add_pl @i75, @i65 i86 := add_pl @i76, @i66 i87 := add_pl @i77, @i67 b7 := patch_q 0x18, 0x18 i90 := and_q @i80, @b5 i91 := and_q @i81, @b5 i92 := and_q @i82, @b5 i93 := and_q @i83, @b5 i94 := and_q @i84, @b5 i95 := and_q @i85, @b5 i96 := and_q @i86, @b5 i97 := and_q @i87, @b5 iA0 := mul_pl @i90, @b6 iA1 := mul_pl @i91, @b6 iA2 := mul_pl @i92, @b6 iA3 := mul_pl @i93, @b6 iA4 := mul_pl @i94, @b6 iA5 := mul_pl @i95, @b6 iA6 := mul_pl @i96, @b6 iA7 := mul_pl @i97, @b6 iB0 := slr_pl @iA0, @b7 iB1 := slr_pl @iA1, @b7 iB2 := slr_pl @iA2, @b7 iB3 := slr_pl @iA3, @b7 iB4 := slr_pl @iA4, @b7 iB5 := slr_pl @iA5, @b7 iB6 := slr_pl @iA6, @b7 iB7 := slr_pl @iA7, @b7 wr_q @iB0, c wr_q @iB1, c+8 wr_q @iB2, c+16 wr_q @iB3, c+24 wr_q @iB4, c+32 wr_q @iB5, c+40 wr_q @iB6, c+48 wr_q @iB7, c+56 complete
以太坊
基准当然很好,但是我们有一个特定的任务:制造一个计算加速器,很高兴知道它如何处理现实世界中的任务。 现代加密货币最适合这种验证,因为挖掘算法在许多不同的设备上运行,因此可以作为比较的基准。 我们从直接在采矿设备上运行的以太坊和Ethash算法开始。
以太坊的选择基于以下考虑。 如您所知,诸如比特币之类的算法可以通过专用ASIC芯片非常有效地实现,因此由于性能低和功耗高,使用处理器或视频卡开采比特币及其克隆在经济上变得不利。 为了摆脱这种情况,矿工社区正在开发基于其他算法原理的加密货币,重点是开发使用通用处理器或视频卡进行挖掘的算法。 这种趋势将来可能会继续。 以太坊是基于这种方法的最著名的加密货币。 挖矿以太坊的主要工具是视频卡,就效率(哈希率/ TDP)而言,视频卡明显(数倍)领先于通用处理器。
Ethash是一种所谓的
内存绑定算法,即 它的计算时间主要受内存数量和速度的限制,而不受计算本身速度的限制。 现在,对于以太坊挖矿来说,视频卡是最合适的,但是它们同时执行许多操作的能力并没有太大帮助,并且它们仍然取决于RAM的速度,这在
本文中已得到明显证明。 从那里,您可以拍摄一张图片,说明算法的操作,以解释为什么会发生这种情况。
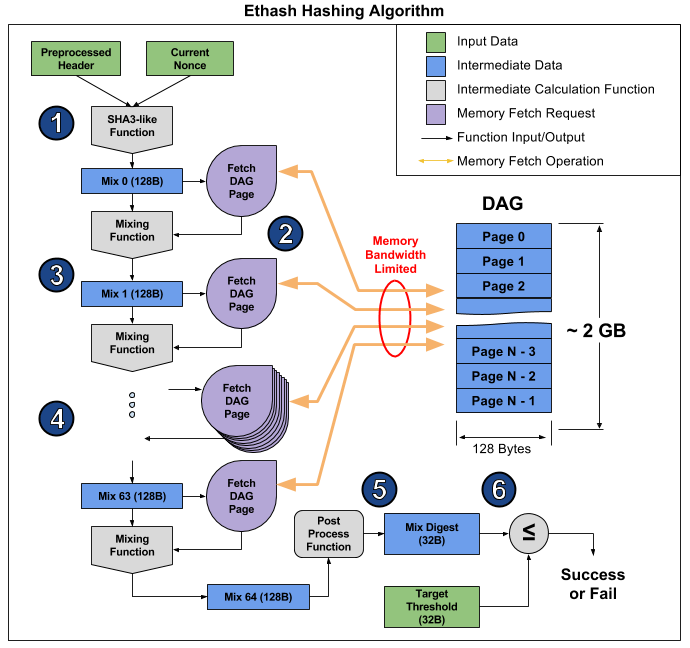
本文将算法分为6点,但可以将其分为3个阶段以更加明显:
- 开始:SHA-3(512)计算原始的128字节混合0(点1)
- 通过读取接下来的128个字节并通过混合功能将它们与先前的字节混合,来对Mix数组进行64倍的重新计算,总计8 KB(第2-4段)
- 完成并验证结果
从RAM中读取随机的128个字节所花费的时间比看起来要多得多。 如果您使用的MSI RX 470图形卡具有2048个计算设备,最大内存带宽为211.2 GB / s,则要配备每个设备,您需要1 /(211.2 GB /(128 b * 2048))= 1241 ns,或大约1496 ns以给定的频率循环。 给定混合函数的大小,我们可以假设从视频卡读取内存要比重新计算接收到的信息花费更长的时间。 结果,算法的第2阶段要花费很多时间,比第1和第3阶段要长得多,尽管它们包含更多的计算(主要在SHA-3中),但最终对性能的影响很小。 您可以看一下此显卡的哈希率:理论上为26.375兆每秒/秒(仅受内存带宽限制),而实际为24兆每秒/秒,也就是说,阶段1和3仅花费10%的时间。
在S1上,所有16个多单元都可以并行工作,并且可以使用不同的代码。 此外,还将在一个通道上安装8个多单元的双通道RAM。 在Ethash算法的第2阶段,我们的计划如下:一个多单元从内存中读取128个字节并开始对其重新计数,然后下一个多单元读取内存并重新计数,依此类推,直到第8个,即 在读取128字节的内存后,一个多单元具有7 * [128字节的读取时间]来重新计算数组。 假设这样的读取将花费16个周期,即。 给出了112种重新计算的措施。 计算混合函数大约需要相同的时钟周期,因此S1接近内存带宽与处理器性能的理想比率。 由于在第二阶段中不会浪费时间,因此应尽可能优化算法的其余部分,因为这会真正影响性能。
为了评估计算速度SHA-3(Keccak),开发并测试了C程序,目前正在此程序的基础上创建其最佳版本。评估编程显示,一个多单元电池可在1550个时钟周期内执行SHA-3(Keccak)计算。因此,一个多像元进行一次哈希运算的总时间为1550 + 64 *(16 + 112)= 9742个周期。在1.6 GHz频率和16个并行多单元的情况下,处理器的哈希率将为2.6 MHash / s。| 促进剂 | MultiClet S1 | NVIDIA GeForce GTX 980 Ti | Radeon RX 470 | Radeon RX Vega 64 | NVIDIA GeForce GTX 1060 | NVIDIA GeForce GTX 1080 Ti |
|---|
| 价钱 | | $ 650 | $ 180 | $ 500 | $ 300 | $ 700 |
| 哈希率 | 2.6 MHash /秒 | 21.6 MHash /秒 | 25.8 MHash /秒 | 43.5 MHash /秒 | 25 MHash / s | 55 MHash / s |
| 技术开发计划 | 6瓦 | 250瓦 | 120瓦 | 295瓦 | 120瓦 | 250瓦 |
| 哈希率/ TDP | 0.43 | 0.09 | 0.22 | 0.15 | 0.22 | 0.21 |
| 工艺技术 | 28纳米 | 28纳米 | 14纳米 | 14纳米 | 16纳米 | 16纳米 |
当使用MultiClet S1作为挖掘工具时,板上实际上可以安装20个或更多处理器。在这种情况下,这样的电路板的哈希率将等于或高于现有视频卡的哈希率,而具有S1的电路板的功耗将仅为拓扑标准为16和14 nm的视频卡的一半。总之,我必须说,现在的主要任务是为多单元加密货币矿机和超级计算矿机制造多处理器板。由于功耗和架构小,计划实现竞争力,非常适合于任意计算。该处理器仍在开发中,但是您已经可以在汇编器中开始编程,以及评估编译器的当前版本。已经有一个最小的SDK,其中包含汇编程序,链接器,编译器和功能模型,您可以在其上启动和测试程序。