嘿,堆满了,让我们训练技能。 在我看来,我建议揉捏陀螺,使用另一种不同寻常的范式进行此操作很有趣。 大多数开发人员都具有算法开发的技巧-任务变成需要连接的模块,以思考导致所需结论的移动顺序。
在这里,一周前提到了序言,我想回答一下,序言语言适合解决问题。 我已经谈到了这个主题,并列举了一个带有算法任务的站点可以为我提供的几种随机任务解决方案,我想展示一下,任何复杂的解决方案都可以使用声明性语言,并且运行速度不会变慢(嗯,也许很明显)不太慢)。
花了很长时间才提出下一个问题,并且已经收到第一个解决方案,我演示了问题并找出了它的速度。
序言很有趣,因为您可以创建一个演绎程序,该程序可以显示很多解决方案,甚至可以限制它,但没有提供迭代的方法,
该算法将被开发 解算器 口译员。
因此,任务是这样的 :
- 困雨ii
给定一个正整数的mxn矩阵,该矩阵表示2D高程图中每个晶胞的高度,计算出下雨后它能捕获的水量。
注意事项:
m和n均小于110。每个晶胞的高度大于0且小于20,000。
范例:
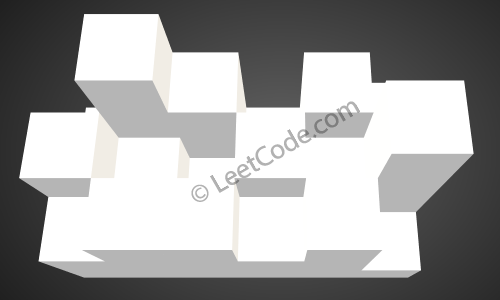
给出以下3x6高度图:
[
[1,4,3,1,3,2],
[3,2,1,3,2,4],
[2,3,3,2,3,1]
]
返回4。
经过漫长的尝试来提出解决方案之后,我想到了这样的措辞:
有必要将最大量的水倒入每个电池中,这样不会溢出水 。 我建议在每个单元格中倒入一定量的水,但要使其小于所有可能的最大值。
原来是这样的:
reptest(X0,X2):- flatten(X0,FX0), sort(0,>,FX0,Vals), repdown(X0,Vals,X0,X2),!.
该谓词接受输入列表(矩阵),并将其转换为解决方案,转换为矩阵,其中还有其他值将是有效答案。 然后另一个谓词逐个元素地获取这两个列表,并求出总数。
repdown(X0,Vals,X,X1):- puts(Vals,X0,X1), X\=X1, balns(X0,X1),!. repdown(_,_,X,X).
该谓词将采用一种解决方案,并检查它是否“正常”填充,如果满足问题的条件,则这是解决方案。
这是“生成并验证”方法,我们说该值在这样的集合中,然后修改该集合的所有元素,并检查某种退出条件。
因此,接下来我将获得带有puts(Vals,X0,X1)谓词的新解决方案,这里首先是此矩阵中所有可能的高度的列表,我们将从中为每个单元格选择可能的高度。 根据输入测试的分析,发现在此问题中,如果在其周围可以插入太多水而将其倒在“头上”,则有可能填充整个单元。
总体而言,该谓词看起来更复杂,有必要处理组成一个3x3正方形的三行线(是的,Prolog中没有数组,但是它看起来像输入数据的描述,我们在声明性编程中使用它,您可能不知道数组中元素的索引,只有一个列表的头部和尾部,因此只需描述一个与输入规范匹配的模板即可。
puts(_,[],[]). puts(_,[X],[X]). puts(_,[X,Z],[X,Z]). puts(V,[R1,R2,R3|T],[R1|St]) :- number(R2),!,sel_biger(R2,V,R21),puts(V,[R21,R3|T],St). puts(V,[R1,R2,R3|T],[R1|St]) :- puts(V,R2,R21),puts(V,[R21,R3|T],St).
事实就是这样来表达绕过矩阵的方式,您可以从中获取前三行(以及更多行),从中也可以从左至右选择元素的三元组,并且在八个邻居之间将有一个景观的[Itaya] [Utaya]像元。 借助于sel_biger(R2,V,R21),该单元格有了新的含义。
可以将该值设置为当前单元格,它可以是可能的高度之一,甚至列表按降序排列,因此第一个将是所有可用的最高高度,然后是其后的最高高度:
sel_biger(C,[H|_],H):-H>=C. sel_biger(C,[_|T],X):-sel_biger(C,T,X).
这是对“决策生成器”的描述,然后您需要确保从每个点上任意填充的高度获得的矩阵与我们所需的答案相似。
并且需要找到一种状态,使水沉淀在孔中,我将尝试这样写:
一个正方形的9个值中的3个乘以3,在中心应始终有一个高度,使其与输入映射图不矛盾,这样就不会获得这些单元格中原来的平衡变化,如果有高度,则即使在其上方也不应有单元格,即使一切都会被水淹没,那么在这里我们可以说,高级单元格应该独自保留或用更高的值替换,但是要使其等于所有邻居,即 电流左侧,右侧和从上至下的单元格应该超过或相等,如果单元格中有更多的水,则只有当水位上升时...
最后两个谓词(采用输入矩阵)开始搜索合适的结果,将元素之间的总和相减,然后找到问题中所需的最终总和:
diffall(L0,L2,S):- flatten(L0,F0),sum_list(F0,S0), flatten(L2,F2),sum_list(F2,S2), S is S2-S0. %% , sums(X,S):-reptest(X,X1),diffall(X,X1,S).
我将演示该站点提供的测试。
reptest(X0,X2):- flatten(X0,FX0), sort(0,>,FX0,Vals), repdown(X0,Vals,X0,X2),!. repdown(X0,Vals,X,X1):- puts(Vals,X0,X1), X\=X1, balns(X0,X1),!. repdown(_,_,X,X). puts(_,[],[]). puts(_,[X],[X]). puts(_,[X,Z],[X,Z]). puts(V,[R1,R2,R3|T],[R1|St]) :- number(R2),!,sel_biger(R2,V,R21),puts(V,[R21,R3|T],St). puts(V,[R1,R2,R3|T],[R1|St]) :- puts(V,R2,R21),puts(V,[R21,R3|T],St). sel_biger(C,[H|_],H):-H>=C. sel_biger(C,[_|T],X):-sel_biger(C,T,X). % balns([],[]). balns([_],[_]). balns([_,_],[_,_]). balns([B1,B2,B3|Tb],[R1,R2,R3|T]) :- blevel(B1,B2,B3,R1,R2,R3), balns([B2,B3|Tb],[R2,R3|T]). % , 33 blevel([],[],[],[],[],[]). blevel([_],[_],[_],[_],[_],[_]). blevel([_,_],[_,_],[_,_],[_,_],[_,_],[_,_]). blevel([_,U1,U2|Tu],[R,C,L|T],[_,B1,B2|Tb], [_,U10,U20|Tu0],[R0,C0,L0|T0],[_,B10,B20|Tb0]):- equ(C,[U1,L,R,B1],C0,[U10,L0,R0,B10]), blevel([U1,U2|Tu],[C,L|T],[B1,B2|Tb], [U10,U20|Tu0],[C0,L0|T0],[B10,B20|Tb0]). % , % equ(_,[],_,[]):-!. equ(C,_,C,_):-!. equ(C0,_,C,N):-C>C0,!,findall(X,(member(X,N),X<C),[]). equ(C0,[C0|T0],C,[C|T]):-!,equ(C0,T0,C,T). diffall(L0,L2,S):- flatten(L0,F0),sum_list(F0,S0), flatten(L2,F2),sum_list(F2,S2), S is S2-S0. sums(X,S):-reptest(X,X1),diffall(X,X1,S). %unit-tests framework assert_are_equal(Goal, false):-get_time(St),not(Goal),!,get_time(Fin),Per is round(Fin-St),writeln(Goal->ok:Per/sec). assert_are_equal(Goal, true):- get_time(St),Goal, !,get_time(Fin),Per is round(Fin-St),writeln(Goal->ok:Per/sec). assert_are_equal(Goal, Exp):-writeln(Goal->failed:expected-Exp). :-assert_are_equal(sums([[1,4,3,1,3,2],[3,2,1,3,2,4],[2,3,3,2,3,1]],4),true). :-assert_are_equal(sums([[1,3,3,1,3,2],[3,2,1,3,2,3],[3,3,3,2,3,1]],4),true). :-assert_are_equal(sums([[12,13,1,12],[13,4,13,12],[13,8,10,12],[12,13,12,12],[13,13,13,13]],14),true). :-assert_are_equal(sums([[2,3,4],[5,6,7],[8,9,10],[11,12,13],[14,15,16]],0),true). :-assert_are_equal(sums([],0),true). :-assert_are_equal(sums([[1]],0),true). :-assert_are_equal(sums([[2,3]],0),true). :-assert_are_equal(sums([[3],[2]],0),true). :-assert_are_equal(sums([[18,2,3],[4,5,6],[7,8,9]],0),true). :-assert_are_equal(sums([[3,5,5],[5,4,5],[5,5,5]],1),true). :-assert_are_equal(sums([[5,5,5,1],[5,1,1,5],[5,1,5,5],[5,2,5,8]],3),true). :-assert_are_equal(sums([[2,2,2],[2,1,2],[2,1,2],[2,1,2]],0),true). :-assert_are_equal(sums([[17,2,3,4,5,6,7,8,9,10]],0),true). :-assert_are_equal(sums([[9,9,9,9,9],[9,2,1,2,9],[9,2,8,2,9],[9,2,3,2,9],[9,9,9,9,9]],57),true). %:-assert_are_equal(sums([[9,9,9,9,9,9,8,9,9,9,9],[9,0,0,0,0,0,1,0,0,0,9],[9,0,0,0,0,0,0,0,0,0,9],[9,0,0,0,0,0,0,0,0,0,9],[9,9,9,9,9,9,9,9,9,9,9]],215),true). :-assert_are_equal(sums([[11,21,31],[81,9,41],[17,61,51]],12),true). :-assert_are_equal(sums([[3,3,4,4,4,2],[3,1,3,2,1,4],[7,3,1,6,4,1]],5),true). %:-assert_are_equal(sums([[78,16,94,36],[87,93,50,22],[63,28,91,60],[64,27,41,27],[73,37,12,69],[68,30,83,31],[63,24,68,36]],44),true).
我不得不对测试发表评论 。 并非所有经历。
任务是如何加快速度?
某些解决方案由于长期寻找解决方案而无法找到,它们的生成顺序太慢,这里的复杂度可能为n !,对数组每个单元的所有可能值进行了排序。
在限制条件下在编程系统中表达此任务很方便,就像在Prolog中这样称呼它: CLP(FD):有限域上的约束逻辑编程。
clp(fd)是标准SWI-Prolog发行版中包含的库。 它解决了涉及变量集的问题,其中需要满足变量之间的关系。
>>
我提出这样的问题:
我们需要这样一个列表,在整个地图中,值集中的每个元素都大于或等于其最大值,同时考虑到必须按相应的溢出液体顺序清楚地放置这些元素的限制 。
这就是我从输入列表开始的操作,输入列表是一个新列表,其元素在给定范围内(从当前元素的R2值到V的最大值)变得未知
在输入处是列表列表;在输出处是具有最大值分布的新列表,
满足“流体平衡”标尺的限制:
checks(X0,X2):- flatten(X0,FX), max_list(FX,Max),checks(Max,X0,X2), balns(X0,X2), flatten(X2,FX2), labeling([down],FX2). checks(_,[],[]). checks(_,[X],[X]). checks(_,[X,Z],[X,Z]). checks(V,[R1,R2,R3|T],[R1|St]) :- number(R2),!, R21 in R2..V, checks(V,[R21,R3|T],St). checks(V,[R1,R2,R3|T],[R1|St]) :- checks(V,R2,R21),checks(V,[R21,R3|T],St).
这既是生成器,又是支票,这表明元素在这样的集合中,然后逐渐施加支票,这套收窄了。 此外,还保留一些东西,并且可以对其进行“标记”,即 设置将满足所有约束之和的整数值。 呼叫标签([向下],FX2)强制填充(接触) 变数 带有特定值的未知数,并且可能有几个这样的选项,但是我们将始终采用第一个选项,因为据说所有变量在搜索中从上界向下移动,这些都是[down]搜索选项。
在这里,您可以看到以下复杂设置:16.2.1。 变量选择策略
变量选择策略使您可以指定接下来标记哪个Vars变量,并且是以下变量之一:
最左侧-按照变量在变量中出现的顺序标记变量。 这是默认值。
ff第一次失败。 接下来用最小的域标记最左边的变量,以便及早发现不可行。 当选择第一个变量时,后续变量的域很小时,这通常是一个好策略。
ffc在具有最小域的变量中,接下来标记参与最多约束的最左边的变量。 应用约束必须删除子树,因此这可能是一个不错的策略。
min标记最左边的变量,其下限是下一个最低的变量。 请注意,这是min / 0,不同于min / 1,它确定解决方案,并在上一节中进行了讨论。 如果您试图最小化某些可能因各种变量而降低的全局值(例如最小成本解决方案),则这是一个很好的策略。
max标记最左边的变量,其上限为下一个最高的变量。 这也与max / 1不同。 当尝试最大化全局值时,有关min的建议也适用于max。
16.2.2。 价值订单
值顺序是以下之一:
向上按升序尝试所选变量域的元素。 这是默认值。
向下尝试按降序排列域元素。
显然,如果您的分布不对称(如我们在上面如何有效标记的示例所示),请尝试最常见的一阶元素。
16.2.3。 分支策略
分支策略是以下之一:
步骤对于每个变量X,在X = V和X#\ = V之间进行选择,其中V由值排序选项确定。 这是默认值。
枚举对于每个变量X,对于X域的所有值V_i,在X = V_1,X = V_2等之间进行选择。该顺序由值排序选项确定。
二等分对于每个变量X,在X#= <M和X#> M之间进行选择,其中M是X的域的中点。如果许多变量是整数范围内的选择,则选择此选项。而不是一组枚举值中的一个(例如百分比,vs a = 0,b = 1,c = 2)
现在实际上是“平衡的”是当浇注的水没有从一个单元到另一个单元溢出时。 这是元素的初始顺序的对应关系。 您可能会认为填充单元格将保留原始景观的形状,这意味着如果有墙,则可以在其上覆盖水,这样它就必须等于其所有邻居,或者如果它不是被水覆盖的墙...
考虑平衡的情况:
-如果单元被淹没,则在同一甚至更高的位置旁边(突然是墙)。
-如果该单元格等于相邻的那个单元格,那么它应该等于新的相邻的那个单元格。
-在极端情况下,该牢房并没有改变其含义,而她仍然是什么样的邻居:
这样可以将对任务的态度转移到程序中。 对我而言,没有必要考虑决策算法,而是提供对结果的正确描述,正确设置所有初始约束(值集)非常重要。 这种方法可以简单地与常规搜索“混合”在一起,并具有Prolog固有的返回和递归功能。 与使用经典的 Prolog方法相比,这种方法可以制定更多的声明式程序。
我将通过一组测试给出获得的解决方案:
:- use_module(library(clpfd)). checks(X0,X2):- flatten(X0,FX), max_list(FX,Max),checks(Max,X0,X2), balns(X0,X2), flatten(X2,FX2), labeling([down],FX2). checks(_,[],[]). checks(_,[X],[X]). checks(_,[X,Z],[X,Z]). checks(V,[R1,R2,R3|T],[R1|St]) :- number(R2),!, R21 in R2..V, checks(V,[R21,R3|T],St). checks(V,[R1,R2,R3|T],[R1|St]) :- checks(V,R2,R21),checks(V,[R21,R3|T],St).
还有更多测试 :-assert_are_equal(sums([[13,16,15,18,15,15],[14,1,8,9,7,9],[19,5,4,2,5,10],[13,1,7,9,10,3],[17,7,5,10,6,1],[15,9,8,2,8,3]],36),true). :-assert_are_equal(sums([[18,13,13,17,12,11],[17,2,6,10,5,10],[11,10,2,8,8,2],[12,6,10,8,8,7],[18,4,7,6,7,4],[20,5,9,2,3,10]],18),true). :-assert_are_equal(sums([[14,20,11,19,19,16],[11,10,7,4,9,6],[17,2,2,6,10,9],[15,9,2,1,4,1],[15,5,5,5,8,7],[14,2,8,6,10,7]],11),true). :-assert_are_equal(sums([[19383,10886,12777,16915,17793,18335,15386,10492,16649,11421],[12362,27,8690,59,7763,3926,540,3426,9172,5736],[15211,5368,2567,6429,5782,1530,2862,5123,4067,3135],[13929,9802,4022,3058,3069,8167,1393,8456,5011,8042],[16229,7373,4421,4919,3784,8537,5198,4324,8315,4370],[16413,3526,6091,8980,9956,1873,6862,9170,6996,7281],[12305,925,7084,6327,336,6505,846,1729,1313,5857],[16124,3895,9582,545,8814,3367,5434,364,4043,3750],[11087,6808,7276,7178,5788,3584,5403,2651,2754,2399],[19932,5060,9676,3368,7739,12,6226,8586,8094,7539]],79058),true). :-assert_are_equal(sums([[10795,10570,11434,10378,17467,16601,10097,12902,13317,10492],[16652,756,7301,280,4286,9441,3865,9689,8444,6619],[18440,4729,8031,8117,8097,5771,4481,675,709,8927],[14567,7856,9497,2353,4586,6965,5306,4683,6219,8624],[11528,2871,5732,8829,9503,19,8270,3368,9708,6715],[16340,8149,7796,723,2618,2245,2846,3451,2921,3555],[12379,7488,7764,8228,9841,2350,5193,1500,7034,7764],[10124,4914,6987,5856,3743,6491,2227,8365,9859,1936],[11432,2551,6437,9228,3275,5407,1474,6121,8858,4395],[16029,1237,8235,3793,5818,4428,6143,1011,5928,9529]],68900),true). :-assert_are_equal(sums([[18776,12404,14443,15763,14613,14538,18606,16840,12904,14818],[15128,688,7369,7917,9917,6996,3324,7743,9470,2183],[18490,5499,9772,6725,5644,5590,7505,8139,2954,9786],[17669,8082,8542,8464,197,9507,9355,8804,6348,8611],[13622,7828,9299,7343,5746,5568,4340,5422,3311,3810],[17605,1801,5661,3730,4878,1305,9320,8736,9444,8626],[18522,3465,6708,3416,8282,3258,2924,7637,2062,5624],[12600,2036,3452,1899,9379,5550,7468,71,973,7131],[13881,4930,8933,5894,8660,163,7199,7981,8899,2996],[12959,3773,2813,9668,7190,1095,2926,6466,5084,1340]],61413),true). :-assert_are_equal(sums([[12090,17684,13376,15542,15936,19107,17445,19756,19179,18418],[16887,9412,3348,2172,1659,2009,2336,5210,6342,7587],[18206,9301,7713,7372,5321,1255,4819,4599,7721,9904],[15939,9811,3940,5667,1705,6228,1127,9150,5984,6658],[13920,9224,2422,7269,1396,4081,5630,84,9292,1972],[17672,3850,7625,5385,1222,9299,6640,6042,3898,713],[12298,6190,524,2590,8209,8581,8819,9336,7732,1155],[15994,8004,379,4769,5273,1776,8850,7255,1860,8142],[15579,5884,1993,3205,7621,9567,2504,613,1961,2754],[11326,4259,8944,8202,3202,3506,6784,2021,2842,868]],89383),true). :-assert_are_equal(sums([[19528,15189,18872,19908,19958,10498,18036,18808,17753,16248],[13303,3333,2133,1648,2890,9754,7567,1746,368,9529],[14500,8046,3788,9797,6249,6990,3303,3033,5363,2497],[10253,4892,7686,9125,1152,3996,5975,9188,9157,3729],[15436,2460,3414,3921,460,6304,28,8027,8050,6748],[17556,8902,4794,7697,8699,1043,1039,2002,428,6403],[14500,681,7647,8538,6159,5151,2535,2134,4339,1692],[12215,6127,504,5629,49,964,8285,6429,5343,6335],[13177,2900,5238,7971,6949,289,5367,7988,2292,5795],[10743,3144,2829,8390,1682,5340,3541,569,3826,4232]],100439),true).
这些是现场测试,只有前30件。 结果非常好,问题得以解决,甚至可以一直持续到一秒钟。
您可以检查...
结论
声明式编程涉及任务的详细形式化,求解器将寻找满足条件的最有效解决方案。
对该主题进行更深入的介绍,您可以打开minizinc ,这是一种嵌入了该范例的编程语言。 他们提出了许多含义,表示了限制,然后回答。 他们解决数独 ,地图着色任务, 计划工作 ,资源问题,计划。 我建议训练...