大家好! 我叫Grisha,是CGDevs的创始人。 在开发游戏时,数学是一个非常酷的工具。 但是,如果我们说如果不了解
向量和
矩阵就很难进行管理,那么三角剖分算法并不是必需的,而是借助三角剖分算法可以解决很多有趣的问题。 今天,我想谈一谈计算几何中一个相当重要的工具,例如三角剖分及其在游戏行业中的应用。 此外,我为出色的Unity Triangle.Net库编写了端口和一些包装。 如果有兴趣-欢迎猫。 链接到附件的github。

什么是三角剖分?
在一般情况下,
三角剖分是将几何对象划分为三角形。 这个概念本身很简单。 在游戏引擎的情况下,三角剖分的基本示例是网格。 严格来说,网格不仅可以由三角形组成,而且在游戏引擎中由于多种原因,它是由三角形组成的网格。

三角剖分是不同的,但是最流行的三角
剖分类型之一是
Delaunay三角剖分。 这种三角剖分的特征在于,在围绕每个三角形的外接圆中,只有该三角形的顶点处于该位置。

为什么需要它们?
通常,在游戏行业之外,借助三角剖分可以解决大量任务。 在游戏开发人员中,想到的第一个任务是导航网格。 Navmesh是一种数据结构,它确定玩家可以行走的空间。 它避免了诸如确定与部分环境的碰撞之类的复杂计算任务。
在游戏开发中使用Delaunay三角剖分可以解决的第二个有趣问题是生成地形和以点集表示的对象。 在这种情况下,Delaunay三角剖分的主要优点是,基于其属性,它可以使您避免使用非常尖锐的三角形,这些三角形会干扰并在地形上产生伪影。

此外,使用受约束的Delaunay三角剖分和算法(例如Chew的第二种算法和Ruppert的算法),您可以为地形生成更好的网格,并为另一种应用(有限元方法)生成良好的网格。
有限元方法本身就是解决应用物理问题的方法之一。 在gamedev中,它可以解决与变形模拟,流体模拟以及其他特殊用途有关的许多问题。 效果。 通常用于在动画中记录效果,因为该方法对于实时而言具有太高的计算复杂性。 使用该方法时,一个重要的细节是该方法的误差取决于网格中三角形的角度。 如果网格中存在非常尖锐的角度,则该方法会产生很大的误差,因此需要上面列出的算法。
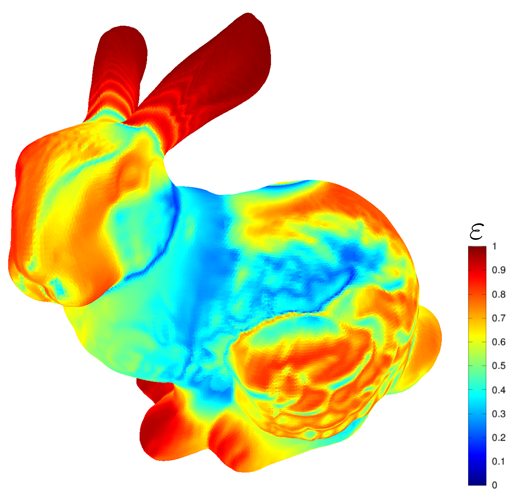
当然,一般来说,程序网格是生成的。 例如,一个github项目显示了一个具有绘制网格的功能的场景。 一些物理难题将这个应用程序用作基本机制。 但是此外,三角剖分算法允许使用过程生成来解决诸如过程可破坏性等问题。
除了gamedev三角剖分法还用于网络,计算机视觉,各种分析算法以及计算几何的哪些问题(例如相互组合和消除多边形)(通常在游戏开发中产生的问题中很有用)
带孔的耳朵夹

也许是最简单的三角剖分算法之一。 它没有给出最佳的网格,并且在最坏的情况下具有最大的计算复杂度O(n ^ 2)。
您可以在本文中阅读有关它的更多信息。Bowyer – Watson算法
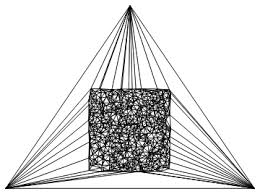
在一组点上生成Delaunay三角剖分的算法。 通常,与大多数Delaunay算法一样,如果正确实现,则算法复杂度为O(n log n),其中n是顶点数。 但在某些情况下,可能需要O(n ^ 2)。
关于削耳的缺点是该算法建立凸三角剖分,并且在基本实现中不涉及结果网格中的孔。
Delaunay优化处理
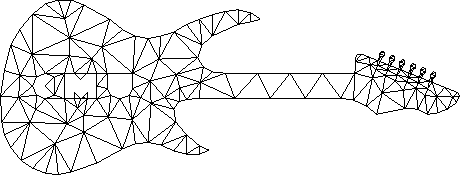
Chew的第二个算法和Ruppert的算法是允许您在Delaunay三角剖分中输入约束并设置网格中三角形的最小角度的算法。 算法的一个重要细节是它们可以进入无限循环,并保证以大约20.7度到29度之间的角度给出结果。 设置最小角度的能力对于解决上述问题很重要。
咀嚼的第二种算法在免费软件包
www.cs.cmu.edu/~quake/triangle.html中实现 ,其端口位于.Net
archive.codeplex.com/?p=triangleTriangle.Net for Unity
好吧,由于在三角剖分的帮助下您可以解决很多很酷的任务,所以在假期我想为Unity实现我的包装器,这样我总会拥有一个方便的工具。 在此实现中,三角剖分算法平均适用于O(n),在最坏的情况下适用于O(n * log n),其中n是顶点数。 例如,当测试随机散布在一个正方形上的1kk个顶点时,英特尔酷睿i7-8700上的编辑器中的单元平均花费7.56秒建立了一个网格。
与原始库的主要区别在于存在为Unity量身定制的扩展方法,以及在整个库中用float替换double(加上几个用于转换的特定运算符),在单元中没有太大意义。 如果我们考虑物理模拟,那么我将在plus库上使用单独的应用程序,并且计算结果已经完全提供给Unity以进行可视化。 并且还将Mesh类型重命名为TriangleNetMesh,以免相对于Unity中的Mesh产生干扰。 是的,它们已经在不同的命名空间中,但是,我认为新来者会因为在一个Mesh的帮助下获得另一个而感到沮丧。
该库的本质是必须首先指定所谓的多边形。 然后,基于它,已经生成了网格。 为了使其与单元数据结构一起使用,已引入了几种扩展方法。
使用范例public void GenerateMesh() { if(_CurrentState != MeshDrawerState.Nothing) return; Polygon poly = new Polygon(); poly.Add(_Contour); foreach (var hole in _Holes) { poly.Add(hole, true); } var triangleNetMesh = (TriangleNetMesh) poly.Triangulate(); GameObject go = new GameObject("Generated mesh"); var mf = go.AddComponent<MeshFilter>(); var mesh = triangleNetMesh.GenerateUnityMesh(); mesh.uv = GenerateUv(mesh.vertices); mf.mesh = mesh; var mr = go.AddComponent<MeshRenderer>(); mr.sharedMaterial = _MeshMaterial; var collider = go.AddComponent<PolygonCollider2D>(); collider.points = _Contour.ToArray(); var rb = go.AddComponent<Rigidbody2D>(); rb.mass = triangleNetMesh.Triangles.Sum(tris => tris.Area); Clear(); }
作为演示和使用示例,制作了一个特殊的演示场景,可以绘制网格。 您可以在
github项目中熟悉它和库的端口
。感谢您的关注! 我希望端口和文章对某人有用,并且这将使我们更加清楚为什么需要三角剖分和整个数学知识。 我将尝试继续公开解决游戏开发中各种数学问题的应用程序和方法。 在计算几何本身中,仍然有很多有趣的东西,但是除了高级数学之外,还有许多其他有趣的部分。