考虑预测时间序列。 让我们尝试预测报价图表或其他有用的信息。
让我们
以“最大相似度样本的时间序列预测模型 ”一文中提供的预测为基础
:说明和示例 (本文不是我的)。 简要点是,搜索过去历史记录中最左侧的图的最相似片段,然后从旧的最佳值中提取最右侧的值并将其用作预测。
我会走的更远。 在计算预测时,我不会选择相关性最好的一种情况,而是一堆最好的情况。 预测将是此数据包结果的平均值。 这将使您有可能了解发现的值是规律性的,而不是与所需预测的偶然巧合,如果预测偏离实际预测值,则不是随机偏差。
使用该文章中的单个最佳选项是不正确的,并且使用该分布中的一个值确定概率分布也不正确。 如果您生成一个非常大的随机数据图并开始搜索它们,那么它们中肯定会有相关的片段,甚至可能具有0.9999的系数,但是完全没有必要让相似的片段进一步跟随这些片段-仍然一切都是随机的。 而且,我们只需要打包一包这样的数据段,并计算出后续数据的方差低于这些数据的随机样本所形成的方差。 如果包装的分散性较低,那么这就是预测。 尽管这也不是可能的错误的准确表示,但到目前为止已经足够。
即
预测不是我们使用的抽样原则和所比较段的相关性,主要是因为应用此样本后,期望值的方差小于随机抽样的结果。
同样,此包的差异将使得可以评估使用以前案例中的选择选项哪个更好。 毕竟,可能不总是选择一个相关数据段,也不总是选择使用Pearson相关。 并且可以为每个预测点分别做出这样的选择。 对于哪种类型的样本,方差较小,对于当前点,该选项更好。
什么尺寸的包装应该是? 这取决于置信区间的问题。 为了不增加太多负载,有人提到最好至少使用30个示例来确定平均值。 如果测试数据过多,我将至少花费100。
为了与其他采样算法进行比较,或者为了确定这种预测的有用性,根据该算法的样本标准偏差与随机样本的标准偏差之比可以称为当前点预测算法成功的理论成功系数,而实际值尚不可用。
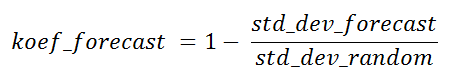
在某些情况下,该系数可能取负值。 发生这种情况的点以及系数为零的点都没有什么意义。 在100%可预测性的情况下,它将等于1。
让我们继续从该文章开始的实际示例。 在纠正了那里的小错误之后,我们得到了与该文章和该算法一致的以下结果:
2012年9月1日23:00时的预测的计算位置52631
检查相似性的总价值2184
最佳相关0.958174位置52295
传递系数alpha(1/2)1.03117 -11.1992
来自事实映射的预测误差5.210%mape-原始文章平均绝对百分比误差中的术语,由公式计算得出
Abs(预测-事实)/事实现在,让我们选择一个最佳的相似度,而不是最佳的相似度,并结合一切来预测某个时刻并观察会发生什么:
0 corr 0.958174 pos 52295映射5.210%
1 corr 0.953571 pos 52151映射6.566%
2 corr 0.953532 pos 45599 mape 11.642%
3 corr 0.951462 pos 45743映射7.033%
4 corr 0.950921 pos 45575映射3.300%
5 corr 0.950789 pos 38687映射3.538%
此处,相关值从值变为可忽略的值。 同时,预测结果的值从3%到11%不等。 即 最初的5%只是巧合,可能是11%和3%。
在该文章中指定的相似性条件下,总共可以比较2184个值。 其中,我从1500件中取了最好的一包,按相关性递减的顺序排序,并在图表中显示。 此包中的相关性从最佳0.958从左到右下降到0.715。 但是结果的波动实际上并没有改变:

可以看出,结果对相关性的依赖性很低,但是似乎仍然存在。 通常,我们从前100个值中提取一包,并按此包的平均值计算出预测值(如我所述)。 结果如下:
mape 5.824%,stddev mape 7.035% 。 但是,这个5.8%不再是巧合,而是分布的平均值-最有可能的预测。 映射标准偏差大于映射本身,但这是因为映射具有非对称分布。
我还计算了相同的预测,但是对于条件随机样本,更准确地说,从所有可能的选项中简单地求平均值,
mape结果
为8.246% 。 通过随机采样,误差会稍大一些,但该值仍在从最佳样本计算出的分散范围内。 对于计算的点,由me表示的理论预测系数接近于零,更确切地说,
koef_forecast = -0.041 。 我不是从stddev mape(它包括实际的预测)中计算出来的,而是从预测的绝对值中得出的,如果您查看该程序,则会在其中给出其原始编号。
但是,这与原始文章中提到的时间戳有关。 但是,如果我们说“ 9/4/2012 23:00”(月/日/年时间),则效率的理论系数为
koef_forecast = 0.21 ,mape = 3.126%,mape_rand = 7.147% 。 即 koef_forecast预先显示,当前点的计算将比上一个更准确。 该系数有用的本质在于,即使在获取实际数据之前,您也可以以某种方式评估结果,因为 实际数据不参与其中。 越高,越好。 我已经提到绝对预测点的系数为1。
您自己可以在Qt C ++的演示程序中看到所有这些数字的变化,在那里您可以选择包装的日期和大小:
github上的
源代码根据以下算法选择最佳值:
inline void OrdPack::add_value(double koef, int i_pos) { if (std::isfinite(koef)==false) return; if (koef <= 0.0) return; if (mmap_ord.size() < ma_count_for_pack) { if (mmap_ord.size()==0) mi_koef = koef; mi_koef = std::min(mi_koef, koef); mmap_ord.insert({-koef,i_pos}); } else if (koef > mi_koef) { mmap_ord.insert({-koef,i_pos}); while (mmap_ord.size() > ma_count_for_pack) mmap_ord.erase(--mmap_ord.end()); mi_koef = -(--mmap_ord.end())->first; } }
在此处发布整个源代码毫无意义,在此并不复杂,并带有注释。
mainwindow.cpp文件中MainWindow :: to_do_test()过程的
基础 。
现在,我将继续在下一部分中进行预测。
PS。 请就所有遗漏的内容是否清楚一事发表评论。 我已经为下一步的工作制定了一个大概的计划,但是有了您的意见,我会做得更好。