幸福理论。 统计是一无所知的科学方法

我继续让哈勃（Habr）的读者熟悉他的著作《幸福理论》（Theory of Happiness）中的章节，并附带“中庸之道的数学基础”。 这本尚未出版的流行科学书，非常非正式地讲述了数学如何使您以新的认识水平看待世界和人们的生活。 它适用于对科学感兴趣的人和对生活感兴趣的人。 而且由于我们的生活是复杂的，而且总体上是不可预测的，因此本书的重点主要放在概率论和数理统计上。 这里没有证明定理，也没有给出科学的基础知识，这绝不是教科书，而是所谓的娱乐科学。 但是，正是这种几乎好玩的方法，使我们得以发展直觉，为学生提供生动的实例来丰富讲座，最后向非数学家和我们的孩子解释我们在干科学中发现了如此有趣的东西。


本章涉及统计，天气甚至哲学。 不用担心，只需一点点。 在一个体面的社会中，再也没有其他可以用来聊天的东西。

数字在欺骗，特别是当我自己做时； 在这种情况下，归因于Disraeli的陈述是正确的：“谎言分为三种：谎言，公然谎言和统计数据。”
马克·吐温

我们计划在夏季多久去一次户外活动，在公园散步或野餐，然后雨水中断了我们的计划，将我们囚禁在房子里！ 而且，如果这种情况每个季节发生一次或两次，有时似乎天气跟随周末，一次又一次到达星期六或星期日！

澳大利亚研究人员发表了一篇相对较新的文章 ：“峰值温度的每周周期和城市热岛的强度。” 新闻媒体对她进行了采访，并用以下标题重印了结果： “你不认为！ 科学家发现，周末的天气确实比平日差。” 引用的论文提供了澳大利亚多个城市多年来温度和降水的统计数据，确实揭示了星期六和星期日某些小时的温度下降。 此后，给出了一种解释，该解释将当地天气与由于交通流量增加而造成的空气污染水平联系起来。 在此之前不久，在德国进行了类似的研究，得出了大致相同的结论。

同意，分数是非常微妙的效果。 抱怨期待已久的星期六天气不好，我们正在讨论一天是晴天还是下雨天，这种情况更容易记录，甚至在没有准确仪器的情况下也能记住。 我们将对这个主题进行自己的小型研究，并得到一个出色的结果：我们可以自信地说，我们不知道星期几和天气在堪察加半岛是否相关。 具有负面结果的研究通常不会落在杂志和新闻摘要上，但对您我来说，重要的是要了解我通常可以自信地对随机过程发表一些看法。 在这方面，负面结果并不比正面结果差。

捍卫统计数字

罪魁祸首归咎于统计学：谎言和操纵的可能性，最后是不可理解的事物。 但是我真的想恢复这方面的知识，以表明任务要完成的难度以及理解统计给出的答案的难度。

概率论使用分布或综合组合计算形式的随机变量的精确知识。 我再次强调，有可能对随机变量有准确的了解。 但是，如果我们无法获得这些确切的知识，而我们唯一可以掌握的就是观察呢？ 新药的开发者进行的测试数量有限，交通流控制系统的创建者仅在实际道路上进行一系列测量，社会学家具有调查结果，此外，他可以肯定的是，在回答一些问题时，受访者只是撒谎。

显然，一个观察结果根本没有任何结果。 二-多于零，三，四...一百...您需要多少次观察才能获得您可以在数学精度上确定的随机变量的任何知识？ 那将是什么样的知识呢？ 最有可能的是，它将以表格或直方图的形式出现，这使得可以评估随机变量的某些参数，这些参数称为统计信息（例如，域，平均值或方差，不对称性等）。 也许看直方图就能猜出分布的确切形状。 但是注意！ -所有观察结果本身都是随机变量！ 只要我们对分布没有准确的了解，所有观察结果都只能为我们提供随机过程的概率描述！ 这里对随机过程的随机描述仍然不会混淆，甚至不想故意混淆！

是什么使数理统计成为一门精确的科学？ 它的方法使我们能够在一个明显有限的框架内得出自己的无知，并给出一种可计算的置信度，即在此框架内我们的知识与事实相符。 这是一种可以推理未知随机变量的语言，因此推理是有意义的。 这种方法在哲学，心理学或社会学中非常有用，因为它们很容易进行冗长的推理和讨论，而没有任何希望获得积极知识尤其是证明的希望。 总而言之，有许多文献致力于称职的统计数据处理，因为它是医师，社会学家，经济学家，物理学家，心理学家的绝对必要的工具……总之，对于所有研究所谓“现实世界”的科学家而言，这与理想数学的不同之处仅在于我们对它的无知程度。

现在，再来看一下本章的题词，并意识到自然而然地拥有的统计数据被贬低为第三类谎言。 这不是宇宙卑鄙的主要定律！ 从物理到经济，我们所知的所有自然法则均基于数学模型及其属性，但在测量和观察过程中已通过统计方法对其进行了验证。 在日常生活中，我们的大脑进行概括，观察模式，隔离并识别重复的图像，这可能是人脑可以做的最好的事情。 这正是人工智能如今正在教授的内容。 但是头脑会保留自己的力量，倾向于从单个观察中得出结论，而不用担心这些结论的准确性或有效性。 在这种情况下，斯蒂芬·布拉斯特（Stephen Brast）的著作《伊索拉》（ Isola）中有一个很好的自洽声明： “每个人都从一个例子中得出一般性结论。 至少我只是这样做 。 ” 当我们谈论艺术，宠物的性质或讨论政治时，您不必为此担心很多。 但是，在建造飞机，组织机场派遣服务或测试新药时，您再也不能指称“在我看来”，“直觉告诉”和“生活中发生的一切”。 在这里，您必须将注意力集中在严格的数学方法的框架上。

我们的书不是教科书，我们不会详细研究统计方法，而只会局限于一件事-检验假设的技术。 但是，我想展示该知识领域的推理过程和结果形式。 而且，也许，一些读者，即未来的学生，不仅会理解为什么用所有这些QQ图，t和F分布来用统计数据折磨他，还会出现另一个重要的问题：如何知道什么？ -当然是出事了吗？ 使用统计数据，我们到底能学到什么？

统计三鲸

数理统计的主要支柱是概率论， 大数定律和中心极限定理 。

用自由解释的大数定律表明， 对随机变量的大量观察几乎可以肯定地反映了其分布 ，因此，观察到的统计量：平均值，方差和其他特征趋于精确对应于随机变量的值。 换句话说，具有无限数量的数据的观测值的直方图几乎可以肯定地倾向于我们可以认为是真实的分布。 正是这一定律将概率的“日常”频率解释与理论联系起来，作为概率空间中的度量。

中心极限定理再次以一种自由的解释说，随机变量分布的最可能形式之一是正态 （高斯）分布。 确切的措辞听起来有所不同： 大量相同分布的实数随机变量的平均值，无论其分布如何，均由正态分布描述。 这个定理通常是用泛函分析方法证明的，但是我们稍后将看到它可以通过引入熵的概念来理解甚至扩展，该熵是对系统状态概率的一种度量：正态分布的熵最大，约束数量最少。 从这个意义上讲，当描述一个未知的随机变量或一个随机变量是许多其他变量的组合时，它是最佳的，这些变量的分布也是未知的。

这两个定律是基于观察结果对我们的知识的可靠性进行定量估计的基础。 在这里，我们谈论的是假设的统计确认或反驳，这些假设可以从一些通用的基础和数学模型中得出。 这可能看起来很奇怪，但是统计数据本身并不能产生新的知识。 一组事实只有在形成某种结构的事实之间建立联系之后才变成知识。 正是这些结构和关系使我们能够基于统计之外的东西做出预测并做出一般假设。 这种假设称为假设 。 现在是时候回想一下眼神定律之一了， Persigue假设 ：

解释任何给定现象的合理假设的数量是无限的。

数理统计的任务是限制此无限数量，或者将其减少为一个，并且不一定完全正确。 为了转为更复杂（且通常更理想）的假设，有必要使用观察数据来驳斥更简单，更笼统的假设，或者强化它并放弃该理论的进一步发展。 经常以这种方式检验的假设称为null ，这具有深刻的意义。

什么可以作为原假设？ 从某种意义上讲，任何内容，任何陈述，但条件是可以将其翻译为度量语言。 大多数情况下，假设是某个参数的期望值，该期望值在测量过程中会变成随机变量，或者两个随机变量之间不存在联系（相关性）。 有时假定分布类型，随机过程和一些数学模型。 这个问题的经典表述如下：观察是否允许我们拒绝原假设？ 更确切地说，我们可以肯定地说，不能基于零假设获得观察结果吗？ 此外，如果我们无法基于统计数据证明原假设是假的，则将其视为真实。

在这里，您可能会认为研究人员被迫犯了经典的逻辑错误之一，该错误带有拉丁字母ad ignorantiam的son谐。 基于缺乏证伪的证据，这是对陈述真相的论证。 一个典型的例子是参议员约瑟夫·麦卡锡（Joseph McCarthy）被要求提供事实以支持他指责某人是共产主义者的言论 ： “我对这个问题知之甚少，除了主管当局的一般性声明，即他的档案中没有任何内容。排除他与共产党的联系 。 “ 甚至更聪明： “大脚怪存在，因为没有人证明过 。 ” 识别科学假设与类似技巧之间的差异是整个哲学领域的主题： 科学知识的方法论 。 其惊人的结果之一是可证伪性的标准，这是由杰出的哲学家卡尔·波普尔（Karl Popper）在20世纪上半叶提出的。 此标准旨在将科学知识与非科学知识区分开，乍看之下似乎很矛盾：

一个理论或假设只有在存在的情况下，甚至假设存在反驳的方法，才能被认为是科学的。

什么是卑鄙定律！ 事实证明，任何科学理论都自动会潜在地不正确，并且“按定义”是正确的理论不能被视为科学。 而且，诸如数学和逻辑学之类的科学不满足该标准。 但是，它们不是指自然科学，而是指形式科学，而后者不需要进行证伪性测试。 而且，如果我们同时增加一个结果：哥德尔的不完全性原则 ，该原则指出，在任何正式系统中都可以制定既不能证明也不可以反驳的声明，那么可能不清楚现在为什么要从事所有这些科学。 但是，重要的是要理解波普尔的可证伪性原则并没有说理论的真实性 ，而只是说它是否科学。 它可以帮助确定一种理论是否提供了一种有意义的语言来谈论世界。

但是，为什么，如果我们不能根据统计数据拒绝该假设，我们是否有权接受它呢？ 事实是，统计假设并非来自研究人员的意愿或偏好，它应遵循任何一般的正式法律。 例如，根据中央极限定理或最大熵原理。 这些法律正确地反映了我们的无知程度 ，而没有不必要地添加不必要的假设或假设。 从某种意义上讲，这是直接使用被称为奥卡姆剃刀的著名哲学原理的 ：

在更少的假设基础上可以做的事情不应该在更多的假设基础上做。

因此，当我们接受零假设时，由于没有反驳，我们正式和诚实地表明，作为实验的结果，我们的无知程度保持在同一水平 。 在大脚怪的例子中，明示或暗示地假设了相反的情况：缺乏证据表明这种神秘生物似乎并不能增加我们对其的了解程度。

通常，从可证伪性的原则来看，任何关于某物存在的陈述都是不科学的，因为缺乏证据不能证明任何东西。 同时，可以通过提供副本，间接证据或证明构造物的存在来轻松驳斥不存在任何东西的主张。 从这个意义上说，统计假设检验分析了没有达到预期效果的指控，从某种意义上说，可以提供对这一陈述的准确反驳。 这完全是“零假设”一词的正当理由：它包含有关系统的必要最低限​​度知识。

如何混淆统计数据以及如何解散

必须强调的是，如果统计数据表明可以拒绝原假设，这并不意味着我们由此证明了任何其他假设的真实性。统计学不应与逻辑相混淆，逻辑中应包含大量细微的错误，尤其是当相关事件的条件概率起作用时。例如：一个人不可能是教皇（$$〜1 / 7 BN）从此遵循教皇约翰·保罗二世是不是男人？这种说法似乎是荒谬的，但不幸的是，这样一个“显而易见的”结论同样是不正确的：该测试表明，对血液中酒精含量的移动式测试无法再$\sim 1/7$$$因此，假阳性和假阴性结果的 1 ％$1\%$$$在98 ％的情况下，他会正确识别出醉酒的驾驶员。让我们测试$98\%$$$1000个驱动程序让$1000$$$他们中有 100个真的会喝醉。结果，我们得到$100$$$900 × 1 ％= 9个假阳性和$900\times1\%=9$$$100 × 1 ％= 1个假阴性结果：也就是说，对于一个醉汉溜进去，将有9个无辜的随机驾驶者。什么是卑鄙定律！仅当醉酒司机的比例等于$100\times1\%=1$$$1 / 2，或者，如果假阳性和假阴性结果的分数的比率将是接近实际相对于清醒醉酒的司机。而且，对国家的调查越清醒，对我们描述的设备的使用就越不公平！在这里，我们面临着依赖事件。请记住，Kolmogorov对概率的定义是一种添加事件组合概率的方法：将两个事件组合的概率等于其概率之和减去相交的概率。但是，这些定义并未说明如何计算事件相交的概率。为此，引入了一个新概念：条件概率和事件之间的相互依赖关系成为首要问题。$1/2$


事件A和事件B的交集概率定义为事件B的概率与事件的概率的乘积 $$A，如果已知已发生事件$A$$$$B$ ：

$$

$$P(A \cap B) = P(B)P(A|B).$$

现在，您可以通过三种等效方式确定事件的独立性：事件 $$$A$ 和 $$B独立，如果$B$$$P （A | B ）= P （A ），或$P(A|B) = P(A)$$$P （B | A ）= P （B ），或$P(B|A) = P(B)$$$$P(A\cap B) = P(A)P(B)$ 。
这就完成了从第一章开始的概率的正式定义。

交叉口是可交换的运算，即$$$P(A\cap B) = P(B\cap A)$ 。 这立即意味着贝叶斯定理：

$$

$$P(A|B)P(B) = P(B|A)P(A),$$

可以用来计算条件概率。

在带有驾驶员和酒精测试的示例中，我们发生了以下事件：$$A-司机喝醉了，$A$$$B-测试给出阳性结果。机率：$B$$$P （A ）= 0.1-停车的驾驶员醉酒的概率；$P(A) = 0.1$$$P （B | A ）= 99 ％ -如果已知驾驶员喝醉了，则测试给出肯定结果的概率（排除在外）$P(B|A) = 99\%$$$1 ％假阴性）$1\%$$$P （A | B ）= 99 ％ -测试结果为阳性的测试醉酒的可能性（排除$P(A|B) = 99\%$$$1个假阳性结果）。我们计算$1%$$$$P（B）$ -在道路上获得正面测试结果的可能性：

$$

$$P（B）= \ frac {P（A）P（A | B）} {P（B | A）} = P（A）= 0.1$$

现在，我们的推理已经正式化，而且，正如您所知，也许对某些人来说更容易理解。 条件概率的概念使您可以使用概率论的语言进行逻辑推理。 不足为奇的是，贝叶斯定理在决策理论，模式识别系统，垃圾邮件过滤器，测试窃测试的程序以及许多其他信息技术中得到了广泛的应用。

医学检验或法律实践的学生会仔细理解这些示例。 但是，恐怕既没有向记者或政客传授数理统计也没有传授概率论，但他们急切地希望利用统计数据，自由地解释它们，并将获得的“知识”带给大众。 因此，我敦促读者：我自己弄清楚了数学，再帮我解决一下！ 我看不到其他无知的解毒剂。

我们衡量我们的信度

我们将仅考虑并在实践中应用众多统计方法中的一种：检验统计假设。 对于那些已经将生命与自然科学或社会科学联系起来的人来说，这些例子中不会出现令人惊讶的新事物。

假设我们重复测量具有平均值的随机变量 $$$\亩$ 和标准偏差 $$$\ sigma$ 。 根据中心极限定理，观测到的平均值将呈正态分布。 从大数定律得出，其平均值趋向于 $$$\亩$ ，从正态分布的属性可以得出 $$$n$ 测量时，观察到的平均值方差将随着 $$$\ sigma / \ sqrt {n}$ 。 标准偏差可以看作是平均测量的绝对误差，这种情况下的相对误差等于 $$$\ delta = \ sigma /（\ sqrt {n} \ mu）$ 。 这些是非常笼统的结论，与足够大无关 $$$n$ 从调查随机变量的特定分布形式中得出。 他们遵循两个有用的规则（不是法律）：

1.最少测试次数 $$$n$ 应该由所需的相对误差决定 $$$\ delta$ 。 而且，如果

$$

$$n \ geq \ left（\ frac {2 \ sigma} {\ mu \ delta} \ right）^ 2，$$

那么观察到的平均值将保持在指定误差范围内的概率至少为 $$$95 \％$ 。 在 $$$\亩$ 接近零时，相对误差最好替代绝对值。

2.假设为零假设，即观察到的均值为 $$$\亩$ 。 然后，如果观察到的平均值不超过 $$$\ mu \ pm 2 \ sigma / \ sqrt {n}$ ，则原假设为真的概率至少为 $$$95 \％$ 。


如果被这些规则取代 $$$2 \西格玛$ 在 $$$3 \西格玛$ ，则置信度将增加到 $$$99.7 \％$ 这是一个很强的规则 $$$3 \西格玛$ ，这在物理科学中将假设与实验确定的事实区分开来。

考虑将这些规则应用到伯努利分布中，描述一个随机变量，该变量正好具有给定成功概率的两个值（有条件地称为“成功”和“失败”），这对我们很有用。 $$$p$ 。 在这种情况下 $$$\亩= p$ 和 $$$\ sigma = \ sqrt {p（1-p）}$ ，因此对于所需的实验次数和置信区间，我们得到

$$

$$n \ geq \ frac {4} {\ delta ^ 2} \ frac {1-p} {p} \ quad和\ quad np \ pm 2 \ sqrt {np（1-p）}$$

规则 $$$2 \西格玛$ 绘制直方图时，可以使用伯努利分布来确定置信区间。 本质上，直方图的每个条形图代表一个具有两个值的随机变量：“命中”-“缺失”，其中命中的概率对应于模拟的概率函数。 作为演示，我们将为均匀分布，几何分布和正态分布的三种分布生成许多样本，然后将观察到的数据的散布估计值与观察到的散布进行比较。 在这里，我们再次看到中心极限定理的回声，这一事实体现在直方图中平均值附近的数据分布接近正态这一事实。 但是，接近零时，扩散变得不对称，并接近另一个非常可能的分布-指数分布。 这个例子很好地说明了我的意思：在统计中，我们正在处理随机变量参数的随机值。


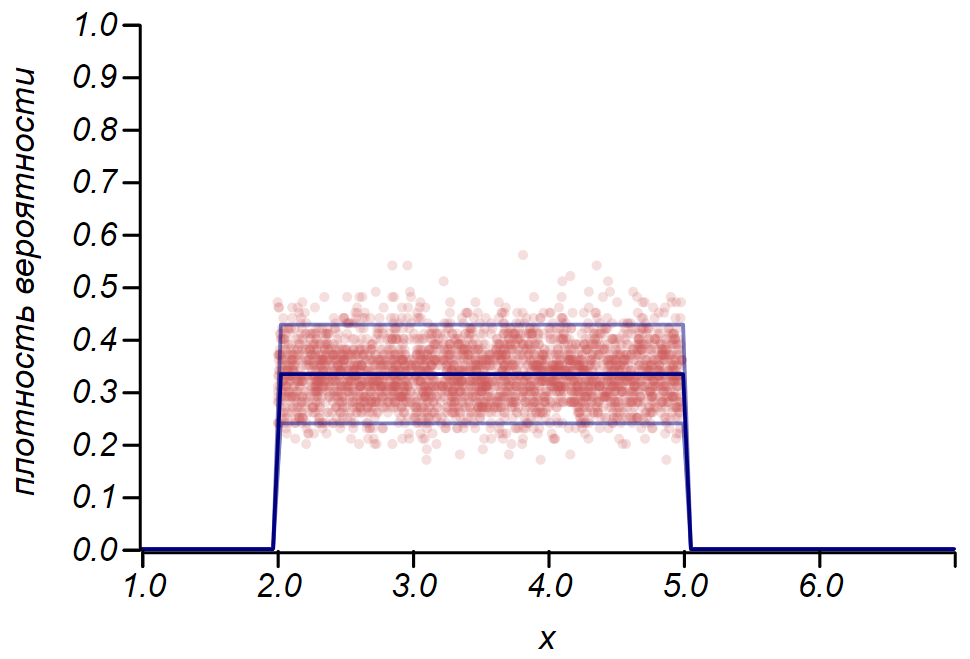
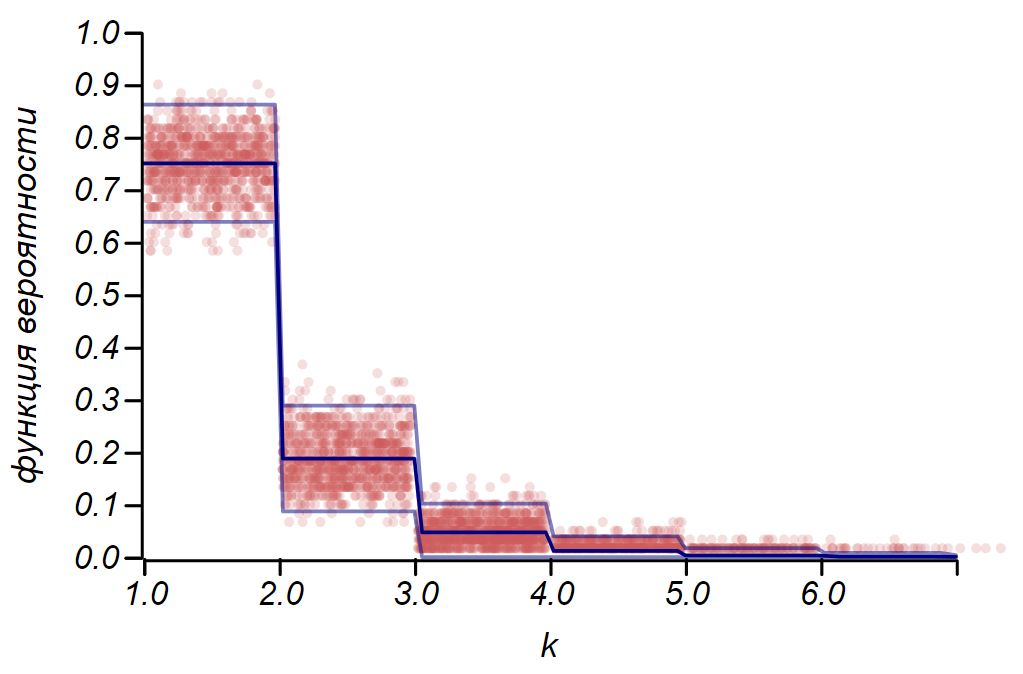显示由规则做出的分散估计的比率的示例 $$$2 \西格玛$ 以及三个随机变量的观察到的价差。

重要的是要了解规则 $$$2 \西格玛$ 甚至 $$$3 \西格玛$ 不要让我们免于犯错。 他们不保证任何陈述的真实性，也不是证据。 统计数据限制了对假设的不信任程度，仅此而已。

数学家和概率论精品课程的作者吉安·卡洛·罗塔（Gian Carlo Rota）在麻省理工学院的演讲中举了一个例子。 想象一下一本科学杂志，其编辑做出了一个坚定的决定：只接受发表具有符合规则的积极成果的文章，以供出版 $$$2 \西格玛$ 或更严格。 同时，社论栏指出读者可以肯定 $$$95 \％$ 读者不会在该杂志的页面上找到错误的结果！ statement，此说法很容易被导致酒后驾车时我们公然不公的相同推理所驳斥。 让 $$$1000$ 研究人员经验丰富 $$$1000$ 假设，其中只有一部分是真实的，例如， $$$10 \％$ 。 根据假设检验的含义，我们可以预期 $$ 错误的假设不会被错误地拒绝，并将与 $$$100 \倍0.95 = 95$ 真实的结果。 总计 $$$130$ 一个好的三分之一将是错误的！

这个例子很好地说明了我们的国内卑鄙定律，尚未被纳入人类学选集-切尔诺木丁定律中 ：

我们想要最好的，但结果还是一如既往。

假设正确假设的份额为，则很容易获得将包含在期刊中的错误结果百分比的一般估计。 $$$0 <\ alpha <1$ 并且接受错误假设的概率等于 $$$p$ ：

$$

$$x = \ frac {（1- \ alpha）p} {\ alpha（1-p）+（1- \ alpha）p}$$

该图显示了限制可以在日记帐中发布的故意不正确结果所占份额的区域。

当采用各种检验假设的标准时，估计包含明显不正确结果的出版物的百分比。 可以看出，按规则接受假设 $$$2 \西格玛$ 可能有风险，而标准 $$$4 \西格玛$ 已经可以认为是非常强大的。

当然我们不知道这一点。 $$$\ alpha$ ，而且我们永远都不会知道，但是它肯定还不够统一，这意味着，无论如何，社论栏的发言都不能被认真对待。 您可以限制自己严格的标准 $$$4 \西格玛$ 但它需要进行大量测试。 因此，有必要在一组可能的假设中增加真实假设的份额。 科学认知方法的标准方法就是针对这一点的：假设的逻辑一致性，与事实和理论的一致性，证明了它们的适用性，对数学模型和批判性思维的依赖。

再说一下天气

在本章的开头，我们谈到了这样一个事实，即周末和恶劣天气比我们想要的更多。 让我们尝试完成这项研究。 每个下雨天都可以看作是对随机变量的观察-一周中的某天有概率服从伯努利分布 $$$1/7$ 。 作为零假设，让我们假设一个星期的所有天在天气和降雨方面都是相同的假设可以使它们中的任何一个都下雨的可能性相同。 我们有两天的假期，所以我们得到了糟糕的一天与一天的假期相等的同时发生的预期概率 $$$2/7$ ，该值将成为伯努利分布参数。 多久下雨一次？ 当然，在一年的不同时间，以不同的方式，但是在彼得罗巴甫洛夫斯克-堪察加州，一年平均有90个雨天或下雪天。 因此，有降水的日子流强度约为 $$$90/365 \大约1/4$ 。 让我们计算一下我们应该注册多少个下雨的周末，以确保有某种模式。 结果显示在表中。

观察期	夏天	年份	$$$5$ 岁月
预期观察数	$$$23$	$$$90$	$$$456$
预期的阳性结果数	$$$6$	$$$26$	$$$130$
重大偏差	$$$4$	$$$9$	$$$19$
不良比例很大 总休假天数	$$$42 \％$	$$$33 \％$	$$$29 \％$

这些数字在说什么？ 如果在您看来，连续一年没有“夏天”，那邪恶的石头正通过向他们下雨来追赶您的周末，那么可以检查并确认。 但是，在夏季，只有在所有周末的五分之二以上都下雨的情况下，才能捕获恶石。 零假设表明，只有四分之一的周末应该与恶劣的天气相吻合。 在五年的观察中，人们已经可以希望注意到细微的偏差 $$$5 \％$ 并在必要时继续进行解释。

我利用了2014年至2018年的学校天气日记，了解了这五年来发生的情况 $$$459$ 他们的雨天 $$$141$ 落在周末。 实际上，这比预期的数量要多 $$$11$ 天，但重大偏差始于 $$$19$ 天，就像我们在童年时代所说的那样：“不算数”。 这是一系列数据和直方图，显示了一周中各天的恶劣天气分布。 直方图中的水平线表示对于相同数量的数据可以观察到的均匀分布随机偏差的间隔。


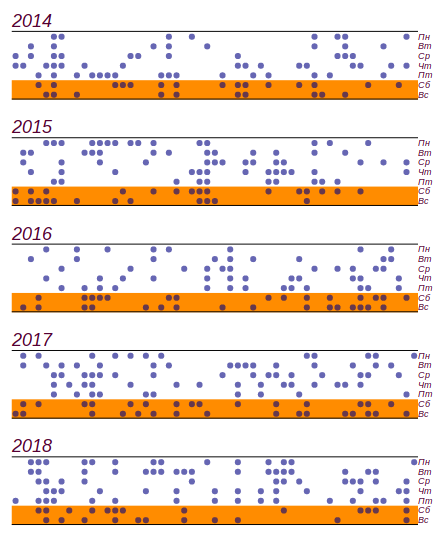
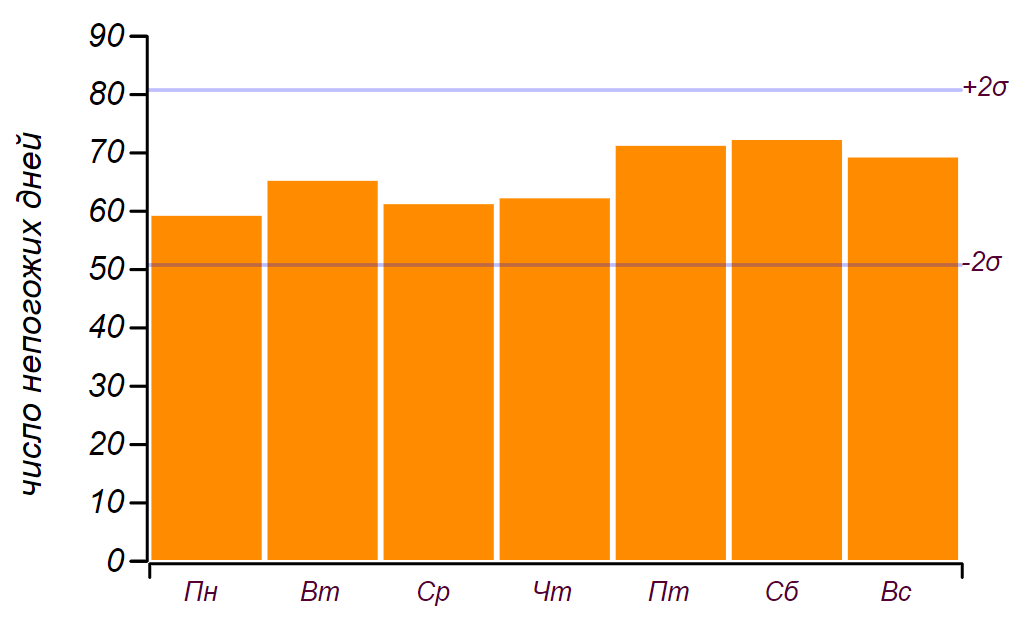经过五年的观察，获得了最初的一系列数据以及按星期几划分的不良天数分布。

可以看出，实际上自星期五以来，天气恶劣的天数增加了。 但是前提条件还不足以找到这种增长的原因：只需对随机数进行排序即可获得相同的结果。 结论：在观察天气的五年中，我积累了近2000条记录，但是到了星期几，我并没有学到任何有关天气分布的新知识。

当您查看日记条目时，很明显天气并不单单出现，而是两到三天甚至每周的飓风。 这会以某种方式影响结果吗？ 您可以尝试将此观测因素考虑在内，并假设平均下雨两天（实际上， $$$1.7$ 天），则阻止周末的可能性增加到 $$$3/7$ 。 在这种可能性下，五年的预期比赛次数应为 $$$195 \ pm21$ ，即来自 $$$174$ 之前 $$$216$ 次。 观察值 $$$141$ 不会落在这个范围内，因此，可以可靠地否定恶劣天气连续两天的影响这一假设。 我们学到新东西了吗？ 是的，我们了解到：该过程的明显特征似乎没有任何效果。 这是值得考虑的，我们稍后会做。 但是主要结论是，没有理由考虑任何更细微的影响，因为观察结果（最重要的是观察结果的数目）始终代表最简单的解释。

但是我们不满意的不是五年甚至每年的统计数据，人类的记忆时间并不长。 周末连续下雨三四次，真是太可惜了！ 多久可以观察到一次？ 特别是如果您还记得，并非只有恶劣的天气来临。 该任务可以表述为：“ $$$n$ 周末连续会​​下雨吗？” 可以合理地假设恶劣天气形成了强度较大的泊松流 $$$1/4$ 。 这意味着平均而言，任何时期的四分之一天都是不好的。 仅观察周末，我们不应该改变流量的强度，而在所有周末中，恶劣天气平均也应为四分之一。 因此，我们提出了零假设：风暴是泊松，具有已知参数，这意味着泊松事件之间的间隔由指数分布来描述。 我们对离散间隔感兴趣： $$$0，\ 1，\ 2，\ 3$ 天等，因此我们可以使用指数分布的离散模拟-参数的几何分布 $$$1/4$ 。 该图显示了我们所做的事情，可以看出我们正在观察泊松过程的假设是不合理的。


观察到的失败的周末和理论上的链条长度分布。 细线显示了我们拥有的观测数量的允许偏差。

您可以问自己一个问题：您需要观察多少年才能观察到 $$$11$ 天是否可以确定地确认或拒绝为随机偏差？ 很容易计算：观察到的概率 $$$141/459 = 0.307$ 与预期不同 $$$2/7 = $ 0.28$ 在 $$$0.02$ 。 要记录百分之一百的差异，绝对误差不超过 $$$0.005$ 这使得 $$$1.75 \％$ 从测量的大小。 从这里我们得到所需的样本量 $$$n \ geq（4 \ cdot 5/7）/（0.0175 ^ 2 \ cdot 2/7）\约32000$ 下雨天。 大约需要 $$$4 \ cdot 32000/365 \约360$ 多年的连续气象观测，因为只有第四天下雨或下雪。 las，这比堪察加加入俄罗斯的时间还多，所以我没有机会了解事情的“真实”情况。 特别是如果您考虑到在这段时间里气候已经发生了巨大变化-从小冰河时代开始，自然就处于下一个最佳状态。

那么澳大利亚研究人员如何设法以度为单位记录温度偏差，为什么考虑这项研究才有意义呢？ 事实是，他们使用的小时温度数据没有通过任何随机过程“变稀”。 所以超越 $$$30$ 多年的气象观测已经积累了超过百万分之一的读数，这降低了平均值的标准偏差 $$$500$ 相对于标准每日温度偏差的次数。 这足以谈论十分之一度的准确性。 此外，作者还使用了另一种精美的方法来确认时间周期的存在：时间序列的随机混合。 这种混合保留了统计特性，例如流动强度，但是，它“擦除”了时间模式，使过程真正成为了泊松。 通过对许多合成系列和实验系列的比较，我们可以验证所观察到的过程与泊松的偏差是否显着。 同样，地震学家A. A.古塞夫（A. A. Gusev） 表明 ，任何地区的地震都形成一种具有聚类性质的自相似流。 这意味着地震往往会及时聚集，形成非常不愉快的流动密封。 后来发现，大型火山喷发序列具有相同的性质。

随机性的另一个来源

当然，天气就像地震一样，无法通过泊松过程来描述-这些是动态过程，其中当前状态是先前状态的函数。 为什么我们每周的天气观测偏向于简单的随机模型？ 事实是，我们在七个模的推导系统上显示了七天的降水形成的规律过程，或者说数学语言。 这种投影过程能够从井井有条的一系列数据中产生混乱。 例如，从此处开始，大多数实数的十进制表示形式的数字序列中存在可见的随机性。

我们已经讨论过有理数，以整数分数表示。 它们具有内部结构，由两个数字确定：分子和分母。 但是，当以十进制形式编写时，您可以观察到诸如 $$$1/2 = 0.5 \上线{0}$ 或 $$$1/3 =0。\上划线{3}$ 定期重复已经相当随机的序列，例如 $$$1/17 =0。\上划线{0588235294117647}$ 。 无理数没有有限或周期性的十进制表示法，在这种情况下，混乱最常出现在数字序列中。 但这并不意味着这些数字没有顺序！ 例如，数学家遇到的第一个无理数 $$$\ sqrt {2}$ 以十进制表示法会生成一组随机数字。 但是，另一方面，该数字可以表示为无限的连续分数：

$$

$$\ sqrt {2} = 1 + \ frac {1} {2+ \ frac {1} {2+ \ frac {1} {2+ ...}}}。$$

通过求解方程式，很容易表明该链确实等于两个的根：

$$

$$x-1 = \ frac {1} {2+（x-1）}。$$

带有重复系数的连续分数很快就会被写入，例如周期性的十进制分数，例如： $$$\ sqrt {2} = [1，\ bar {2}]$ ， $$$\ sqrt {3} = [1，\上线{1,2}]$ 。 在这种意义上，著名的黄金分割率是最简单排列的无理数： $$$\ varphi = [1，\ bar {1}]$ 。 所有有理数都以有限的连续分数形式表示，有些形式是无理的-以无穷但周期性的形式表示，它们称为代数 ，即使在这种形式下也没有有限的记号- 先验的 。 先验中最著名的是数字 $$$\ pi$ ，它会以十进制形式和连续分数形式产生混乱： $$$\ pi \大约[3，7,15,1,292,1,1,1,2,1,3,1,14,2,1，...]$ 。 这是欧拉数 $$$e$ 剩余的先验（以连续分数的形式）显示隐藏在十进制表示法中的内部结构： $$$e \大约[2,1,2,1,1,4,1,1,6,1,1,8,1,1,10，...]$ 。

从毕达哥拉斯开始，也许没有一个数学家怀疑世界的狡猾，发现了需要的东西，如此基本的数字 $$ p i具有这种难以捉摸的复杂混沌结构。当然，它可以表示为相当优雅的数字系列的总和，但是这些系列并未直接说明该数字的性质，并且它们不是通用的。我相信，未来的数学家将发现一些新的数字表示形式，作为连续分数的通用形式，这将揭示数字本质所隐藏的严格顺序。$\ pi$

$$

$$*\ *\ *$$

本章的结果在大多数情况下是负面的。作为一个想用隐藏的模式和意外的发现使读者惊讶的作者，我怀疑它是否应该包含在本书中。但是我们关于天气的讨论变成了一个非常重要的话题-自然科学方法的价值和意义。

一个聪明的女孩，索尼娅·莎塔洛娃（Sonya Shatalova），在十岁的时候就通过孤独症的视角看待世界，给出了一个非常简洁而精确的定义：“科学是基于怀疑的知识体系”。现实世界是不稳定的，它力图掩盖测量的复杂性，可见的随机性和不可靠性。对自然科学的怀疑是不可避免的。数学似乎是确定性的领域，似乎可以忘记疑问。隐藏在这个王国的城墙后面是很诱人的。考虑可以彻底研究的无法识别的世界模型；计算，公式的好处就可以消化任何东西。但是，尽管如此，数学是一门科学，并且怀疑它是一种深层的内在诚实，在清除了数学构造中的其他假设和不必要的假设之后，数学才得以解决。在数学领域，他们说的是一种复杂但和谐的语言，适合于对现实世界进行推理。一定要熟悉这种语言非常重要，为了防止人物冒充统计数字，不允许事实假装成知识，而让无知和操纵与真实科学形成对比。