大家好! 我叫Grisha,是CGDevs的创始人。 让我们继续谈论数学之类的东西。 通常,数学在游戏开发和计算机图形学中的主要应用是VFX。 因此,让我们讨论一下这样一种影响-降雨,或者说是其主要部分需要数学计算-表面上的涟漪。 连续编写用于表面波纹的着色器,并分析其数学运算。 如果有兴趣-欢迎猫。 Github项目已附上。

有时,生活中会有片刻的时刻,程序员不得不抓住小手鼓并呼吁下雨。 通常,降雨建模本身的主题很深。 在此过程的不同部分上有许多数学著作,从滴状液滴及其相关影响到液滴的体积分布。 我们将仅分析一个方面-着色器,该着色器将使我们能够创建与滴落的波浪相似的效果。 现在该做手鼓了!
数学波在Internet上搜索时,会发现很多有趣的数学表达式,它们会产生波动。 通常,它们由某种“魔术”数和周期函数组成,没有理由。 但是总的来说,这种影响的数学非常简单。
在一维情况下,我们只需要一个平面波方程。 为什么我们稍后再分析平面和一维。
在我们的情况下
,平面波方程可以写成:
Aresult = A * cos(2 * PI *(x / waveLength-t *频率));其中:
结果 -时间点x处的振幅
A是最大振幅
波长 -波长
频率 -波动频率
PI -
PI编号= 3.14159(浮点)
着色器让我们玩一下着色器。 对于“ top”将负责坐标-Z。 在Unity中的2D情况下,这更加方便。 如果需要,着色器将不难重写为Y。
我们需要的第一件事是圆的方程。 我们的着色器的波将关于中心对称。 在2d情况下的圆方程描述为:
r ^ 2 = x ^ 2 + y ^ 2我们需要一个半径,所以等式采用以下形式:
r = sqrt(x ^ 2 + y ^ 2)这将使我们对网格中的点(0,0)具有对称性,这将使一切都简化为平面波的一维情况。
现在让我们编写一个着色器。 我不会分析编写着色器的每个步骤,因为这不是本文的目的,而是基于Unity的Standard Surface Shader,其模板可以通过Create-> Shader-> StandardSurfaceShader获得。
另外,
添加了波动方程所需的属性:
_Frequency ,
_WaveLength和
_WaveHeight 。 属性
_Timer (可以在hcp中使用时间,但是在开发和随后的动画制作过程中,手动控制它更方便。
我们编写getHeight函数以通过将波动方程替换为波动方程来获取高度(现在是Z坐标)
通过使用我们的波动方程和圆方程编写着色器,可以得到这种效果。
着色器代码Shader "CGDevs/Rain/RainRipple" { Properties { _WaveHeight("Wave Height", float) = 1 _WaveLength("Wave Length", float) = 1 _Frequency("Frequency", float) = 1 _Timer("Timer", Range(0,1)) = 0 _Color ("Color", Color) = (1,1,1,1) _MainTex ("Albedo (RGB)", 2D) = "white" {} _Glossiness ("Smoothness", Range(0,1)) = 0 _Metallic ("Metallic", Range(0,1)) = 0.0 } SubShader { Tags { "RenderType"= "Opaque" } LOD 200 CGPROGRAM #pragma surface surf Standard fullforwardshadows vertex:vert #pragma target 3.0 sampler2D _MainTex; struct Input { float2 uv_MainTex; }; half _Glossiness, _Metallic, _Frequency, _Timer, _WaveLength, _WaveHeight; fixed4 _Color; half getHeight(half x, half y) { const float PI = 3.14159; half rad = sqrt(x * x + y * y); half wavefunc = _WaveHeight * cos(2 * PI * (_Frequency * _Timer - rad / _WaveLength)); return wavefunc; } void vert (inout appdata_full v) { v.vertex.z -= getHeight(v.vertex.x, v.vertex.y); } void surf (Input IN, inout SurfaceOutputStandard o) { fixed4 c = tex2D (_MainTex, IN.uv_MainTex) * _Color; o.Albedo = c.rgb; o.Metallic = _Metallic; o.Smoothness = _Glossiness; o.Alpha = _Color.a; } ENDCG } FallBack "Diffuse" }
有海浪。 但是我希望动画以平面开始和结束。 正弦函数将对此提供帮助。 将振幅乘以sin(_Timer * PI),我们得到了平滑的波形出现和消失。 由于_Timer的取值范围是0到1,并且PI中的正弦值为零,因此正好是您所需要的。
虽然一点也不像一滴水落下。 问题在于波能会均匀丢失。 添加_Radius属性,该属性将负责效果的半径。 然后,我们将钳位幅度(_Radius-rad,0,1)相乘,已经获得了更像真相的效果。
好,最后一步。 每个点处的振幅在等于0.5的时间达到最大值的事实并不完全正确,最好替换此函数。

然后我感到有点懒惰,无法计数,我将正弦乘以(1-_Timer)并得到了这样的曲线。
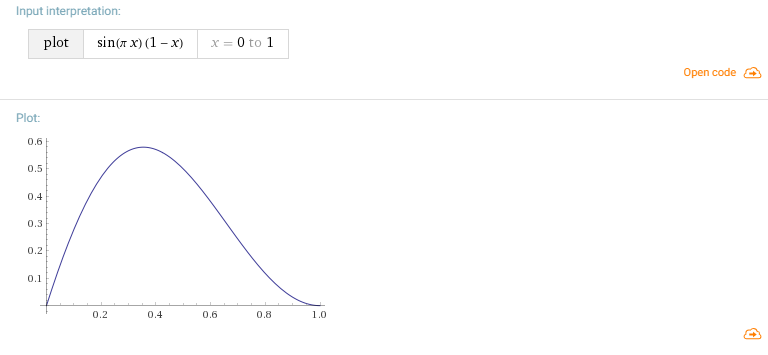
但是通常,从数学的角度来看,您还可以基于逻辑在想要峰值和近似形状的时间点上选择所需的曲线,然后在这些点上进行内插。
结果就是这样的着色器和效果。
着色器代码 Shader "CGDevs/Rain/RainRipple" { Properties { _WaveHeight("Wave Height", float) = 1 _WaveLength("Wave Length", float) = 1 _Frequency("Frequency", float) = 1 _Radius("Radius", float) = 1 _Timer("Timer", Range(0,1)) = 0 _Color ("Color", Color) = (1,1,1,1) _MainTex ("Albedo (RGB)", 2D) = "white" {} _Glossiness ("Smoothness", Range(0,1)) = 0 _Metallic ("Metallic", Range(0,1)) = 0.0 } SubShader { Tags { "RenderType"= "Opaque" } LOD 200 CGPROGRAM #pragma surface surf Standard fullforwardshadows vertex:vert #pragma target 3.0 sampler2D _MainTex; struct Input { float2 uv_MainTex; }; half _Glossiness, _Metallic, _Frequency, _Timer, _WaveLength, _WaveHeight, _Radius; fixed4 _Color; half getHeight(half x, half y) { const float PI = 3.14159; half rad = sqrt(x * x + y * y); half wavefunc = _WaveHeight * sin(_Timer * PI) * (1 - _Timer) * clamp(_Radius - rad, 0, 1) * cos(2 * PI * (_Frequency * _Timer - rad / _WaveLength)); return wavefunc; } void vert (inout appdata_full v) { v.vertex.z -= getHeight(v.vertex.x, v.vertex.y); } void surf (Input IN, inout SurfaceOutputStandard o) { fixed4 c = tex2D (_MainTex, IN.uv_MainTex) * _Color; o.Albedo = c.rgb; o.Metallic = _Metallic; o.Smoothness = _Glossiness; o.Alpha = _Color.a; } ENDCG } FallBack "Diffuse" }
网格物体很重要回到
上一篇文章的主题。 波是由顶点着色器实现的,因此网格的网格起着相当大的作用。 由于运动的本质是已知的,因此简化了任务,但总的来说,最终的视觉效果取决于网格的形状。 对于高多边形,该差异变得微不足道,但是对于性能而言,多边形越少越好。 下面的图片说明了网格和视觉效果之间的区别。
正确地: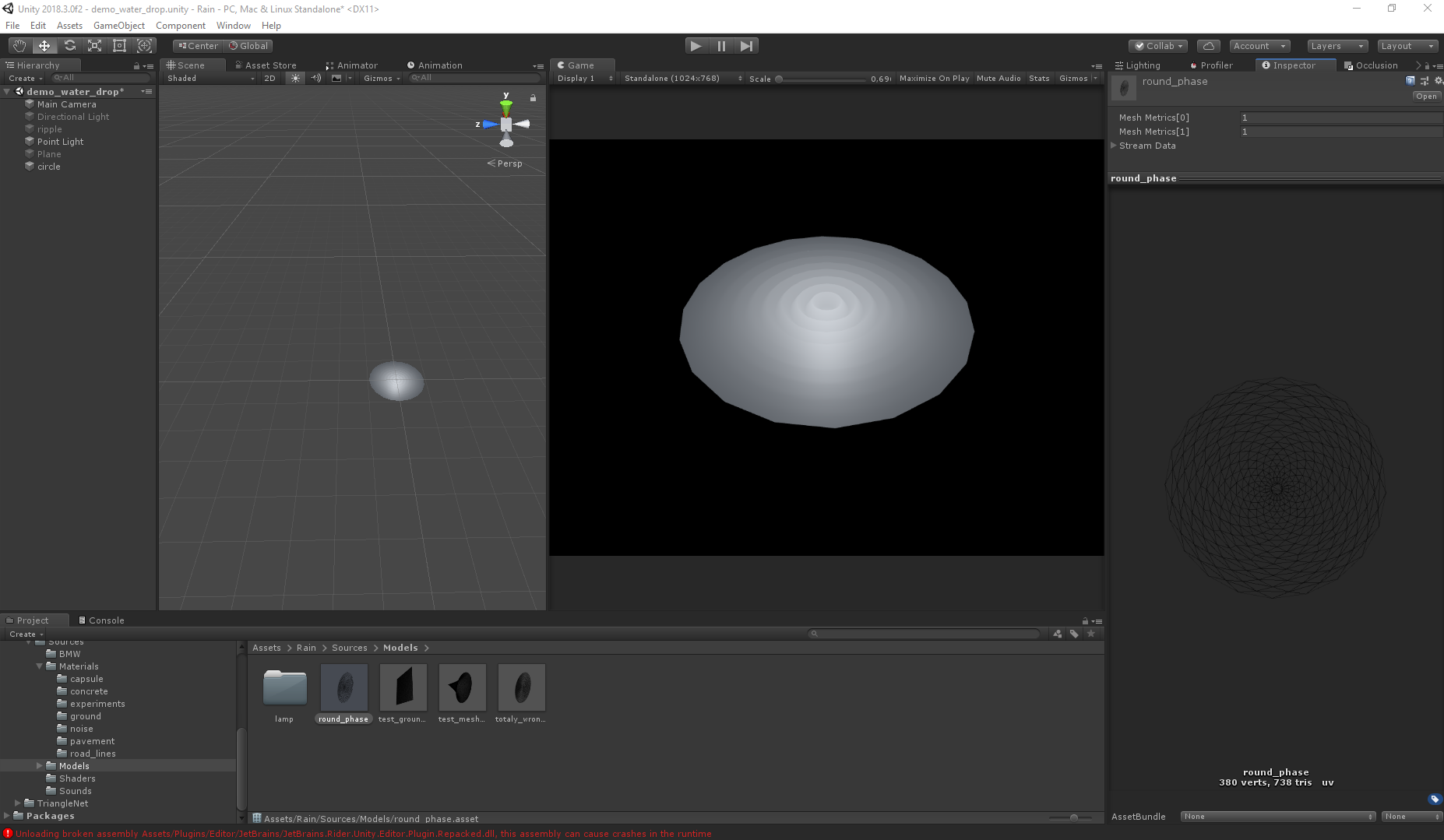 错误:
错误: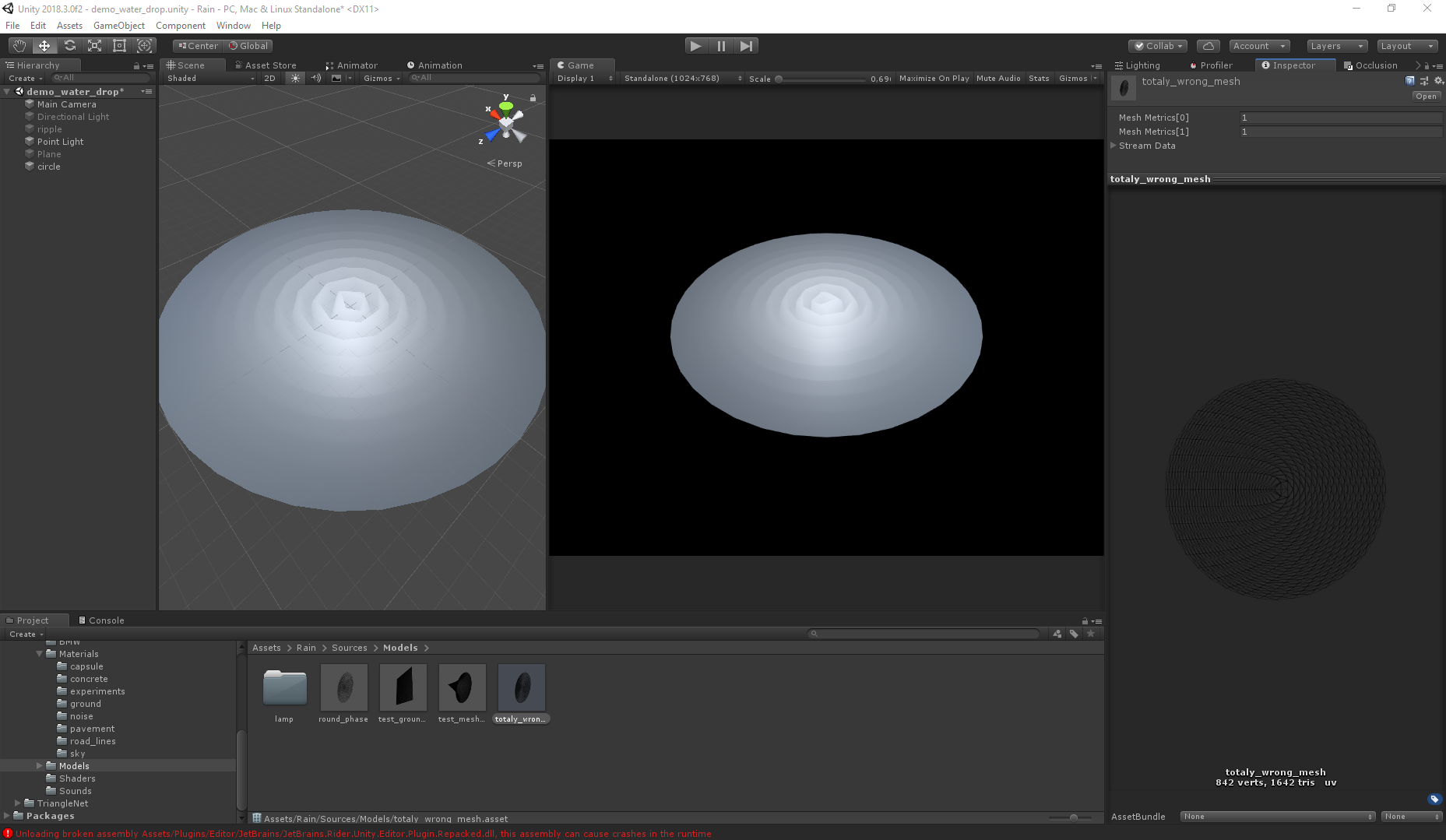
即使多边形的数量是原来的两倍,第二个网格也会产生错误的视觉效果(两个网格都是使用Triangle.Net生成的,只是使用了不同的算法)。
最终视觉在不同版本的着色器中,添加了一个特殊部分以创建严格地不在中心而是在多个点处的波浪。 如果该主题很有趣,我将在以下文章中介绍如何实现此方法以及如何传递此类参数。
这是着色器本身:
带极点的波纹顶点 Shader "CGDevs/Rain/Ripple Vertex with Pole" { Properties { _MainTex ("Albedo (RGB)", 2D) = "white" {} _Normal ("Bump Map", 2D) = "white" {} _Roughness ("Metallic", 2D) = "white" {} _Occlusion ("Occlusion", 2D) = "white" {} _PoleTexture("PoleTexture", 2D) = "white" {} _Color ("Color", Color) = (1,1,1,1) _Glossiness ("Smoothness", Range(0,1)) = 0 _WaveMaxHeight("Wave Max Height", float) = 1 _WaveMaxLength("Wave Length", float) = 1 _Frequency("Frequency", float) = 1 _Timer("Timer", Range(0,1)) = 0 } SubShader { Tags { "IgnoreProjector" = "True" "RenderType" = "Opaque"} LOD 200 CGPROGRAM #pragma surface surf Standard fullforwardshadows vertex:vert #pragma target 3.0 sampler2D _PoleTexture, _MainTex, _Normal, _Roughness, _Occlusion; half _Glossiness, _WaveMaxHeight, _Frequency, _Timer, _WaveMaxLength, _RefractionK; fixed4 _Color; struct Input { float2 uv_MainTex; }; half getHeight(half x, half y, half offetX, half offetY, half radius, half phase) { const float PI = 3.14159; half timer = _Timer + phase; half rad = sqrt((x - offetX) * (x - offetX) + (y - offetY) * (y - offetY)); half A = _WaveMaxHeight * sin(_Timer * PI) * (1 - _Timer) * (1 - timer) * radius; half wavefunc = cos(2 * PI * (_Frequency * timer - rad / _WaveMaxLength)); return A * wavefunc; } void vert (inout appdata_full v) { float4 poleParams = tex2Dlod (_PoleTexture, float4(v.texcoord.xy, 0, 0)); v.vertex.z += getHeight(v.vertex.x, v.vertex.y, (poleParams.r - 0.5) * 2, (poleParams.g - 0.5) * 2, poleParams.b , poleParams.a); } void surf (Input IN, inout SurfaceOutputStandard o) { o.Albedo = tex2D(_MainTex, IN.uv_MainTex).rgb * _Color.rgb; o.Normal = UnpackNormal(tex2D(_Normal, IN.uv_MainTex)); o.Metallic = tex2D(_Roughness, IN.uv_MainTex).rgb; o.Occlusion = tex2D(_Occlusion, IN.uv_MainTex).rgb; o.Smoothness = _Glossiness; o.Alpha = _Color.a; } ENDCG } FallBack "Diffuse" }
整个项目及其运作方式可在
此处找到。 的确,由于github(hdr skybox和car)的重量限制,必须删除部分资源。
感谢您的关注! 我希望这篇文章对某人有用,并且对于为什么需要三角学,分析几何学(与曲线有关的所有事物)和其他数学学科变得更加清楚。