金属搜索和神经网络

脉冲金属探测器的工作原理
构造金属搜索设备的热门选择之一是脉冲（ 感应 ）金属探测器-一种朴实而可靠的设备（良好的探测深度，对土壤矿化的抵抗力强，在盐水中工作的能力），具有多种应用领域-军事用途（“冲动”的传统用户）在搜索黄金之前（这种爱好在澳大利亚特别受欢迎）。
但是他也有一个很大的缺点-歧视方面存在很大困难，即 通过确定目标的类型，例如找出目标是有色金属还是黑色，还是将塑料盒中的杀伤人员地雷与一堆金属碎片区分开来？ 这个问题是什么原因造成的？
考虑脉冲金属探测器的工作原理。


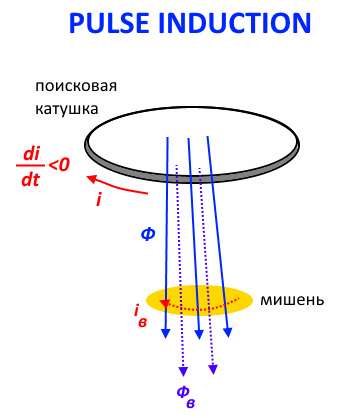
电子钥匙（通常是可以承受几百伏电压的MOSFET-例如，在马来西亚工程师的工作中使用了流行的IRF740 ，而在GreenPAK可编程模数矩阵的基础上使用了功能较弱的IRF730 ）来控制搜索线圈与电源（电池）的连接电池）。 当向晶体管的栅极施加控制脉冲（通常具有几百赫兹的频率）时， MOSFET断开-电路闭合，电流增加（逐渐由于过渡过程而逐渐）开始流经线圈。 我们正在等待数十或数百微秒的电流增加到所需的水平，然后...我们断开电路-控制脉冲已结束。 现时 $$$我$ 通过线圈，并因此产生磁通量 $$$\皮皮$ 线圈急剧减小（为加速MOSFET的闭合过程，控制脉冲不是直接提供给栅极，而是通过特殊的驱动器提供），由于电磁感应现象，导致出现EMF自感应现象 $$$e_L = -w {d \ Phi \ over dt}$ 线圈电压急剧上升。 然后，线圈上的电压电平开始下降。 但是，如果导电物体（“目标”）位于线圈附近，则磁通量与通过线圈的电流一起减小会感应出涡流 $$$i_in$ 在这个目标。 这些涡流产生自己的磁通量。 $$$\披肩$ ，它试图维持线圈的阻尼磁场。 这种影响导致线圈两端电压衰减的持续时间增加，这表明目标的存在与否（通过积分信号并估计积分值（ a ）或基于多个点（ b ）的信号值来做出决定:)


注意 ：脉冲也可以是双极性的（例如，在Vallon VMH2金属探测器中-用于扫雷的经典设备）：

（ 来源 ）
同时，由金属探测器产生的磁场的平均值（恒定分量）接近于零，这在目录中谨慎地指出（根据制造商的说法），这在寻找响应磁场的地雷时应防止破坏（尽管如书所述） 《用于人道主义排雷的金属探测器手册》 ，以及发生此类事件的人道主义排雷是不可能的）。

除了所描述的带有单个线圈的选件外，还结合了发射和接收功能，还有带有两个独立线圈的脉冲金属探测器。 该方案不仅用于金属搜索领域，而且还用于链接1 ， 链接2的缺陷检测（ 脉冲涡流（PEC）测试 ）中。 在这种情况下，一个线圈（ 发送/驱动线圈 ）用于激发目标中的涡流，另一个线圈 （ 接收/拾取线圈 ）是磁场传感器。 这种方法不仅可以在减小阶段（将电源与发射线圈断开连接之后）分析磁场，还可以在增大阶段（将电源连接到发射线圈之后）分析磁场：

这是对该技术的出色描述：

歧视问题
识别金属类型的问题来自以下事实：线圈上的最终电压曲线受靶材的大小和形状，靶材与线圈的距离以及电导率（比电导率）的影响 $$$\ sigma$ ）和磁导率 $$$\亩$ ）目标材料的特性。
以下是有关此主题的一些引文：

（来源： Ahmet S. Turk，Koksal A. Hocaoglu，Alexey A. Vertiy地下传感）

金属类型的区分-由于脉冲感应通过异常脉冲衰减所需的时间来检测金属，因此通常仅用于检测金属，而不是确定金属的类型。

（ 来源 ）

...大小，深度，周围目标和土壤响应可能会以无法正确识别的方式改变信号。

（ 来源 ）

已经做出了许多尝试来创建能够区分铁，银和铜的脉冲金属检测器，但是所有这些尝试都取得了非常有限的成功。 这是由于脉冲信号的物理性质。

（ 来源 ）

解决此问题的一种方法是使用Double-D （ DD ）线圈代替通常的单回路 ，例如，在流行的Minelab GPX系列金属探测器中：

（ 来源 ）
在这样的线圈中，发射线圈（ TX ）和接收线圈（ RX ）被划分为：

（ 来源 ）
在这种情况下，不仅在目标信号减小时，而且在发送线圈中电流上升时，都对目标信号进行分析。 但是这种区分不是很可靠：

（ 来源 ）
但是单环线圈呢？ 许多工作（ 链接1 链接2 链接3 ）表明，来自目标的线圈中的信号可以表示为衰减指数信号的加权和，其最大值和时间常数是独立的，并取决于目标的材料，大小和形状：
$$$u（t）= \ sum_ {i = 1} ^ NA_ie ^ {-t / \ tau_i}$
使用美国陆军标准金属探测器进行的辨别实验报告，在本文作者进行的实验中，单个物体就很好地表征了小物体。 $$$Ae ^ {-{\ alpha} t}$ ，对于大型物体，已经需要两个- $$$Ae ^ {-{\ alpha} t} + Be ^ {-{\ beta} t}$ 。
本文指出，指数成分的时间常数可以表示为等效电感与电阻之比 $$${\ tau} _e = {L_e \ over R}$ 它的表达式是针对具有底边半径的圆柱体 $$$R$ 又高 $$$h$ ：
$$$\ tau = {{\ mu_r \ mu_0 \ sigma R ^ 2 h} \ over 8}$
本文给出了半径为球形的涡流衰减时间常数的表达式。 $$$R$ ：
$$$\ tau = {{\ mu_r \ mu_0 \ sigma R ^ 2} \ over \ chi ^ 2}$ ，
在哪里 $$$\ chi$ 是求解方程式的结果 $$$tg \ chi = {{（\ mu_r-1）\ chi} \ over {\ mu_r-1 + {\ chi} ^ 2}}$

注意 ：此类解析表达式仅适用于简单对称物体。 因此，要研究涡流，可以使用软件包对电磁过程进行数值模拟。 一个示例是在COMSOL Multiphysics软件包中模拟涡流电磁制动器：

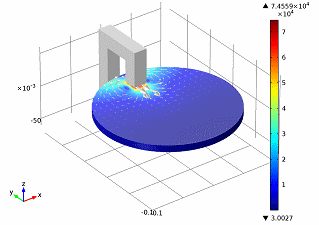
（ 来源 ）

可以看出，时间常数的表达式一起包括磁导率，电导率和目标尺寸。 区分这些因素所需要的这些因素的影响并不是那么简单。
在已经提到的工作中，建议使用贝叶斯分类器从金属碎片中区分出地雷（测试了两个假设： $$$H_0$ -垃圾 $$$H_1$ -我的），但这需要对信号的对称性进行其他估算，等等。 （有趣的是，所用因素的组成包括信号能量，估计为 $$$\ sum_ {i = 1} ^ N {u_i ^ 2 \ cdot {\ Delta} t}$ ）
为了说明这一点，我在实验台的屏幕上构建了针对各种目标的线圈两端电压图表的原始设计：
无目标：

距线圈不同距离的目标编号1（黑色金属）：

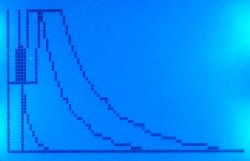目标数字2（黑色金属）：

距线圈不同距离的目标编号3（有色金属）：

目标数字4（有色金属）：

可以看出，由于较高的磁导率，黑色金属靶材比非黑色金属靶材具有更高的初始信号水平，但是由于电导率较低，信号衰减更快。
神经网络
然后，如何基于这些非常严格的特征对目标进行分类，特别是在更改目标与金属探测器线圈之间的距离时？ 我们有一个很棒的工具-人工神经网络。 神经网络玩井字游戏， 二十一点 ， 扑克 ，预测天气和葡萄酒质量 ，计算对农业机械运动的抵抗力 ...因此我们可以使用神经网络解决歧视问题！
伊朗研究人员发表的文章“通过使用神经网络提高PI系统的性能”证明了这一点：

神经网络的数据
为了填充数据阵列以进行神经网络的训练，验证和测试，当我按下测试台上的按钮时，会在电压曲线上测量8个点（根据经验选择的点数），并且ATmega328 ADC在连接到计算机USB连接器的串行端口中以符号形式读取。
在运算放大器输入前面的架子上，一个二极管限幅器被打开，但是，正如仿真所示，在我们感兴趣的区域（线圈上的电压很低），它对电压值的影响可以忽略不计：

在终端程序（例如Tera Term ）中打开日志记录模式，我们获得“原始”数据（为方便起见，可以在Tera Term中将注释添加到协议中）。 用Go编写的一个小工具将这些数据转换为适合神经网络使用的格式：
i1 i2 ... i8 o1 o2
具有一组值的行的示例：
588352312312280252240206192 0 1
输入数据i1 i2 ... i8是范围为0 ... 1023的10位ADC的样本。
输出o1 o2的形式为：
“有色金属”（ 1 0），“有色金属”（0 1 ）。
当线圈附近有一个黑色金属制成的目标（第1号目标，第2号目标）和有色金属目标（第3号目标，第4号目标），并且目标与搜索线圈​​的距离不同时，我收集了数据。 为了进一步使用，我们选择了与足够的信号电平相对应的数据-至少具有两个非零值。 与ADC输入过载相对应的数据集也被丢弃-包含几个最大可能值（1023）：

为了说明这一点，我对一个数据集进行了回归分析：

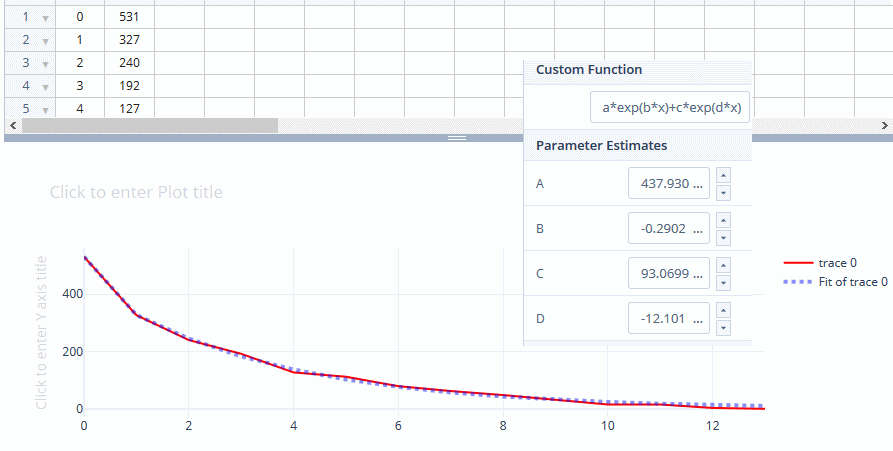
接收信号由两个指数之和很好地描述：
$$$437.9e ^ {-{0.29} x} + 93.1e ^ {-{12.1} x}$ 在哪里 $$$x$ -参考编号。
我分配了大部分数据（110套值， train.dat文件）用于训练（ 训练数据集 ）（它们还被随机分配了-在加载过程中随机排列），而较小的部分（40套， test.dat文件）进行了神经网络验证 （ 验证数据集 ）-以最简单的形式进行交叉检查（针对延迟数据（保持数据集 ））。
神经网络结构
创建的经典直接分布神经网络将分为三层：
输入层 -8个神经元-感知电压曲线的点；
隐藏层 -三个神经元；
输出层 -两个神经元。

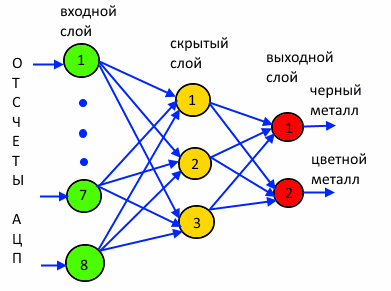
（网络“ 8-3-2”）
在上述工作中，伊朗人在两个隐藏层中使用了两个样本（分别是两个输入神经元）和三个神经元（在他们的文章中不太清楚地描绘和描述了神经网络图）。
神经元状态 $$$z$ 定义为加权（ $$$w$ -重量） $$$n$ 输入信号 $$$x$ （树突状感知）和偏见 $$$b$ ：
$$$z = \ sum_ {i = 1} ^ nw_i \ cdot x_i + w_ {i + 1} \ cdot b$
（偏倚的增加可以表示为附加神经元偏倚的影响）
使用激活函数将神经元的状态转换为输出信号（在轴突端子处） $$$f$ ：
$$$y = f（z）$
到达输入层神经元的神经网络的输入信号未更改地传输到其输出，这对应于线性激活函数：
$$$f（z）= z$
对于隐藏层和输出层的神经元，使用非线性激活函数“ Sigmoid”，或者更受欢迎的选择是逻辑函数Logistic函数，其值的间隔为（0; 1）：
$$$f（z）= {1 \超过{1 + e ^ {-z}}}$
对于非负ADC采样，激活功能的这种选择非常有用。 但是，当然，这需要对输入值进行规范化-将它们除以1024，以保证值小于1。
伊朗人使用双曲正切作为激活函数。
输出层神经元输出端的值决定了神经网络的结果。 具有最大输出值的神经元将指示网络做出的决定（获胜级别）：第一类是“黑色金属”，第二类是“有色金属”。
伊朗人使用了三个输出神经元，分别表示铁，铜和铅。
Python通常用于解决机器学习问题-PyTorch ， Keras ， TensorFlow ， CNTK ，神经网络的库和框架也为JavaScript - Synaptic ， Java - Deeplearning4j ， C ++ - CNTK和MATLAB 紧随其后。
但是对于随后在金属探测器中“现场”使用，这些框架/库几乎没有用，因此，为了详细了解过程，我在不使用其他ANN支持库的情况下构建了神经网络。 当然，神经网络也可以用BASIC :-)编写。 但是在主观偏好的影响下，我选择了Go 。
神经网络训练与验证
创建网络时，权重会使用（-0.1; 0.1）范围内的随机值进行初始化。
我使用随机梯度下降 （ SGD ）方法训练网络。
神经网络使用顺序训练提供的数据集之一执行学习过程的一次迭代。 在这种情况下，首先执行直接分配操作-网络处理从提供给输入的训练示例提供的信号集。 然后，基于所获得的解，实现反向传播算法。 为了更新学习过程中的量表，我应用了“香草”梯度下降公式，该公式使用一个超参数- 学习速率系数 $$$\ alpha$ （有时表示 $$$\ eta$ ），即 未使用第二个流行的超参数-矩因子 $$$\伽玛$ （ 动量因子 ）。
使用完整的训练数据数组后，学习时代结束了。 在时代结束之后，计算出训练的误差均方根 （ Mean Squared Error （ MSE ）），为神经网络提供了一组用于验证的值（对递延数据进行交叉检查），确定了验证误差的均方根，预测的准确性（ 准确性 ）和循环重复。 达到验证误差均方值的所需水平后，循环停止。
编译源代码（文件nn4md.go ）并启动可执行文件后，学习过程将显示在控制台时代（ Epoch ），学习和验证错误的平均平方（ MSE ）以及对验证数据集的预测准确性（ Acc 。）。
这是此类协议的一部分：

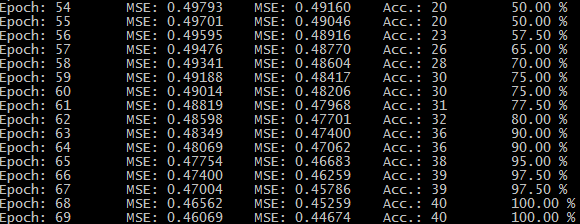
起始数字的变化会影响神经网络权重的初始值，从而导致学习过程中的微小差异。 学习速度因数为0.1时，大约需要300个纪元才能完成学习（当测试集上的MSE = 0.01时）。
验证数据集决策的准确性为100％（程序给出获胜神经元的数量，从0开始-“ 0”-第一个神经元，黑色金属；“ 1”-第二个神经元，有色金属）：

0-> 0
0-> 0
0-> 0
...
1-> 1
1-> 1
1-> 1

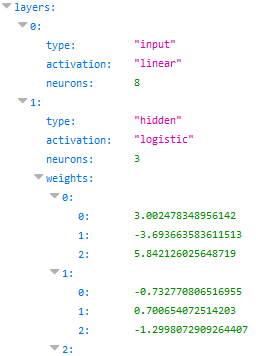
训练后得到的神经网络权重将存储为JSON格式的nn4md.json文本文件，以供以后使用。 顺便说一下，要在Go上编码JSON结构，请使用此在线工具很方便。
由于尚未开发出一种用于存储神经网络设置的格式的普遍接受且方便的标准（当然，尽管有NNEF-但是对于这样一个简单的网络，这太恕我直言了），我使用了自己的格式：

神经网络测试
现在，我们正在测试训练有素的神经网络，以识别新目标（ 测试数据集 ）。
目标数字5（来自黑色金属） ：
曲线类型：

一组值：
768 224 96 48 14 0 0 0
目标数字6（来自有色金属） ：
曲线类型：

一组值：
655 352 254 192 152 124 96 78
在完成培训之后，程序将期望输入数据进行测试。
检查目标编号5：

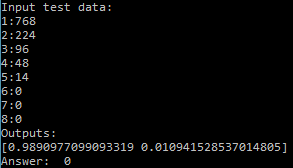
成功-“ 0”-黑色金属。
现在检查目标编号6：

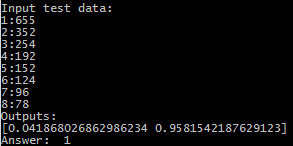
成功-“ 1”-有色金属。
那几乎被证明是“ 概念证明 ”。
数据集文件，网络权重文件和源代码在GitHub上的存储库中可用。