总结
给出了在n皇后分布问题的所有解决方案的顺序列表中建立的定律的描述。 确定:
- 完整解决方案在所有解决方案总列表中的比例随着n值的增加而降低。
- 完整解决方案以所有解决方案的顺序列表分布,以这种方式,很可能会找到列表中彼此靠近的完整解决方案。
- 所有解决方案的总列表中完整解决方案的顺序是对称的。 如果在列表开头的第i个位置解是完整的,则位于位置n-i +1处的列表末尾的对称解也将完成(解的对称性规则)。
- 在所有解决方案列表中对称放置的所有简短解决方案和完整解决方案对都是互补的-相应行的位置索引之和是恒定的,并且等于n +1(解决方案的互补性规则)。 这表明,所有完整解决方案列表中只有前半部分是“唯一的”,列表中后半部分的任何完整解决方案都可以基于互补规则来获得。 该规则的结果是,对于任何n值,完整解的数量将始终为偶数。
- 解决方案矩阵的行的单元格的活动相对于通过此矩阵中间的水平轴对称。 这意味着第i行的单元格的活动始终与第n-i + 1行的单元格的活动一致。 活性是指细胞指数在完整溶液列表的相应行中出现的频率。 同样,解决方案矩阵的各列单元格的活动关于垂直轴对称,将矩阵分为两个相等的部分
- 与n无关,在对所有解的顺序搜索中,第一个完整解仅在一定顺序的短解之后出现。 简短解的初始序列的大小随n增加。 对于n的偶数,在出现第一个完整解之前的简短解的列表长度明显长于最接近的奇数。
- 决策矩阵中的难点开始向前发展并形成第一个短期决策的那条线根据黄金分割率规则对矩阵进行划分。 对于较小的n值,这样的结论是近似的,但是,随着n值的增加,这种结论的准确性会渐近地增加到标准规则的水平。
该出版物呈现了文章[1]的主要结果,该文章发表在“人工智能建模,2018,5(1)”期刊上。 在哈布雷(Habré),有一些与n-皇后问题有关的作品: [2] , [3] ,
在nxn大小的棋盘上分配n个皇后的问题历史悠久。 它最初是由M. Bezzel [4]于1848年制定的,是常规棋盘的一项智力任务。 随着时间的流逝,F。Nauck [5]扩大了对问题的陈述,而棋盘的大小可以具有任何价值。
引言
问题的说明非常简单:您需要在大小为nxn的棋盘上分配n个皇后,以便在每一行,每一列以及穿过女王所在位置的单元格的左右对角线上,最多只能有一个皇后。 此任务易于理解或向某人解释,但解决起来却相当困难。 事实是,没有规则可以为每行安排皇后以获取解决方案。 解决方案只能通过列举某些行中皇后排列的各种变体来获得。 但是,这种解决方法的复杂性在于,皇后排列的所有变体的数量都随着n的增加而呈指数增加。 此外,向前迈出一步以将女王/王后放置在某一行的自由位置上会导致其余行的自由位置列表发生变化,并且在返回一步时为了形成搜索分支,有必要清除先前执行的动作的痕迹。
有大量的出版物涉及解决n皇后问题的各个方面。 它们可以归因于几个研究领域:针对给定棋盘大小(n)的值搜索所有完整的解决方案,开发一种针对n的不同值找到一个解决方案的快速算法,将完整问题的解决方案转换为完整解决方案,以任意组合k个皇后,问题算法计算的计算复杂性,以及对问题的原始公式的各种修改。 为了熟悉这些领域,我将推荐B. Jordan,S. Brett [6]和IP Gent,C. Jefferson,P. Nightingale [7]的有趣出版物,它们提供了各个研究领域的相当详细的概述。 特别值得注意的是沃尔特·科斯特斯(Walter Costers )支持的互联网出版物[8] ,该出版物是由莱顿大学的一个小组编写的,其中包含指向342个与n-皇后问题有关的出版物的链接(截至2018年12月)。
尽管n皇后问题一直活跃了150多年,并且在此期间出现了大量出版物,但我找不到在解决该问题的结果中与寻找模式相关的工作。 与寻找所有解决方案有关的大多数项目很可能没有保存找到的解决方案,也没有看到“内部”内容,在问题陈述中还有其他主要目标,而我们尊敬的同事实现了这些目标。 但是,在遥远的地方,在我看来,情况类似于一个人煮鸡蛋作早餐,但不吃鸡蛋,而是扔掉它们,只留下了一些煮鸡蛋的记忆。 我一直确信,如果数据不是随机的,那么即使我们找不到这种规律性,它们也应该有一定的规律性。 正是这种信念是在此任务中寻找模式的原因。
除了希望为Habr社区的成员提供有用的信息以供思考之外,我希望有才华的程序员(其中大多数是Habr成员)更加关注计算机仿真(计算仿真)这样的发展方向。 作为一种研究方法,“算法数学”被用于许多领域的“前沿”:人工智能,软件科学,数据科学……我相信在算法数学的基础上将解决非常复杂和重要的实际应用问题否则。
定义
在下文中,我们将用符号n表示棋盘的大小。 如果将所有n个皇后号始终放在棋盘上,则该解决方案将称为“完整”。 所有其他解决方案,当正确放置的皇后数量少于n时,我们称其为短解决方案。 通过解的长度,我们指的是正确放置的皇后数(k)。 对于给定值n,所有解决方案的数量将由m表示。 作为大小为nx n的“棋盘”的类似物,我们将考虑大小为nx n的“解决方案矩阵”。
开始
为了进行研究,开发了一种算法来搜索n任意值的所有解。 我们没有使用标准递归或通常的嵌套循环系统。 对于较大的n值,这种方法将存在很大问题。 该算法是基于一组交互事件建立的,在每个交互事件中都发生了某种相互关联的动作系统。 这样就可以简单地实现一种机制,该机制可以在选择问题解决方案的分支中的下一个节点时进行状态空间更改(正向跟踪),或者在返回一个或多个步骤时可以清除先前执行的操作的痕迹(向后跟踪)。 算法中对内存大小或处理器速度没有特殊要求。
基于此算法,找到了解决方案矩阵n =(7,...,16)的各种值的所有顺序解决方案(简短和完整)。 由于完整解决方案列表的大小是命名序列“整数序列在线百科全书” (序列A000170 [9]),并且在许多出版物中都有提及,因此对于我们考虑的n个值,列出所有解决方案列表的大小(短+完整)对我来说似乎很有趣: 7 (194), 8 (736), 9 (2936), 10 (12774), 11 (61076), 12 (314730), 13 (1716652), 14 (10030692), 15 ( 62 518 772), 16 (415 515 376)。
此外,使用找到的解决方案,我们给出了一些问题的措辞,解决这些问题的方法以及对结果的描述。
1.搜索解决方案的状态空间
枚举尺寸决定为n的矩阵的某些行中的皇后排列的各种选择导致状态空间的形成。 如果不禁止在矩阵的一个或另一个单元中布置皇后,则状态空间的大小将为n n 。 如果仅考虑禁止在每一行和每一列中放置多个皇后的规则,那么我们将获得状态空间的子集,其大小将等于n! 状态空间的这个子集对应于车队分配n的问题。 如果与此同时,如果我们还考虑到禁止在女王对角线穿过的单元格左右对角线上放置一个女王/王后的规则,那么我们将得到一些搜索空间,其大小将小于n!..我们称这样的状态空间子集-一个高效的搜索空间,基于以下事实:只有在此子空间中才是所有可能的解决方案。 生产性搜索空间中任何已完成的分支都是正确放置了一定数量皇后号的解决方案。 基本上,这些是短期决策,只有一小部分是完整决策。
图1显示了三个指标的自然对数图:a)阶乘值(n!)关于决策矩阵的大小; b)所有决定的数量(简短和完整的决定); c)完整溶液的数量,取决于溶液矩阵(n)的大小。 如预期的那样,所有曲线的特征都是随着n的增加呈指数增加。 尽管由于n值的样本量较小,所有解决方案的数量和完整解决方案的数量的增长率都不同,但是在图中不太明显。 例如,对于n = 13,这些指标的对数之间的差异为3.148,对于n = 16,此差异增加0.190且为3.338。 显然,随着n的进一步增加,这种差异将更加明显。

图1状态空间大小的对数与值n的依赖关系
2.完整决策在所有决策的总清单中所占的比例如何变化?
显然,如果完整解数的增长率落后于所有解数的增长率,那么随着n值的增加,在所有解的总列表中找到完整解的可能性将降低。 图2显示了所有解的总列表中完整解的比例在n值上的图表。 可以看出,随着解决方案矩阵大小的增加,一般列表中所有完整解决方案的份额都会减少。 对于初始值n =(7,...,14),该值从值0.2062减少到5.364倍至0.0364,然后此值逐渐逐渐减小。 在这里,两个陈述之间出现了形式上的矛盾:一方面,完整解决方案的数量随着n的增加而呈指数增长,另一方面,在所有解决方案的顺序列表中,完整解决方案的概率不断降低。 这种看似悖论的解释很简单,生产空间的大小以及所有解决方案列表的相关大小随着n的增加而比完整解决方案的数量增长得更快。 这就像试图在大海捞针中寻找针叶一样-“随着n的增加”,干草量的增长快于那里丢失的针叶数量。 因此,我们可以假设,如果n = 27,则完整解的数量约为2.346 * 10 17 ,那么所有解的数量的对应值很可能比〜10 20大3-4个数量级。
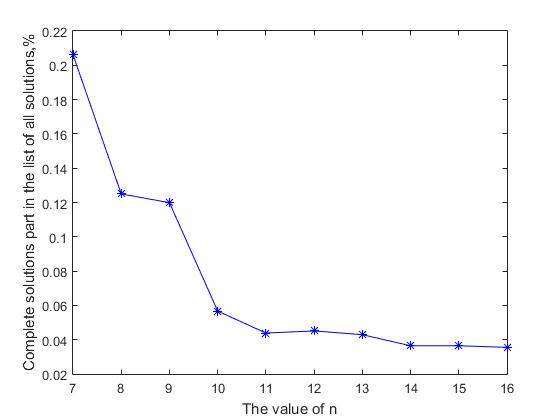
图2随着n的增加,所有解决方案总列表中完整解决方案的比例减少
3.在所有解决方案列表中,各种长度的解决方案的频率是多少?
如前所述,生产性搜索空间中所有已完成的分支都是正确放置了不同数量皇后的解决方案。
我们感兴趣的是,所有解决方案的总列表中以何种频率存在各种长度的解决方案。
表1中的值n =(7,...,12)给出了具有不同长度的解的相对频率的相应值。 此数据的相应视觉表示如图3所示。
通过分析表,我们可以得出以下结论:
a)对于大小为n的每个矩阵,解的一定长度具有最大频率(以粗体突出显示)。
表1.对于大小为n =(7,...,12)的矩阵,不同长度(k)的溶液的相对频率(%)
| \ | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
|---|
| 7 | 10.31 | 31.23 | 27.84 | 20.62 | | | | | |
| 8 | 2.45 | 20.38 | 34.78 | 29.89 | 12.50 | | | | |
| 9 | 0.34 | 5.79 | 21.73 | 35.83 | 34.32 | 11.99 | | | |
| 10 | 0.05 | 1.35 | 8.41 | 25.62 | 32.94 | 25.96 | 5.67 | | |
| 11 | | 0.15 | 2.12 | 11.80 | 26.71 | 34.47 | 20.36 | 4.39 | |
| 12 | | 0.01 | 0.29 | 3.28 | 13.56 | 29.88 | 31.29 | 17.18 | 4.51 |
b)随着n的增加,具有不同长度的解决方案的数量也会增加。 因此,所有决策的相对频率都会降低。
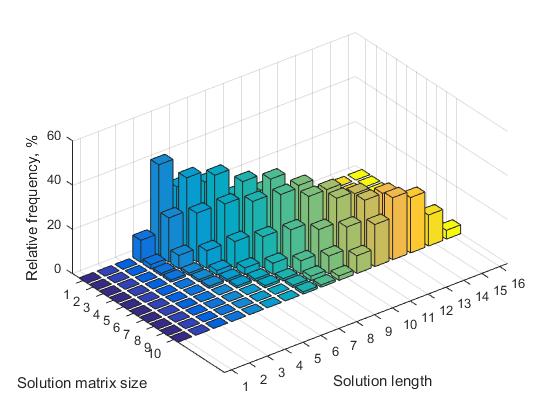
图3取决于解矩阵大小的各种长度的解的频率n = 7,...,16
c)对于大小为n的每个矩阵,都有一定长度的最小解长度,在该最小长度以下不会发生短解。 随着n的增加,此阈值的值也增加。 例如,对于n = 8,阈值分别是4,对于n = 16,阈值是7。
4.完整解决方案在所有解决方案的顺序列表中的相对排列方式是什么?
在关于“ n个皇后的分布”的问题的陈述中,没有理由会给出理由对所有解决方案的一般列表中的完全决策的顺序做出任何假设。 我们对一般列表中的完整解决方案是否均匀,随机分布或是否具有某些特殊性感兴趣。 为了找出答案,我们在所有解决方案的顺序列表中分析了最接近的完整解决方案之间的距离。 从图4可以看出,在n = 12的情况下,给出了相应频率的变化图,
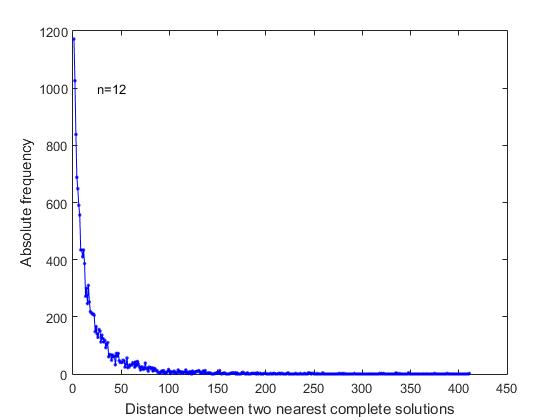
图4频率对所有完整解的顺序列表中最接近的完整解之间的距离(n = 12)
在所有解决方案的公共顺序列表中,有最完整的解决方案以最快的速度彼此紧追。 这是搜索分支形成的情况,当最后几行中的自由位置之间的关系允许您形成两个或多个连续的完整解决方案时。 此外,最大频率是位于其间的那些完整解:一个简短的解决方案,两个简短的解决方案,等等。
5.在所有解决方案的总清单中,完整解决方案的排列方式是否有规律?
为了回答这个问题,我们分析了值n =(7,...,16)的所有解决方案的顺序列表。 为了清楚地说明结果,在图5中,对于值n = 8,显示了一个图表,其中依次指示了所有736个溶液列表中每个溶液的长度。 在这里,只有92个解决方案是完整的,并且以红色突出显示,其余644个解决方案是简短的并且以蓝色突出显示。 可以看出,完整的解决方案并没有在所有解决方案列表中平均分配。 在某些情况下,完整的解决方案更为普遍,而在某些地方则很少或根本没有完整的解决方案。

图5对于8 x 8矩阵(红色-完整溶液,蓝色-短溶液),按顺序列出所有溶液的长度。 所有解决方案的总数是736
但是,这里还有其他重要的事情。 如果您仔细查看类似蓝红色条形码的图形,您会注意到一个非常重要的功能,所有红线相对于通过解决方案列表中间的某些条件垂直线是对称的。 实际上,如检查所示,如果在常规列表的第i步有一个完整的解决方案,那么肯定会在步骤m-i + 1找到一个完整的解决方案。 例如,对于n = 8,如果在步骤43中出现了对所有解的顺序搜索中的第一个完整解,那么相应地,在步骤736–43 + 1 = 694中可以找到列表中的最后一个完整解。 如果在步骤368中出现了10x10矩阵的第17个解,则在步骤12774-17 +1 = 12407中,与其对称的完整解出现在所有解的列表中。 该规则适用于任何大小的决策矩阵。 因此,我们可以制定一条规则。 对于任何n值,如果在所有解的顺序列表中,从列表开头的第i个位置解是完整的,则位于m-i +1位置的列表末尾的对称解也将是完整的(解的对称性规则)。 m, , . , n, , . ( – ).
, – . n+1 . , 17- n=10 368- (1, 5, 7, 10, 4, 2, 9, 3, 6, 8).
, 12407 (10, 6, 4, 1, 7, 9, 2, 8, 5, 3). , (11, 11, …,11). n, , , . . n, ( , ), , – n+1 ( ). Q(i ) Q1(i) – ,
<b>`Q ( i ) + Q1 ( i ) = n + 1, i = (1, n) `</b>
该规则意味着,如果在第i步获得了一个完整解,则在步骤m-i +1处的对称完全解是已知的。 因此,在搜索所有完整解决方案时,仅查找所有完整解决方案的前半部分就足够了。 完全解决方案列表的后半部分可以根据互补性规则,从已经获得的解决方案中确定。 达到完整解决方案列表的一半的标准是满足先前完全解决方案Q(i-1)和后续Q(i)之间的互补规则。 即,两个连续解的每对对应索引的和必须等于n +1 。 由于所有完整解决方案列表中的任何完整解决方案都是唯一的,因此只有那些连续的完整解决方案才是互补的,它们在将列表分成两半的边界的两侧。
将来,这两个规则将允许在搜索所有下一n值的完整解时,将计算量减少,从而将计算时间减少一半。
6.可视化找到第一个完整解决方案的步骤顺序
在形成解决方案搜索的一个分支时,执行前进(前进跟踪)和返回(前进跟踪)步骤的过程如何? 为了回答这个问题,对于10 x 10的矩阵,我们确定线之间的初始194过渡的顺序,直到出现第一个完整解。 相应的图如图6所示。蓝线表示前进,红线表示返回。 在这194个步骤中,创建了35个简短的解决方案。 该图显示大多数过渡(84.5%)发生在线(5、6、7、8)之间。 这是通往“目标”途中的“瓶颈”。 从图中可以看出,只有7种情况切换到第4行,一种情况切换到第3行。 还有13种切换到第9行的情况。 试图移动到第10行的三次尝试均未成功,因为在第10行的这些搜索分支中没有空位。 这个例子展示了短的所有分支

图6前194个搜索步骤(n = 10)的回溯(红色)和正向跟踪(蓝色)事件的可视化
解决方案,直到第一个完整的解决方案。 如果任何解决此类问题的算法都包含消除所有(或部分)导致短期解决方案的分支的机制,则该算法将是有效的。
7.第一个完整的解决方案出现了几项简短的决定之后?
考虑到完整解决方案在所有解决方案列表的不同部分上的显示方式有所不同,因此当按顺序搜索所有解决方案时,找出第一个完整解决方案出现了多少个简短解决方案似乎很重要。 为此,对于值n =(7,...,35),依次计算所有短解,直到出现第一个完整解。 从图7可以看出,该图显示了对n的依赖关系图,即步数的自然对数,当出现第一个完整解时,对于n的偶数,第一个完整解的出现要比n的最接近奇数晚得多。 例如,对于奇数值n = 21,第一个完整解出现在步骤3138,而对于下一个偶数值n = 22,第一个完整解出现在步骤628169。 因此,对于下一个奇数值n = 23,在步骤9155中出现第一个完整解。

图7对于n的各个值,直到第一个完整解为止的简短解的数量
偶数n = 22时的迭代步数分别比最接近的奇数多200.2和68.6倍。 这在n = 34的计数时间中尤其明显。 在这里,第一个完整解出现在第826 337 184步,对于最接近的奇数(33,35),分别出现在第50 704 900和84 888 759步。 还应该说,在出现第一个完整解之前,随着n的增加,短解的数量单调增长。 对于n的偶数,这在n = 19时发生,对于奇数,在n = 24和n = 26时发生。
8.所有完整解决方案列表中每一行的像元频率是否相同?
nxn大小的决策矩阵,类似于棋盘,就像发生所有事件的场景一样。 在此场景上形成的任何完整解决方案都包含不同行的单元格的索引,因为 每个此类单元格都是解决方案搜索分支中的一个节点。 我们感兴趣的问题如下:形成所有完整解决方案的列表时,不同单元格中每一行的负载是否相同? 显然,频率值越高,此单元格在形成完整解列表时的活动性就越高。 为此,我们根据所有完整解决方案的列表为每一行确定各种索引的相对频率。 首先,我们分析大小为n = 8的解决方案矩阵。 让我们依次检查完整解数组的每一行,并确定各种索引值的频率。 表2示出了八行中的每行中不同小区的绝对活动频率的对应值,并且在图3中。 8
表2.基于对所有完整解决方案列表的分析,细胞活动在8x8决策矩阵的八行中的每行中的绝对频率
| 行\ col | 1个 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
|---|
| 1个 | 4 | 8 | 16 | 18岁 | 18岁 | 16 | 8 | 4 |
| 2 | 8 | 16 | 14 | 8 | 8 | 14 | 16 | 8 |
| 3 | 16 | 14 | 4 | 12 | 12 | 4 | 14 | 16 |
| 4 | 18岁 | 8 | 12 | 8 | 8 | 12 | 8 | 18岁 |
| 5 | 18岁 | 8 | 12 | 8 | 8 | 12 | 8 | 18岁 |
| 6 | 16 | 14 | 4 | 12 | 12 | 4 | 14 | 16 |
| 7 | 8 | 16 | 14 | 8 | 8 | 14 | 16 | 8 |
| 8 | 4 | 8 | 16 | 18岁 | 18岁 | 16 | 8 | 4 |
呈现了一组4个图形,其中每个图形都描述了一条线内相对频率的变化。 可以从对所有获得的数据进行分析得出的根本重要结论之一如下:
- 对于任意大小n的决策矩阵,第i行的单元格的活动与单元格n-i + 1的活动一致,即 第一行的单元格的活动始终与最后一行的单元格的活动一致,第二行的单元格的活动与倒数第二行的单元格的活动一致,等等。
如果n为奇数,则仅解矩阵的中间行不具有对称对;对于所有其他单元格,以上规则有效 - 我们称其为“溶液矩阵不同行的单元的活动的水平对称性” 。 因此,由于行(1、8),(2.7),(3.6)和(4.5)的单元格活动的对应图完全相同,因此对于大小为n = 8的决策矩阵,我们仅提供了4张图。
还应注意,频率值关于将矩阵分为两个相等部分(在n为偶数的情况下)或通过中值列(在n为奇数的情况下)的垂直轴对称。 我们称其为“溶液矩阵不同行的细胞的活性的垂直对称性” 。
另外,根据表2的分析,如下所示,解矩阵中的频率关于左右主对角线对称。
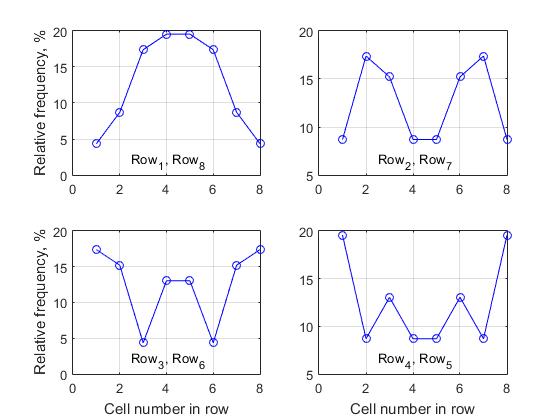
图8形成完整解的列表时相应行的单元格活动,n = 8
我认为问题陈述中存在限制性规则,以及不确定性的相关属性,“形成”了不同线路节点之间的一种和谐关系。 符合这些规则的搜索分支会导致形成完整的解决方案。 搜索的其余分支在某些步骤上违反了这些规则,因此,以短期决策的形式“完成了他们的旅程”。 在此应注意,决策矩阵的单元在投影影响组内仅具有局部关系,在它们之间没有针对协调动作的规定规则。 细胞的集体活动只是限制性规则影响的结果。 因此,一个相当有趣的问题仍然悬而未决:限制性规则(如非确定性因素)如何影响决策矩阵的单元,最终导致形成“和谐”的单元活动矩阵-相对于水平轴和垂直轴以及相对于左侧对称和右主对角线。 这是仅此问题的特征属性,还是对其他非确定性问题也适用?
9.从哪个行号打开正向跟踪-向后跟踪算法?
如果在皇后区位置的决策矩阵中遵循顺序行选择算法的操作,我们可以看到,从某行开始(我们将其称为“ StopRow”),前进的过程被“打破了”。 在搜索分支中,这是第一行,其中存在免费提供问题

图 9-1 StopRow索引与n的比率与决策矩阵大小的关系(第1部分)
女王位置的位置。 正是从这一行开始,向后跟踪算法被打开,以清除先前执行的动作的痕迹并返回。 这是第一个简短解决方案出现的行。
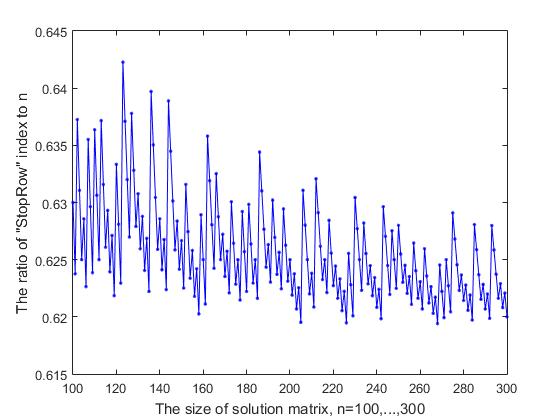
图9-2 StopRow索引与n的比率与决策矩阵大小的关系(第二部分)
困难开始开始的“ StopRow”行的索引取决于决策矩阵的大小n。 如果我们考虑该索引的比率(用StopInd表示)与解决方案矩阵n的大小,则从图9-1可以看出,其中给出了初始值n =(7,...,99)的计算结果,该比率上下波动或大或小并倾向于减少。 随着n =(100,...,300)的增加,该比率在0.619-0.642之间波动(图9-2),随着n的进一步增加,我们得到以下结果(n的值依次给出,括号中的值为StopInd和StopInd / n比率: 1000 (619,0.6190), 2000 (1239,0.6195), 3000 (1856,0.6187), 4000 (2473,0.6182), 5000 (3091,0.6182)。 -line根据黄金比例规则对决策矩阵进行划分 :即StopInd / n与(n-StopInd)/ StopInd的差异很小,随着n的增加趋于零。例如,对于n = 5000,关系之间的差异 3091/5000和1909/3091为0.006,小于这两个关系的平均值的0.1%。
两个图中显示的图形 9-(1,2)具有非随机形式的可变性,类似于“乐谱”上的录音。 可以看到以不规则的周期性反复跳跃和逐步下降。 显然,这种弯曲行为是有一定原因的,也许这将引起研究的兴趣。 因此,出于更详细的可视化目的,在两个图中显示了该图。
我只考虑了部分问题,这些问题可以根据“关于n个皇后的分布”问题的解决结果来提出。 我希望所获得的结果将使非确定性过程的形成和状态空间变化的机制对理解更加透明。 也许这将成为制定新任务和向前发展的支点。
结论
- 如果看一下出版物,我们得出了结论,那么自然就会出现问题:“文章标题中的十亿皇后问题解决方案是什么意思?” 在为哈伯准备出版物时,我认为一个人,例如,一个拥有开采钻石的地雷的人,应该至少给他的亲朋好友一颗钻石,否则将是不公平的。 因此,我想向habr社区的所有成员:参与者,组织者,访客致以礼物。 顾名思义,这是在十亿规模的棋盘上分配十亿个皇后的问题的解决方案。
当然,这不是多面钻石,但对于真正的知识艺术鉴赏家来说,它比“那里的某种钻石”更有价值。 而且,钻石在世界各地有许多不同之处,到目前为止,这种解决方案仅是一份副本。 我们的字节神(*)看到我在真诚地做这件事。
生成的解决方案是一个十亿个数字的一维数组,以MatLab .mat格式表示,并且可以在以下位置找到: Google Drive上的十亿个皇后区问题解决方案
-此数组的第一个元素表示女王/王后在第一行中的位置,第二个元素-第二行中的位置,等等。 这只是nBillion种可能解决方案中的一种。 nBillion的值是如此之大,以至于可以认为它是无穷大的近亲。
- 在我看来,这种解决方案可以归因于虚拟知识价值的范畴。 我们可以说“这是其中包含某些东西”。 它们确实不能被“触摸”,因此只有在感觉层面才能在意识中感知到它们。 实际上,那里有一个惊人的秩序,外在和内在的和谐。 这是纯粹的象征性礼物(从字面上和形象上讲),是送给社区所有成员的。 我认为,“ 您与众不同” 。
(我希望有人“把礼物带回家。”该文件足够大-3.7 Gb。这是经过验证的干净数据。Google云端硬盘会显示警告-请谅解。)
- 在做出这个决定之前,我考虑过这种礼物的个人集体性质。 是否有可能会提供一份原件,其余的会提供复印件? 但是解决方案很简单。 在这种情况下,通常的“原始”和“复制”的“日常”概念失去了意义。 我们不复制,而是创建另一个原件。 所有的“原始人”都是相同的,并且是同等的。
- 我认为,在亲戚的陪伴下,您很可能是唯一收到这种“智力产品”作为礼物的人。 如果您将这样的礼物告诉岳母,那会很有趣:“想象一下,母亲的棋盘长50,000 km x 50,000 km,上面分布着10亿个皇后,一个人在近距离看不到另一个……”。 谁知道,也许在此之后,女son会受到更多的赞赏,因为给了他如此奇怪的礼物。
我祝愿哈勃社区的所有成员健康,成功和幸福。 愿新的一年给我们大家带来好运。
(*)-由于它涉及对象的名称,因此也应给出其描述。
字节神是一个多维实体,由零和一组成,在每种意义上都是合理的,在各个方向上都是无限的。 这个空间中任何零和一的序列都代表一定的知识。
参考文献
[4] Max Bezzel,“ 8皇后问题的提案”,柏林日报,第1卷
3(1848),第363页。(以作者名称\ Schachfreund“提交。”)
[5] Franz Nauck,Briefwechseln mit allen fur alle“,《时代报》,第1卷
377第15号(1850),第182页。
[6]贝尔·乔丹; 史蒂文斯·布雷特(Stevens Brett)(2009)。 “对n皇后的已知结果和研究领域的调查。” 离散数学。 309(1):1-31
[7]根特,伊恩·P。 克里斯托弗·杰斐逊; 彼得·夜莺(2017年8月)。 “ n-Queens完成的复杂性”。 人工智能研究杂志。 AAAI新闻。 59:815–848
[8] W. Kosters及其所有,n-Queens-342个引用,(2018年11月20日)
[9] NJA Sloane,整数序列在线百科全书,以电子方式出版。 2016年