🤷 😰 👨🏼‍🎤 混沌的数学模型 🧕 🤳🏼 🎅🏻

引言

Habr已经在文章[1,2,3]中讨论了混沌理论。这些文章中考虑了混沌理论的以下方面：Chua发生器的广义图；建模洛伦兹系统的动力学；逻辑集成电路对Lorentz，Rössler，Rikitake和Nose-Hoover吸引子进行了编程。

但是，混沌理论技术也被用于对生物系统进行建模，而生物系统无疑是可以想象的最混乱的系统之一。动态均衡系统用于建模从人口，流行病的增长到心律不齐的所有事物[4]。

实际上，几乎所有的混沌系统都可以建模-证券市场生成的曲线可以使用奇怪的吸引子轻松地分析，用裸耳分析从泄漏的水龙头滴下的水滴的过程是随机的，但是如果描绘成一个奇怪的吸引子，它就会打开传统手段无法期望的超自然秩序。

本文的目的是通过使用以Python编写的简单直观程序为基础的数学模型的图形化可视化方法，通过增加生物种群数量和加倍机械系统中的周期的示例来研究混沌理论。

这篇文章是为教学目的而写的，但是即使没有编程经验的读者也可以使用上述程序独立地解决关于建模混沌现象的大多数新的教育问题。

以生物种群数量增长为例，将周期和混乱时期加倍

让我们从逻辑对数方程开始，该方程对生物学种群数量的有限增长而不是指数增长进行建模：

， （ ， ） 。 （ ） 美

$\ frac {dN} {dt} = aN-bN ^ {2}，（a，b> 0）。（1）美$

该方程式可以预测某些人群行为的外来和意外模式。确实，根据（1），对于

$t \ rightarrow + \ infty$ 人口规模接近等于a / b的边界。

对于逻辑微分解的数值解，可以使用最简单的算法，将时间步长的数值取为

$t_ {n + 1} = t_ {n} + h$ ，则解决方案（1）可以通过重复应用以下关系式获得：

（ ） 。

$N_ {n + 1} = N_ {n} +（aN_n-bN {_ {n}} ^ {2}）h。$ （2）

我们以有限差分的对数方程形式表示方程（2）：

$N_ {n + 1} = rN_ {n} -sN {_ {n}} ^ {2}$ 。（3）

其中： r = 1 + ah和s = bh 。
代入（3）

$N_ {n} = \ frac {r} {s} x_ {n}$ 我们得到了迭代公式：

（ ）

$x_ {n + 1} = rx_ {n}（1-x_ {n}）$ ，（4）

计算由关系式（3）给出的值，我们可以生成一个序列

， ， ，

$x_ {1}，x_ {2}，x_ {3}，.....$
在给定时间环境将支持的人口数量的最大值

， ，

$t_ {1}，t_ {2}，t_ {3}$ 。

我们假设存在表示种群总数一部分的分数的极限值：

$x _ {\ infty} = \ lim_ {n \ to \ infty} x_ {n}$ ，（5）。

我们将调查它的依赖性

$x _ {\ infty}$ 由等式（4）中的增长参数r得出。为此，在Python中，我们编写了一个程序，从

$x_ {1} = $ 0.$ 在r = 1.5; 2.0; 2.5的情况下，通过数百次迭代（ n = 200 ）计算结果：

程式码

# -*- coding: utf8 -*- from numpy import * print(" nr=1,5 r=2,0 r=2,5 ") M=zeros([201,3]) a=[1.5,2.0,2.5] for j in arange(0,3,1): M[0,j]=0.5 for j in arange(0,3,1): for i in arange(1,201,1): M[i,j]=a[j]*M[i-1,j]*(1-M[i-1,j]) for i in arange(0,201,1): if 0<=i<=2: print(" {0: 7.0f} {1: 7.4f} {2: 7.4f} {3: 7.4f} " . format(i,M[i,0],M[i,1],M[i,2])) elif 2<i<=5: print(".") elif 197<=i<=200: print(" {0: 7.0f} {1: 7.4f} {2: 7.4f} {3: 7.4f} " . format(i,M[i,0],M[i,1],M[i,2]))

程序的结果（为减少结果的输出，给出了前三个值和最后四个值）：

  nr=1,5 r=2,0 r=2,5 0 0.5000 0.5000 0.5000 1 0.3750 0.5000 0.6250 2 0.3516 0.5000 0.5859 . . . 197 0.3333 0.5000 0.6000 198 0.3333 0.5000 0.6000 199 0.3333 0.5000 0.6000 200 0.3333 0.5000 0.6000

对离散模型的分析表明，对于r = 1.5; 2.0; 2.5，随着迭代次数的增加，该值

$x_ {n}$ 稳定并几乎等于极限

$x _ {\ infty}$ ，由关系式（5）确定。此外，对于给定的r值，数量

$x _ {\ infty}$ 相应地相等

$x _ {\ infty} = 0.3333; 0.5000; $ 0.600$ 。
我们增加r = 3.1; 3.25; 3.5，迭代次数n = 1008，为此，我们对该程序进行了以下更改：

程式码

 # -*- coding: utf8 -*- from numpy import * print(" nr=3,1 r=3,25 r=3,5 ") M=zeros([1008,3]) a= [3.1,3.25,3.5] for j in arange(0,3,1): M[0,j]=0.5 for j in arange(0,3,1): for i in arange(1,1008,1): M[i,j]=a[j]*M[i-1,j]*(1-M[i-1,j]) for i in arange(0,1008,1): if 0<=i<=3: print(" {0: 7.0f} {1: 7.4f} {2: 7.4f} {3: 7.4f} " . format(i,M[i,0],M[i,1],M[i,2])) elif 4<i<=7: print(".") elif 1000<=i<=1007: print(" {0: 7.0f} {1: 7.4f} {2: 7.4f} {3: 7.4f} " . format(i,M[i,0],M[i,1],M[i,2]))

程序的结果（为减少结果的输出，给出了前四个和最后八个值）：

  nr=3,1 r=3,25 r=3,5 0 0.5000 0.5000 0.5000 1 0.7750 0.8125 0.8750 2 0.5406 0.4951 0.3828 3 0.7699 0.8124 0.8269 . . . 1000 0.5580 0.4953 0.5009 1001 0.7646 0.8124 0.8750 1002 0.5580 0.4953 0.3828 1003 0.7646 0.8124 0.8269 1004 0.5580 0.4953 0.5009 1005 0.7646 0.8124 0.8750 1006 0.5580 0.4953 0.3828 1007 0.7646 0.8124 0.8269

从上述数据可以看出，随着时间的变化，人口的分数部分在两个分数之间波动，而不是在一个有限的总体附近保持稳定。与r = 3.1相比， r = 3.25的循环周期是原来的两倍，而r = 3.5的循环周期是原来的四倍。

图形显示人口增长周期的程序

 # -*- coding: utf8 -*- import matplotlib.pyplot as plt from numpy import * M=zeros([1008,3]) a= [3.1,3.25,3.5] for j in arange(0,3,1): M[0,j]=0.5 for j in arange(0,3,1): for i in arange(1,1008,1): M[i,j]=a[j]*M[i-1,j]*(1-M[i-1,j]) x=arange(987,999,1) y=M[987:999,0] y1=M[987:999,1] y2=M[987:999,2] plt.title('     r=3,1;3,25;3,5') plt.plot(x,y, label="T=1,ymax=%s,ymin=%s"%(round(max(y),3),round(min(y),3))) plt.plot(x,y1, label="T=2,ymax=%s,ymin=%s"%(round(max(y1),3),round(min(y1),3))) plt.plot(x,y2, label="T=4,ymax=%s,ymin=%s"%(round(max(y2),3),round(min(y2),3))) plt.grid() plt.legend(loc="best") plt.ylabel("x(n)") plt.xlabel("n") plt.show()

程序的结果：

由于迭代周期加倍，

（ ）

$x_ {n + 1} = rx_ {n}（1-x_ {n}）$ 广为人知。当增长率的值超过r = 3.56时 ，周期的倍数加速，并且在r = 3.57时已经出现了极端混乱。为了显示混乱的开始，我们使用以下程序：

程式码

 # -*- coding: utf8 -*- import matplotlib.pyplot as plt from numpy import * print(" nr=3,57 ") M=zeros([1041,1]) a= [3.57] for j in arange(0,1,1): M[0,j]=0.5 for j in arange(0,1,1): for i in arange(1,1041,1): M[i,j]=a[j]*M[i-1,j]*(1-M[i-1,j]) for i in arange(0,1041,1): if 1000<=i<=1015: print(" {0: 7.0f} {1: 7.4f}" . format(i,M[i,0])) x=arange(999,1040,1) y=M[999:1040,0] plt.title('     r=3,57') plt.plot(x,y) plt.grid() plt.ylabel("x(n)") plt.xlabel("n") plt.show()

程序的结果：

  nr=3,57 1000 0.4751 1001 0.8903 1002 0.3487 1003 0.8108 1004 0.5477 1005 0.8844 1006 0.3650 1007 0.8275 1008 0.5096 1009 0.8922 1010 0.3434 1011 0.8050 1012 0.5604 1013 0.8795 1014 0.3784 1015 0.8397

我们将编写一个程序来可视化迭代行为对增长参数r的依赖性。对于间隔中的每个r值

$a \ leqslant r \ leqslant b$ 执行1000次迭代以实现稳定性。然后，沿着垂直轴绘制作为迭代结果获得的每250个值，形成点（ r，x ）：

程式码

 # -*- coding: utf8 -*- import matplotlib.pyplot as plt from numpy import* N=1000 y=[] y.append(0.5) for r in arange(2.8,4.0,0.0001): for n in arange(1,N,1): y.append(round(r*y[n-1]*(1-y[n-1]),4)) y=y[N-250:N] x=[r ]*250 plt.plot( x,y, color='black', linestyle=' ', marker='.', markersize=1) plt.title("   2,8<= r<=4,0,0<=x<=1") plt.xlabel("r") plt.ylabel("y") plt.axvline(x=3.01,color='black',linestyle='--') plt.axvline(x=3.45, color='black',linestyle='--') plt.axvline(x=3.6,color='black',linestyle='--') plt.axvline(x=3.7,color='black',linestyle='--') plt.axvline(x=3.8,color='black',linestyle='--') plt.axvline(x=3.9,color='black',linestyle='--') plt.show()

结果以图表形式：

生成的图称为“分支图” ，它使您可以确定给定的r值是对应于周期还是混沌。人口规模的唯一价值确定为

约

$r \约3$ 然后周期为2到

约

$r \约3.4$ ，然后是周期为4的周期，然后是周期为8的周期，然后迅速接近混乱。

应该注意的是，图中未填充空间的垂直区域是r = 3.6和r = 3.7 ，位于r = 3.7和r = 3.8之间， r = 3.8和r = 3.9之间。循环顺序从先前的混乱中返回。
考虑周期为3 in的周期的出现

$3.8 \ leqslant r \ leqslant $ 3.$ 对上一个程序进行更改：

程式码

 # -*- coding: utf8 -*- import matplotlib.pyplot as plt from numpy import* N=1000 y=[] y.append(0.5) for r in arange(3.8,3.9,0.0001): for n in arange(1,N,1): y.append(round(r*y[n-1]*(1-y[n-1]),4)) y=y[N-250:N] x=[r ]*250 plt.plot( x,y, color='black', linestyle=' ', marker='.', markersize=1) plt.title("   3,8<= r<=3,9,0<=x<=1") plt.xlabel("r") plt.ylabel("y") plt.axvline(x=3.83,color='black',linestyle='--') plt.show()

程序的结果：

周期3的周期出现在点r = 3.83的附近，然后依次分为周期6,12,24。具有周期3的周期的存在意味着存在任何其他有限周期的周期，以及根本没有任何周期的混沌周期。

分支图使您可以通过平滑更改参数来跟踪系统的开发。使用固定的参数值，蜘蛛图（Lamera图）可以跟踪点轨道。

蜘蛛图的构造使您可以识别在分支图上不可见的各种效果。让我们编写一个程序：

程式码

 # -*- coding: utf8 -*- import matplotlib.pyplot as plt from numpy import * a=2.7 x1=0.62 def ff(x): return a*x*(1-x) b=a*x1*(1-x1)/x1 def fl(x): return b*x x=0.1 y=0 Y=[] X=[] for i in arange(1,30,1): X.append(x) Y.append(y) y=ff(x) X.append(x) Y.append(y) x=y/b plt.title('   \n  λx(1-x)  λ = 2.7') plt.plot(X,Y,'r') x1=arange(0,1,0.001) y1=[ff(x) for x in x1] y2=[fl(x) for x in x1] plt.plot(x1,y1,'b') plt.plot(x1,y2,'g') plt.grid(True) plt.show()

Lamera图：

机械系统的周期加倍

考虑一个微分方程，该方程对非线性弹簧上给定质量的材料点的自由阻尼振动进行建模，在非线性弹簧上，阻尼由速度确定。

$mx ^ {''} + cx ^ {'} + kx + \ beta x ^ {3} = 0$ （6）

在等式（6）中，项kx表示施加到给定质量的材料点上的线性弹簧的力，而项

$\ beta x ^ {3}$ 代表弹簧的实际非线性。

如果力作用于自由振动系统（6），则通过Duffing微分方程描述强制振动所施加的质量的物质点的位移：

$mx ^ {''} + cx ^ {'} + kx + \ beta x ^ {3} = F_ {0} cos \ omega t$ （7）

方程（7）包含在其中的大多数参数都通过数字求解。图中显示了根据方程式（7）的数学模型的机械系统：

给定系统的一个特征是，使用了一根柔性金属线代替弹簧，该金属线在垂直平面内振荡，对此钩常数k为负。在该方案中，稳定平衡点（a）和（c），以及不稳定平衡点（b）。

当一个实质点从位置（b）移开时，作用在其上的力就会排斥。如果例如由振荡磁场产生的周期性力被空气阻力部分衰减。然后，方程（7）是具有以下参数范围的材料点的水平位移x（t）的可接受的数学模型

$k <0，c> 0，\ beta> 0$ 。

为了研究这种非线性系统的行为，我们采取

$k = -1，m = c = \ beta = \ omega = 1$ 那么微分方程（7）的形式为：

$x ^ {''} + x ^ {'}-x + x ^ {3} = F_ {0} cos（t）$ ，（8）

我们编写了一个程序，用于在初始条件下对方程（8）进行数值积分

$x（0）= 1，x ^ {'}（0）= 0$ 在外地

$100 \ leqslant t \ leqslant 200$ 对于以下每个振幅值

$F_ {0} = 0.6; 0.7; 0.75; 0.8$ ，并分别绘制平面的解

$x（t），x ^ {'}（t）$ 和

$t，x（t）$ ：

程式码

 # -*- coding: utf8 -*- from numpy import * from scipy. integrate import odeint import matplotlib.pyplot as plt for F in [0.6,0.7,0.75,0.8]: def f(y,t): y1,y2=y return [y2,-y2-y1**3+y1+F*cos(t)] t=arange(100,200,0.001) y0=[1.0,0.0] [y1,y2]=odeint(f, y0, t, full_output=False,rtol=1e-12).T if F==0.6: plt.subplot(221) plt.title('  F=0.6,T=2'r'$\pi$') plt.plot(y1,y2, color='black', linestyle=' ', marker='.', markersize=0.1) plt.grid(True) plt.subplot(222) plt.title(' x(t): F=0.6,T=2'r'$\pi$') plt.plot(t,y1, color='black', linestyle=' ', marker='.', markersize=0.1) plt.grid(True) elif F==0.7: plt.subplot(223) plt.plot(y1,y2, color='black', linestyle=' ', marker='.', markersize=0.1, label='  \n F=0.7,T=4'r'$\pi$') plt.legend(loc='upper left') plt.grid(True) plt.subplot(224) plt.plot(t,y1, color='black', linestyle=' ', marker='.', markersize=0.1, label=' x(t): F=0.7,T=4'r'$\pi$') plt.legend(loc='upper left') plt.grid(True) plt.show() if F==0.75: plt.subplot(221) plt.title('  F=0.75,T=8'r'$\pi$') plt.plot(y1,y2, color='black', linestyle=' ', marker='.', markersize=0.1) plt.grid(True) plt.subplot(222) plt.title(' x(t): F=0.75,T=8'r'$\pi$') plt.plot(t,y1, color='black', linestyle=' ', marker='.', markersize=0.1) plt.grid(True) elif F==0.8: plt.subplot(223) plt.plot(y1,y2, color='black', linestyle=' ', marker='.', markersize=0.1, label=' \n F=0.8,') plt.legend(loc='upper left') plt.grid(True) plt.subplot(224) plt.plot(t,y1, color='black', linestyle=' ', marker='.', markersize=0.1, label=' x(t): F=0.8,') plt.legend(loc='upper left') plt.grid(True) plt.show()

该程序产生的图表

从周期加倍到混沌的这种转变显示了非线性机械系统响应于相应物理参数变化的一般行为，例如：

$k，m，c，\ beta，\ omega，F_ {0}$ 。这种现象在线性机械系统中不会发生。

吸引人洛伦兹

代入Duffing方程进行强迫振荡（7）会导致二维非线性微分方程系统，如上列表所示。 E.N.考虑了应用于气象问题的三维非线性微分方程组。洛伦兹：

$\ frac {dx} {dt} =-sx + sy，$

$\ frac {dy} {dt} =-xz + rx-y，$ （9）

$\ frac {dz} {dt} = xy-dz$

最好将系统（9）的解决方案投影到三个平面之一上。我们针对参数b = \ frac {8} {3}，s = 10，r = 28，初始条件x（0）=-8，y（0）= 8，z（0）= 27的值编写一个数值积分程序：

程式码

 # -*- coding: utf8 -*- import numpy as np from scipy.integrate import odeint import matplotlib.pyplot as plt s,r,b=10,28,8/3 def f(y, t): y1, y2, y3 = y return [s*(y2-y1), -y2+(r-y3)*y1, -b*y3+y1*y2] t = np.linspace(0,20,2001) y0 = [-8, 8, 27] [y1,y2,y3]=odeint(f, y0, t, full_output=False).T plt.plot(y1,y3, color='black', linestyle=' ', marker='.', markersize=2) plt.xlabel('x') plt.ylabel('z') plt.grid(True) plt.title("     xz") plt.show()

程序的结果：

考虑到随时间变化的曲线图上的图像，可以假定点P（x（t），y（t），z（t））产生随机数的左右振动。对于Lorenz系统的气象应用，在随机数个晴天之后，随后是随机数的雨天。

考虑一个用于在初始条件略有不同的情况下在xyz平面上绘制Lorentz吸引子的程序：

程式码

 # -*- coding: utf8 -*- import numpy as np from scipy.integrate import odeint import matplotlib.pyplot as plt from mpl_toolkits.mplot3d import Axes3D #     . s,r,b=10,25,3 def f(y, t): y1, y2, y3 = y return [s*(y2-y1), -y2+(r-y3)*y1, -b*y3+y1*y2] #        t = np.linspace(0,20,2001) y0 = [1, -1, 10] [y1,y2,y3]=odeint(f, y0, t, full_output=False).T fig = plt.figure(facecolor='white') ax=Axes3D(fig) ax.plot(y1,y2,y3,linewidth=2) plt.xlabel('y1') plt.ylabel('y2') plt.title(" : y0 = [1, -1, 10]") y0 = [1.0001, -1, 10] [y1,y2,y3]=odeint(f, y0, t, full_output=False).T fig = plt.figure(facecolor='white') ax=Axes3D(fig) ax.plot(y1,y2,y3,linewidth=2) plt.xlabel('y1') plt.ylabel('y2') plt.title(" : y0 = [1.0001, -1, 10]") plt.show()

下图显示了程序的结果：

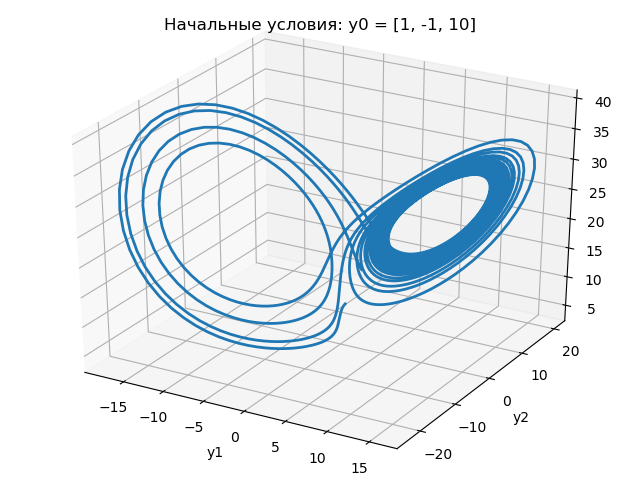
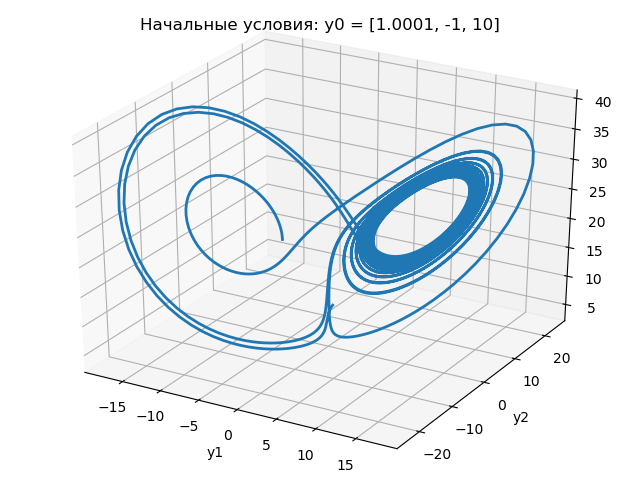
从以上图表可以看出，初始条件从1.0更改为1.0001会极大地改变Lorentz吸引子的变化性质。

罗斯勒系统

这是一个非常深入研究的非线性三维系统：

$\ frac {dx} {dt} =-y-z，$

$\ frac {dy} {dt} = x- \ alpha y，$ （10）

$\ frac {dz} {dt} = b + x（x-c）$

我们将为初始参数x（0）= 0，y（0）= 0，z（0）= 0的以下条件下的参数a = 0.39，b = 2，c = 4编写一个用于系统（10）的数值积分的程序：

程式码

 # -*- coding: utf8 -*- import numpy as np from scipy.integrate import odeint import matplotlib.pyplot as plt a,b,c=0.398,2.0,4.0 def f(y, t): y1, y2, y3 = y return [(-y2-y3), y1+a*y2, b+y3*(y1-c)] t = np.linspace(0,50,5001) y0 = [0,0, 0] [y1,y2,y3]=odeint(f, y0, t, full_output=False).T plt.plot(y1,y2, color='black', linestyle=' ', marker='.', markersize=2) plt.xlabel('x') plt.ylabel('y') plt.grid(True) plt.title("     xy") plt.show()

程序的结果：

在飞机上，Rossler的磁带看起来像个圈，但在太空中却像Moebius磁带一样被扭曲。

结论

为了演示混乱的现象，我们提供了一种使用高级Python编程语言编写的简单直观的程序，可以轻松升级到该主题的新项目。本文着重教育和方法论方面的知识，可以在学习过程中使用。

参考文献

关于混乱及其创建方法的一些知识
审视洛伦兹吸引子
FPGA混沌发生器
微分方程和边值问题：使用Mathematica，Maple和MATLAB进行建模和计算。第三版。来自英语 -M .: LLC“ I.D. 威廉姆斯（Williams），2008年。-1104羽。 -Paral。山雀。英文

混沌的数学模型

引言

以生物种群数量增长为例，将周期和混乱时期加倍

机械系统的周期加倍

吸引人洛伦兹

罗斯勒系统

结论

参考文献

More articles: