最近,该
材料发表在Quanta杂志上,其中作者谈到了一种现象,从数学家的经验不足的读者的角度来看,这是令人惊讶的。 其本质是某种类型的几乎所有多项式都是不可约的,也就是说,它们不能分解。 该证明适用于许多纯数学领域。 但这对于现代生活的支柱之一-数字加密也是个好消息。
为了可靠地存储数字信息,广泛使用了使用RSA算法的加密。 这是该计划的简化版本,即使是七年级学生也可以想到与朋友交换消息:每个字母都分配有一个数字,再乘以一个预先确定的秘密密钥。 要解密消息,只需将其划分为密钥即可。
RSA加密的工作方式与此类似。 我们给出一个非常简化的解释。 用户想到一条消息并对其执行某些数学运算,包括乘以非常大的数字(几百个数字长)。 解密消息的唯一方法是找到结果*的简单因素。
*数字的素数是需要乘以得到该数字的素数。 因此,对于数字12,它是2 * 2 * 3,对于数字495,它是3、3、5和11。
RSA加密的安全性是基于这样一个事实,即数学不知道找到大量素数的快速方法。 而且,如果加密的消息不是给您的,并且您没有解密它的密钥,那么尝试找到此密钥可能需要花费数千年的时间。 此外,对于大多数现代计算机也是如此,在这些计算机的帮助下,仍然不可能选择正确的简单因素。
但是有一种解决方法。
每个数字都可以表示为唯一的代数方程。 并且,与寻找数的素因不同,寻找多项式的素因要容易得多。 并且一旦将多项式分解为这样的素因数,该信息就可以用于搜索原始数的素因数。
运作方式如下。
第一步:选择您需要找出其主要因素的任何数字。 为简单起见,将数字15记下。
第二步: 15转换为二进制:
1111。
第三步:通过将所有二进制数转换为多项式的系数,此二进制表达式变为多项式:
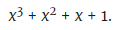
(注意:如果x = 2,则此多项式为15。数字2是二进制系统的基数。)
第四步:将多项式分解:
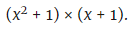 步骤五:将
步骤五:将 x = 2代入以下每个因子:
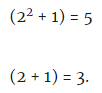 结论:
结论: 5和3是15的主要因子。
是的,这是一种查找诸如15之类的少数简单因素的过于复杂的方法,这些因素很容易在头脑中弄清楚。 但是,当涉及由数百个数字组成的大量数字时,此多项式方法具有惊人的优势。 为了分解素数,不存在快速算法。 但是有这样的算法可以分解大多项式。 因此,一旦您设法将一个大数转换为一个大多项式,您将非常接近找到该数的简单因子。
这是否意味着RSA加密存在风险? 不完全是 与此相关的是一种最近证明的关于多项式的新模式。
剑桥大学的数学家
Emmanuel Brulya和
Peter Varju证明,随着系数为0和1的多项式变长,它们完全可以扩展的可能性变小。 而且,如果多项式无法分解,则无法将其用于搜索需要计算数量的简单因数。
Brull和Varju的证据实际上表明,破解RSA加密的解决方法无济于事。 RSA中使用的非常大的数字对应于非常长的多项式。 剑桥大学的科学家认为,找到这样可分解的长度的多项式几乎是不可能的。 长期以来,密码学家和数学家都怀疑这是事实。 但是,当世界网络安全性取决于使用某种数学技术的可能性时,总是有证据证明该技术确实无效。
