🔥 👨🏿‍🚀 🤐 双四元数 🥌 👨🏼‍🎨 🤠

如果打开本文，您可能已经听说过四元数，甚至可能在设计中使用它们。但是是时候提高到更高的水平了-双四元数。

本文提供有关双四元数及其基本操作的基本概念。为了更好地理解使用双四元数，显示了一个使用Canvas的Javascript清晰示例。

双四元数

双四元数是一个维数为8的超复数。在英语文章和文学作品中，它们被称为“双四元数”。在俄语文学中，它们也被称为“双四元数”或“复四元数”。

与四元数的主要区别在于四元数描述了物体在空间中的方向，而双四元数也描述了物体在空间中的位置。

双四元数可以表示为两个四元数：

开 始 ，

$\ widetilde {\ textbf {q}} = \开始{bmatrix} \ textbf {q} _1 \\ \ textbf {q} _2 \ end {bmatrix}，$

$\ textbf {q} _1$ -实部，确定物体在空间中的方向；

$\ textbf {q} _2$ -对偶部分，确定对象在空间中的位置。

双四元数也称为复数四元数，在这种情况下，它表示为四元数，四元数的每个组成部分都是双数（不要与复数混淆）。双重号码

$A = a_1 + \ epsilon a_2$ 在哪里

$a_1$ 和

$a_2$ 是实数，并且

$\ epsilon$ -具有属性的Clifford符号（复杂度）

$\ epsilon ^ 2 = 0$ 。由于我们对应用部分更感兴趣，因此我们不会深入研究数学，因此，我们将把双四元数视为两个四元数。

双四元数的几何解释

与四元数类似，您可以使用它来设置对象的方向，双四元数也可以设置位置。即双四元数一次设置两个值-对象在空间中的位置和方向。如果我们在动力学中考虑它们，那么双四元数定义了两个量-运动的线速度和物体旋转的角速度。下图显示了双四元数的几何含义。

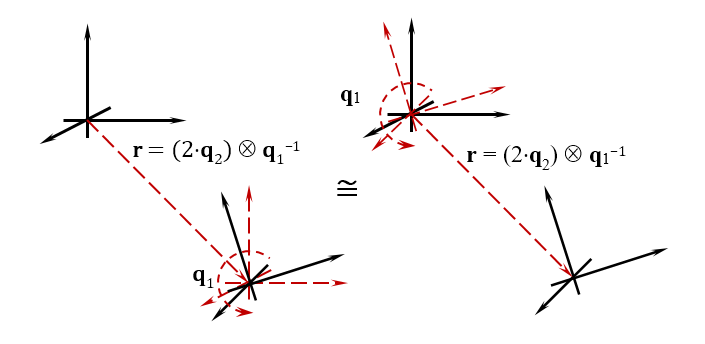
游戏开发人员知道，要确定对象在游戏空间中的位置和方向，将使用旋转矩阵和位移矩阵，并且根据应用它们的顺序，对象最终位置的结果会有所不同。对于习惯于将运动分为单独的操作的人，请接受使用双四元数规则：首先移动对象，然后旋转它。实际上，尽管使用复杂的超复杂结构，但您使用单个数字描述了这两个运动。

标量特性

考虑主要的标量特性。在此有必要注意以下事实：它们返回的不是普通实数，而是对偶数。

1.双四元数的规范

$\ | \ widetilde {\ textbf {q}} = \ | \ textbf {q} _1 \ | + \ epsilon（q_ {1_0} q_ {2_0} + \ textbf {q} _1 ^ T \ textbf {q} _2）$

2.双四元数模块

$| \ widetilde {\ textbf {q}} | = | \ textbf {q} _1 | + \ epsilon \ frac {q_ {1_0} q_ {2_0} + \ textbf {q} _1 ^ T \ textbf {q} _2} {| \ textbf {q} _1 |}$

基本操作

考虑使用双四元数的基本操作。如您所见，它们与四元数的相似操作非常相似。

1.双四元数配对

$\ widetilde {\ textbf {q}} ^ * = \开始{bmatrix} \ textbf {q} _1 ^ * \\ \ textbf {q} _2 ^ * \ end {bmatrix}$

2.双四元数加减法

$\ widetilde {\ textbf {q}} \ pm \ widetilde {\ textbf {p}} = \开始{bmatrix} \ textbf {q} _1 \ pm \ textbf {p} _1 \\ \ textbf {q} _2 \ pm \ textbf {p} _2 \ end {bmatrix}$

双四元数的加减运算是可交换的（术语可以互换）。

3.实数乘以双四元数

$a \ widetilde {\ textbf {q}} = \ widetilde {\ textbf {q}} a = \ begin {bmatrix} a \ textbf {q} _1 \\ a \ textbf {q} _2 \ end {bmatrix}$

4.双四元数乘法

$\ widetilde {\ textbf {q}} \ otimes \ widetilde {\ textbf {p}} = \ begin {bmatrix} \ textbf {q} _1 \ otimes \ textbf {p} _1 \\ \ textbf {q} _1 \ otimes \ textbf {p} _2 + \ textbf {q} _2 \ otimes \ textbf {p} _1 \ end {bmatrix}$

双四元数乘法是不可交换的（随着因子顺序的变化，双四元数乘法的结果是不同的）。

此操作是处理双四元数时的主要操作之一，并具有物理意义，即双四元数相乘的结果是将两个双四元数的旋转和线性运动相加的运算。

5.反向双四元数

$\ widetilde {\ textbf {q}} ^ {-1} = \ frac {\ widetilde {\ textbf {q}} ^ *} {\ | \ widetilde {\ textbf {q}} \ |}$

通过方向角和位置矢量确定双四元数

首先，我们定义坐标系统，其中将考虑物体在空间中的方向和位置。必须执行此操作以指定双四元数的实部（方向四元数），其旋转顺序会从方向角度影响生成的四元数。在这里，我们将由飞机的角度引导-偏航

$\ psi$ 音高

$\ vartheta$ 滚

$\伽玛$ 。

定义基本坐标系。想象一下，您正站在地球表面，并朝北看。

点O _o-坐标系的原点，位于对象的原点。
轴O _o Y _g-垂直向上指向，并且与重力矢量的方向相反。
轴O _o X _g-沿着局部子午线的切线指向北。
轴O _o Z _g-向右补充系统，并向右指向东方。

第二坐标系已连接。想象一下，例如飞机或其他物体。
O点-坐标系的原点通常位于对象质心的点。
OY轴-垂直向上并垂直于对象的水平面。
轴OX-指向对象的前端。
OZ轴-在右侧补充系统。

对象在空间中的位置由关联坐标系相对于固定基础坐标系的原点（点O ）的半径向量确定。关联坐标系相对于基础的方向由三个连续的打开决定：

偏航角

$\ psi$ -绕OY轴旋转，
俯仰角

$\ vartheta$ -绕OZ轴旋转，
横摆角

$\伽玛$ -绕轴OX旋转。

为了初步确定双四元数，必须指定双四元数的实数部分和对数部分。使用方向角相对于某个基本坐标系设置对象的方向和位置

$\ psi，\ vartheta，\ gamma$ 质心的位置向量

$r =（r_x，r_y，r_z）^ T$ 。

真正的部分

$\ textbf {q} _1$ 可以使用以下公式设置：

$\ textbf {q} _1 = \开始{bmatrix} \ cos \ frac {\ psi} {2} \ cos \ frac {\ vartheta} {2} \ cos \ frac {\ gamma} {2}＆-＆\ sin \ frac {\ psi} {2} \ sin \ frac {\ vartheta} {2} \ sin \ frac {\ gamma} {2} \\ \ cos \ frac {\ psi} {2} \ cos \ frac { \ vartheta} {2} \ sin \ frac {\ gamma} {2}＆+＆\ sin \ frac {\ psi} {2} \ sin \ frac {\ vartheta} {2} \ cos \ frac {\ gamma} {2} \\ \ cos \ frac {\ psi} {2} \ sin \ frac {\ vartheta} {2} \ sin \ frac {\ gamma} {2}＆+＆\ sin \ frac {\ psi} { 2} \ cos \ frac {\ vartheta} {2} \ cos \ frac {\ gamma} {2} \\ \ cos \ frac {\ psi} {2} \ sin \ frac {\ vartheta} {2} \ cos \ frac {\ gamma} {2}＆-＆\ sin \ frac {\ psi} {2} \ cos \ frac {\ vartheta} {2} \ sin \ frac {\ gamma} {2} \ end {bmatrix}$

请注意，如果轮换顺序不同，则表达式也将不同。

双重部分

$\ textbf {q} _2$ 由表达式定义：

$\ textbf {q} _2 = \ frac12 \ textbf {r} \ otimes \ textbf {q} _1$

从双四元数计算取向角和位置矢量。逆变换

取向角可以从双四元数的实部计算得出

$\ textbf {q} _1$ ：

$\ psi = \ arctan {\ frac {2（q_0 q_2-q_1 q_3）} {q_0 ^ 2 + q_1 ^ 2-q_2 ^ 2-q_3 ^ 2}}$

$\ vartheta = \ arcsin {（2（q_1 q_2 + q_0 q_3））}$

$\ gamma = \ arctan {\ frac {2（q_0 q_1-q_2 q_3）} {q_0 ^ 2-q_1 ^ 2 + q_2 ^ 2-q_3 ^ 2}}$

对象的位置由以下表达式确定：

$\ textbf {r} = 2 \ textbf {q} _2 \ otimes \ textbf {q} _1 ^ {-1}$

结果是四元数形式的向量

$\ textbf {r} =（0，r_x，r_y，r_z）^ T$

旋转并移动矢量双四元数

双四元数的一大特性是向量从一个坐标系到另一个坐标系的旋转和运动。设O _o X _g Y _g Z _g为固定基坐标系， OXYZ为对象的连接坐标系。然后，可以通过双四元数指定对象相对于基本坐标系的方向和位置

$\ widetilde {\ textbf {q}}$ 。如果指定了向量

$\ textbf {r}$ 在连接的坐标系中，那么你可以得到一个向量

$\ textbf {r} _0$ 在基本坐标系中使用以下公式：

$\ textbf {r} _0 = \ widetilde {\ textbf {q}} \ otimes \ textbf {r} \ otimes \ widetilde {\ textbf {q}} ^ {-1}$

并返回：

$\ textbf {r} = \ widetilde {\ textbf {q}} ^ {-1} \ otimes \ textbf {r} _0 \ otimes \ widetilde {\ textbf {q}}$

在哪里

$\ textbf {r}$ 是双四元数形式的向量，

$\ textbf {r} =（1、0、0、0、0、0，r_x，r_y，r_z）$

Biquaternion JavaScript库

上面所有带有双四元数的操作都在javascript库中实现，根据您的任务，可以使用其他编程语言来实现。使用双四元数的主要功能：

功能介绍	内容描述
`DualQuaternion.dq`	双四元数体由8个数字组成的数组
`DualQuaternion(dq0, dq1, dq2, dq3, dq4, dq5, dq6, dq7)`	通过指定所有八个数字来定义双四元数的构造函数
`DualQuaternion.fromEulerVector(psi, theta, gamma, v)`	通过使用Euler角设置对象的方向和对象的位置矢量来获取双四元数
`DualQuaternion.getEulerVector()`	从双四元数获得欧拉角和位置向量
`DualQuaternion.getVector()`	从biquaternion获取位置向量
`DualQuaternion.getReal()`	获取双四元数的实部（确定对象在空间中的方向）
`DualQuaternion.getDual()`	获取双四元数的对偶部分（确定对象在空间中的位置）
`DualQuaternion.norm()`	将双四元数范数作为双数获取
`DualQuaternion.mod()`	将biquaternion模块作为双数获取
`DualQuaternion.conjugate()`	获取共轭双四元数
`DualQuaternion.inverse()`	获取反向双四元数
`DualQuaternion.mul(DQ2)`	双四元数乘法
`DualQuaternion.toString()`	例如，将双四元数转换为字符串，以输出到调试控制台

文件dual_quaternion.js

 /** * * Author 2017, Akhramovich A. Sergey (akhramovichsa@gmail.com) * see https://github.com/infusion/Quaternion.js */ // 'use strict'; /** * Dual Quaternion constructor * * @constructor * @returns {DualQuaternion} */ function DualQuaternion(dq0, dq1, dq2, dq3, dq4, dq5, dq6, dq7) { if (dq0 === undefined) { this.dq = [1, 0, 0, 0, 0, 0, 0, 0]; } else { this.dq = [dq0, dq1, dq2, dq3, dq4, dq5, dq6, dq7]; } return this; }; //         DualQuaternion['fromEulerVector'] = function(psi, theta, gamma, v) { var q_real = new Quaternion.fromEuler(psi, theta, gamma); var q_v = new Quaternion(0, v[0], v[1], v[2]); var q_dual = q_v.mul(q_real); return new DualQuaternion( q_real.q[0], q_real.q[1], q_real.q[2], q_real.q[3], q_dual.q[0]*0.5, q_dual.q[1]*0.5, q_dual.q[2]*0.5, q_dual.q[3]*0.5); }; DualQuaternion.prototype = { 'dq': [1, 0, 0, 0, 0, 0, 0, 0], /** *    (psi, theta, gamma)      */ 'getEulerVector': function() { var euler_angles = this.getReal().getEuler(); var q_dual = this.getDual(); var q_dual_2 = new Quaternion(2.0*q_dual.q[0], 2.0*q_dual.q[1], 2.0*q_dual.q[2], 2.0*q_dual.q[3]); var q_vector = q_dual_2.mul(this.getReal().conjugate()); return [euler_angles[0], euler_angles[1], euler_angles[2], q_vector.q[1], q_vector.q[2], q_vector.q[3]]; }, /** *       */ 'getVector': function() { var euler_vector = this.getEulerVector(); return [euler_vector[3], euler_vector[4], euler_vector[5]]; }, /** *     * @returns {Quaternion} */ 'getReal': function() { return new Quaternion(this.dq[0], this.dq[1], this.dq[2], this.dq[3]); }, /** *     * @returns {Quaternion} */ 'getDual': function() { return new Quaternion(this.dq[4], this.dq[5], this.dq[6], this.dq[7]); }, /** *   * !   ! */ 'norm': function() { return [Math.pow(this.dq[0], 2) + Math.pow(this.dq[1], 2) + Math.pow(this.dq[2], 2) + Math.pow(this.dq[3], 2), this.dq[0]*this.dq[4] + this.dq[1]*this.dq[5] + this.dq[2]*this.dq[6] + this.dq[3]*this.dq[7]]; }, /** *   * !   ! */ 'mod': function() { var q_real_mod = Math.sqrt(Math.pow(this.dq[0], 2) + Math.pow(this.dq[1], 2) + Math.pow(this.dq[2], 2) + Math.pow(this.dq[3], 2)); return [q_real_mod, (this.dq[0]*this.dq[4] + this.dq[1]*this.dq[5] + this.dq[2]*this.dq[6] + this.dq[3]*this.dq[7])/q_real_mod]; }, /** *   * DQ' := (dq0, -dq1, -dq2, -dq3, dq4, -dq5, -dq6, -dq7) */ 'conjugate': function() { return new DualQuaternion(this.dq[0], -this.dq[1], -this.dq[2], -this.dq[3], this.dq[4], -this.dq[5], -this.dq[6], -this.dq[7]); }, //    'inverse': function() { var q_real_norm = new Quaternion(this.dq[0], this.dq[1], this.dq[2], this.dq[3]).norm(); var dq_norm_inv = [q_real_norm, - (this.dq[0]*this.dq[4] + this.dq[1]*this.dq[5] + this.dq[2]*this.dq[6] + this.dq[3]*this.dq[7])/q_real_norm]; var dq_conj = this.conjugate(); //      return new DualQuaternion( dq_norm_inv[0] * dq_conj.dq[0], dq_norm_inv[0] * dq_conj.dq[1], dq_norm_inv[0] * dq_conj.dq[2], dq_norm_inv[0] * dq_conj.dq[3], dq_norm_inv[0] * dq_conj.dq[4] + dq_norm_inv[1] * dq_conj.dq[0], dq_norm_inv[0] * dq_conj.dq[5] + dq_norm_inv[1] * dq_conj.dq[1], dq_norm_inv[0] * dq_conj.dq[6] + dq_norm_inv[1] * dq_conj.dq[2], dq_norm_inv[0] * dq_conj.dq[7] + dq_norm_inv[1] * dq_conj.dq[3]); }, /** *   * q1_real*q2_real, q1_real*q2_dual + q1_dual*q2_real */ 'mul': function(DQ2) { var q1_real = this.getReal(); var q1_dual = this.getDual(); var q2_real = DQ2.getReal(); var q2_dual = DQ2.getDual(); var q_res_real = q1_real.mul(q2_real); var q_res_dual_1 = q1_real.mul(q2_dual); var q_res_dual_2 = q1_dual.mul(q2_real); return new DualQuaternion( q_res_real.q[0], q_res_real.q[1], q_res_real.q[2], q_res_real.q[3], q_res_dual_1.q[0] + q_res_dual_2.q[0], q_res_dual_1.q[1] + q_res_dual_2.q[1], q_res_dual_1.q[2] + q_res_dual_2.q[2], q_res_dual_1.q[3] + q_res_dual_2.q[3]); }, /** *    */ 'transformVector': function (v) { var dq_res = this.mul(new DualQuaternion(1, 0, 0, 0, 0, v[0], v[1], v[2])).mul(this.conjugate()); return [dq_res.dq[5], dq_res.dq[6], dq_res.dq[7]]; }, /** *   ,   */ 'toString': function() { return '[' + this.dq[0].toString() + ', ' + this.dq[1].toString() + ', ' + this.dq[2].toString() + ', ' + this.dq[3].toString() + ', ' + this.dq[4].toString() + ', ' + this.dq[5].toString() + ', ' + this.dq[6].toString() + ', ' + this.dq[7].toString() + ']'; } } /* // TEST: var dq1 = new DualQuaternion.fromEulerVector(0 * Math.PI/180.0, 0 * Math.PI/180, 0 * Math.PI/180, [10, 20, 30]); console.log(dq1.toString()); console.log('getEulerVector = ', dq1.getEulerVector()); console.log('norm = ', dq1.norm()); console.log('mod = ', dq1.mod()); console.log('conjugate = ', dq1.conjugate().dq); console.log('inverse = ', dq1.inverse().dq); var dq2 = new DualQuaternion.fromEulerVector(0 * Math.PI/180.0, 0 * Math.PI/180, 0 * Math.PI/180, [10, 0, 0]); console.log('mul = ', dq1.mul(dq2).dq); console.log('transformVector ??? = ', dq1.transformVector([0, 0, 0])); */

使用双四元数的示例

为了更好地理解以双四元数为例的基本原理，请考虑做一个小游戏。设置了矩形区域-地图。一艘漂浮在地图上的船，装有安装在地图上的旋转喷枪。在此有必要考虑的是，对于船舶来说，基本坐标系是地图的坐标系，对于枪支来说，基本坐标系是船舶。所有对象都在地图坐标系中绘制，在这里，有趣的是如何使用biquaternion乘法属性从枪坐标系过渡到地图坐标系。船的移动由W，A，S，D键控制。枪的方向由鼠标光标设置。

船和枪有两种类别： Ship和Gun 。在船级的构造函数中，以biquaternion点的形式设置其形状，并以this.dq_pos biquaternion的形式this.dq_pos地图上的初始方向和位置。

双四元数增量也用于船舶控制。来回移动（键W，S）时，仅双四元数的对偶部分将发生变化；而控制左右键（键A，D）时，双四元数的实部和对偶部分将发生变化，从而设定了旋转角度。

 function Ship(ctx, v) { this.ctx = ctx; this.dq_pos = new DualQuaternion.fromEulerVector(0*Math.PI/180, 0, 0, v); //   this.dq_forward_left = new DualQuaternion.fromEulerVector(0, 0, 0, [ 15, 0, -10]); this.dq_forward_right = new DualQuaternion.fromEulerVector(0, 0, 0, [ 15, 0, 10]); this.dq_backward_left = new DualQuaternion.fromEulerVector(0, 0, 0, [-15, 0, -10]); this.dq_backward_right = new DualQuaternion.fromEulerVector(0, 0, 0, [-15, 0, 10]); this.dq_forward_forward = new DualQuaternion.fromEulerVector(0, 0, 0, [ 30, 0, 0]); //      this.dq_dx_left = new DualQuaternion.fromEulerVector( 1*Math.PI/180, 0, 0, [0, 0, 0]); this.dq_dx_right = new DualQuaternion.fromEulerVector(-1*Math.PI/180, 0, 0, [0, 0, 0]); this.dq_dx_forward = new DualQuaternion.fromEulerVector(0, 0, 0, [ 1, 0, 0]); this.dq_dx_backward = new DualQuaternion.fromEulerVector(0, 0, 0, [-1, 0, 0]); return this; };

在类本身中，只有一个函数可呈现Ship.draw()船。注意双四元数运算的应用，该运算将船舶的每个点与船舶当前位置和方向的双四元数相乘。

 Ship.prototype = { 'ctx': 0, 'dq_pos': new DualQuaternion.fromEulerVector(0, 0, 0, 0, 0, 0), /** *   */ 'draw': function() { //         v_pos = this.dq_pos.getVector(); v_forward_left = this.dq_pos.mul(this.dq_forward_left).getVector(); v_forward_right = this.dq_pos.mul(this.dq_forward_right).getVector(); v_backward_left = this.dq_pos.mul(this.dq_backward_left).getVector(); v_backward_right = this.dq_pos.mul(this.dq_backward_right).getVector(); v_forward_forward = this.dq_pos.mul(this.dq_forward_forward).getVector(); //   ctx.beginPath(); ctx.moveTo(v_backward_left[0], v_backward_left[2]); ctx.lineTo(v_forward_left[0], v_forward_left[2]); ctx.lineTo(v_forward_left[0], v_forward_left[2]); ctx.lineTo(v_forward_forward[0], v_forward_forward[2]); ctx.lineTo(v_forward_right[0], v_forward_right[2]); ctx.lineTo(v_backward_right[0], v_backward_right[2]); ctx.lineTo(v_backward_left[0], v_backward_left[2]); ctx.stroke(); ctx.closePath(); } };

在枪类的构造函数中，以双四元数点的形式指定其形状。喷枪将显示为一行。船上的初始方向和位置由this.dq_pos双this.dq_pos确定。同样，还设置了与安装它的船的绑定。船上的喷枪只能旋转，因此在控制喷枪时，双四元数的增量将仅更改双四元数的实部，从而设置旋转角度。在此示例中，机具由鼠标光标引导，因此枪支的旋转将立即发生。

 function Gun(ctx, ship, v) { this.ctx = ctx; this.ship = ship; //     this.dq_pos = new DualQuaternion.fromEulerVector(0, 0, 0, v); //   this.dq_forward = new DualQuaternion.fromEulerVector(0, 0, 0, [20, 0, 0]); this.dq_backward = new DualQuaternion.fromEulerVector(0, 0, 0, [ 0, 0, 0]); //     this.dq_dx_left = new DualQuaternion.fromEulerVector( 1*Math.PI/180, 0, 0, [0, 0, 0]); this.dq_dx_right = new DualQuaternion.fromEulerVector(-1*Math.PI/180, 0, 0, [0, 0, 0]); return this; };

在gun类中，也仅实现了其渲染Ship.draw()一个功能。枪显示为一条线，由这两个点this.dq_backward和this.dq_forward 。为了确定枪支点的坐标，使用了双四元数乘法。

 Gun.prototype = { 'ctx': 0, 'ship': 0, 'dq_pos': new DualQuaternion.fromEulerVector(0, 0, 0, [0, 0, 0]), /** *   */ 'draw': function() { //     v_pos = this.ship.dq_pos.getVector(); v_forward = this.ship.dq_pos.mul(this.dq_backward).mul(this.dq_forward).getVector(); v_backward = this.ship.dq_pos.mul(this.dq_backward).getVector(); //   ctx.beginPath(); ctx.moveTo(v_backward[0], v_backward[2]); ctx.lineTo(v_forward[0], v_forward[2]); ctx.stroke(); ctx.closePath(); } };

船炮控制处理是通过事件实现的。在主程序循环中处理的四个变量leftPressed, upPressed, rightPressed, downPressed负责按下和释放船舶控制键。

 leftPressed = false; rightPressed = false; upPressed = false; downPressed = false; dq_mouse_pos = new DualQuaternion.fromEulerVector(0, 0, 0, [0, 0, 0]); document.addEventListener("keydown", keyDownHandler, false); document.addEventListener("keyup", keyUpHandler, false); document.addEventListener("mousemove", mouseMoveHandler, false); //     function keyDownHandler(e) { if (e.keyCode == 37 || e.keyCode == 65 || e.keyCode == 97) { leftPressed = true; } //  A else if (e.keyCode == 38 || e.keyCode == 87 || e.keyCode == 119) { upPressed = true; } //  W else if (e.keyCode == 39 || e.keyCode == 68 || e.keyCode == 100) { rightPressed = true; } //  D else if (e.keyCode == 40 || e.keyCode == 83 || e.keyCode == 115) { downPressed = true; } //  S } //     function keyUpHandler(e) { if (e.keyCode == 37 || e.keyCode == 65 || e.keyCode == 97) { leftPressed = false; } //  A else if (e.keyCode == 38 || e.keyCode == 87 || e.keyCode == 119) { upPressed = false; } //  W else if (e.keyCode == 39 || e.keyCode == 68 || e.keyCode == 100) { rightPressed = false; } //  D else if (e.keyCode == 40 || e.keyCode == 83 || e.keyCode == 115) { downPressed = false; } //  S }

从使用双四元数操作的角度来看，最有趣的功能之一是沿鼠标指针的方向控制飞船的枪支。首先，在dq_mouse_pos双dq_mouse_pos元数中确定鼠标指针的坐标。然后，使用双四元数乘法计算鼠标相对于船只的位置的双四元数。船舶的双四元数取自鼠标双dq_mouse_pos_about_ship = ship_1.dq_pos.inverse().mul(dq_mouse_pos);元数dq_mouse_pos_about_ship = ship_1.dq_pos.inverse().mul(dq_mouse_pos);
（注意：顺序双四元数乘法运算从右到左读取）。最后，确定工具和鼠标矢量之间的角度。枪的起点gun_1.dq_backward分配了接收到的值。

 function mouseMoveHandler(e) { var relativeX = e.clientX - canvas.offsetLeft; var relativeY = e.clientY - canvas.offsetTop; //           if (relativeX > 0 && relativeX < canvas.width && relativeY > 0 && relativeY < canvas.height) { //    dq_mouse_pos = new DualQuaternion.fromEulerVector(0, 0, 0, [relativeX, 0, relativeY]); //      //  .       //     // DQ_ship^(-1) * DQ_mouse dq_mouse_pos_about_ship = ship_1.dq_pos.inverse().mul(dq_mouse_pos); //       q_gun_mouse = new Quaternion.fromBetweenVectors(gun_1.dq_forward.getVector(), dq_mouse_pos_about_ship.getVector()); dq_gun_mouse = new DualQuaternion(q_gun_mouse.q[0], q_gun_mouse.q[1], q_gun_mouse.q[2], q_gun_mouse.q[3], 0, 0, 0, 0); gun_1.dq_backward = dq_gun_mouse; // console.log(dq_gun_mouse.getEulerVector()); // console.log(relativeX + ' ' + relativeY + ' ' + gun_1.dq_forward.toString()); } }

在该程序的主体中， gun_1舰船和舰炮ship_1和gun_1对象，显示调试信息，并执行舰船控制处理。

 var canvas = document.getElementById("myCanvas"); var ctx = canvas.getContext("2d"); ship_1 = new Ship(ctx, [100, 0, 100]); gun_1 = new Gun(ctx, ship_1, [0, 0, 0]); function draw() { ctx.clearRect(0, 0, canvas.width, canvas.height); ship_1.draw(); gun_1.draw(); // Debug info ship_euler_vector = ship_1.dq_pos.getEulerVector(); ship_euler_vector[0] = ship_euler_vector[0]*180/Math.PI; ship_euler_vector[1] = ship_euler_vector[1]*180/Math.PI; ship_euler_vector[2] = ship_euler_vector[2]*180/Math.PI; ship_euler_vector = ship_euler_vector.map(function(each_element){ return each_element.toFixed(2); }); ship_dq = ship_1.dq_pos.dq.map(function(each_element){ return each_element.toFixed(2); }); gun_dq = ship_1.dq_pos.mul(gun_1.dq_backward).dq.map(function(each_element){ return each_element.toFixed(2); }); ctx.font = "8pt Courier"; ctx.fillText("Ship: " + ship_dq + " | psi, theta, gamma, vector:" + ship_euler_vector, 10, 20); ctx.fillText("Gun: " + gun_dq, 10, 40); //   if (leftPressed) { ship_1.dq_pos = ship_1.dq_pos.mul(ship_1.dq_dx_left); } if (rightPressed) { ship_1.dq_pos = ship_1.dq_pos.mul(ship_1.dq_dx_right); } if (upPressed) { ship_1.dq_pos = ship_1.dq_pos.mul(ship_1.dq_dx_forward); } if (downPressed) { ship_1.dq_pos = ship_1.dq_pos.mul(ship_1.dq_dx_backward); } requestAnimationFrame(draw); } draw();

归档文件的链接包含用于处理四元数和双四元数的库的完整代码，程序脚本本身以及index.html文件，可以在浏览器中本地打开它们以运行上述示例。

使用双四元数的示例

结论

您可能会有一个问题：为什么可以使用标准的工具来移动和旋转对象，但为什么要使用如此复杂的数学工具呢？主要优势之一是双四元数形式的书写效率更高，因为表达式展开后，所有具有双四元数的运算都是线性的。该视频“ 具有近似双四元数混合的几何蒙皮”显示了双四元数计算的效率比其他方法高得多。

我主要从英语来源获取有关使用双季铵盐的信息。
从国内文献中，我可以建议两本书：

切尔诺科夫尤里·尼古拉耶维奇。 四元数和双四元数模型和固体力学方法及其应用。运动的几何学和运动学。 -伟大的理论著作。
戈迪夫·瓦迪姆·尼古拉耶维奇。 四元数和双四元数在几何和力学中的应用。 -用更易理解的语言编写，并显示了在塑造弯曲空间结构的任务中的应用。

双四元数

双四元数

双四元数的几何解释

标量特性

基本操作

通过方向角和位置矢量确定双四元数

从双四元数计算取向角和位置矢量。 逆变换

旋转并移动矢量双四元数

Biquaternion JavaScript库

使用双四元数的示例

结论

More articles:

从双四元数计算取向角和位置矢量。逆变换