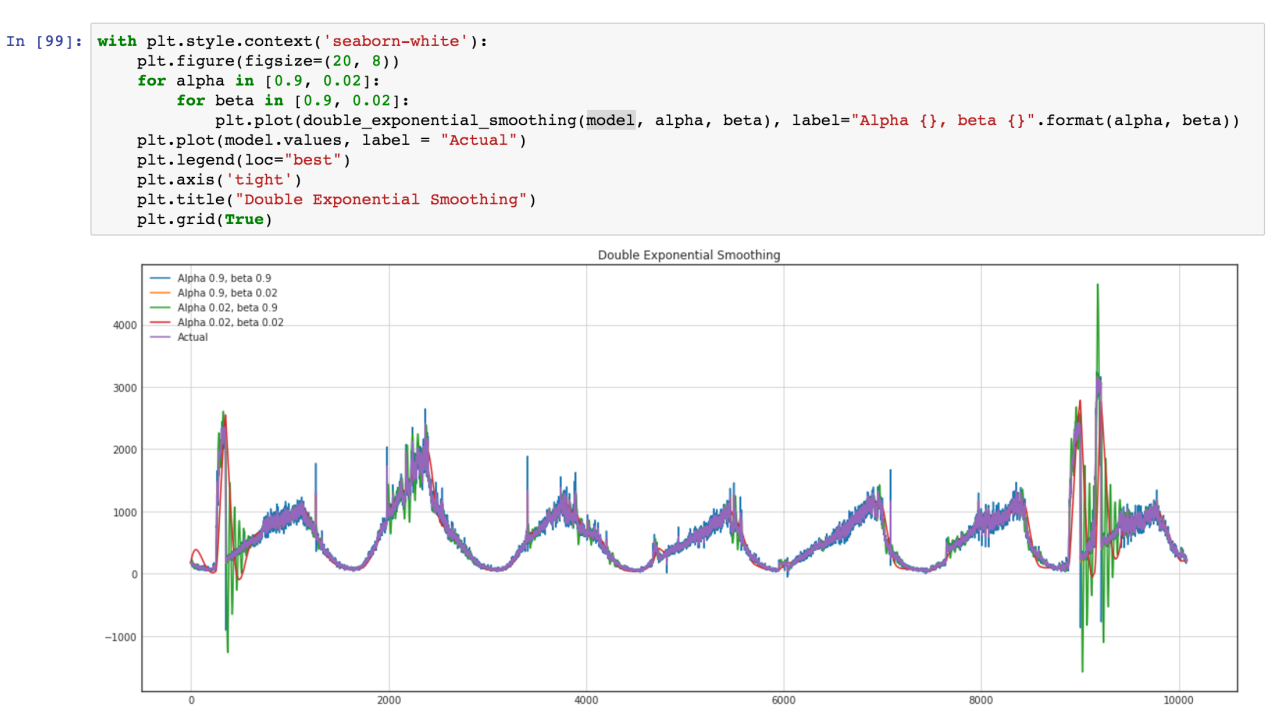
这是一篇简短的文章,介绍了了解时间序列及其背后的主要特征。
问题陈述
我们拥有每日和每周定期的时间序列数据。 我们想找到如何以最佳方式对数据建模的方法。

分析时间序列
时间序列的重要特征之一是平稳性。
在数学和统计中,平稳过程(即严格(完全)平稳过程或强(完全)平稳过程)是随机过程,其联合概率分布随时间推移而不会改变。
因此,诸如均值和方差之类的参数(如果存在)也不会随时间变化。 由于平稳性是在时间序列分析中使用的许多统计程序基础的假设,因此非平稳数据通常会转换为平稳的。
违反平稳性的最常见原因是平均值趋势,这可能是由于存在单位根或确定趋势。 在单位根的前一种情况下,随机冲击具有永久性影响,并且该过程不会恢复均值。 在确定性趋势的后一种情况下,该过程称为趋势平稳过程,随机冲击仅具有短暂的影响,该影响是均值回复的(即,均值返回其长期平均值,随着时间的推移,确定性会随时间变化)趋势)。
固定与非固定过程的示例
趋势线
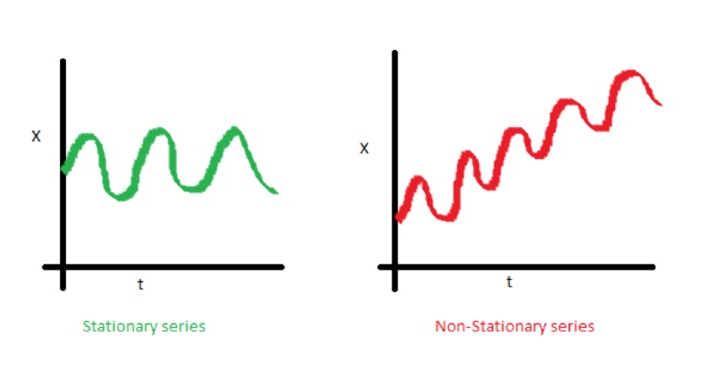
分散度
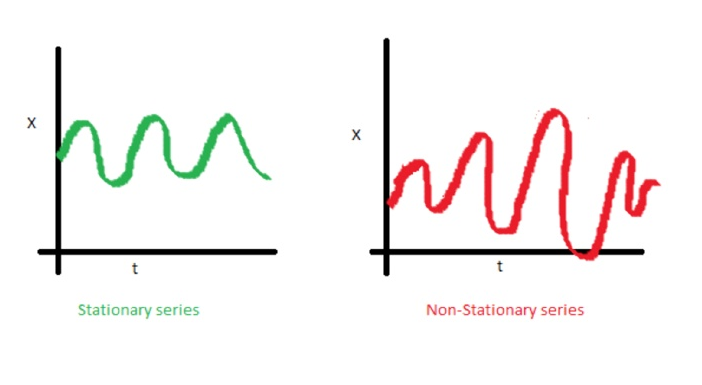
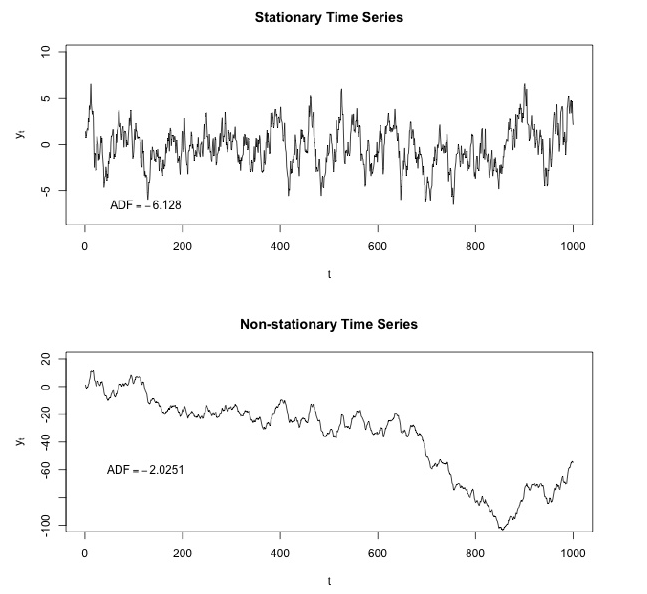
白噪声是随机的平稳过程,可以使用两个参数来描述:均值和色散(方差)。 在离散时间中,白噪声是离散信号,其采样被视为具有零均值和有限方差的一系列序列不相关的随机变量。
如果我们在y轴上投影,则可以看到正态分布。 白噪声是时间上的高斯过程。
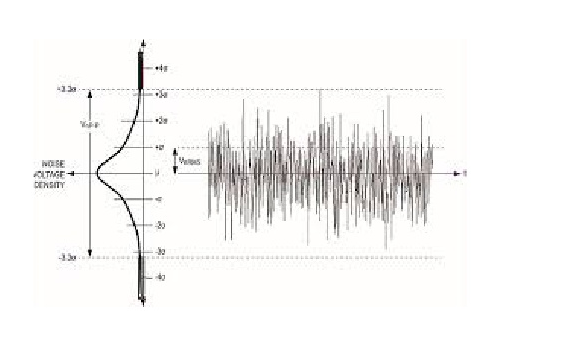
在概率论中,正态(或高斯)分布是一种非常常见的连续概率分布。 正态分布在统计中很重要,并且在自然科学和社会科学中经常用来表示其分布未知的实值随机变量。 由于中心极限定理,正态分布很有用。 它以最一般的形式表示,在某些条件下(包括有限方差),它表示从独立分布中独立得出的随机变量观测值样本的平均值在分布上收敛于正态分布,也就是说,当观测值数量达到正态分布时足够大。 预期为许多独立过程之和的物理量(例如测量误差)通常具有接近正态的分布。 此外,当相关变量呈正态分布时,许多结果和方法(例如不确定性的传播和最小二乘参数拟合)都可以以显式形式分析得出。
假设我们的数据有一定趋势。 围绕它的尖峰是由于许多随机因素影响了我们的数据。 例如,使用此方法很好地描述了服务请求的数量。 垃圾收集,高速缓存未命中,操作系统分页,很多因素都会影响服务响应的特定时间。 让我们从我们的数据中抽取半小时,从2017–08–27 12:00到12:30。 我们可以看到该数据具有趋势,并且有一些振荡
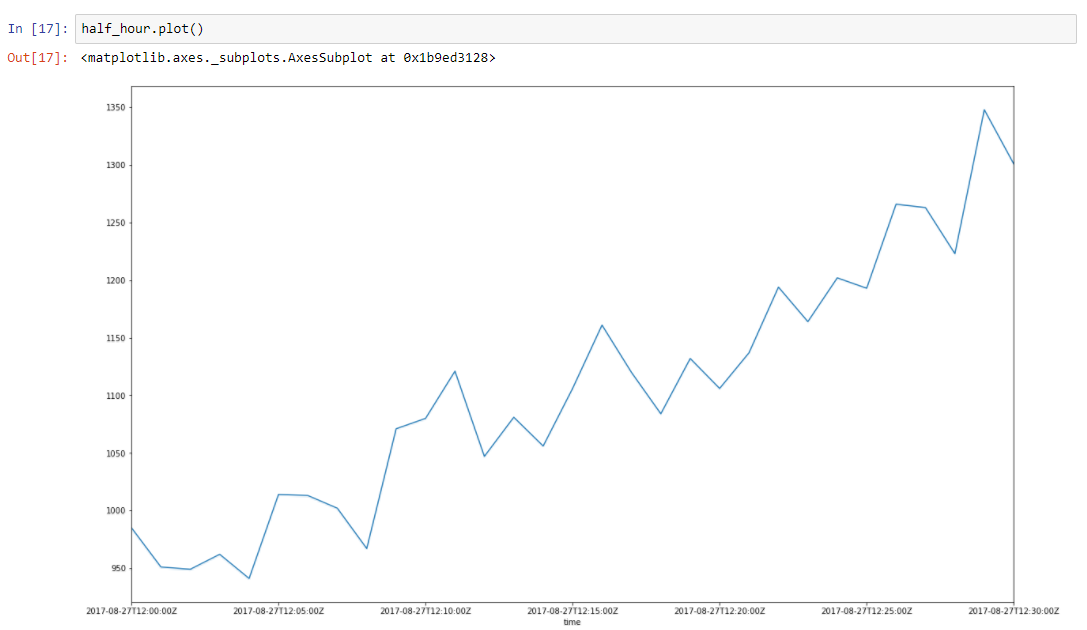
让我们构建回归线以定义该趋势线的斜率。
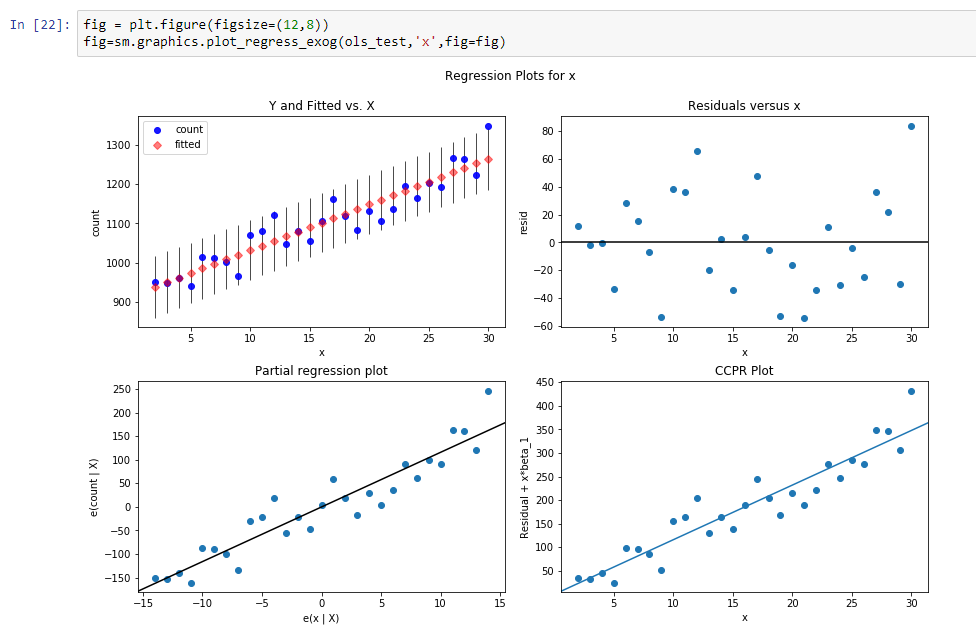
该回归的结果是:
const 916.269951dy / dx 11.599507结果意味着,const是该趋势线的水平,而dy / dx是一条斜线,其定义了水平随时间增长的速度。
因此,实际上我们将数据的维数从31个参数减少到2个参数。 如果从初始数据中减去回归函数值,我们将看到过程,该过程看起来像平稳的随机过程。
因此,减去后,我们可以看到趋势消失了,并且可以假定过程在此范围内是随机的。 但是我们如何确定。

让我们进行
Dickey – Fuller测试 。
迪基-富勒(Dickey)-富勒(Fuller)检验时间序列有根且也是平稳的零假设,或者拒绝该假设。 如果我们在初始切片上进行Dickey-Fuller测试,我们将得到
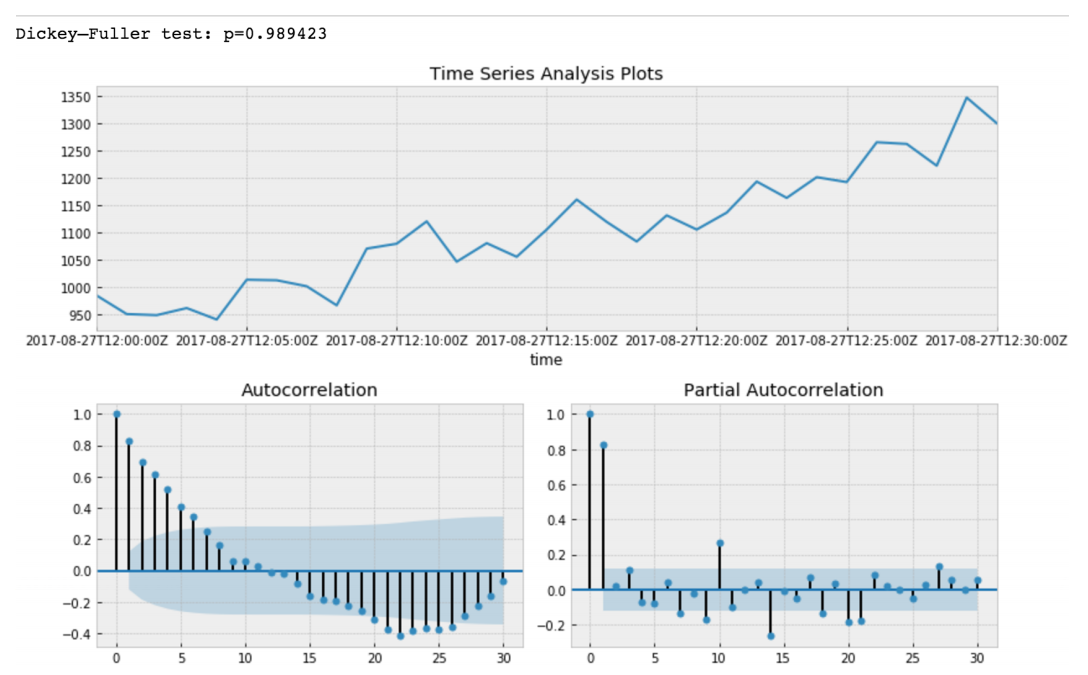
Dickey-Fuller检验的值非常有把握地拒绝零假设。 因此,我们的时间序列切片是非平稳的。 我们可以看到自相关函数显示了隐藏的自相关。
从原始数据中减去我们的回归模型后。

在这里,我们可以看到Dickey-Fuller检验值确实很小,并且没有拒绝关于时间序列切片的非平稳性的零假设。 自相关函数看起来也不错。
因此,我们对数据进行了一些转换,并且可以根据趋势线的斜率旋转数据。
数据的分段回归
分段回归 (也称为
分段回归或“折线回归”)是回归分析中的一种方法,其中将自变量划分为区间,并为每个区间拟合单独的线段。 通过对各种独立变量进行分区,也可以对多元数据执行分段回归分析。 当独立变量聚集到不同的组中时,在这些区域中的变量之间显示出不同的关系时,分段回归非常有用。 段之间的边界是断点。
实际上,由于我们无法考虑dx的度量点的恒定间隔,我们的斜率是非平稳时间序列的离散导数。 因此,我们可以将数据近似为使用时间序列回归趋势的离散导数计算的分段函数。

上面是2017年6月8日至8日的数据切片,直到08.00
看起来每个切片都有一个线性自相关,如果我们为每个切片找到一条回归线,则可以使用我们所做的假设来构建时间切片模型。
结果,我们将获得使用最少数量的参数描述的数据,这归因于更好的概括性。 Vapnik-Chervonenkis维度应尽可能小,以实现良好的概括。
在Vapnik – Chervonenkis理论中,VC维数(对于Vapnik – Chervonenkis维数)是可以通过统计分类算法学习的功能空间的容量(复杂性,表达能力,丰富性或灵活性)的度量。 它定义为算法可以破坏的最大点集的基数。 它最初由Vladimir Vapnik和Alexey Chervonenkis定义。
形式上,分类模型的能力与其复杂程度有关。 例如,考虑一个高阶多项式的阈值:如果多项式的评估结果大于零,则该点被分类为正,否则被分类为负。 高阶多项式可以摆动,因此可以很好地拟合给定的训练点集。 但是可以预料到分类器会在其他方面犯错误,因为它过于摇摆。 这样的多项式具有高容量。 一个更简单的选择是对线性函数进行阈值处理。 由于该功能的容量较低,因此可能无法很好地适应训练集。
因此,结果是我们使用分段回归近似了小时切片。
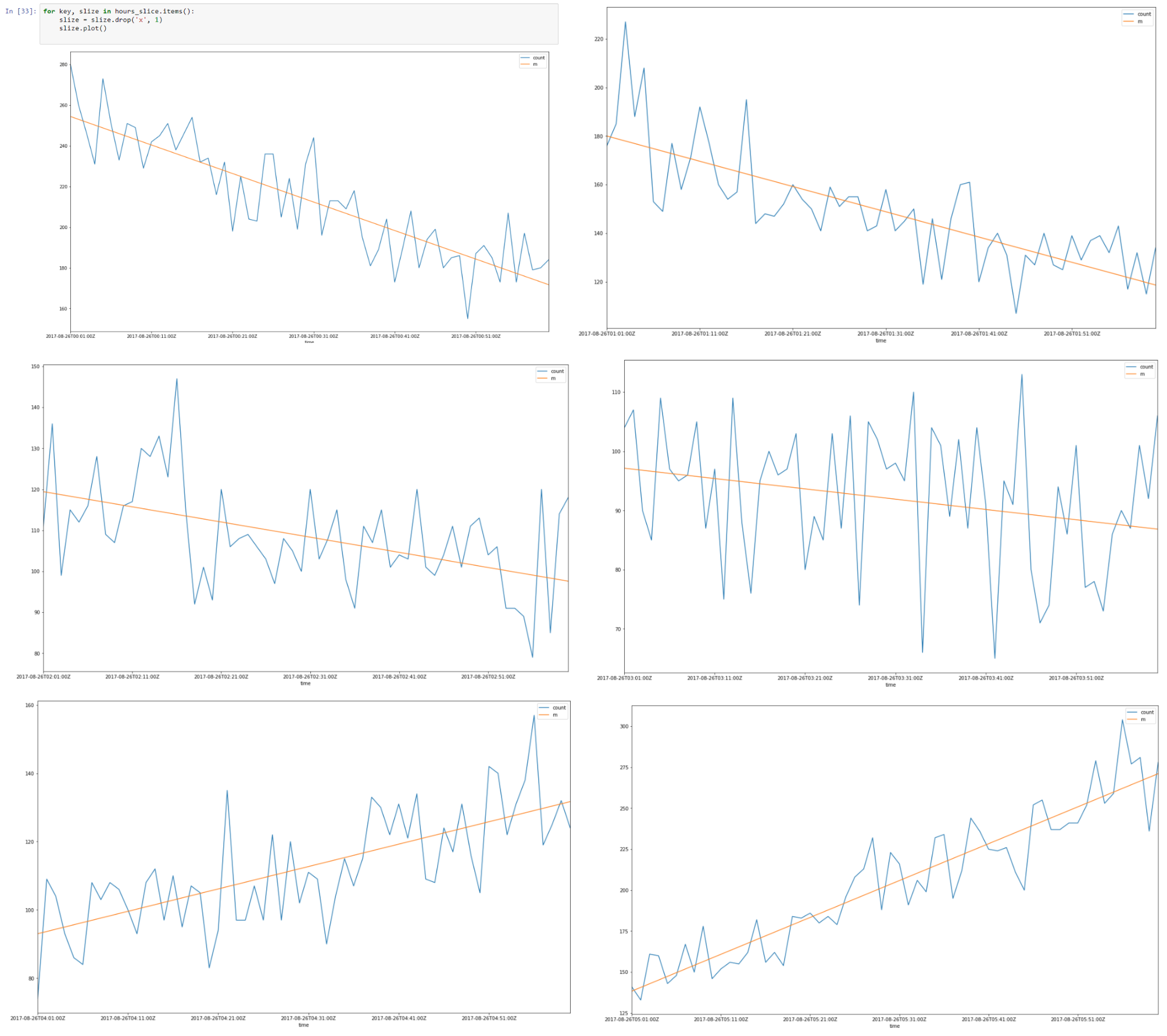
将所有8小时片放在一起

并通过减去回归模型使其变为平稳随机。
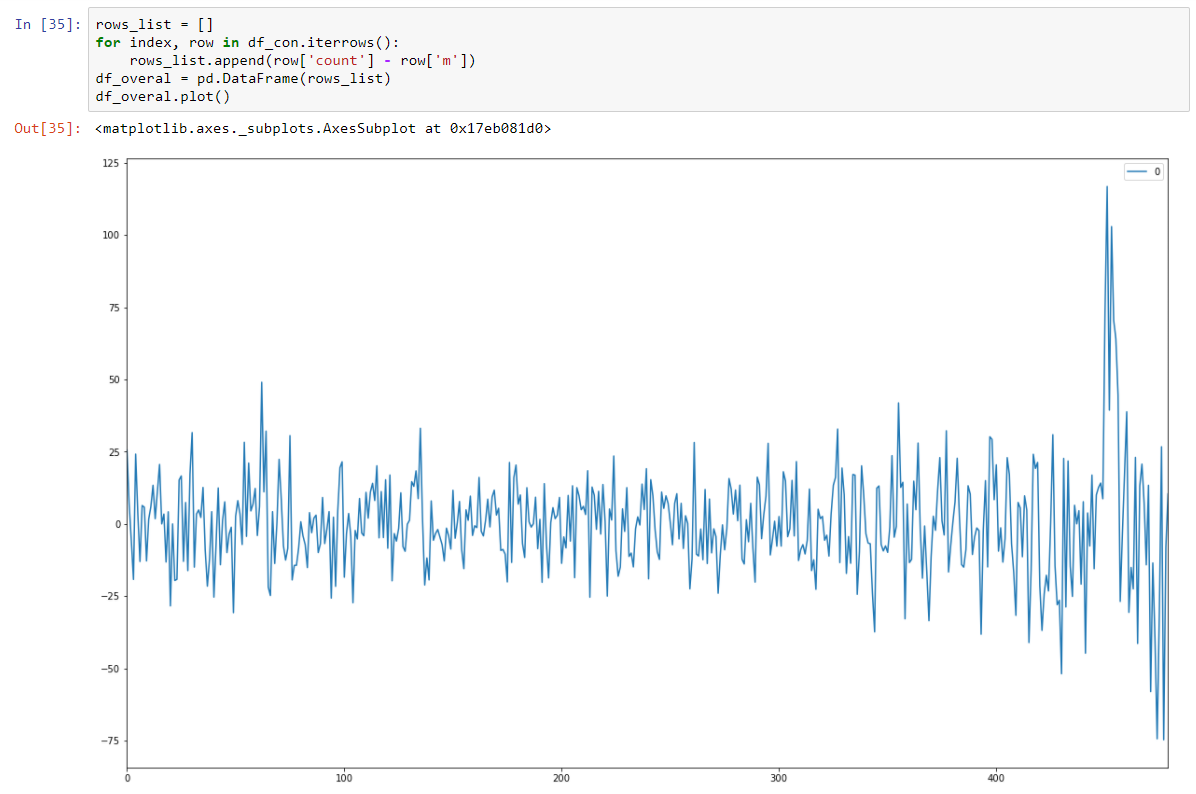
而且,我们对平稳的Dickey-Fuller测试非常有信心地表明,我们已将数据转换为平稳序列。
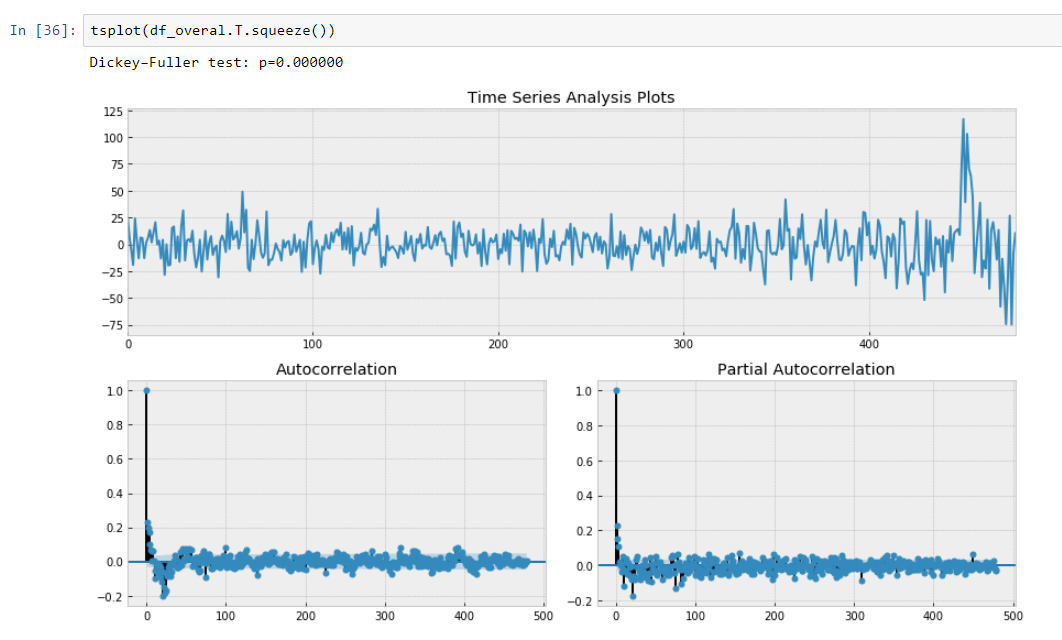
因此,我们有一个描述时间序列数据的预测模型。 我们将数据的维数减小了15/30倍!
实际上,我们应该返回模型预测的均值,并使用特定切片的水平和斜率将其转换回去。 对于模型预测,它将最小化平方误差之和。
但是我们也应该存储方差,因为方差的增加可能会导致出现新的未知因素,并且我们从领域知识中知道是这样。
因此,方差的快速变化也应引起注意。
我们也想使用ARIMA模型,但是更通用的方法更好,并且我们计划将这个模型与标准ARIMA进行比较以获得更好的结果。 让我们看一下时间序列(绿色是异常值上的方差爆发)