温馨提示
哈Ha! 我提请您注意
媒体上我的新文章的另一种翻译。
上次(
第一篇文章 )(
Habr ),我们使用Q-Learning技术创建了一个代理,该代理按模拟和真实的交换时间序列进行交易,并尝试检查此任务区域是否适合强化学习。
这次,我们将添加一个LSTM层,以考虑轨迹内的时间依赖性,并根据演示进行奖励整形。
让我提醒您,为了验证这一概念,我们使用了以下综合数据:
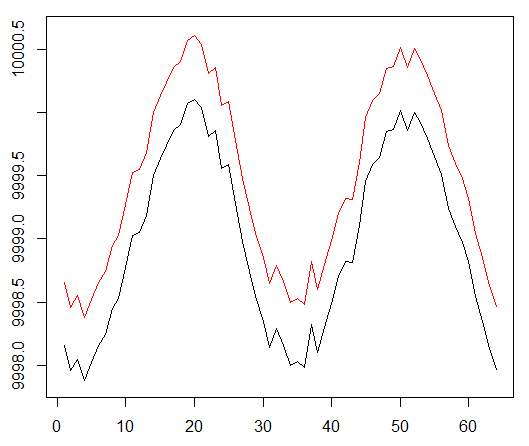
合成数据:正弦,白噪声。
正弦函数是第一个起点。 两条曲线模拟资产的购买和出售价格,其中价差是最小交易成本。
但是,这次我们要通过扩展信用分配路径来使此简单任务复杂化:
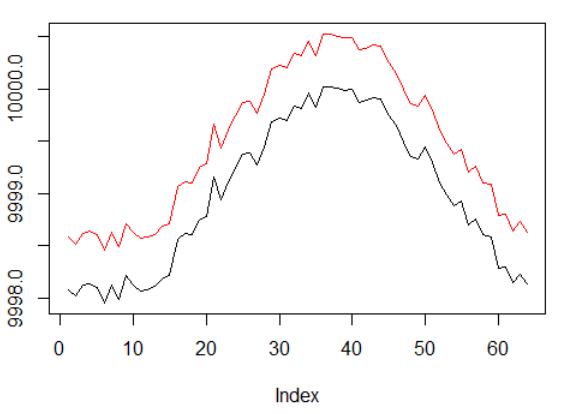
合成数据:正弦,白噪声。
窦相加倍。
这意味着我们使用的稀疏奖励必须分布在更长的轨迹上。 此外,由于代理商为了克服交易成本不得不执行2次以上的正确动作序列,因此,我们显着降低了获得正面奖励的可能性。 即使在诸如正弦波这样的简单条件下,这两个因素也极大地增加了RL的任务。
此外,我们还记得我们使用了这种神经网络架构:
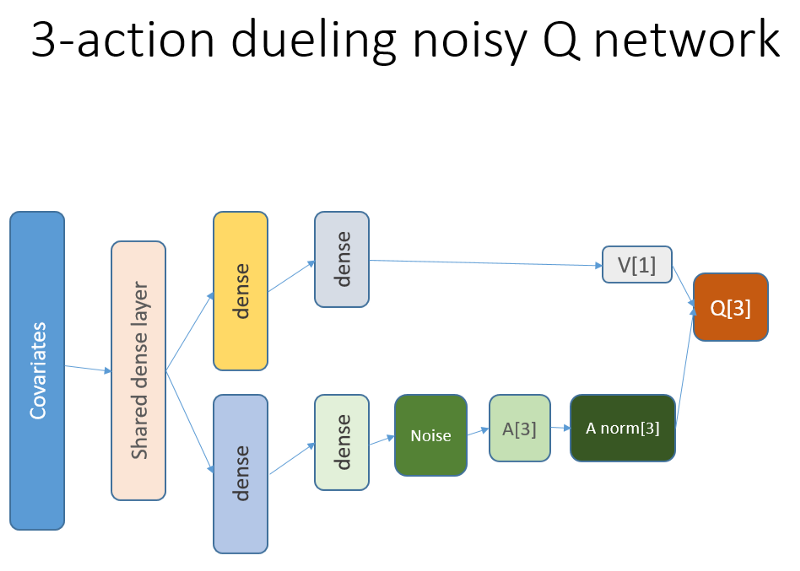
添加了什么,为什么
Lstm
首先,我们希望使代理对轨迹内的变化动态有更多的了解。 简而言之,代理人应该更好地了解自己的行为:他现在和过去的一段时间内所做的事情,以及国家行为的分配以及所获得的报酬如何发展。 使用递归层可以完全解决此问题。 欢迎使用用于启动一组新实验的新架构:

请注意,我对说明做了一些改进。 与旧的NN的唯一区别是第一个隐藏的LSTM层,而不是完全粘合的层。
请注意,在使用LSTM的情况下,我们必须更改用于训练的再现经验示例的选择:现在,我们需要过渡序列而不是单独的示例。 这是它的工作方式(这是算法之一)。 我们在以下步骤之前使用了点采样:

播放缓冲区的虚拟方案。
我们将此方案与LSTM结合使用:

现在选择序列(我们根据经验指定其长度)。
与以前一样,现在通过基于时空学习错误的优先级算法对样本进行调节。
LSTM循环级别允许从时间序列中直接传播信息,以拦截隐藏在过去滞后中的其他信号。 与我们有关的时间序列是一个二维张量,其大小为:表示我们的状态行为的序列的长度。
简报
屡获殊荣的工程,基于潜力的基于潜力的奖励塑造(PBRS)是一种功能强大的工具,可让您提高速度,稳定性,而又不违反解决我们环境的策略搜索过程的最优性。 我建议至少阅读该主题的原始文档:
people.eecs.berkeley.edu/~russell/papers/ml99-shaping.ps电位确定我们当前状态相对于我们要输入的目标状态的程度。 原理图:

经过反复试验,您可以理解一些选择和困难,我们省略了这些详细信息,使您无需做任何作业。
值得一提的是,可以通过演示来证明PBRS是合理的,这些演示是有关代理在环境中
几乎最佳行为的一种专家(或模拟)知识形式。 有一种方法可以使用优化方案为我们的任务找到此类演示文稿。 我们忽略了搜索的详细信息。
潜在奖励采用以下形式(等式1):
r'= r +伽玛* F(s')-F(s)
其中F是国家的潜力,r是初始奖励,gamma是折扣因子(0:1)。
基于这些想法,我们继续进行编码。在R中执行
这是基于Keras API的神经网络代码:
调试您的良心决定...
结果与比较
让我们深入研究最终结果。
注意:所有结果均为点估计,并且在多次运行中使用不同的随机种子sid可能会有所不同。比较包括:
- 没有LSTM和演示文稿的先前版本
- 简单的2元素LSTM
- 四元素LSTM
- 具有PBRS奖励的4单元LSTM
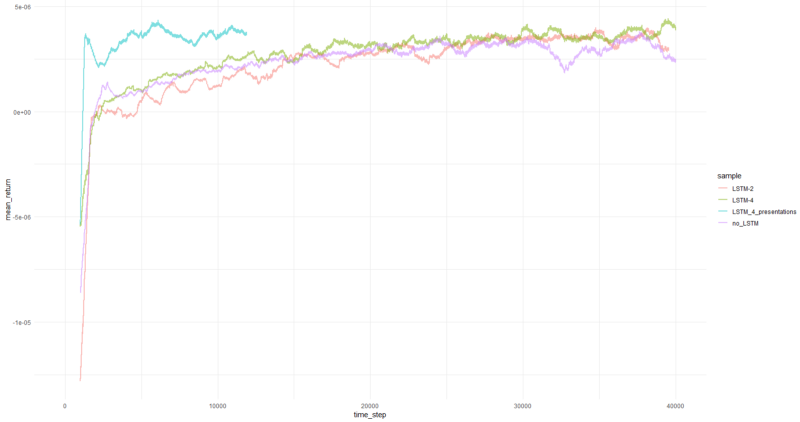
每集的平均回报平均超过1000集。
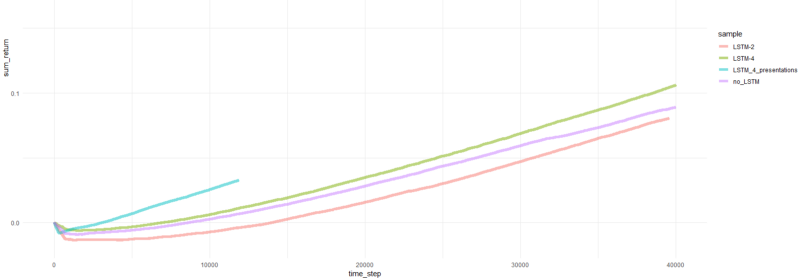
总剧集收益。
最成功的代理商的图表:

代理商绩效。
好吧,很明显,与以前的尝试相比,PBRS形式的代理收敛得如此迅速和稳定,因此可以被接受为重要的结果。 速度比没有演示文稿时快约4-5倍。 稳定性很棒。
使用LSTM时,4个单元的性能优于2个单元。 2单元LSTM的性能优于非LSTM版本(但是,这可能是单个实验的错觉)。
最后的话
我们已经看到,复发和能力建设的奖励是有帮助的。 我特别喜欢PBRS如此出色的表现。
不要相信有人让我说创建一个收敛良好的RL代理很容易,因为这是一个谎言。 添加到系统中的每个新组件都可能使其不稳定,并且需要大量配置和调试。
但是,有明确的证据表明,仅通过改进所使用的方法(数据保持不变)就可以改善问题的解决方案。 事实上,对于任何任务,一定范围的参数都比其他参数更好。 考虑到这一点,您正在走上成功的学习之路。
谢谢啦