再次预测，第2部分

今天，我将描述时间序列预测的其他一些属性。

即，具有片段相似性的变体的周期性和复杂性。



让我们回到上一篇文章的图表。 该图非常周期性（请参见下图），并且首先通过计算周期来预测它是正确的。 仅通过循环计算的使用，我就获得了4.1％的误差（映射）预测，而不是之前的实验点的5％。

在计算了周期之后，我们从图的初始值中减去周期的预测值，并且我们已经在尝试通过相关性预测最终的误差图。 结果，同一点我已经收到3.7％的错误。

该程序及其当前版本的源代码在此处 。 现在，它看起来更像是一个独立的序列预测实用程序，而不是测试一种方法和一张图表。 并且它可以对没有实际预测值的最后一点进行预测。

现在更多有关算法和含义的信息

猿 -绝对百分比误差- 绝对（预测事实）/事实
mape-平均绝对百分比误差

如果我们在这段时间内取一些猿猴并计算算术平均值，那么我们将得到mape。

就本身而言，未知图表的预测误差百分比几乎没有。 因为尚不清楚时间表通常会更改多少，因此尚不清楚它是否被预测太多。 从预测中比较地图是很方便的，该预测是基于下一个值将与最后一个已知值相同的假设而做出的。

对于实验点，该值为9.2％。 让我提醒您，这些数字是对前一天的预测。 即 日程安排中的波动为9.2％。 预测的结果是，该误差降低到3.7％。

这是几天研究图表的样子，每天波动很大：



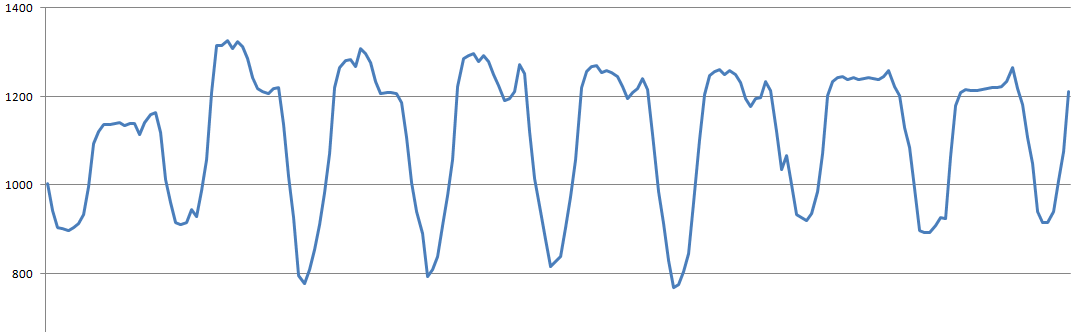
显然，如果这样的图被相关性折磨，则相关性将主要看到每日的波动，所有较小的细微差别将被淹没。

以下是对前一天的预测：



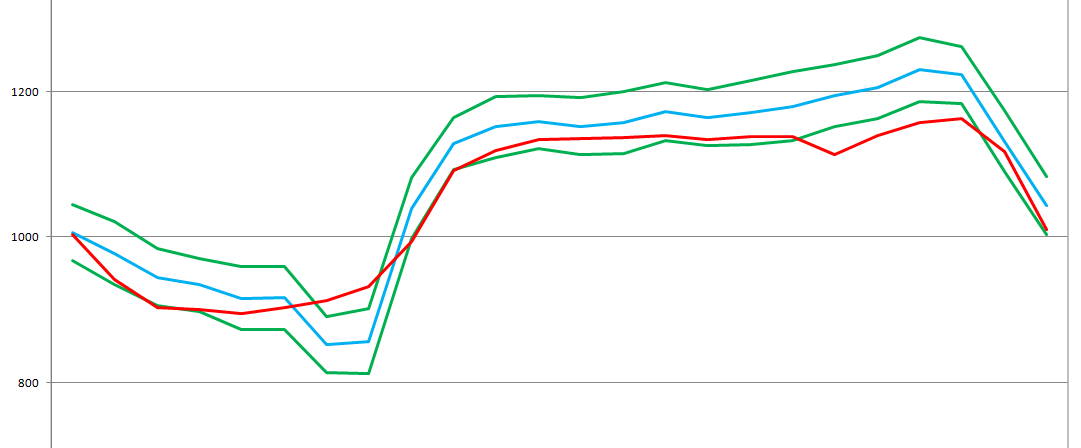
实际图形显示为红色，预测为蓝色，与中心的预测的三个标准差的边界为绿色-如果图形波动具有标准分布 ，则这将是可能图形走廊的99％。

周期计算

为了进行周期性预测，在文件cicling.h和cicling.cpp中组织了Cicling类。 此类对象累积N个媒体元素，其数量与循环的长度相对应。 平均值是根据可调整的公式累积的，它们称为移动平均值。

在我的解释中，该公式具有一定的调整长度，这比只是一个无意义的系数更方便。 该机制包含在dispersion.h和dispersion.cpp 文件的紧凑的MeanAdapt类中。

平均而言，该机制的实质如下：

cnt_vals = cnt_vals + 1; if (cnt_vals > cnt_adapt) su = su - su / (double)cnt_adapt + new_value; else su = su + new_value; mean = su / (double)min(cnt_vals, cnt_adapt); 

该类中仍然存在复杂性，对cnt_adapt的解释为负数，如果您有兴趣，请参阅源代码。

通常， Cicling类具有N个可调整平均值的元素，其中有当前元素，下一个值被添加到该元素，指针将移动到平均值的下一个元素。 当到达最后一个元素时，指针将移动到开头。 以此类推。 更精确地讲，该类只是做了ar_means [cnt_values％size_cicling] ，其中cnt_values是添加值的数量。

在将新值添加到当前平均值元素之前，从新值中减去当前平均值，从而生成误差值。 Cicling类可以递归地包含下一级别的循环Cicling * ne_level ，如果是这样，则将当前级别的错误传递给下一个周期，以总结下一个周期，否则返回错误。 对于当前图表，主要周期是每天-24小时和每周-168小时。

这会在所发送的实际值与循环平均值的当前值之间产生差异。 如果我们在相反的方向上对该机制应用零，并向其添加当前步骤的所有平均值，但仅在不修改MeanAdapt元素的情况下，我们将基于未来误差为零的假设来获得预测值。 我们将平均值的当前元素移至下一个，均不做任何修改，然后再次以相反的顺序馈入零。 结果是基于所有平均值之和的预测图。

对于这种机制，还有两个问题：如何确定可能的循环频率，以及如何确定最佳的适应时间。

我只是通过搜索测试数据来做到这一点。 该程序有一个用于扫描周期的按钮，该按钮可以扫描所有可能的周期周期，最大周期为2000，并从中找出最好的周期。

最好的循环将手动添加到“循环周期”字段中，下一次开始循环搜索时，将减去新添加的循环将其扫描。 仅当您检查当前图表时，默认情况下，最佳周期已在该字段中输入，并且不再存在。 因此，擦除它们并运行。

适应长度也可以通过穷举搜索来选择，但是您无需在任何地方指定它，因为程序每次启动都会再次扫描，因为 不长。 “周期周期”字段中指示周期的顺序也不重要，因为 在启动时，将选择最佳顺序。

像一切一样的周期。 考虑它们，从图中减去，我们得到误差图。

我实现的段相似度

此误差图表示波动，平均误差接近零-正负误差。 它可能包含相关性，也可能是剩余的随机成分。 段的相关性已经适用于它。

在这个问题上，我要说的是，按照皮尔逊的相关性来计算并不是最佳选择。 对此也有逻辑上的推理-这种相关性在不同图形强度的相似性下会增强，尽管具有不同强度，随后的行为完全并不意味着它将是相同的，而只是具有转移。 实际证据-应用周期性变量后，尝试应用Pearson相关只会使结果恶化。 同样，当不应用周期性应用时，其预后比周期性要差。

作为实验的结果，我得出的结论是，相似度的最佳计算方法是图之间的二次差。 如果该图已经是负循环，则该图将挂在零附近，仅它们之间的二次差就足够了。

如果不减去周期性，则二次方差更好，但要先减去平均值：



尽管我在这里写到这是段的相关性，但实际上是指它们之间的二次差。

在演示程序中，您可以选择我检查过的相似性/相关性的不同变体，并检查它们是否需要其他图形。 程序中相似度的计算由CorrSlide类在文件corr_slide.h和corr_slide.spp中实现 。 在CorrSlide :: Res方法CorrSlide :: get_res（...）中计算出不同的相似性公式。

除了上述不同的计算选项之外，此类还包括优化，因此您不必为以下所述的属性的相邻段重新计算计算。

我对每个位置都进行了扫描，扫描了许多不同的相关长度。 第一个长度取6点，第二个长度取两倍。 12，然后是下一个24，依此类推...对于每个长度，将这些段中最好的一组进行累积，并考虑平均预测和方差。 然后，从所有计数的包装（每个包装负责不同的长度）中选择最能预测当前点的包装。 预测方差最小的那个更好。

假设最长的段是最好的是不正确的。 首先，对于一个较长的细分，可能没有足够多的非常相似的细分，或者根本没有。 就像我在上一篇文章中提到的那样，采取最好的相似性是错误的。 其次，预测可以将更接近的值与预测点相关联，随后细分的扩展将不会给出更好的答案，而只会稀释带有不必要细分的最佳组合。

但是，据您所知，最短的细分市场并不是最好的细分市场。 结果，简单地收集了几包不同长度的相关段，并且看起来哪个包中的预测最明确-方差最小。

此外，他还可以选择随着值的显着性增加更接近于预测点来计算相似度。 在那里，长度每增加一倍，就会将两倍短的段添加两次。

还有一点关于排放

另外，他还制定了消除排放的机制。 原则上，排放实际上应被视为图表的元素或可能的误差。 但是必须在当前进度表的特征分布水平上考虑它们。 现在，我主要基于正确处理标准分布的原理进行计算。 因此，当前版本仅指示要排除的极端点。 它在“排放数量”字段中指示，并在计算中的多个点应用，这会明显扭曲结果。

而且，分布问题影响了预测系数，而我在上一篇文章中写到了该系数，但事实并非如此。 这些问题的分析留给程序的下一版本。

结果发生了什么

结果，所有这些多样性和丑陋性导致了以下事实：在减去周期性之后，可以更好地预测该图。

如果对此类段的长度尝试不同的选项，则预测的成功可能会有所不同。 即 结果不稳定。 如果我们在二次偏差中使用相似性，那么原则上，与皮尔森相关性相比，它总是在处理完循环后改善结果。 段的相似度长度是24的倍数（最小循环度）的使用，也会得到更好的结果。

计算速度足够快，您可以指定要计算一千个或更多的职位，并查看该细分的平均预测，并确保预测不仅在实验点成功。 尽管并非到处都如此醒目。

例如，对于1000个职位的时间段，将每一步的预测向前推1步，结果是：
所选期间的平均误差1.76473％
平均误差仅为1.78332％
假设预测为最后已知头寸，则为平均误差4.19216％

如果“预测位置数”字段保留为空白，则将从“日期/预测开始的位置/位置”到图表末尾的每个位置执行计算。

如果很有趣地看到我给出的相对于实验点的数字，那么在默认设置下，您需要将“预测位置数” = 1，“一个位置数” = 24更改。

值得注意的是，所有这些改进并未使欧元兑美元的预测变动最小。 看起来它完全独立于过去的历史。 尽管我仍将使用程序的下一版本进行检查。

如前所述，该程序具有通用性，您可以在其中选择数据文件，并在预测列和日期列（如果有的话）中指定它。 列分隔符可以是逗号或分号。 如果可能，该程序包含控件的描述。



该程序及其来源 。

现在，下次我将使用新属性来改善预测结果。