问题陈述

前几天，我在网上冲浪，一个很奇怪的事情引起了我的注意： Mendocino马达 。 它是一种极低摩擦的轴承转子：最初的转子有一个玻璃圆柱体挂在两个针上，而现代的则使用磁悬浮。 这是一种无刷发动机：转子上装有太阳能电池，可为缠绕在转子上的线圈产生电流。 转子在固定的磁场中旋转，太阳能电池一个接一个地暴露在光源下。 这是一个相当优雅的解决方案，非常有可能在家里重新创建。

这是解释其工作原理的视频（俄语）：


但是这部影片的好奇心比引擎本身还要强。 在视频说明中，德米特里·科列夫斯基（Dmitry Korzhevsky）写道： “您不能用磁铁代替侧支架！ 不要再问我这个了！”

免责声明：我不是物理学专家，在某些方面可能是非常错误的，因此欢迎进行更正。



让我们再次讨论转子的磁悬浮系统如何工作。 如果我们使用两个磁体，则取决于磁体之间的距离，潜在的等值线如下所示：



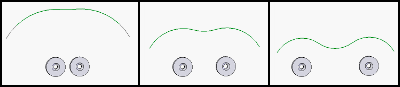
因此，我们在定子上放置了两个固定磁铁。 放置在转子轴上的磁铁不希望向侧面移动，因为等值线有一定的局部最小值。 相反，它将希望沿转子的轴弹出。 我们使用其中两个系统，最后，转子的轴在径向上是稳定的，但在横向上是不稳定的。 我们通过将转子倾斜到玻璃墙和倾斜的方式来解决此问题-我们具有低摩擦轴承。

但是玻璃墙有点……不美观，不是吗？ 逻辑上讲，我们希望将转子完全悬空在空中，而无需像这样的机械拐杖。 显然，德米特里（Dmitry）也遭到同样的问题轰炸，这就是为什么他不得不在描述中正确地指出这是不可能的。 我敢打赌，德米特里（Dmitry）并不是唯一一个对此感到厌倦的人。

让我们看看这一点，我引用：

如果基本磁铁按此图所示间隔并定向，会发生什么情况？ 它会在轴向平面内提供稳定性，并消除镜面要求吗？

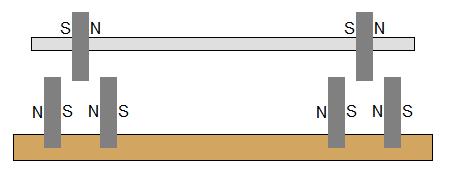
或者在这里 ，我引用：

在Mendocino电机上，为什么一侧自由浮动，而另一侧则向墙壁倾斜？ 我知道这个问题听起来微不足道，但是我已经弄清楚了为什么不使用与悬浮在一起的磁铁作为反作用力作用在轴的两侧的想法？ 我附上了我的意思的非常粗糙的jpg。 我指的是轴末端的绿色磁铁。 有什么理论或法律可以阻止这种情况吗？

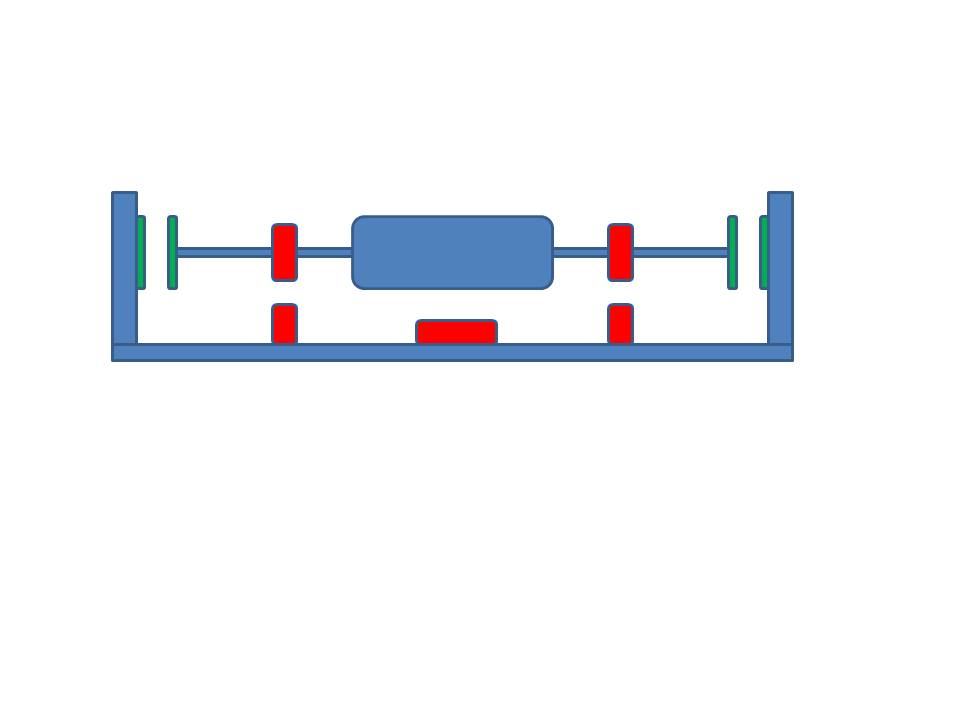
我们可以看到，世界上许多人都希望摆脱这种看起来不太机械的部分。 在上学的时候，我并没有给予太多的关注，所以对于一个完全稳定的磁悬浮系统而言，为什么根本不可行，这一点我都不是很清楚。 有一天，我在午餐会上问了我的主管，我的主管是一位世界闻名的科学家（应用数学而不是物理学）：“为什么不可能？” 你知道吗，他也不知道！

上面发布的论坛也没有为该问题提供适当的答案。 最好的情况是，有人提到了称为Earnshaw定理的东西，乍一看并不能帮助理解。 它指出：点电荷的集合不能仅通过电荷的静电相互作用而维持在稳定的静态平衡构型。 明白了吗 我当然没有。 假设我可以接受一个事实，那就是我们在谈论电荷而不是磁铁。 那呢

第一个插图

当我无法将头缠在某物上时，我倾向于画它。 为简单起见，让我们以2D方式进行说明。 想象一下，四个固定电荷以正方形放置，中间有一个免费电荷。 像这样：



那么，自由电荷不是平衡吗？ 无论它在哪里移动，它都接近固定电荷之一，从而增加了推力！ 让我们尝试绘制免费电荷的潜在能量图。 我错过了很多物理课，所以我的知识库是Wikipedia。 因此，如果您只有一个固定电荷，那么它将在其周围的电场中产生静电势 ：

真空中点电荷的静电势（或库仑势）方程：

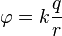
在我所有的思想实验中，所有系数均为0或1。因此，q电荷为1，未知k也为1。这意味着一个固定电荷产生的势能被测量为1 / r，其中r是与原子之间的距离。充电。

在我们的情况下，固定电荷场内的自由电荷的势能也等于1 / r。 （公平地说，能量等于k * q1 * q2 / r，但是我们选择系数使计算更容易）。 对于多个电荷，我们只需将所有电位相加即可。

让我们绘制免费充电的潜在能量图。 我为此使用鼠尾草 ：

var('x,y') def unit_potential(a,b,x,y): return 1/(sqrt((xa)^2 + (yb)^2)) def system_potential(x,y): return unit_potential(1,1,x,y)+unit_potential(-1,1,x,y)+unit_potential(1,-1,x,y)+unit_potential(-1,-1,x,y) contour_plot(system_potential(x,y), (x, -2, 2), (y, -2, 2), cmap='hsv', contours=30, region=5-system_potential(x,y), figsize=12, colorbar=True) 

有我们的地图。 白点（点）是势能无限大的地方：



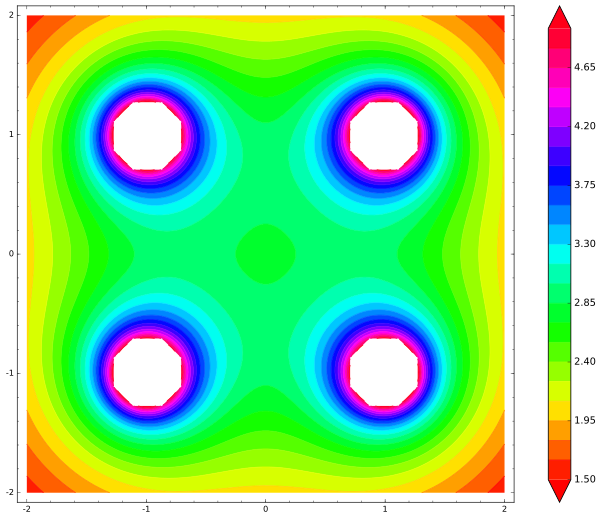
我们清楚地看到了中心的局部最小能量。 中心电荷想要移动到的任何地方，能量都会增加，因此小的干扰将迫使其返回中心-稳定平衡点。 那么，恩萧错了吗？ 不，他不是，我只是错误地画了插图。 这是问这个问题的人中的一个普遍错误。 现在停下来几分钟，然后猜测：我想念什么？

实际上，在这种情况下，错误是在二维空间中，固定电荷产生的势能测量为-ln r，其中r是到电荷的距离，而不是1 / r。 暂时说我的话，让我纠正方程式，而无需过多解释。 正确的代码如下所示：

 var('x,y') def unit_potential(a,b,x,y): return -ln(sqrt((xa)^2 + (yb)^2)) def system_potential(x,y): return unit_potential(1,1,x,y)+unit_potential(-1,1,x,y)+unit_potential(1,-1,x,y)+unit_potential(-1,-1,x,y) contour_plot(system_potential(x,y), (x, -2, 2), (y, -2, 2), cmap='hsv', contours=30, region=5-system_potential(x,y), figsize=12, colorbar=True) 

这是它生成的地图：



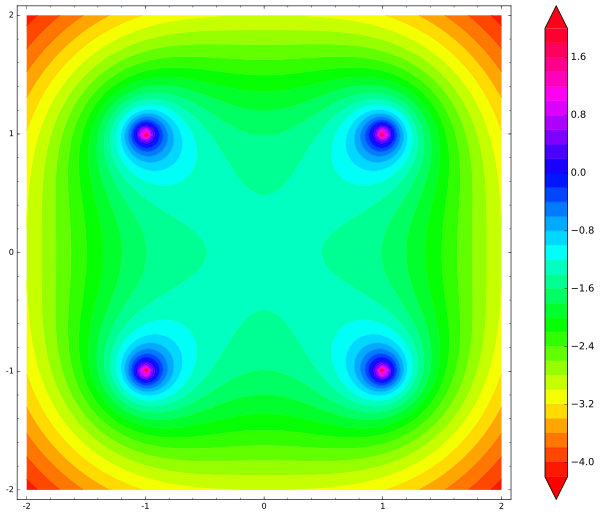
请注意，任何地方都没有本地最小值。 中心是鞍点或不稳定平衡点。 一旦免费电荷离开中心甚至一微米，它就会不可避免地飞出系统，并沿此方向加速，

等一下，您对方程式做了什么？

最初，当我意识到自己的计算完全违背Earnshaw定理时，我意识到自己在某个地方犯了错误。 从一开始就很容易跟踪我的步骤。 我深吸了一口气，继续阅读麦克斯韦方程组 。 再说一次，我在学校的表现不是很好：不是成绩（这些成绩很好），而是我从中学到的知识很多。 例如，我立即忘记了麦克斯韦方程，因为在大学及以后，我不需要与他们合作。

事实证明，它们非常简单，特别是如果我们仅在谈论静电定律！ 麦克斯韦方程有四个，每个定律对应一个：

• 高斯定律，我们稍后将需要它。 简而言之，这是一个守恒定律：不能一无所有地创造能量，也不能摧毁它。
• 磁场的高斯定律本质上是相同的。 而且我们还没有进入磁场，因为我们只是在谈论带电粒子。 跳过该法律。
• 法拉第定律：动磁铁产生电场。 很有意思，我们稍后再讨论。
• 安培定律：移动电场会产生磁场。 对我们的目的没用。

因此，这四个定律将电场和磁场两个矢量E和B绑定在一起。 这些向量是具有四个自变量（x，y，z，t）的函数，每四个自变量与一个三维向量并列。 我们对磁场不是很感兴趣，所以让我们看一下电场或E（x，y，z，t）。 别忘了我们处于静电领域，因此E在整个时间都是恒定的。 您可以将这个向量想象成一条河流，在每个点上我们都说出水流向何处以及流向何处。

法拉第定律指出，时间常数E场（我们在这里讲静电）没有任何卷曲 。

静电势如何与电场连接？ 简单：如果E字段是无卷曲的（如此处所示），那么我们可以用一种方法创建u（回到河流示例），该方法被1米高的水层覆盖（所有高度！ ）和“释放：它，水流的速度和方向将产生E场。 或者，用数学术语来说，可以找到一个标量u函数，其梯度等于E字段。

高斯定律指出：采取小邻里关系。 如果我们没有故意向其中收费，那么流入邻里的“水”的数量就等于流出的数量。 如果我们想听起来很聪明，则E域的差异为零。

请记住：E字段是标量函数u的导数。 如果其散度为零，则意味着u的拉普拉斯算子为零。 拉普拉斯算子是函数“曲率”的一个明智的词汇。 如果我们谈论的是单变量函数，那么拉普拉斯算子就是二阶导数。 在二变量函数中，拉普拉斯算子是两个导数之和。 如果等于零，则一个方向的曲率应被另一方向的曲率抵消。 意思是，薯片可以存在：



但是零拉普拉斯函数不具有局部最小值（或最大值），这意味着可以使用薯片，但不允许使用山峰：



想象一下将一圈（弯曲）的导线浸入肥皂水中。 然后，肥皂膜形成零拉普拉斯表面：



这就是所谓的“最小表面”。 肥皂膜要尽可能地小，因此逻辑上是，如果肥皂膜具有一定的局部最大值，则通过将其平滑将得到较小的膜，因此没有任何膜。 因此，静电势是一种最小的表面，没有局部最大值（只要我们没有故意在此处放置电荷）。

1 / r函数在三个维度上都具有零拉普拉斯算子，但在二维中却没有！ 如果要绘制二维示例，则需要解决Dirichlet问题 -对于2D，它是-ln r。

在1维或2维空间中使用平方反比公式相当于以其他方式限制电荷沿着其余轴的移动。 在这种情况下，很明显可以进行稳定的配置-只需拿一个纸板管，垂直放置并放下磁铁即可。 然后可以在其中放置另一个磁体，该磁体将处于平衡状态-在水平方向上，它受管的约束（即，处于一维空间中），并且重力的垂直方向和磁体的斥力得到平衡。 恩肖定理要么需要应用平方反比定律，要么以3d形式应用，或者在任意维度的空间中但具有相应的电势。 “对应的”是指从麦克斯韦方程式获得的那个。

恩萧定理及其后果

因此，回到带有一个自由带电粒子的示例。 静电场的电势没有局部最小值，因此，粒子的势能也没有局部最小值。 因此，一个粒子无法在静态场中达到稳定的平衡。 恭喜，我们已经证明了Earnshaw定理。 但是更复杂的系统呢？ 如何在那里应用定理？

根据我的老板的说法，这是另一个例子，它应该反驳Earnshaw定理。 让我们修复两个装药，并创建一个运动的物体，该装具由重量轻且不可拉伸的棒组成，两端带有装药：



凭直觉，如果我们将摇杆稍微向左或向右移动，那么两端之一将更靠近固定装药，这将推开它并将其返回到原始位置。 那么有什么收获呢？ 让我们绘制两个固定电荷的静电势图：

 var('x,y') def unit_potential(a,b,x,y): return -ln(sqrt((xa)^2 + (yb)^2)) def system_potential(x,y): return unit_potential(0,1,x,y)+unit_potential(0,-1,x,y) contour_plot(system_potential(x,y), (x, -2, 2), (y, -2, 2), cmap='hsv', contours=30, figsize=12, colorbar=True) 

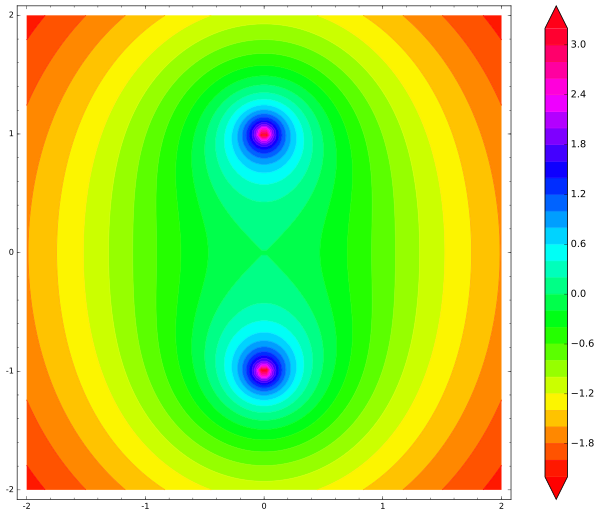
我们如何显示棍子的势能？ 摇杆具有三个自由度（两个用于移动，一个用于旋转），因此图形将是四维的。 现在让我们忽略旋转，只让摇杆左右移动。 我们将一根点固定在一根棒上（例如，棒的中心），并绘制棒的中心的势能图。 在这种情况下，棒的总势能是其两端电荷的势能之和：

 var('x,y') def unit_potential(a,b,x,y): return -ln(sqrt((xa)^2 + (yb)^2)) def system_potential(x,y): return unit_potential(0,1,x,y)+unit_potential(0,-1,x,y) def energy(x,y): return system_potential(x+2,y)+system_potential(x-2,y) contour_plot(energy(x,y), (x, -3, 3), (y, -2, 2), cmap='hsv', contours=30, figsize=12, colorbar=True) 

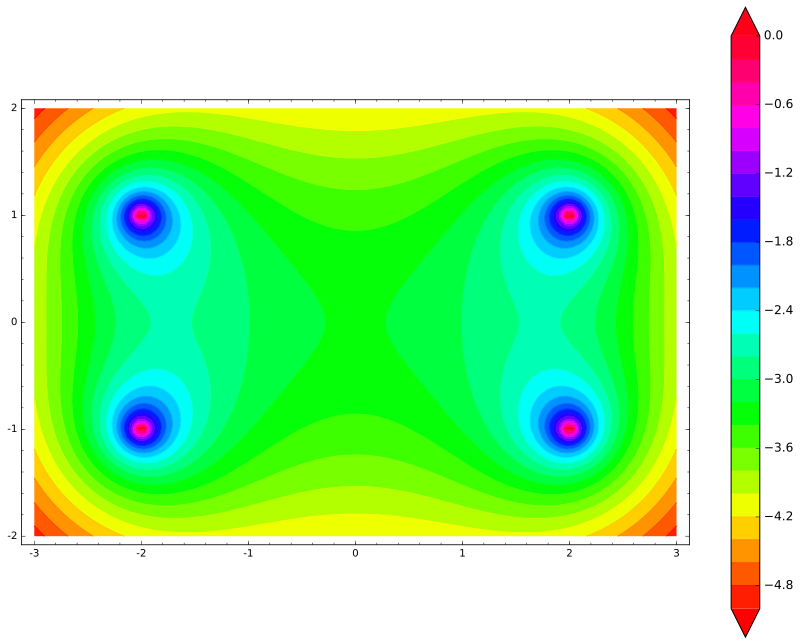
因此，棒的能量有四个峰值（每个末端可以击中两个电荷中的每个）。 正如预期的那样，操纵杆不会水平移动-而是会垂直移动！

这是合乎逻辑的，因为我们是如何获得能量的？ 我们将每次充电的势能加起来。 我们知道每个电荷的势能是零拉普拉斯函数。 因此，其总和也为零拉普拉斯算式。 因此，任何带电物体（不仅仅是我们的棍子！）的势能在静电场中都不能有最小值！

结论

在物理领域工作不紧密的人的磁场和电场的直观图像可能会产生误导。 我们的大脑通过使能量最小的图像来欺骗我们。 不幸的是，事实并非如此，如果没有机械支撑，制造出一个没有机械支撑的Mendocino电机是非常困难的。

有哪些漏洞可以利用？ 厄恩肖定理（如果我们将其应用于磁体）仅适用于固定的静态磁体系统 。

1. 我们可以创建一个动态磁场。
2. 反磁性和超导体也不属于Earnshaw定理。
3. 此处根本没有讨论移动（尤其是旋转）的物体，其中最著名的例子是莱维创 。

不，这并非没有希望。 当然，使用任何这些漏洞都会破坏Mendocino电机的美观性，但是自由悬浮的金属物体的魔力会胜过所有这些！

最后要注意的是：Earnshaw定理证明了固体物质的不存在，因此证明了原子的公认模型，从而导致了“行星”原子模型。