🌟 🕺🏾 👩🏾‍🎨 N个物体的任务或如何在不离开厨房的情况下炸毁星系 👨🏽‍✈️ 😃 🤹🏽

不久前，我读了刘奇新的科幻小说《三体问题》。在其中，一些外星人遇到了一个问题-他们不知道如何以足够的准确度来计算自己星球的轨迹。与我们不同，他们生活在三星级系统中，星球上的“天气”在很大程度上取决于它们的相对位置-从焚烧的热量到冰冷的天气。我决定检查我们是否可以解决此类问题。

现象的物理

要理解问题，有必要处理现象的物理现象。在古典理论的框架中，两个物体的吸引力由牛顿定律确定：

$\ vec {F}（\ vec {r} _1，\ vec {r} _2）=-G m_1 m_2 \ frac {\ vec {r} _1-\ vec {r} _2} {| \ vec {r} _1-\ vec {r} _2 | ^ 3}，$

在哪里

$\ vec {r} _1，\ vec {r} _2$ -物体在太空中的位置，

$m_1，m_2$ -大量的身体，

$G$ -重力常数。
在系统中

$N$ 每个身体上的身体都会受到其余身体的吸引力的影响，其方程式如下：

$\ vec {F} _n = -G \ sum_ {k \ neq n} m_n m_k \ frac {\ vec {r} _n-\ vec {r} _k} {| \ vec {r} _n-\ vec {r } _k | ^ 3}。$

使用牛顿第二定律，我们为每个粒子写加速度：

$\ vec {a} _n = \ vec {F} _n / m_n = -G \ sum_ {k \ neq n} m_k \ frac {\ vec {r} _n-\ vec {r} _k} {| \ vec { r} _n-\ vec {r} _k | ^ 3}。$

回顾加速度是坐标的第二时间导数，我们获得了一个二阶偏微分方程，必须求解该方程才能获得每个物体的轨迹：

$\ frac {\部分^ 2 \ vec {r} _n} {\部分t ^ 2} = f_n = -G \ sum_ {k \ neq n} m_k \ frac {\ vec {r} _n-\ vec {r } _k} {| \ vec {r} _n-\ vec {r} _k | ^ 3}。$

这里要注意的是，计算函数的复杂性

$f_n$ 等于

$O（N ^ 2）$ 并且随着相互作用体数量的增加而显着增加。

数学

求解微分方程的第一个也是最简单的方法是Euler方法，该方法设计用于求解以下形式的方程：

$\ frac {dy} {dx} = f（x，y）。$

过渡到离散区域后，我们获得：

$y_ {i} = y_ {i-1} + h f（x_ {i-1}，y_ {i-1}），\ quad i = 1,2,3，\点，m，$

在哪里

$h$ 是整合步骤，并且

$m$ -集成步骤数。因此，如果我们需要一次计算物体的位置

$T$ 那我们应该做

$m =吨/小时$ 整合步骤。在这里第一个问题是可见的-如果

$T$ 很大，那么我们需要采取大量的集成步骤。

要将欧拉方法应用于我们的问题，应将其简化为一阶系统。为此，我们引入了另一个变量-粒子速度：

$\ frac {\部分\ vec {v} _n} {\部分t} = f_n，\\ \ frac {\部分\ vec {r} _n} {\部分t} = \ vec {v} _n。$

解微分方程组的第二个问题是解及其控制的准确性。可以通过两种方式提高准确性：通过减少积分步骤和选择具有更高准确性的方法。两种方法都导致计算复杂性的增加，但是方式不同。例如，您可以使用经典的四阶Runge-Kutta方法；它需要四个函数计算

$f_n$ 在每个步骤中，但具有一定的准确性

$O（h ^ 4）$ （为了进行比较，欧拉方法的精度为

$O（h）$ 并需要进行一次计算

$f_n$ ）解决方案的准确性也可以通过多种方式控制：与分析解决方案进行比较，使用不同方法或不同步骤进行解决并比较结果，控制解决方案必须遵守的第三方参数和限制。
而且，这些方法中的每一种都有其缺点。可能没有分析决定，或者甚至在大多数情况下，甚至是完全没有。例如，对于我们的任务

$N$ 电话分析解决方案仅适用于

$N = 2$ ，但这足以测试方法的准确性。用两种方法或用不同的步骤解决问题会增加计算时间，但是这种方法几乎可以应用于任何任务。并非每项任务都有局限性，但对我们而言，它们都有局限性：在整合的每个步骤中，我们都可以控制保护法的执行。这种方法也增加了计算的复杂性，但是有很多选择，所有粒子的动量和或角动量之和的计算都非常复杂。

$O（N）$ ，而计算系统的总能量具有阶数复杂性

$O（N ^ 2）$

关于计算总能量的注意事项

在我们的案例中，系统的总能量由两部分组成-动能和势能。动能由所有物体的动能之和组成。要计算势能，我们需要在剩余粒子的引力场中将每个粒子的势能相加，因此我们需要添加

$O（N ^ 2）$ 条款。困难在于所有项的阶次非常不同，即使使用双精度计算，也无法以足以在不同步骤进行比较的精度来计算该值。为了克服这个问题，有必要根据Kahan算法进行求和。

图1. 椭圆轨迹的示例。

考虑一下卫星绕地球椭圆轨道运动的简单情况。随着卫星接近地球，其速度会增加，而当远离地球移动时，其速度会降低，因此有可能减少轨道绿色部分的时间积分步长，并以红色和蓝色增加积分步长而不会改变解决方案的精度。让我们尝试更详细地比较。

表1. 研究微分方程的研究方法

已标记	订购	内容描述
亚当斯	1-5	亚当斯-巴什福特法
欧拉	1个	欧拉法
rk4	4	经典Runge-Kutta方法
尔克	5	卡什卡普方法
rkdp	5	多曼王子法
rkdverk	6	Werner方法1） p。 181
rkf	7	费尔伯格方法1） p。 180
kg	6	隐含高斯-勒格德方法
rklc	4	隐式Lobatto方法
空中飞人	2	梯形法

要为我们的任务选择最佳方法，我们将比较几种已知方法。为此，我们模拟了两个物体系统的碰撞

$N = 512$ 并在仿真结束时测量总能量，动量及其矩的相对变化（最大仿真时间

$T_ {max} = 2.5$ ）在这种情况下，我们将更改集成方法的步骤和参数，并测量函数调用的次数

$f_n$ 分别地，那些具有较少调用次数的方法将导致较少的损失，我们将认为更可接受。


a）	b）
图2. 系统仿真结束时能量的相对变化a），动量b） $N = 512$ 根据函数计算的数量，通过各种方法选择主体 $f_n$ 双精度

从图2的图表可以看出，函数计算量的最佳比率

$f_n$ 以及五阶Adams和Dorman-Prince方法中物体系统能量的相对变化。还可以看到，对于所有方法，计算量都会增加

$f_n$ 系统动量的相对变化增加。对于能量的相对变化，这也很明显，但仅适用于可能达到阈值的几种方法

$dE / E_0 <10 ^ {-12}$ 。这种影响不能再归因于方法的错误，而应归因于计算的错误，并且只有随着浮点数计算精度的提高，精度的进一步提高才可能实现。


a）	b）
图3. 系统仿真结束时，能量a），动量b）的相对变化 $N = 512$ 根据函数计算的数量，通过各种方法选择主体 $f_n$ 具有四倍精度（__float128）

图3a和3b表明，使用具有四倍精度的计算可以将相对能量损失降低至

$10 ^ {-23}$ ，但您需要了解，与双精度相比，计算时间增加了两个数量级。与双精度计算一样，最佳精度比率和函数计算次数

$f_n$ 拥有五阶亚当斯和多曼王子的方法。

Dorman-Prince和Werner 方法属于嵌套方法类，可以同时计算两个精度高低的解决方案（对于Dorman-Prince方法，精度为5和4，对于Werner方法，精度为6和5）。如果这两种解决方案非常不同，那么我们可以将当前的集成步骤分解为更小的解决方案。这使我们能够动态更改集成步骤，并仅在需要的地方减少集成步骤。

让我们在更长的系统仿真间隔内更详细地比较五阶Dorman-Prince，Werner和Adams方法（

$T_ {max} = 300$ ）

a） 建模过程中能量，动量及其动量 的 相对变化

b） 函数计算次数

$f_n$ 在模拟间隔

$\ Delta T = 0.3$

图4. 系统物理参数的相对变化与功能计算次数的关系

$f_n$ 使用Dorman-Prince可变步长法不时建模

$h = 10 ^ {-5} \点10 ^ {-9}$

a） 建模过程中能量，动量及其动量 的 相对变化

b） 函数计算次数

$f_n$ 在模拟间隔

$\ Delta T = 0.3$

图5. 系统物理参数的相对变化和功能计算次数的依赖性

$f_n$ 可变步长的Werner方法进行时间建模

$h = 10 ^ {-5} \点10 ^ {-9}$

图6. 用五阶Adams-Bashfort方法建模时，能量，动量及其矩的相对变化

$h = 10 ^ {-6}$

图7. 函数计算数量的依存关系

$f_n$ 从仿真时间开始用于五阶Adams，Dorman-Prince和Werner方法

可以看出，在我们系统发展的初期（

$T <25$ ）这三种方法都显示出相似的特性，但是在后期系统中会发生某些事件，其结果是系统主要参数（总能量，动量及其动量）的误差急剧上升。但是由于减少了“复杂”部分中的积分步骤的能力，Dorman-Prince和Werner方法能够更好地应对这些变化，结果是函数计算的数量增加了

$f_n$ 如图4b和5b所示，但计算总数

$f_n$ 嵌套方法比Adams-Bashfort方法要小，如图7所示。

我不知道这些时候系统发生了什么

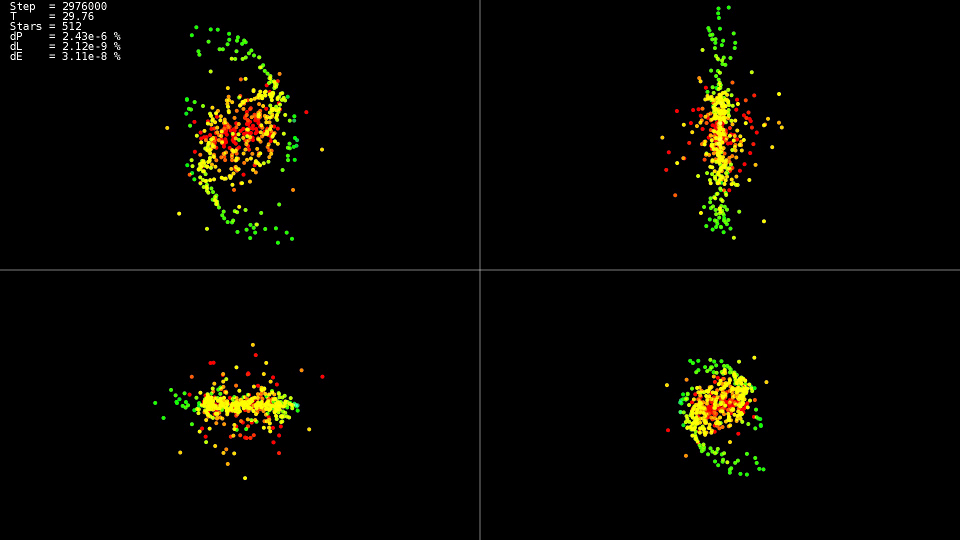
视频1. 建模512个实体的系统。 Dorman-Prince方法。 动态步进

$h = 10 ^ {-5} \点10 ^ {-9}$

视频演示了这一点

$T = 25$ 运动相对平静，此后“星系”中心发生碰撞，这导致轨迹的急剧变化和某些粒子的速度大大增加。此外，为了保持解决方案的准确性，有必要减少集成步骤。嵌套方法可以自动执行此操作；图表显示，在系统演化的某些部分中，集成步骤减少了近两个数量级

$10 ^ {-5}$ 之前

$h = 10 ^ {-7}$ 。当使用Adams方法以及在整个系统演化过程中采取这样的步骤时，我们就不必等待解决方案了。

总结

对于该解决方案，最好使用嵌套方法，这些方法允许您动态控制积分步骤，并仅在轨迹的“复杂”部分上减少积分步骤。

不要追逐最高顺序的方法。即使使用“双精度”数据类型，它们也无法发挥其潜在功能，但以更高的精度使用相同的数据类型会极大地增加解决问题所需的时间。

CPU实施

现在定义了求解方程的方法的选择，让我们尝试计算每个粒子的相互作用力的计算。对于所有粒子，我们得到一个双循环：

实现代码“简单”

for(size_t body1 = 0; body1 < count; ++body1) { const nbvertex_t v1(rx[ body1 ], ry[ body1 ], rz[ body1 ]); nbvertex_t total_force; for(size_t body2 = 0; body2 != count; ++body2) { if(body1 == body2) { continue; } const nbvertex_t v2(rx[ body2 ], ry[ body2 ], rz[ body2 ]); const nbvertex_t force(m_data->force(v1, v2, mass[body1], mass[body2])); total_force += force; } frx[body1] = vx[body1]; fry[body1] = vy[body1]; frz[body1] = vz[body1]; fvx[body1] = total_force.x / mass[body1]; fvy[body1] = total_force.y / mass[body1]; fvz[body1] = total_force.z / mass[body1]; }

每个物体的重力是独立计算的，要使用所有处理器核心，在第一个循环之前编写OpenMP指令就足够了：

一段来自“ openmp”实现的代码

 #pragma omp parallel for for(size_t body1 = 0; body1 < count; ++body1)

因为每个主体彼此交互，然后减少处理器与RAM的交互次数并提高缓存使用率，我们可以将部分数据加载到缓存中并重复使用：

实现代码“ openmp +块”

 #pragma omp parallel for for(size_t n1 = 0; n1 < count; n1 += BLOCK_SIZE) { nbcoord_t x1[BLOCK_SIZE]; nbcoord_t y1[BLOCK_SIZE]; nbcoord_t z1[BLOCK_SIZE]; nbcoord_t m1[BLOCK_SIZE]; nbvertex_t total_force[BLOCK_SIZE]; for(size_t b1 = 0; b1 != BLOCK_SIZE; ++b1) { size_t local_n1 = b1 + n1; x1[b1] = rx[local_n1]; y1[b1] = ry[local_n1]; z1[b1] = rz[local_n1]; m1[b1] = mass[local_n1]; } for(size_t n2 = 0; n2 < count; n2 += BLOCK_SIZE) { nbcoord_t x2[BLOCK_SIZE]; nbcoord_t y2[BLOCK_SIZE]; nbcoord_t z2[BLOCK_SIZE]; nbcoord_t m2[BLOCK_SIZE]; for(size_t b2 = 0; b2 != BLOCK_SIZE; ++b2) { size_t local_n2 = b2 + n2; x2[b2] = rx[local_n2]; y2[b2] = ry[local_n2]; z2[b2] = rz[local_n2]; m2[b2] = mass[n2 + b2]; } for(size_t b1 = 0; b1 != BLOCK_SIZE; ++b1) { const nbvertex_t v1(x1[ b1 ], y1[ b1 ], z1[ b1 ]); for(size_t b2 = 0; b2 != BLOCK_SIZE; ++b2) { const nbvertex_t v2(x2[ b2 ], y2[ b2 ], z2[ b2 ]); const nbvertex_t force(m_data->force(v1, v2, m1[b1], m2[b2])); total_force[b1] += force; } } } for(size_t b1 = 0; b1 != BLOCK_SIZE; ++b1) { size_t local_n1 = b1 + n1; frx[local_n1] = vx[local_n1]; fry[local_n1] = vy[local_n1]; frz[local_n1] = vz[local_n1]; fvx[local_n1] = total_force[b1].x / m1[b1]; fvy[local_n1] = total_force[b1].y / m1[b1]; fvz[local_n1] = total_force[b1].z / m1[b1]; } }

进一步的优化包括取出计算主循环力的功能内容，并消除体重m1 [b1]的除法和乘法。除了我们稍微减少了计算量这一事实外，编译器将能够在如此扩展的周期上应用SSE和AVX处理器的矢量指令。

实现代码“ openmp +块+优化”

 #pragma omp parallel for for(size_t n1 = 0; n1 < count; n1 += BLOCK_SIZE) { nbcoord_t x1[BLOCK_SIZE]; nbcoord_t y1[BLOCK_SIZE]; nbcoord_t z1[BLOCK_SIZE]; nbcoord_t total_force_x[BLOCK_SIZE]; nbcoord_t total_force_y[BLOCK_SIZE]; nbcoord_t total_force_z[BLOCK_SIZE]; for(size_t b1 = 0; b1 != BLOCK_SIZE; ++b1) { size_t local_n1 = b1 + n1; x1[b1] = rx[local_n1]; y1[b1] = ry[local_n1]; z1[b1] = rz[local_n1]; total_force_x[b1] = 0; total_force_y[b1] = 0; total_force_z[b1] = 0; } for(size_t n2 = 0; n2 < count; n2 += BLOCK_SIZE) { nbcoord_t x2[BLOCK_SIZE]; nbcoord_t y2[BLOCK_SIZE]; nbcoord_t z2[BLOCK_SIZE]; nbcoord_t m2[BLOCK_SIZE]; for(size_t b2 = 0; b2 != BLOCK_SIZE; ++b2) { size_t local_n2 = b2 + n2; x2[b2] = rx[local_n2]; y2[b2] = ry[local_n2]; z2[b2] = rz[local_n2]; m2[b2] = mass[n2 + b2]; } for(size_t b1 = 0; b1 != BLOCK_SIZE; ++b1) { for(size_t b2 = 0; b2 != BLOCK_SIZE; ++b2) { nbcoord_t dx = x1[b1] - x2[b2]; nbcoord_t dy = y1[b1] - y2[b2]; nbcoord_t dz = z1[b1] - z2[b2]; nbcoord_t r2(dx * dx + dy * dy + dz * dz); if(r2 < NBODY_MIN_R) { r2 = NBODY_MIN_R; } nbcoord_t r = sqrt(r2); nbcoord_t coeff = (m2[b2]) / (r * r2); dx *= coeff; dy *= coeff; dz *= coeff; total_force_x[b1] -= dx; total_force_y[b1] -= dy; total_force_z[b1] -= dz; } } } for(size_t b1 = 0; b1 != BLOCK_SIZE; ++b1) { size_t local_n1 = b1 + n1; frx[local_n1] = vx[local_n1]; fry[local_n1] = vy[local_n1]; frz[local_n1] = vz[local_n1]; fvx[local_n1] = total_force_x[b1]; fvy[local_n1] = total_force_y[b1]; fvz[local_n1] = total_force_z[b1]; } }

表2. 函数计算时间的依赖性（以秒为单位）

$f_n$ 相互作用体的数量

$N$ 用于各种CPU实现

$N$	2048	4096	8192	16384	32768
简单的	0.0425	0.1651	0.6594	2.65	10.52
的openmp	0.0078	0.0260	0.1079	0.417	1.655
openmp +块+优化	0.0037	0.0128	0.0495	0.194	0.774

系统参数：

系统： Debian 9，Intel Core i7-5820K（6核心）
编译器： gcc 6.3.0

可以清楚地看到，具有OpenMP支持的版本在内核数量方面的速度提高了六倍，而优化版本的速度甚至快了两倍多。因此，通过优化，您不应该仅依赖于并发。有趣的是，在单流计算中，处理器的工作频率为3.6 GHz，在并行版本（openmp）中，该频率降至3.4 GHz，而在并行优化中（openmp + block +最优化），该频率降至3.3 GHz，但这这并没有阻止她更快地工作13.6倍。还可以看到，随着问题大小的增加，计算时间的增加是二次方的，并且进一步增加

$N$ 使任务在合理的时间内无法解决。

GPU实施

但是，人们希望更快地进行计算。有几种方向可用于加速：GPU计算，函数逼近

$f_n$ 。首先，对于GPU计算，我选择了OpenCL技术。为了更方便的工作，使用了CLHPP库。 OpenCL的主要优点是代码可以在处理器和GPU上运行，从而简化了编写和调试，并扩展了要运行的硬件列表。 Oclgrind工具有助于调试，该调试在运行时显示不正确的OpenCL API调用和内存访问问题。

Opencl的

要开始使用OpenCL，您需要获取可用平台的列表。最常见的平台是AMD，Intel和NVidia。

代号

 std::vector<cl::Platform> platforms; cl::Platform::get(&platforms);

接下来，在选择平台之后，您需要选择该平台代表的计算设备：

代号

 const cl::Platform& platform(platforms[platform_n]); std::vector<cl::Device> all_devices; platform.getDevices(CL_DEVICE_TYPE_ALL, &all_devices);

在准备阶段的最后，有必要创建一个上下文和队列，以在其中分配内存并执行计算。例如，创建一个将选定平台的所有计算设备组合在一起的上下文，如下所示：

上下文和队列创建代码

 cl::Context context(all_devices); std::vector<cl::CommandQueue> queues; for(cl::Device device: all_devices) queues.push_back(cl::CommandQueue(context, device));

要将源代码下载到计算设备，必须将其编译，cl :: Program类用于此目的。

内核编译代码

 std::vector< std::string > source_data; cl::Program::Sources sources; for(int i = 0; i != files.size(); ++i) { source_data.push_back(load_program(files[i]));//   sources.push_back(std::make_pair(source_data.back().data(), source_data.back().size())); } cl::Program prog(context, sources); devices.push_back(all_devices); prog.build(devices, options);

为了描述在计算设备上执行的功能（内核）的参数，有一个cl模板：make_kernel。

交互强度计算内核示例

 typedef cl::make_kernel< cl_int, cl_int, //Block offset cl::Buffer, //mass cl::Buffer, //y cl::Buffer, //f cl_int, cl_int, //yoff,foff cl_int, cl_int //points_count,stride > ComputeBlock;

此外，一切都很简单：我们声明一个具有内核类型的变量，将编译后的程序和计算内核的名称传递给它，我们几乎可以像正常函数一样启动内核。

内核启动代码

 ComputeBlock fcompute(prog, "ComputeBlockLocal"); cl::NDRange global_range(device_data_size); cl::NDRange local_range(block_size); cl::EnqueueArgs eargs(ctx.m_queue, global_range, local_range); fcompute(eargs, ...  ); //,   .

OpenCL本身的计算核心与CPU的'openmp + block +最优化'选项非常相似，仅与CPU版本不同，第一个周期是使用OpenCL来控制的（周期范围由内核启动代码中的global_range变量确定，而当前的迭代编号可从内核获取）使用函数get_global_id（0））。首先，部分身体数据从本地内存加载，然后进行处理。本地内存是该组中所有线程所共有的，因此该下载对于该组仅发生一次，并由该组中的每个线程进行处理，并且本地内存比全局内存要快得多，计算要快得多。

内核代码

 __kernel void ComputeBlockLocal(int offset_n1, int offset_n2, __global const nbcoord_t* mass, __global const nbcoord_t* y, __global nbcoord_t* f, int yoff, int foff, int points_count, int stride) { int n1 = get_global_id(0) + offset_n1; __global const nbcoord_t* rx = y + yoff; __global const nbcoord_t* ry = rx + stride; __global const nbcoord_t* rz = rx + 2 * stride; __global const nbcoord_t* vx = rx + 3 * stride; __global const nbcoord_t* vy = rx + 4 * stride; __global const nbcoord_t* vz = rx + 5 * stride; __global nbcoord_t* frx = f + foff; __global nbcoord_t* fry = frx + stride; __global nbcoord_t* frz = frx + 2 * stride; __global nbcoord_t* fvx = frx + 3 * stride; __global nbcoord_t* fvy = frx + 4 * stride; __global nbcoord_t* fvz = frx + 5 * stride; nbcoord_t x1 = rx[n1]; nbcoord_t y1 = ry[n1]; nbcoord_t z1 = rz[n1]; nbcoord_t res_x = 0.0; nbcoord_t res_y = 0.0; nbcoord_t res_z = 0.0; __local nbcoord_t x2[NBODY_DATA_BLOCK_SIZE]; __local nbcoord_t y2[NBODY_DATA_BLOCK_SIZE]; __local nbcoord_t z2[NBODY_DATA_BLOCK_SIZE]; __local nbcoord_t m2[NBODY_DATA_BLOCK_SIZE]; // NB! get_local_size(0) == NBODY_DATA_BLOCK_SIZE for(int b2 = 0; b2 < points_count; b2 += NBODY_DATA_BLOCK_SIZE) { int n2 = b2 + offset_n2 + get_local_id(0); // Copy data block to local memory x2[ get_local_id(0) ] = rx[n2]; y2[ get_local_id(0) ] = ry[n2]; z2[ get_local_id(0) ] = rz[n2]; m2[ get_local_id(0) ] = mass[n2]; // Synchronize local work-items copy operations barrier(CLK_LOCAL_MEM_FENCE); nbcoord_t local_res_x = 0.0; nbcoord_t local_res_y = 0.0; nbcoord_t local_res_z = 0.0; for(int local_n2 = 0; local_n2 != NBODY_DATA_BLOCK_SIZE; ++local_n2) { nbcoord_t dx = x1 - x2[local_n2]; nbcoord_t dy = y1 - y2[local_n2]; nbcoord_t dz = z1 - z2[local_n2]; nbcoord_t r2 = (dx * dx + dy * dy + dz * dz); if(r2 < NBODY_MIN_R) { r2 = NBODY_MIN_R; } nbcoord_t r = sqrt(r2); nbcoord_t coeff = (m2[local_n2]) / (r * r2); dx *= coeff; dy *= coeff; dz *= coeff; local_res_x -= dx; local_res_y -= dy; local_res_z -= dz; } // Synchronize local work-items computations barrier(CLK_LOCAL_MEM_FENCE); res_x += local_res_x; res_y += local_res_y; res_z += local_res_z; } frx[n1] = vx[n1]; fry[n1] = vy[n1]; frz[n1] = vz[n1]; fvx[n1] = res_x; fvy[n1] = res_y; fvz[n1] = res_z; }

库达

NVidia CUDA平台的实现比OpenCL更为简单，我们不需要创建设备上下文并自行管理执行队列（至少在我们要进行多GPU实现之前）。与OpenCL一样，我们需要在GPU上分配内存，将数据复制到其中，然后才能启动计算核心。

您可以在此处阅读有关使用CUDA的更多信息。

CUDA内核启动代码

 dim3 grid(count / block_size); dim3 block(block_size); size_t shared_size(4 * sizeof(nbcoord_t) * block_size); kfcompute <<< grid, block, shared_size >>> (... ...);

与OpenCL不同，CUDA并未指定完整的迭代范围（在OpenCL实现中为global_range），而是在网格中设置了网格大小和块大小，因此，当前主体数的计算会略有变化，否则内核与OpenCL非常相似，除了其他名称之外共享内存的同步和说明符功能。 CUDA的另一个有用的区别功能是，我们可以在内核启动时指定所需的共享内存大小。与OpenCL实施一样，在每个迭代块的开头，我们将部分数据复制到共享内存中，然后从该块的所有线程中使用该内存。

CUDA内核代码

 __global__ void kfcompute(int offset_n2, const nbcoord_t* y, int yoff, nbcoord_t* f, int foff, const nbcoord_t* mass, int points_count, int stride) { int n1 = blockDim.x * blockIdx.x + threadIdx.x; const nbcoord_t* rx = y + yoff; const nbcoord_t* ry = rx + stride; const nbcoord_t* rz = rx + 2 * stride; nbcoord_t x1 = rx[n1]; nbcoord_t y1 = ry[n1]; nbcoord_t z1 = rz[n1]; nbcoord_t res_x = 0.0; nbcoord_t res_y = 0.0; nbcoord_t res_z = 0.0; extern __shared__ nbcoord_t shared_xyzm_buf[]; nbcoord_t* x2 = shared_xyzm_buf; nbcoord_t* y2 = x2 + blockDim.x; nbcoord_t* z2 = y2 + blockDim.x; nbcoord_t* m2 = z2 + blockDim.x; for(int b2 = 0; b2 < points_count; b2 += blockDim.x) { int n2 = b2 + offset_n2 + threadIdx.x; // Copy data block to local memory x2[ threadIdx.x ] = rx[n2]; y2[ threadIdx.x ] = ry[n2]; z2[ threadIdx.x ] = rz[n2]; m2[ threadIdx.x ] = mass[n2]; // Synchronize local work-items copy operations __syncthreads(); nbcoord_t local_res_x = 0.0; nbcoord_t local_res_y = 0.0; nbcoord_t local_res_z = 0.0; for(int n2 = 0; n2 != blockDim.x; ++n2) { nbcoord_t dx = x1 - x2[n2]; nbcoord_t dy = y1 - y2[n2]; nbcoord_t dz = z1 - z2[n2]; nbcoord_t r2 = (dx * dx + dy * dy + dz * dz); if(r2 < NBODY_MIN_R) { r2 = NBODY_MIN_R; } nbcoord_t r = sqrt(r2); nbcoord_t coeff = (m2[n2]) / (r * r2); dx *= coeff; dy *= coeff; dz *= coeff; local_res_x -= dx; local_res_y -= dy; local_res_z -= dz; } // Synchronize local work-items computations __syncthreads(); res_x += local_res_x; res_y += local_res_y; res_z += local_res_z; } n1 += foff; f[n1 + 3 * stride] = res_x; f[n1 + 4 * stride] = res_y; f[n1 + 5 * stride] = res_z; }

表3. 计算时间（以秒为单位）函数的依赖性

$f_n$ 相互作用体的数量

$N$ 适用于各种GPU实现和更好的CPU实现

$N$	4096	8192	16384	32768	65536	131072
openmp +块+优化	0.0128	0.0495	0.194	0.774	---	---
OpenCL +一半NVidia K80	0.004	0.008	0.026	0.134	0.322	1.18
CUDA +一半NVidia K80	0.004	0.008	0.0245	0.115	0.291	1.13

哪里可以买到NVidia K80

Google的免费Colab服务启动了OpenCL和CUDA实施，该服务提供对NVidia K80计算机的访问。您可以在集线器上阅读有关使用此服务的更多信息。

通常，结果令人失望，仅比CPU实现快5-6倍。即使我们对整个K80进行计算，我们也会获得高达12倍的加速度，但是由于任务的复杂性是二次的，因此在合理的时间内，我们将不能处理32768个交互体，而可以处理131072，仅多了4倍。

函数近似 $f_n$

如果仔细看一下由两个物体的吸引力设置的函数，很明显它随距离呈二次方减小。因此，我们可以准确地计算出近身之间以及近身之间的相互作用力。一种著名的方法
是D.Barnes和P.Hat提出的树码算法。在模拟空间中构造了八叉树，其叶子中包含模拟物体的坐标和质量。父节点包含质心，子节点的总质量以及围绕子节点的实体描述的球体的半径。树的根包含所有物体的质心，它们的总质量以及围绕它们描述的球体的半径。在计算相互作用力时，如果到节点的距离与其半径之比大于某个常数，则首先要考虑到树根的距离

$\ lambda_ {crit}$ ，则该根被认为是一个坐标等于其所包含的物体的质心坐标的物体，并且如果该比率小于或等于，则其质量等于子节点的质量之和。

$\ lambda_ {crit}$ ，然后为每个子节点递归地重复该过程。如果到达树的叶子，则以通常的方式考虑相互作用力。因此，如果一个物体远离其他物体的紧凑组，则将该组作为一个物体呈现给它，并且不计算每个物体的相互作用力，而只计算一个物体。因此，算法的复杂度随着

$O（N ^ 2）$ 之前

$O（N \日志（N））$ 以牺牲一些准确性为代价。

在我的方法中，我决定不使用octree 树，而是使用kd树，因为与八叉树相比，它更易于使用并且具有较低的存储开销。

让我们回到在CPU上的实现。 kd-tree节点可以以类的形式表示，该类包含指向左右后代的指针以及有关坐标和质量的信息：

Kd树节点

 class node { node* m_left; //!<   node* m_right; //!<   nbvertex_t m_mass_center; //!<     nbcoord_t m_mass; //!<   nbcoord_t m_radius_sqr; //!<    ,   lambda_crit nbvertex_t m_bmin; //!<     nbvertex_t m_bmax; //!<     size_t m_body_n; //!<  ,    };

使用这种存储树的方法，我们有两种可能的遍历树的选项：使用显式递归或自己使用堆栈。我选择了第二个选项。

通过遍历树计算相互作用力

 nbvertex_t force_compute(const nbvertex_t& v1, const nbcoord_t mass1) { nbvertex_t total_force; node* stack_data[MAX_STACK_SIZE] = {}; node** stack = stack_data; node** stack_head = stack; *stack++ = m_root; while(stack != stack_head) { node* curr = *--stack; const nbcoord_t distance_sqr((v1 - curr->m_mass_center).norm()); if(distance_sqr > curr->m_radius_sqr) {//  ,       total_force += force(v1, curr->m_mass_center, mass1, curr->m_mass); } else {//   ,      if(curr->m_right != NULL) { *stack++ = curr->m_right; } if(curr->m_left != NULL) { *stack++ = curr->m_left; } } } return total_force; }

与“精确” CPU实现的情况一样，每个主体都需要调用力计算功能。使用OpenMP指令可以轻松地并行化所有主体之间的循环。

但是在这种情况下，相邻循环迭代将引用树的完全不同的部分，这不允许有效使用处理器缓存。为了克服这个问题，所有物体都不必以原始顺序遍历，而是以物体位于kd-tree的叶子中的顺序遍历，然后对空间紧密的物体进行相邻的迭代，并将沿几乎相同的路径遍历树。

树叶遍历

 template<class Visitor> void traverse(Visitor visit) { node* stack_data[MAX_STACK_SIZE] = {}; node** stack = stack_data; node** stack_head = stack; *stack++ = m_root; while(stack != stack_head) { node* curr = *--stack; if(curr->m_radius_sqr > 0) {//  .    . if(curr->m_left != NULL) { *stack++ = curr->m_left; } if(curr->m_right != NULL) { *stack++ = curr->m_right; } } else {//   .  . visit(curr->m_body_n, curr->m_mass_center, curr->m_mass); } } }

此实现还有另一个问题-没有通用的方法可以并行化这种树遍历。但是，我们可以完全改变树在内存中的存储方式-我们可以将所有节点存储在一个线性数组中，并通过类似于二进制堆的构造完全放弃对后代的指针的存储。用以下命令开始编号节点时

$1$ 如果节点在单元格编号中

$我$ ，那么他的左孩子在牢房中

$2i$ ，单元格中的对子

$2i + 1$ ，以及单元格中的父级

$我/ 2$ 。右边的节点与左边对应的数字

$我$ 将有一个数字

$我+ 1$ 。数组本身将有一个长度

$2N$ ，并且所有叶节点将位于最后一个

$N$ 此外，单元间距很近的节点将位于阵列的紧密单元中。树遍历函数将有所变化，但是框架保持不变：

通过遍历数组中的树来计算力

 nbvertex_t force_compute(const nbvertex_t& v1, const nbcoord_t mass1) { nbvertex_t total_force; size_t stack_data[MAX_STACK_SIZE] = {}; size_t* stack = stack_data; size_t* stack_head = stack; *stack++ = NBODY_HEAP_ROOT_INDEX; while(stack != stack_head) { size_t curr = *--stack; const nbcoord_t distance_sqr((v1 - m_mass_center[curr]).norm()); if(distance_sqr > m_radius_sqr[curr]) { total_force += force(v1, m_mass_center[curr], mass1, m_mass[curr]); } else { size_t left(left_idx(curr)); size_t rght(rght_idx(curr)); if(rght < m_body_n.size()) { *stack++ = rght; } if(left < m_body_n.size()) { *stack++ = left; } } } return total_force; }

但这并不是将节点存储在数组中的所有可能，我们可以在爬网时拒绝堆栈。为此，在转到该节点的子节点的代码分支中，添加该函数以计算下一个节点（

$next_ {up}$ ），并在计算相互作用力的分支中，添加跳过当前子树的下一个节点的计算（

$skip_ {down}$ ）

要跳过当前子树，我们需要向下到根（方向

$D$ ），当我们在右后代中时，一到达左后，便转到相应的右子树（方向

$R$ ），如果我们到达根，那么树遍历就完成了。

子树跳过功能代码

 index_t skip_down(index_t idx) { // While index is 'right' -> go down while(is_right(idx)) { index_t parent = parent_idx(idx); // We at root again. Stop traverse. if(parent == NBODY_HEAP_ROOT_INDEX) { return NBODY_HEAP_ROOT_INDEX; } idx = parent; } return left2right(idx); }

图8. 跳过子树

$skip_ {down}$ 。

要转到下一个节点，请尽可能转到左子节点（方向

$inline$ ），如果没有后代，则使用函数“从下面”转到下一个节点

$skip_ {down}$ 。

转到下一个节点功能代码

 index_t next_up(index_t idx, index_t tree_size) { index_t left = left_idx(idx); if(left < tree_size) { return left; } return skip_down(idx); }

图9. 过渡到下一个节点

$next_ {up}$ 。

似乎我们用循环替换了递归

$而$ 在功能上

$skip_ {down}$ ，这样的替换不会给出任何结果，但是让我们看看如何确定一个节点是否带有数字

$我$ 右后裔。只需检查其奇数即可完成操作（正确的孩子在单元格中

$2i + 1$ ），因此足以计算

$我\＆1$ 。即我们将数字相除

$我$ 如果最低有效位设置为1，则为2。但这无需循环即可完成，在许多处理器中，都有一条查找第一设置指令返回第一设置位的位置，使用它我们将循环变成四个处理器指令。

优化的跳过子树功能代码

 index_t skip_down(index_t idx) { idx = idx >> (__builtin_ffs(~idx) - 1); return left2right(idx); }

之后，我们可以从树遍历函数中排除堆栈，并用一对替换

$skip_ {down} + next_ {up}$ ，之后函数看起来更简单：

通过遍历数组中的树而不使用堆栈来计算力

 nbvertex_t force_compute(const nbvertex_t& v1, const nbcoord_t mass1) const { nbvertex_t total_force; size_t curr = NBODY_HEAP_ROOT_INDEX; size_t tree_size = m_mass_center.size(); do { const nbcoord_t distance_sqr((v1 - m_mass_center[curr]).norm()); if(distance_sqr > m_radius_sqr[curr]) { total_force += force(v1, m_mass_center[curr], mass1, m_mass[curr]); curr = skip_down(curr); } else { curr = next_up(curr, tree_size); } } while(curr != NBODY_HEAP_ROOT_INDEX); return total_force; }

总共，我们得到了树遍历和力计算的六个组合。比较这些方法的计算时间和质量。我们将经过100次迭代后系统总能量的相对变化作为质量度量。作为模型系统，我们采用两个相互作用的“星系”

每个

尸体。表4.树木遍历方法和力计算的组合

$16384$

树遍历/力计算类型	树与堆栈	堆的“堆”	没有堆的“堆”
按主体编号进行迭代	循环+树	循环+堆	周期+无堆
叶旁路	nestedtree +树	nestedtree +堆	嵌套树+无堆


a）函数计算时间依赖性 $f_n$ 从到树节点的关键距离到它的半径的比率（ $\lambda_{crit}$ ）。	b）系统中能量的相对变化对到树节点的临界距离与其半径之比的依赖关系（ $\lambda_{crit}$ ）。
图10. 函数计算结果 $f_n$ 各种方式在CPU上（主体数 $N=32768$ ）

可以看出，“嵌套树+树”的实现速度毫无希望地落后，因为它缺乏并发性。最重要的是实现在数组中具有树节点的位置并在二进制堆中建立索引的实现。能量的相对变化对于所有具有

$\lambda_{crit} > 1$ 。同样在图。图10a显示了

），所有实施例函数运算

$\lambda_{crit} < 10$

大大超过了精确计算的最优化版本（“ openmp +块+优化”），并且进一步提高了速度

$f_n$

树木损失精度版本的实现。

$\lambda_{crit}$

GPU树遍历

我尝试使用OpenCL技术和CUDA绕过GPU上的树。以树形式存储节点的选项被立即丢弃，仅剩下将树存储在具有索引的数组中的选项，如在二进制堆中那样。通常，计算核心的实现与CPU版本没有太大区别。

OpenCL ( )

 __kernel void ComputeTreeBH(int offset_n1, int points_count, int tree_size, __global const nbcoord_t* y, __global nbcoord_t* f, __global const nbcoord_t* tree_cmx, __global const nbcoord_t* tree_cmy, __global const nbcoord_t* tree_cmz, __global const nbcoord_t* tree_mass, __global const nbcoord_t* tree_crit_r2) { int n1 = get_global_id(0) + offset_n1; int stride = points_count; __global const nbcoord_t* rx = y; __global const nbcoord_t* ry = rx + stride; __global const nbcoord_t* rz = rx + 2 * stride; __global const nbcoord_t* vx = rx + 3 * stride; __global const nbcoord_t* vy = rx + 4 * stride; __global const nbcoord_t* vz = rx + 5 * stride; __global nbcoord_t* frx = f; __global nbcoord_t* fry = frx + stride; __global nbcoord_t* frz = frx + 2 * stride; __global nbcoord_t* fvx = frx + 3 * stride; __global nbcoord_t* fvy = frx + 4 * stride; __global nbcoord_t* fvz = frx + 5 * stride; nbcoord_t x1 = rx[n1]; nbcoord_t y1 = ry[n1]; nbcoord_t z1 = rz[n1]; nbcoord_t res_x = 0.0; nbcoord_t res_y = 0.0; nbcoord_t res_z = 0.0; int stack_data[MAX_STACK_SIZE] = {}; int stack = 0; int stack_head = stack; stack_data[stack++] = NBODY_HEAP_ROOT_INDEX; while(stack != stack_head) { int curr = stack_data[--stack]; nbcoord_t dx = x1 - tree_cmx[curr]; nbcoord_t dy = y1 - tree_cmy[curr]; nbcoord_t dz = z1 - tree_cmz[curr]; nbcoord_t r2 = (dx * dx + dy * dy + dz * dz); if(r2 > tree_crit_r2[curr]) { if(r2 < NBODY_MIN_R) { r2 = NBODY_MIN_R; } nbcoord_t r = sqrt(r2); nbcoord_t coeff = tree_mass[curr] / (r * r2); dx *= coeff; dy *= coeff; dz *= coeff; res_x -= dx; res_y -= dy; res_z -= dz; } else { int left = left_idx(curr); int rght = rght_idx(curr); if(left < tree_size) { stack_data[stack++] = left; } if(rght < tree_size) { stack_data[stack++] = rght; } } } frx[n1] = vx[n1]; fry[n1] = vy[n1]; frz[n1] = vz[n1]; fvx[n1] = res_x; fvy[n1] = res_y; fvz[n1] = res_z; }

, , GPU. , , , .. . , , , , , , tn1.

OpenCL ( )

 __kernel void ComputeHeapBH(int offset_n1, int points_count, int tree_size, __global const nbcoord_t* y, __global nbcoord_t* f, __global const nbcoord_t* tree_cmx, __global const nbcoord_t* tree_cmy, __global const nbcoord_t* tree_cmz, __global const nbcoord_t* tree_mass, __global const nbcoord_t* tree_crit_r2, __global const int* body_n) { int tree_offset = points_count - 1 + NBODY_HEAP_ROOT_INDEX; int stride = points_count; int tn1 = get_global_id(0) + offset_n1 + tree_offset; int n1 = body_n[tn1]; nbcoord_t x1 = tree_cmx[tn1]; nbcoord_t y1 = tree_cmy[tn1]; nbcoord_t z1 = tree_cmz[tn1]; nbcoord_t res_x = 0.0; nbcoord_t res_y = 0.0; nbcoord_t res_z = 0.0; int stack_data[MAX_STACK_SIZE] = {}; int stack = 0; int stack_head = stack; stack_data[stack++] = NBODY_HEAP_ROOT_INDEX; while(stack != stack_head) { int curr = stack_data[--stack]; nbcoord_t dx = x1 - tree_cmx[curr]; nbcoord_t dy = y1 - tree_cmy[curr]; nbcoord_t dz = z1 - tree_cmz[curr]; nbcoord_t r2 = (dx * dx + dy * dy + dz * dz); if(r2 > tree_crit_r2[curr]) { if(r2 < NBODY_MIN_R) { r2 = NBODY_MIN_R; } nbcoord_t r = sqrt(r2); nbcoord_t coeff = tree_mass[curr] / (r * r2); dx *= coeff; dy *= coeff; dz *= coeff; res_x -= dx; res_y -= dy; res_z -= dz; } else { int left = left_idx(curr); int rght = rght_idx(curr); if(left < tree_size) { stack_data[stack++] = left; } if(rght < tree_size) { stack_data[stack++] = rght; } } } __global const nbcoord_t* vx = y + 3 * stride; __global const nbcoord_t* vy = y + 4 * stride; __global const nbcoord_t* vz = y + 5 * stride; __global nbcoord_t* frx = f; __global nbcoord_t* fry = frx + stride; __global nbcoord_t* frz = frx + 2 * stride; __global nbcoord_t* fvx = frx + 3 * stride; __global nbcoord_t* fvy = frx + 4 * stride; __global nbcoord_t* fvz = frx + 5 * stride; frx[n1] = vx[n1]; fry[n1] = vy[n1]; frz[n1] = vz[n1]; fvx[n1] = res_x; fvy[n1] = res_y; fvz[n1] = res_z; }

. . , , , .. , . , , , , , , . , , . 即当遍历树的其余部分时，计算核心的相邻线程不会访问树的相同节点，而是紧密位于内存中。要优化此内存访问，可以使用纹理内存。但是有一个障碍。目前，纹理不支持使用双精度数据（我们要精确计算）。但是在CUDA中，有一个__hiloint2double函数，它从两个整数中收集一个双精度数。

来自存储整数的纹理的双精度数字请求代码

 template<> struct nb1Dfetch<double> { typedef double4 vec4; static __device__ double fetch(cudaTextureObject_t tex, int i) { int2 p(tex1Dfetch<int2>(tex, i)); return __hiloint2double(py, px); } static __device__ vec4 fetch4(cudaTextureObject_t tex, int i) { int ii(2 * i); int4 p1(tex1Dfetch<int4>(tex, ii)); int4 p2(tex1Dfetch<int4>(tex, ii + 1)); vec4 d4 = {__hiloint2double(p1.y, p1.x), __hiloint2double(p1.w, p1.z), __hiloint2double(p2.y, p2.x), __hiloint2double(p2.w, p2.z) }; return d4; } };

, (x, y, z, tree_crit_r2) , . , r2 > tree_crit_r2[curr] , . CUDA L1 ( cudaFuncSetCacheConfig ). , L1 .

CUDA ( )

 __global__ void kfcompute_heap_bh_tex(int offset_n1, int points_count, int tree_size, nbcoord_t* f, cudaTextureObject_t tree_xyzr, cudaTextureObject_t tree_mass, const int* body_n) { nb1Dfetch<nbcoord_t> tex; int tree_offset = points_count - 1 + NBODY_HEAP_ROOT_INDEX; int stride = points_count; int tn1 = blockDim.x * blockIdx.x + threadIdx.x + offset_n1 + tree_offset; int n1 = body_n[tn1]; nbvec4_t xyzr = tex.fetch4(tree_xyzr, tn1); nbcoord_t x1 = xyzr.x; nbcoord_t y1 = xyzr.y; nbcoord_t z1 = xyzr.z; nbcoord_t res_x = 0.0; nbcoord_t res_y = 0.0; nbcoord_t res_z = 0.0; int stack_data[MAX_STACK_SIZE] = {}; int stack = 0; int stack_head = stack; stack_data[stack++] = NBODY_HEAP_ROOT_INDEX; while(stack != stack_head) { int curr = stack_data[--stack]; nbvec4_t xyzr2 = tex.fetch4(tree_xyzr, curr); nbcoord_t dx = x1 - xyzr2.x; nbcoord_t dy = y1 - xyzr2.y; nbcoord_t dz = z1 - xyzr2.z; nbcoord_t r2 = (dx * dx + dy * dy + dz * dz); if(r2 > xyzr2.w) { if(r2 < NBODY_MIN_R) { r2 = NBODY_MIN_R; } nbcoord_t r = sqrt(r2); nbcoord_t coeff = tex.fetch(tree_mass, curr) / (r * r2); dx *= coeff; dy *= coeff; dz *= coeff; res_x -= dx; res_y -= dy; res_z -= dz; } else { int left = nbody_heap_func<int>::left_idx(curr); int rght = nbody_heap_func<int>::rght_idx(curr); if(left < tree_size) { stack_data[stack++] = left; } if(rght < tree_size) { stack_data[stack++] = rght; } } } f[n1 + 3 * stride] = res_x; f[n1 + 4 * stride] = res_y; f[n1 + 5 * stride] = res_z; }

对nvprof分析器中的程序进行的分析表明，即使使用纹理内存存储树，全局内存上的负载仍然非常高。

实际上，在CUDA中，所有寻址到“计算出的”地址的内核内存都存储在全局内存中，因此，遍历树所需的堆栈位于全局内存中，并且吞噬了内存芯片带宽的很大一部分，因为该堆栈具有每个运行线程，并且有很多线程。

但是，幸运的是，我们已经知道如何在不使用堆栈的情况下遍历树。用计算下一个树节点的功能对先前的计算核心进行补充，我们得到了一个新的内核，而且更加紧凑。

CUDA核心，无需遍历堆栈即可遍历树来计算强度

 __global__ void kfcompute_heap_bh_stackless(int offset_n1, int points_count, int tree_size, nbcoord_t* f, cudaTextureObject_t tree_xyzr, cudaTextureObject_t tree_mass, const int* body_n) { nb1Dfetch<nbcoord_t> tex; int tree_offset = points_count - 1 + NBODY_HEAP_ROOT_INDEX; int stride = points_count; int tn1 = blockDim.x * blockIdx.x + threadIdx.x + offset_n1 + tree_offset; int n1 = body_n[tn1]; nbvec4_t xyzr = tex.fetch4(tree_xyzr, tn1); nbcoord_t x1 = xyzr.x; nbcoord_t y1 = xyzr.y; nbcoord_t z1 = xyzr.z; nbcoord_t res_x = 0.0; nbcoord_t res_y = 0.0; nbcoord_t res_z = 0.0; int curr = NBODY_HEAP_ROOT_INDEX; do { nbvec4_t xyzr2 = tex.fetch4(tree_xyzr, curr); nbcoord_t dx = x1 - xyzr2.x; nbcoord_t dy = y1 - xyzr2.y; nbcoord_t dz = z1 - xyzr2.z; nbcoord_t r2 = (dx * dx + dy * dy + dz * dz); if(r2 > xyzr2.w) { if(r2 < NBODY_MIN_R) { r2 = NBODY_MIN_R; } nbcoord_t r = sqrt(r2); nbcoord_t coeff = tex.fetch(tree_mass, curr) / (r * r2); dx *= coeff; dy *= coeff; dz *= coeff; res_x -= dx; res_y -= dy; res_z -= dz; curr = nbody_heap_func<int>::skip_idx(curr); } else { curr = nbody_heap_func<int>::next_up(curr, tree_size); } } while(curr != NBODY_HEAP_ROOT_INDEX); f[n1 + 3 * stride] = res_x; f[n1 + 4 * stride] = res_y; f[n1 + 5 * stride] = res_z; }

, GPU, , . , , . , , , , . . NVidia K80.

5. ( )

$f_n$ GPU

$N=131072$

$\lambda_{crit}=10$

/	8	16	32	64	128	256	512	1024
opencl+dense	5.77	2.84	1.46	1.13	1.15	1.14	1.14	1.13
cuda+dense	5.44	2.55	1.27	0.96	0.97	0.99	0.99	--
opencl+heap+cycle	5.88	5.65	5.74	5.96	5.37	5.38	5.35	5.38
opencl+heap+nested	4.54	3.68	3.98	5.25	5.46	5.41	5.48	5.31
cuda+heap+nested	3.62	2.81	2.68	4.26	4.84	4.75	4.8	4.67
cuda+heap+nested+tex	2.6	1.51	0.912	0.7	1.85	1.75	1.69	1.61
cuda+heap+nested+tex+stackless	2.3	1.29	0.773	0.5	0.51	0.52	0.52	0.52

6. ( )

$f_n$ GPU

$N=1M$

$\lambda_{crit}=4$

块大小/核心	8	16	32	64	128	256	512	1024
opencl +密集	366	179	89.9	69.3	70.3	69.1	68.9	68.0
CUDA +密集	346	162	79.6	60.8	60.8	60.7	59.6	--
opencl +堆+周期	16.2	18.2	20.1	21.2	21.2	21.3	21.2	21.1
opencl +堆+嵌套	10.5	7.63	6.38	8.23	9.95	9.89	9.65	9.66
CUDA +堆+嵌套	8.67	6.44	5.39	5.93	8.65	8.61	8.41	8.27
CUDA +堆+嵌套+ TEX	6.38	3.57	2.13	1.44	3.56	3.46	3.30	3.29
cuda +堆+嵌套+ tex +无堆栈	5.78	3.19	1.83	1.21	1.11	1.10	1.11	1.13

这是一个困难的情况，但是与树遍历的CPU版本不同，很明显，每个优化步骤都会带来切实的结果。与完全函数计算的精确解决方案相比，“ opencl +堆+周期”的实现慢了近6倍

$f_n$ 。 'opencl+heap+nested', , 1.4 , .. . 'cuda+heap+nested' L1 , 1.4 , , cuda ( 'opencl+dense' 'cuda+dense' , cuda ~1.2 ). ( 3.8 ) . 'cuda+heap+nested+tex+stackless' 1.4 , .. . ,

$\lambda_{crit}=10$

$f_n$ 。但是

$\lambda_{crit}=10$ , CPU ,

$\lambda_{crit}$ .

$\lambda_{crit}$ , .


a) $N=128K$	b） $N=1M$
图11. 函数计算时间的依赖性。 $f_n$ 从到树节点的关键距离到它的半径的比率（ $\lambda_{crit}$ 关于各种GPU遍历的实现）

可以看出，对于小

计算特征的所有方法

$\lambda_{crit}$

接近于关闭值，该值由构造kd-tree和准备GPU数据时确定。此外，植树的时间对

$f_n$

$\lambda_{crit}\leq 4$ , . ,

$N=128K$

$\lambda_{crit}=1024$ , , GPU , L1 'branch divergence' . , (cuda+heap+nested+tex+stackless),

倍。其他实现则慢了好几倍。为了合并结果，我们将在具有更新架构的GPU上计算时间。

$1.4-1.5$

GeForce GTX 1080 Ti的发布结果（单精度）

7. ( )

$f_n$ GPU

$N=1M$

$\lambda_{crit}=4$

/	8	16	32	64	128	256	512	1024
opencl+dense	47.8	23.4	11.6	11.59	12.8	12.8	12.8	12.8
cuda+dense	49.0	23.8	11.9	11.8	11.7	11.7	11.7	11.7
opencl+heap+cycle	7.48	8.26	7.73	7.36	7.33	7.27	7.25	7.26
opencl+heap+nested	1.33	1.20	1.41	2.46	2.53	2.49	2.44	2.47
cuda+heap+nested	1.23	1.10	1.31	2.28	2.29	2.28	2.23	2.25
cuda+heap+nested+tex	0.88	0.68	0.654	1.6	1.6	1.6	1.6	1.6
cuda+heap+nested+tex+stackless	0.71	0.47	0.45	0.43	0.43	0.42	0.41	0.395

12.

$f_n$ (

$\lambda_{crit}$ ) GPU

GeForce GTX 1080 Ti , , , . , GPU . 5-7 , GPU, , , . , .

, — (

$2^{20}$ ) , GPU. GPU (Tesla V100), , , .. , Tesla K80. , , , , , .

结论

, . , « »,

$N$ , , .

可视化

, .

. 60 .

模拟由一百万颗恒星组成的星系的演化。中心是质量总计为99％的物体。单个颗粒几乎无法区分。已经更像一滴液体中的波浪。根据速度模块着色。低速-蓝色，中-绿色，高-红色。可以看出，在中心速度较高，并逐渐减小到边缘，而在赤道面最低。

百万星系演化的更“动态”模拟。中心是质量占总质量10％的物体。中央身体对其余部分的影响明显较小。首先，“星星”飞散，然后聚集成几个星团，最后又形成一个大星团。

在建模过程中，约有5％的“星星”不可撤销地离开了初始区域。

在第十秒，它非常类似于现有的车轮星系。

项目代码可以在github上找到。

N个物体的任务或如何在不离开厨房的情况下炸毁星系

现象的物理

数学

总结

CPU实施

GPU实施

Opencl的

库达

函数近似 fn f_n

GPU树遍历

结论

可视化

More articles:

函数近似 $f_n$