👩🏽‍🍳 🤚🏾 😰 五子棋的制胜法宝-35招 🎗️ 🚶🏼 👎🏾

按照标准的Gomoku规则进行比赛时，Black最多只需要获得35步即可获胜。本文向您介绍了完整的获胜策略和相应的游戏算法。

完整解决方案的演示- 在这里 -您可以玩耍并找到最长的选择。该程序始终获胜，并在其上花费不超过35个动作。该应用程序的源代码，解决方案本身以及本文末尾的各方示例。

我不会讲游戏的规则和策略。在这里，有关habr以及此处和此处的决策算法详细讨论了该主题。

小题外话

在智能手机时代之前，井字游戏“连续五个”（Renju的Gomoku）是当时学校课程中最受欢迎的杀手之一。与北非国民经济的发展或三叶草花的分类相比，考虑组合更为有趣。

1985年秋天，我们10年级的女孩上了数学课。我们，剩下的六个孩子，最有可能与数学老师就抽象主题进行非正式交流。老师默默地进入教室，将传单分发给每个人放在盒子里，然后开始在黑板上写下那些人的名字。我们感到沮丧，计划独立工作或计划进行闪电调查。但是董事会名单变成了排名，我们宣布了锦标赛的规则。每个系列各有五方。获胜者得奖-杂志获得五奖。根据比赛的结果，我很幸运获胜，但是比赛并没有就此结束。老师承诺如果获胜者连续赢得系列赛的全部五场比赛，则向所有人提供五分球。第一步的权利授予了获胜者。与我们老师的断言相反，在这种情况下，如果游戏正确，您可以连续赢得10、100或任意数量的游戏，那么胜利对我来说似乎是不可思议的运气。

九年后的1994年，Lewis Victor Allis博士在Go-Moku和Threat-Space Search的一篇文章中阐述了这一假设的证据。作者没有发布他的获胜策略，这使他可以验证证据。但是，在他1996年的《在游戏和人工智能中寻找解决方案》一书中，对算法进行了一般性描述。总之，我们分别提到了检查获胜策略是否完整的过程，该过程依赖于“威胁序列”搜索算法的正确实施以及对对手反击选择的分析。

文章和书中给出的解决方案示例是对手获胜策略的一部分，其中包括对手的“正确举动”，这证明了所使用算法的弱点。

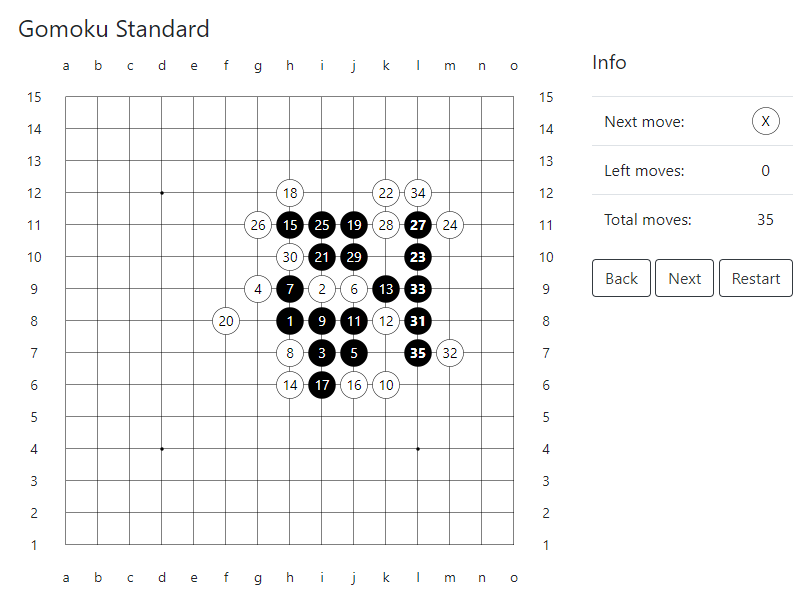
例如，在图中，是标准Gomoku规则的程序解决方案。如果黑方先回应j10，然后j8回应白方的第10步g9，则游戏以29步而不是45结束。然后，该程序两次“没有注意到”黑方的“威胁序列”组合，分别是16步和26-之后的17步。怀特的举动。最后，如果怀特做出第36步f12而不是j12，他将至少坚持到第49步。公平地说，在这个例子中，所有黑方的举动都不会给白方留下任何以他的优势结束比赛的机会。

在互联网上，我找到了一些类似作品的参考文献，以寻找成功的策略。找到的解决方案的最优性问题仍然没有解决。布莱克需要获胜的最少举手次数是多少？

因此，在难忘的学校冠军赛结束33年后，他有了一点空闲时间，现代化的计算资源，并向儿童的爱好致敬，他的任务是为Gomoku中的Black寻找最佳的获胜策略。

数字化董事会上的职位

录制零件非常原始。场上只有225个牢房。因此，每个单元被1字节编码。要记录一批35次移动，仅需要35个字节。但是，由于以下两个原因，这样的记录不适合进行位置评估：可以以不同的移动顺序获得相同的位置，并且不考虑对称位置。

实现游戏的目标-连续建造五块石头-可以在四个方向之一上进行：垂直，水平和两个对角线。因此，我们可以将任何位置表示为一组线。长度为15个像元的水平和垂直线，长度为1到15个像元的对角线。每次移动都会同时沿不同方向更改4条线的值。

评估职位的任务是确定每一行的所有有效数字。为简单起见，我们用2位描述该行的每个单元。安装白色石头时，第一位已满，第二位是黑色。每行包含不超过15个单元，并被编码为32位整数。因此，减少了在线上对形状的搜索，以将通过滑动窗口的线的数值与该形状的位图案进行比较。

在图中所示的示例中，位置用26条线描述。因此，它用104个字节编码，而常规批处理记录仅需要17个字节。
很容易猜到，所有对称性（转弯和镜像）都是通过简单地改变线条的数量（改组）和方向来获得的。为了识别位置并快速搜索集合，此原理实现了32位哈希函数，该函数仅为非对称位置提供不同的值。

对称的使用大大减少了所考虑的位置数量。例如，第二步的选项数量从224减少到35。

搜索解决方案和组合时（将在下面进行讨论），计算出的位置将构成多层图的顶点。根据填充单元的数量将顶点分为几层。这些移动组成了图形的边缘，连接了相邻图层的顶点。如果在搜索过程中放弃不成功的移动，则会删除边，并且某些顶点将失去与主分支的连接。因此，在计算步骤之后，将执行垃圾收集（或从顶部重建图形）。

在开发过程中，考虑了几种编码算法，但上述一种算法显示出最高的位置估计率。

评估位置

评估位置的重要因素是对手建立重要部分的重要性。

五 -如果在棋盘上找到这样的棋子，游戏就结束了。对于标准规则，不要使用六，七等，请给Gomoku奖励。因此，与其他所有数字一样，这五个数字要求在行中的相邻单元格上没有它们的石头。

开放的四个 -6个单元格的长度，中间的四个被相同颜色的石头占据，外面的一定是空的。好吧，至于五个，它们的石头在邻近的牢房中不存在。一个非常强大的数字意味着即使在别人的举动下也能获胜。

四个 -5个单元格的长度，五个单元格中的一个（任意）是空闲的。自己赢得胜利。它造成了威胁，并迫使对手在没有四人的情况下在自由区中移动。防守中给予该位置等级5分。

一个开放的三元组 -长度为6或7个单元，最外面的单元必然是自由的。对于6个牢房，四个中间牢房中的三个被相同颜色的石头占据，一个空闲。对于7个单元格-三个中等大小的单元格被相同颜色的石头占据。如果对手没有四分之一或三分开放，则该棋子依次变为四分之一开。在其他人的举动下，它会造成威胁，并迫使对手关闭三局或将其四局作为回应。第6个单元格的三步有1个上升动作和3个闭合动作。第7个单元格三步有2个上升动作，只有2个闭合动作。在位置评分中获得2到4分。

一个三元组或一个封闭的三元组是5个单元格的长度，其中任何三个都被相同颜色的石头占据。轮到的三人可以变成四人，用于进攻和防守，比对手的空位三人产生的威胁更大。给出1分的位置评分。

一个开放的 （透视的）演习 -从6到7个细胞长。攻击时，将转换为公开三级。在位置评分中给出1或2分。

堵塞是同时无法一次性关闭的两个或多个威胁。有3x3的叉子（两个三开的三叉），3x4的叉子（三开和四）和4x4的叉子（两个开四），如果对手没有更大的威胁，则叉子将获胜-3x3的叉子为四或三开，否则对手无法连续关闭叉子，造成巨大威胁-3x3叉的顺序为四。

组合 -连续一系列的威胁和防御，以对抗对手的更大威胁，从而为玩家带来积极的结果。组合是进攻（或获胜）和防守。

如果在对手的任何防御或进攻行动中，发现响应动作导致获胜，则进攻或获胜组合成功。进攻组合的结尾是安装了插头，对手无法将其关闭。

相反，当对手停止制造威胁或超过计算的移动限制时，防御性组合才成功。防守组合包括防守动作或对对手造成更大的威胁。

当评估位置时，执行对获胜组合的搜索。如果成功，我们就赢了。否则，如果没有对手的威胁，则状态为中立。如果对手有威胁，我们会寻找防守组合。如果成功，则状态是中立的；如果失败，则我们将丢失。

由于攻击和强迫报复行动的选择数量非常有限，因此允许搜索足够大的深度的组合。在最佳策略的初始构建期间，在25个动作中建立了组合搜索的允许深度。重新计算用于在javascript中实现位置估算算法的解决方案时，允许的搜索深度减少到17个移动。
在计算最佳策略时，从上方获胜组合的搜索深度还受到目标最大移动次数的限制。

我们正在寻找解决方案

因此，我们将给定位置定为中立，然后选择下一步。在这种情况下，我们的行为取决于我们是攻击方还是防御方。对于进攻端，完整的解决方案将是一系列动作，在该动作中，对于任何对手的返回动作，该位置将被评估为获胜（找到获胜组合），或者在解决方案中包含下一个自己的动作。值得注意的是，计算最佳策略时，进攻方总是黑色，防守方是白色。

攻击方只需要找到一招，即可取得最快的胜利。在缺乏资源的情况下，攻击者人为地限制了破获选择的数量，我首先研究了导致得分最高的位置的举动。找到任何解决方案后，攻击者会沿着最长的解决方案扩展选择范围，探索较少的额定位置，以缩短解决方案的长度。

对于防守方来说，找到一个单步动作就足够了，在给定的动作极限内，单步动作不会导致对手获胜。所有空闲单元格都可用于枚举。
为了减少要分类的移动次数，我们使用“跳过”算法。我们跳过防守动作，寻找成功的进攻组合。如果成功，则可能的防御动作可能仅限于影响找到的组合成功的动作。平均而言，这使您可以在每个步骤中将搜索区域缩小4-6倍。请注意，在被忽略的动作中，解决方案的分支可能更长。因此，为了搜索最佳解，“跳过”算法仅在初始搜索中使用。

我们计算策略

所有组件都准备就绪，我们将第一块黑石头放在战场的中心，开始寻找解决方案，然后……在此之后的几个小时，我的笔记本电脑的资源用尽了，我不得不承认“在战斗中，而不是在战斗中”失败。

实际上，我拥有一百五十个Xeon内核和TB的可用RAM触手可及的计算能力。但是，请记住，在90年代中期，Allis在128 MB的RAM上每个只有10个SUN SPARCstation 2，对不喜欢运动的行为感到re悔，并决定将Java机器上的RAM数量限制为1 GB，并且仅为该任务分配了1个线程处理器。与它的MHz相比，它可以以某种方式补偿我的GHz。另外，他承诺在工作结束时将浏览器的算法转换为javascript。

因此，搜索策略必须从首次登台草图的决定开始。萨加尔的着名著作《从首次亮相到中级游戏》以及米哈伊尔·科钦和亚历山大·诺索夫斯基的《石头环》中都可以找到有关俄罗斯Renju游戏首次亮相的详细说明。这些书已经有20年的历史了，但是从那以后很少出版这类文献。不幸的是，2015年Dmitry Epifanov的最新作品“关在笼子里的老虎”无法以电子形式获得。

根据以下算法进行最佳开放决策的搜索。第一步，在不限制批次长度的情况下进行了初步计算。然后，对于最长的解决方案，进行了优化：将找到的组合替换为用于最终步骤的较短解决方案，并为所有中间步骤搜索较短的决策分支。进行优化，直到解决方案的所有分支均达到目标极限。然后，目标极限降低，并尝试将其优化为新值。

图3中的第三个垂直首次亮相没有问题。结果是一整套解决方案。结果，第四步i8和j10之后最困难的位置解决了31个步。然后设定了每局35步的目标限制。

从对角线的决定，他传统上选择了第七次登场。最困难的位置出现在第四步g9之后。找到了6个动作g8和g7的允许长度解。

但是对于此选项，随着j9上的第6步移动，我无法找到比33步短的解决方案。那几乎是一场灾难。出于绝望，我尝试了第五种替代方案以及所有其他类型的对角线开口的解决方案。首次亮相得到解决，但没有发现每场比赛少于39步的动作。

回到最初的第7条对角线处子秀时，他重新编写了用于生成攻击动作语句的算法。结果，导致得分排在前十名的位置的移动意外地开始产生结果并缩短了求解路径的长度。如此数量的计算的可变性变得相当大。解决深度为12步时，有超过200万个职位（不包括搜索组合时的职位）。继续取决于为任务分配的1GB RAM。因此，为了检查对最终分叉的决定，在某些情况下，有必要从第18步移动中分别确定位置。

在第七次对角线处子秀中以35个动作决定了胜利之后，一个人可以庆祝胜利-为中锋而战。前面仍然有大量例行计算工作，需要通过“非最佳”白棋计算来完成该策略。在最佳策略的总数量中，结果是此类举动的答案是80％。幸运的是，在第二步之后，它们在初步计算中被完全自动解决，并且所有这些体积在几天之内被添加到了最佳策略中。

因此，找到了所有两个动作的解决方案。我们将第一块黑石头放在场地中央，开始寻找解决方案，甚至没有时间感觉到这一刻的重要性-最初的位置用35个动作解决了。建立了最佳获胜策略的图表。

检查自己

下一步是验证解决方案。完全关闭防御方的情报。黑棋每走一步，白棋就会移至棋盘的任意方块。 White的举动之后获得的位置必须在决策图中找到，或者被评估为获胜的举动数目，其起步数不超过起始位置的最长分支。在评估每个位置时，我们会先检查找到的获胜组合，以找出白方所有可允许的举动，然后黑方才能构建最终的棋段-连续五局。

进行了几次检查直到完成。最后的无错误运行在单线程模式下花费了14个小时。在检查过程中，发现并纠正了错误，这些错误是由于搜索组合的深度，跳动的假设，对称位置的重复而产生的。

回答问题-是35个动作中的决定确实是最佳的。根据我的研究，对于垂直首次亮相中最长的分支，可以找到长度为33个动作的更理想的解决方案。但是对于在j9上进行第6次移动后的对角线，要花费大量时间来寻找33个移动中的解，Black的变化在每个步骤中扩展到50个移动，无济于事。无法严格证明33个动作中没有解决方案，为该项目分配的时间已经结束，并且决定停止在35个动作的目标极限上。