游戏失误的数学模型

阅读难度

• 我太年轻了

  
  
  • 简介和游戏规则
  • 他们是如何做到的？
  • Dobble的事件矩阵
  • 游戏中缺少哪两张牌？
  • 为什么有2张牌比游戏中的最大张数少？
  • 致谢
  
  

• 让我聪明

  
  
  • 简介和游戏规则
  • 他们是如何做到的？
  • 该卡与它有什么关系？
  • 小订单的投影飞机
  • Dobble的事件矩阵
  • 游戏中缺少哪两张牌？
  • 为什么有2张牌比游戏中的最大张数少？
  • 致谢
  
  

• 梦m

  
  
  • 简介和游戏规则
  • 他们是如何做到的？
  • 婴儿的最终几何形状
  • 该卡与它有什么关系？
  • 小订单的投影飞机
  • 如何建造投影飞机？
  • Dobble的事件矩阵
  • 游戏中缺少哪两张牌？
  • 为什么有2张牌比游戏中的最大张数少？
  • 致谢
  
  

简介和游戏规则

几年前，我买了游戏Dobble （ Dobble ，原名“ Spot It！”）。 这是一个非常简单，快速且有趣的游戏，我认为它是总体上最好的棋盘游戏之一。

游戏中有55张卡片，每张卡片上都有8个不同的符号。 这些卡的外观如下：

图 1.游戏卡示例。

在每两张卡上，只有一个符号匹配。 在上图中，这是铅笔符号：

图 2.匹配卡片上的字符。

第一次看到比赛的玩家根据其中一轮的比赛对其中一张牌进行操作。 例如，将其拿给自己或扔给对手。
通常这会导致以下事实：玩家正在寻找比赛的一张牌正在改变。 因此，您必须寻找新的匹配项，这可能是一个完全不同的符号：

图 3，4 .第一张卡被替换为新卡。 现在它们之间有了新的巧合-小丑的象征。

他们是如何做到的？

乍一看，在两张牌上恰好是一个巧合，这似乎是不可思议的，不多也不少。 问题立即出现-游戏中有多少个角色？ 它们不能太少（那么卡上将有多个匹配项）或太多（那么卡上可能没有任何匹配项）。
另外，很明显，符号以特殊顺序位于卡上，这保证了任何两张卡的唯一匹配。

Google的基本技能将我们带到stackoverflow网站，该网站描述了发生这种情况的原因： http ： //stackoverflow.com/questions/6240113/what-are-the-mathematical-computational-principles-behind-this-game

该游戏使用有限几何原理。 尽管此短语中有“几何”一词，但该概念更多地是指组合数学，而不是几何。 它以有限数量的点进行操作，这些点尤其可以以投影平面的形式定位。

游戏中的卡牌和符号是7阶投影平面的元素。 这意味着每张卡上都有n +1个符号，游戏中唯一符号的总数为n ^ 2 + n +1 ，即 57个字符。

有较低和较高等级的飞机。 例如，有一个五阶平面。 对于她来说，卡上显示6个符号，游戏中唯一符号的总数为5 ^ 2 + 5 + 1 =31。此配置的投影平面用于游戏Doble的更简单版本中，称为“ Doble 1,2,3” 。

使用入射矩阵设置投影平面点与线之间的连接。 它的外观在“游戏Dobble的事件矩阵”部分中给出。

婴儿的最终几何形状

比起撰写原始文章要晚得多，我参加了Alexei Savvateev的演讲，他谈到了射影几何更短，更易于理解。 但是，由于这个原因，我没有实力或欲望重写本文的一半，所以我只推荐他的书《人文数学》，如果我用野蛮的方式来解释汽车在手指上的装置是难以理解或无聊的。

首先，转到Wikipedia并阅读一些文章。 第一篇文章介绍了有限几何的概念：

有限几何是具有有限数量点的任何几何系统。 [1]

到目前为止，一切都很简单。 如果用笔在纸上画几个点，那么它们将已经构成某种有限的几何形状。
惊喜还在等待着更多：

例如， 欧几里得几何形状不是有限的，因为欧几里得线包含无限数量的点，或者确切地说，其包含的点数与实数一样多 。 [1]

对我们来说，这意味着在其上绘制点的纸不是有限几何形状的平面 。 它只是一个点载体。

平面上有两种类型的几何： 仿射和射影 。 在仿射几何中，通常使用直线的平行度概念。 [1]

回忆一下公理描述仿射几何：

平面上的仿射几何是一个非空集合X （其元素称为“点”），具有L个X子集（其元素称为“直接”）的非空集合，使得：

1. 对于两个不同的点，只有一条线包含两个点。
2. 对于线ℓ和不属于ℓ的点p ，存在一条并且只有一条线p '包含p ，使得ℓ∩∩ ' =∅。
3. 四个点很多，没有一个在同一行。 [1]

这些公理使我们有机会了解有限几何中最简单的仿射平面是什么样的：

最简单的仿射平面仅包含4个点，称为二阶仿射平面 。 每对点定义一条唯一的线，因此指示的平面包含6条线。 [1]

不太清楚吗？ 没错 如果仔细观察仿射几何的定义，您会发现它与集合论（元素，集合，子集）的概念一起运行。
这意味着这些线看起来可能根本不像欧几里得几何的常规线。

其实是。 如果您查看二阶仿射平面的图片，我们将看到以下图片：

图 5.雅典平面的二阶。 （来源ru.wikipedia.org ）

这里的点看起来像普通的黑点，但是直线是多色的线段。 相同颜色的线被认为是平行的。

如您所见，这里的线不是无限长的。 秘密地说，我要说的是这里根本没有长度的概念，直线可以有任何形状，我们很快就会看到。

当然，％用户名％还怀疑该平面的图像是否满足仿射几何公理。 让我们检查一下：

1. 我们取2个任意点，例如左上和左下。
   这两个点仅包含一条左红线。
   右边的红线不包含任何这些点，其余的线仅包含其中一个。
2. 取左红色直线和右上点。 显然，只有一条直线（右红色）平行于左红线，因为它穿过右上点，但没有穿过左两个点中的任何一个。
3. 该图清楚地表明，无论我们取3点，其中一个都位于与其他两个点所在的线不同的线上。
   组成正方形对角线的两条线不相交，因为它们没有公共点。

如果您很好地理解了上一张图片的内容，那么该图片会更加复杂：

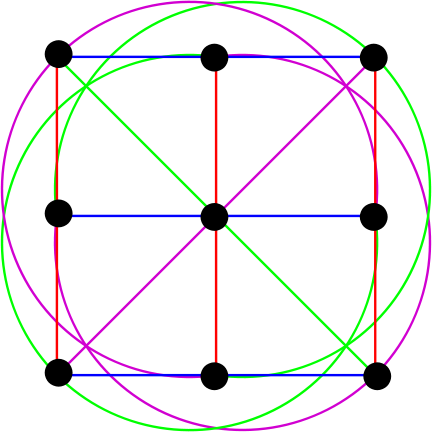
图 6.雅典平面的三阶。 （来源ru.wikipedia.org ）

在这里我们看到9点和12条线。 是的，％用户名％，就有限的几何形状而言，这些椭圆实际上是直线。
相同颜色的形状是平行线。 它们很难被发现，因此我们将图片分为几部分：

1号飞机	2号飞机	3号飞机	飞机号4

图 7.三阶仿射平面的平行直线。

在这里，检查公理的执行将花费更长的时间：

1. 我们取2分，例如中央右上和右下。 通过它们的只有紫色线之一。
2. 取左红线和右下点。 与二阶平面相似，只有一条右红线穿过该点，但没有穿过左三个点中的任何一个。
3. 这里比2阶平面的情况要复杂一些。 公理的陈述说，您需要至少找到一组（非空的）四个点，其中三个点都不能超过一条线。
   显然，图中的线通过的具有三个点的12组不满足此条件。 但这满足了例如四个角点的集合。

在更一般的情况下，阶数为n的有限仿射平面具有n ^ 2个点和n ^ 2 + n条线。 每行包含n个点，并且每个点都属于n + 1行。 [1]

仿射几何完成后，我们传递到平面上的第二种几何类型-射影。

相反，在投影几何中，任何两条线在唯一可能的点相交，因此不存在平行线。 [1]

前面的句子描述了射影几何的第二个公理。 第一和第三与雅典相同。

由于第三个公理要求至少存在四个点，因此平面必须包含至少7个点才能满足前两个公理的条件。 在最简单的投影平面中，也有7条线； 每个点属于三条线，每条线包含三个点。 这种投射平面通常被称为“范平面” 。 [1]

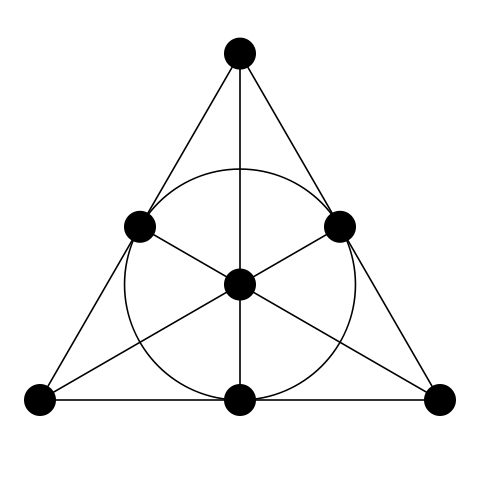
图 8.法诺飞机。 （来源en.wikipedia.org ）

在此图中，很难立即理解所有7行，因此这是同一平面的小马版本：

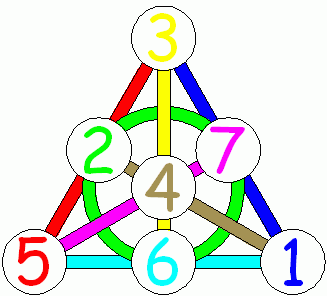
图 9.法诺飞机上有彩色线条。 （来源mathpuzzle.com 。经Ed Pegg Jr.允许使用。 ）

因此，法诺平面是具有7个点和7条线的2阶投影平面。

该卡与它有什么关系？

如果我们重新制定两个有限几何公理，将“线”替换为“符号”，将“点”替换为“卡”，会发生什么？

结果是这样的：

1. 对于两个不同的卡，只有一个符号，这两个卡上均显示。
2. 对于两个不同的符号，只有一张包含这两个符号的卡。

现在，基于此知识，让我们看看在最简单的情况下Dobble的外观。 它有7张卡片和7个字符，每张卡片将有3个字符（因为3行在一点处相交）：

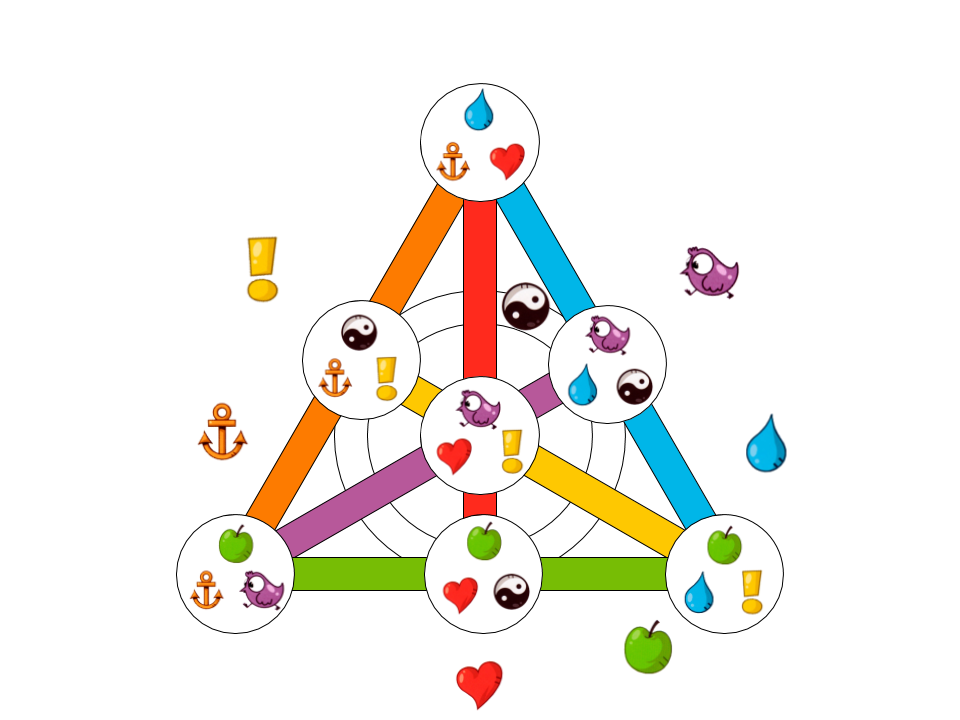
图 10. Dobble最小可能卡片集的示例。

这里使用以下7个字符：

， ， ， ， ， ，
无论我们拿什么两张牌，它们都会有一个共同的符号，该符号会在两张牌所在的行旁显示。
例如，左下角的卡和右侧中间的卡具有共同的符号 。 它显示在该行的旁边。 。

小订单的投影飞机

在Wolfram上，您可以找到小订单投影平面的视觉演示： http : //demonstrations.wolfram.com/ProjectivePlanesOfLowOrder/
它被设计为CDF格式（可计算文档格式）的文档，您需要为此安装CDF Player 。

这是一个三阶投影平面的示例：

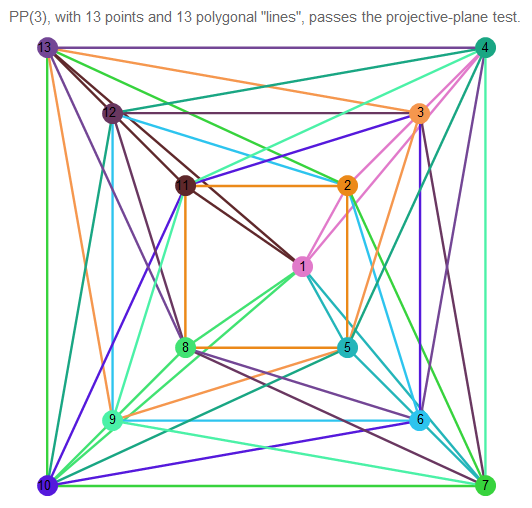
图 11. 3阶投影平面的图像。

很难理解正在发生的事情，因此请选择2行：

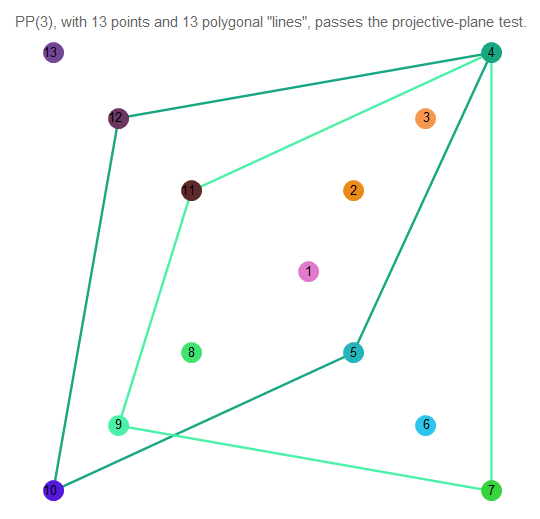
图 12.三阶投影平面的两条线的交点。

如我们所见，它们恰好在一个点处相交。 直线本身包含4个点。

为确保每个点有4条线，您必须在交互式文档中切换显示的线对并集中在某个点上。

下图显示了高阶的投影平面。

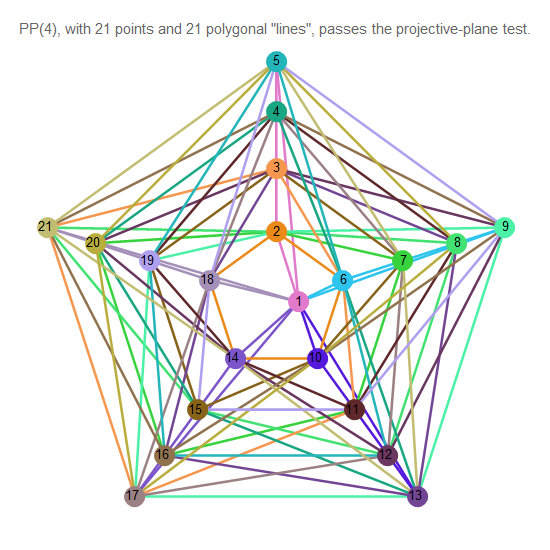
图 13. 4阶投影平面

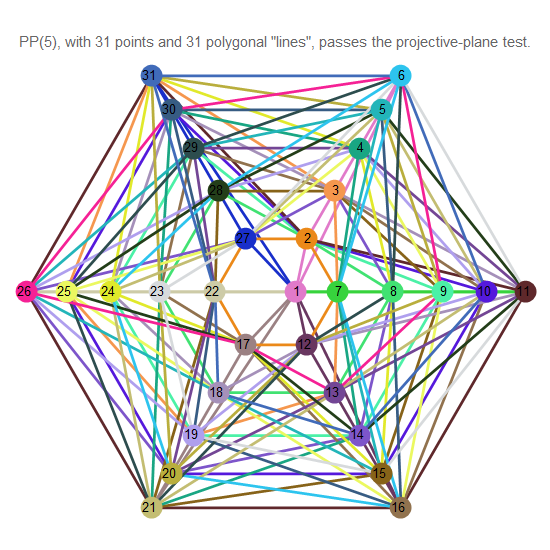
图 14. 5阶投影平面

图 15. 7阶投影平面

在上述序列中，没有用于6阶投影平面的图像。 这不是一个错误。

尽管Wolfram生成了这种结构的图形表示，但它不满足射影几何的公理，也不是射影平面。

假定但尚未证明，有限平面的阶始终是素幂 。 [1]

如何建造投影飞机？

投影平面的图形表示看起来有趣而清晰，但是如何找到这样的点组合以使其具有上述特性呢？

最简单的方法是访问托管了各种阶数的投影平面的预先计算数据的站点。

例如，对于第7阶的投影平面，您可以访问以下页面： https : //web.archive.org/web/20170619110638/https : //www.uwyo.edu/moorhouse/pub/planes/pg27.txt
此处显示数字矩阵。 线是就Dobble而言的卡片（点）。 行中的数字是从零开始的字符（行）的序列号，这些序列号绘制在每张卡上（通过此点）。

您还可以使用数学软件包（例如Matlab）的服务来构建投影平面的入射矩阵。 [2] [3]

发病率矩阵

入射矩阵是表示图形的入射元素（边（弧）和顶点）之间关系的图形表示形式之一。 矩阵的列对应于边，行对应于顶点。 矩阵单元中的非零值表示顶点和边缘之间的关系（其入射角 ）。 [2]

入射矩阵的最简单示例之一可以是2x1矩阵，用于由一条边连接的两个顶点的无向图：

图 16.由一条边连接的两个顶点的无向图及其入射矩阵。

图及其关联矩阵的更复杂示例：

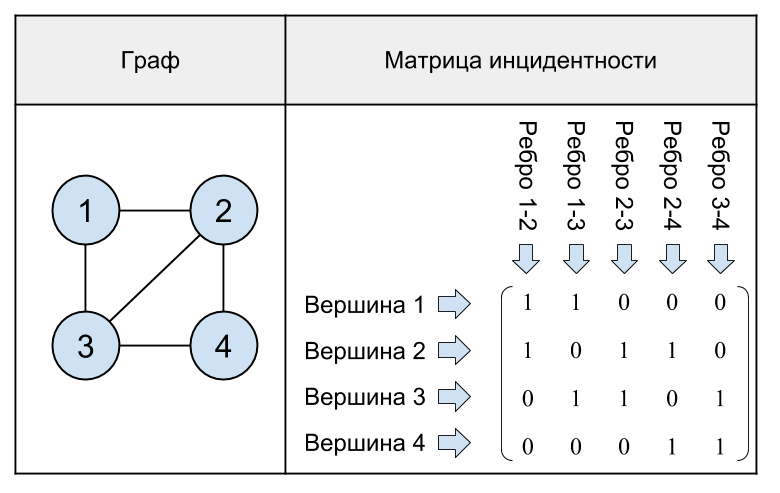
图 17.具有4个顶点的无向图及其入射矩阵。

从最后一个示例可以看出，在每一列的图形的关联矩阵中，正好有两个单位，因为 一条边连接两个顶点。
投影平面是一个超图 ，因为一条线（边缘）连接了多个点（顶点）。 因此，在投影平面的入射矩阵中，每列中的单位出现n +1次，其中n是投影平面的阶数。

对于图所示的Fano平面， 9，发生率矩阵如下：

图 18. Fano平面的入射矩阵。

为了简化感知，未显示零，并且用符号X代替单位。
在投影平面的这种表示形式中，点和线的对偶原理清晰可见-线正好穿过3个点，同时，该点正好属于3条线。

用蛮力建造射影飞机

关于入射矩阵性质的当前知识足以将其构造为任何n阶的投影平面。 为此，您可以使用以下伪代码：

          n+1 ,          n+1 ,                                ,                

按照此算法，我们获得Fano平面的对称矩阵 ：

图 19.由伪代码算法构造的法诺平面入射矩阵。

该矩阵与前一个矩阵不匹配。 实际上，没关系。
入射矩阵的任何两行的排列等效于对图的顶点重新编号。
入射矩阵的任意两列的置换等效于对图的边缘进行重新编号（如果它们已预先编号）。

Dobble的事件矩阵

对于在关联矩阵中的Dobble游戏，行负责卡片，列负责卡片上的字符。
因此，入射矩阵的任何两列的排列等效于卡片上字符序列的变化。 但是，卡上的符号是无序的，因此此操作不会影响卡的外观。
两行的重新排列意味着在所有卡上，两个对应的符号相互替换。

最后的操作会更改纸牌的外观，这意味着我们在游戏中看到的一组字符只是可能的组合之一。
给定卡的字符集数量是57个元素和8个元素的组合，没有重复。 由公式计算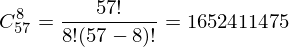

下表显示了Dobble的入射矩阵。 它是转置的 行是符号，列是卡片（图片可单击）。 Habr不允许您插入所需大小和质量的图片，因此完整大小选项是一个单独的链接： https : //github.com/Skybladev2/DobbleMathModel/blob/master/images/Dobble%20incidence%20matrix.png

图 20.游戏Dobble的关联矩阵。

游戏中缺少哪两张牌？

总计，带有游戏发生率矩阵的表具有57行55列。 这意味着游戏可以再有2张牌。
这意味着这些卡片上的角色在游戏中要比其他角色少见。 表格的最后一栏显示了游戏中的角色数量。

丢失的卡片中的字符数如下：

• ， ， ， ， ， ， ， ， ， ， ， ， 和
  （共14个字符）出现7次。
• 发生6次。

丢失的卡片是什么样的？ 要回答此问题，请在关联矩阵中（除雪人外）取上述任何字符，然后将其放在丢失的卡片上（例如，倒数第二列）。

然后我们找到在其上描绘了该符号的所有卡（列）。 这意味着在所有这些卡上，符号都重合，并且没有其他匹配项。

由于这些卡已经与所选字符匹配，因此从倒数第二列中删除出现在其他卡上的所有字符。
尚未删除的缺少字符，并构成剩余卡之一的字符。 由于事实证明它们恰好是8，因此可以明确确定第二张遗失卡的类型。

这是这两个卡：

图 21.可能的失卡类型为56号和57号。

还有一个问题要回答-缺少这些卡是否会影响两个卡之间单个符号的重合性（即突然之间某些卡之间没有匹配项）？

如果您仍然看一下游戏的发生率矩阵，答案是显而易见的-不，不是。 在任何两张卡（列）之间仍然是唯一的巧合。

为什么有2张牌比游戏中的最大张数少？

最初，这五款迷你游戏的规则不在小册子中，而是在五张单独的卡片上。 同时，只能打印60张卡。 因此，游戏的作者决定删除2张卡，最终结果是55张带符号的卡+ 5张带规则的卡。 （特别感谢Guillaume Gille-Naves的澄清。）

致谢

我感谢棋牌游戏商店“ Igroved”的网络为他们撰写本文提供的帮助。
感谢Ed Pegg Jr提供了Fano平面图像。
另外，我想提及一位匿名者和Master来帮助检查本文。
我感谢“ Table City”商店在准备文章发表方面的帮助。
我全心全意感谢游戏Igor Polouchine，Denis Blanchot，Guillaume Gille-Naves和Asmodee的作者拥有使用游戏图像的权利。