平衡三元
我正在为我们的大学从事计算机体系结构原理讲座; 作为一项作业,我想建议我的学生建造一个简单的
三元工作的可编程机器。 主要原因是很有趣:作为一名讲师,我必须带些娱乐性,否则我听不到。 此外,由于历史原因,这一点很重要。 还有什么“为什么?!” 将回答问题“因为我可以。”
该页面描述了非常基本的内容,不会超出简单的三进制加法器(及其硬件实现)。 敬请期待更多。
我选择了平衡三元系统:每个trit代表-1、0或1这三种可能的状态之一。在
这里可以找到对该系统的非常详尽的描述。

基本组成部分:三元复用器
抽象化
我的计算机中将使用的唯一块是三进制多路复用器。
可以将其视为具有五个引脚的黑匣子:选择器引脚接收三进制信号(-1、0或1),然后在盒子内部有一个小开关,将输出引脚与三个输入引脚之一连接起来inN,inO或inP。
通常将其描述如下:
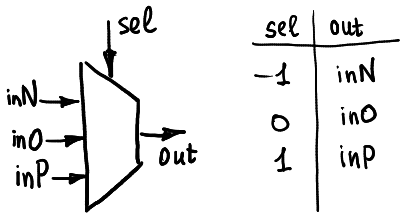
三元解复用器的工作方式类似:根据选择器引脚,一个输入与三个可能的输出引脚之一连接。 请注意,在我的硬件中,我使用CMOS模拟开关。 它们是双向的,因此硬件既可以用作复用器,也可以用作解复用器。 但是无论如何,目前我不使用解复用的可能性。
硬件实施
基本设计由
Shaos提出。
我所做的唯一一件事就是创建SRIM版本的TRIMUX。 表面贴装dg403开关在中国的每片价格为50p。
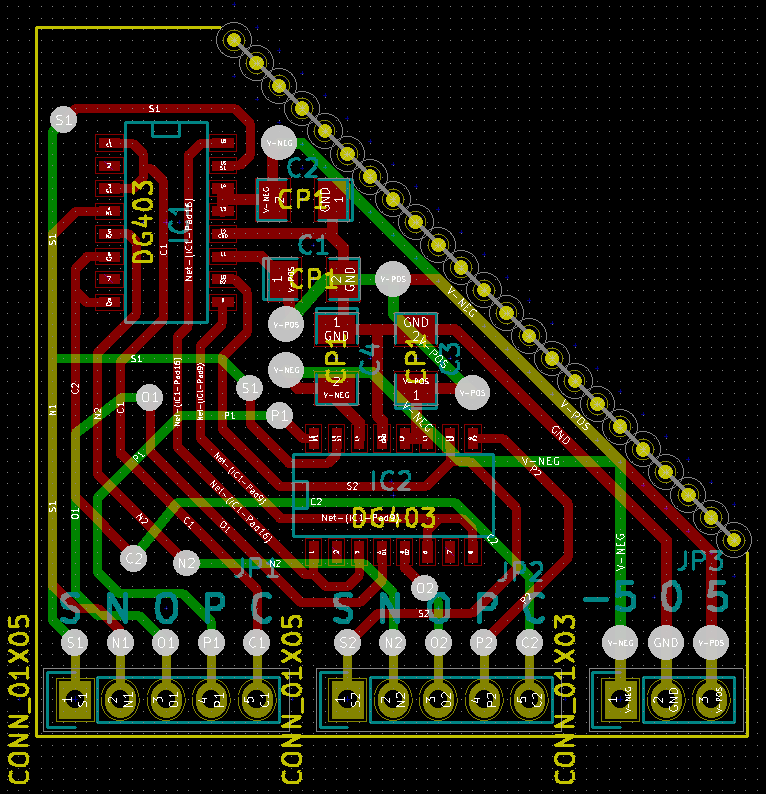
在找到这种设计之前,我曾尝试使用cd4007和cd4016的组合。 它可以工作,但是硬件笨重且难看。 DG403交换机提供了真正的三元计算可能性,没有任何冗余,例如使用两位二进制和禁止四种配置之一。
可以使用两个DG403创建一个三元多路复用器:其中一个IC接收-5V至0V电源输入,而另一个IC用0V至5V供电,并且它允许使用由三个电压-5V,0V和5V表示的三元信号,分别。 此设计仅使用dg403引脚的一半,因此很自然地创建一个带有两个多路复用器的电路板。
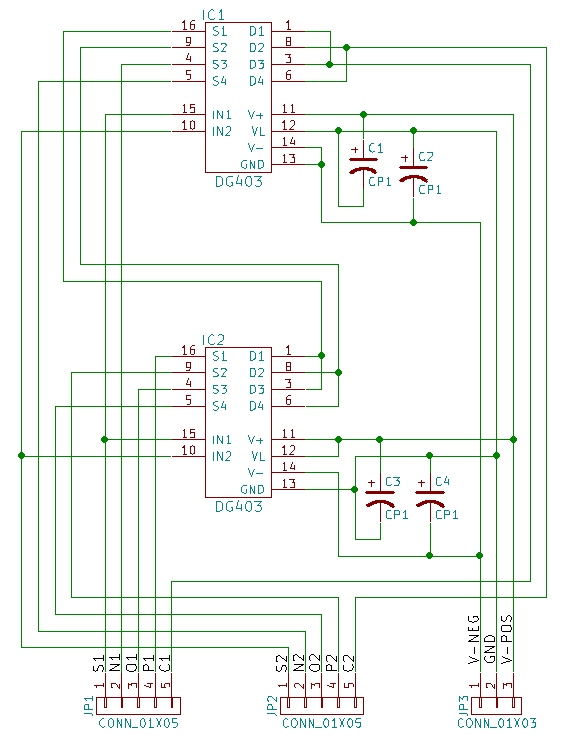
请不要
在这里与Shaos联系。 令人惊讶的是,他没有猜测三元的好处,而是设计和制造了自己的三元IC!

如何使用? 一元函数
让我们省略通过将-1.0和1赋给多路复用器的相应输入引脚可获得的标识函数。
首先,让我们通过计算A +1(当然,在-1,0,1环中)来递增输入信号A:
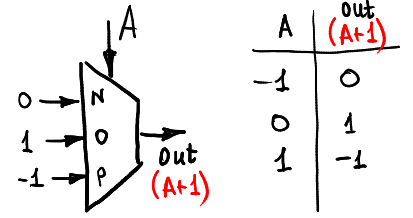
这是我们减少输入的方法:
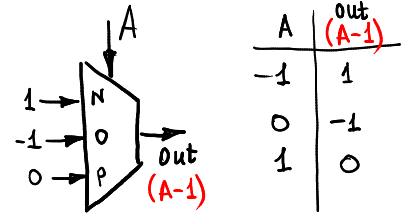
让我们计算最大值(A,0):
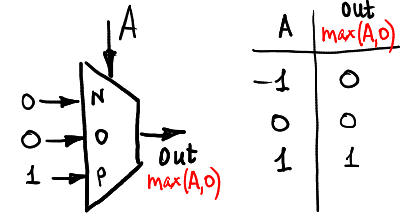
最小值(A,0):
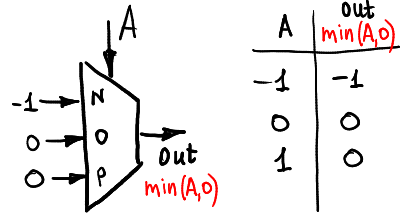
两个参数的功能:半加法器
A + B
因此,一个多路复用器允许我们计算任何一元函数。 要计算两个自变量的函数,我们需要使用三个或四个多路复用器。 例如,如果我们要计算两个信号A和B的总和(仍在环-1,0,1中),则可以使用以下模式:
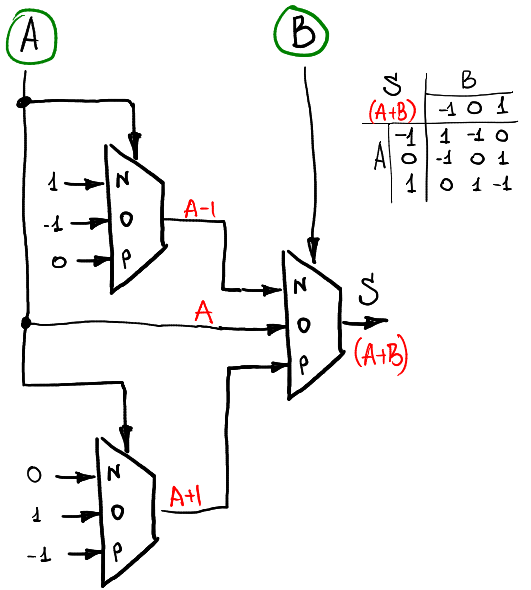
多路复用器有两层:第一层计算A的一元函数,第二层根据B组合它们。
共识
如果我们要计算两个三元信号的共识函数(如果A = B = -1,共识等于-1,如果A = B = 1则共识等于1,否则为零),则可以这样进行:
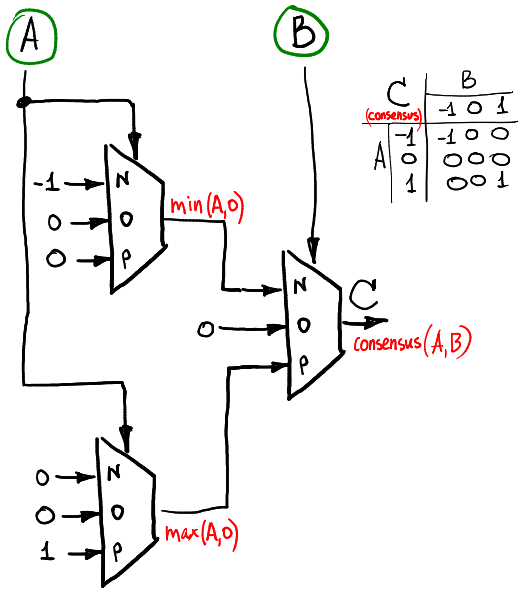
硬件实施
实际上,我们只是创建
了一个半加器 。 对于两个输入A和B,它计算两个输出S和C,它们的关系为A + B = S + 3 *C。 S是总和,C是进位标志。
让我们测试设计! 红色LED表示-1,熄灭表示0,绿色LED表示1。因此,这张照片告诉我们S = -1,C = 1,或者换句话说,1 +1 = -1 + 3 * 1:

下表列出了半加法器的所有九种可能状态。 每个单元格都提供S和C的对应值。为每个单元格提供指向照片的链接。
三个参数:完全加法器
与半加法器相反,
全加器接收三个输入A,B,Cin,并计算两个输出S和Cout,它们分别与A + B + Cin = S + 3 * Cout有关。
三重合计
如果要计算A + B + Cin的总和,则想法与以前相同:我们使用输入的逐层准备。 第一层使用A作为输入,第二层使用B,最后一个单路复用器层使用Cin。 这是一种计算输出S的可能方法:
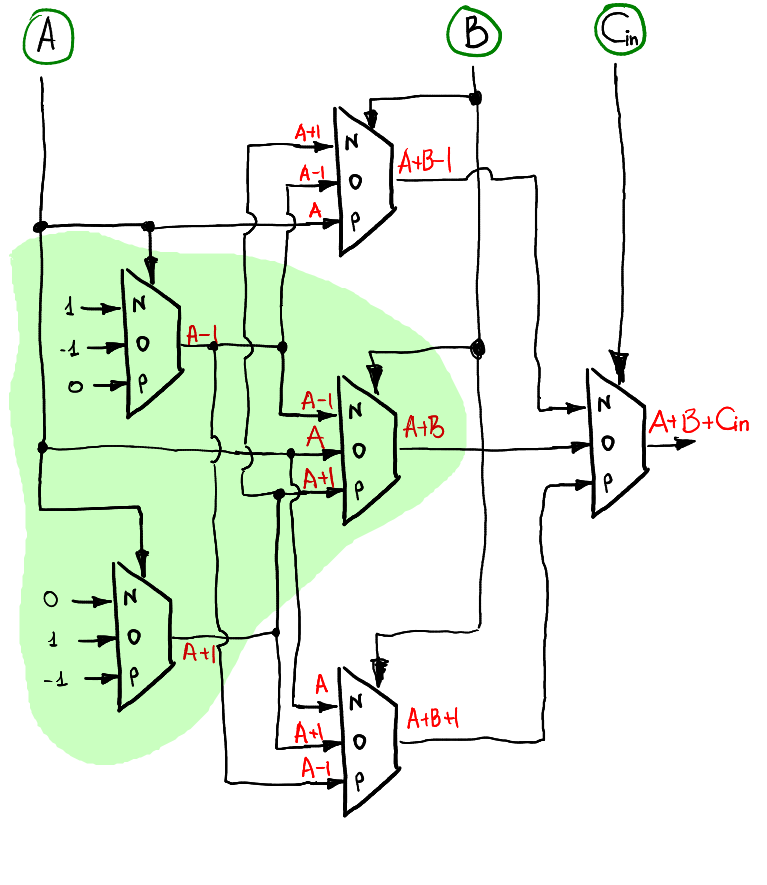
请注意,当Cin = 0时,它的行为与半加法器完全相同,因此很自然地看到半加法器原理图包含在全加法器中(以绿色突出显示)。
溢出(进位标志)
溢出三态可以以相同的逐层方式计算。 它还包括半加法器!
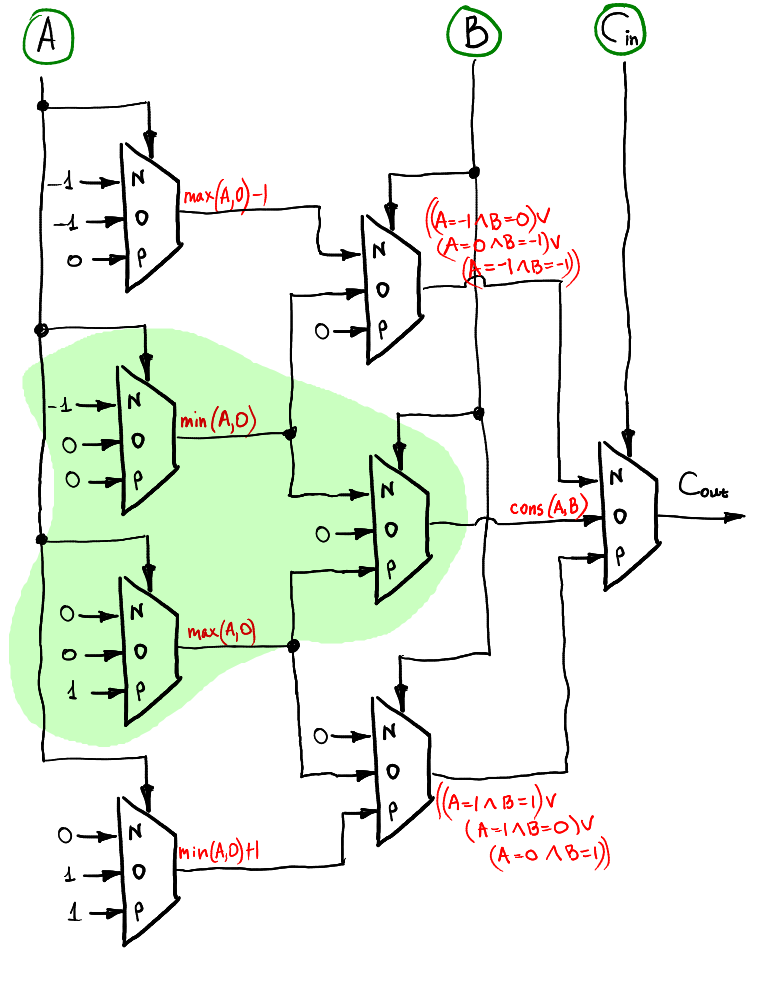
硬件验证
这次我懒得用面包板测试完整的加法器,所以我制作了这层PCB:

蚀刻铜之后:

以下三个表格列出了全加器的所有27种可能状态。 和以前一样,每个州都可以使用这些照片。 请注意,中间表(Cin = 0)与半加器完全相同。
相对于半加法器,全加法器的优势在于可以堆叠多个加法器,直到获得足够的三叉戟表示所需的数字为止。
这是两个加法器的堆栈:

这里是它如何解决-4 + 2(最不重要的Trit在左边):

当然,最低有效三叉戟不需要完整的加法器板(最低有效三叉戟的输入没有进位标志),半加法器就足够了。
结论
这是三元计算入门的结尾。 请继续关注时钟,计数器,内存等等!