轻松自做物流

我想与您分享在一家贸易公司中创建物流系统的经验。

美好的一天，在2012年左右，负责人设定了任务：考虑优化组织运输物流成本的问题。
企业的主要活动领域是产品的批发和交付，其中运输成本占据了很大一部分成本。

管理层认为，现在该是时候整顿事情了，以花钱买燃料，而且还有人怀疑驾驶员还参与了两次航班之间的“左手”交付。 在中小型企业中，很多是建立在信任之上的，因为保持个人的控制权是无利可图的，并非总是明智的。 当成本上升而效率下降时，您只需要做一些事情即可。

首先，我们尝试通过管理方法解决该问题：连续测量油位，转速表读数，在货物个人陪伴下测量交货时间。 效果只不过是消极，怀疑和不必要的动作（测量对于某人来说也是一项工作）。 如果仍然可以通过一条路线确定一个大致范围，那么通过25-35个零售设施的飞行，一切都会发生很大的变化，时间和燃料上的差异很大。

目标：将繁忙的车辆送往贸易企业，减少里程，从而降低成本。 如果可能，请避免偏离路线。 昨天可以这么说，目标是通过最少的财务和实施时间投资来降低成本。 在讨论中，他们商定了几种替代方案：

1. 使用其中一项服务来计算路线并核算燃料和润滑油；
2. 配备车队跟踪/跟踪模块；
3. 自己设计一些东西；

我们决定尝试所有三种解决方案并选择最佳解决方案：

1.当时，我们没有找到一个好的交钥匙解决方案。 既可以使用交钥匙设计，也可以使用昂贵的产品，也可以按原样并经协议进一步使用。 尝试了几种在线服务。 总的来说，这还不错，但是基本上困难在于从会计系统中复制信息，获得结果的操作次数（单击此处，转到此处，更新目录），所有内容都在线（在当时很关键）。 但是最大的缺点是难以创建具有许多点的路线并选择最佳路线。 通常，必须手动选择所有内容，并调整值，这很长，因此并不总是成功。

经过几个月的工作，他们拒绝了这个决定。

2.作为一项实验，他们在十几辆汽车上安装了GSM跟踪模块。
结果更加成功。 您总是知道汽车在哪里。 但是成本比第一种选择昂贵。 但是，在确定了几条偏离路线的情况（一名司机安息日，第二名司机在工作时间内拜访心脏女士）后，工作人员开始集中精力清除此类设备。 尽管他们以前没有热情地接受过这项创新。 电源端子意外闪烁，或者维修发动机时，设备出现故障，或者电子设备在阳光下“过热”。 因此三年来，我们丢失了9台设备。 总的来说，这个决定是积极的，但是有一个缺点-我不得不看很长时间的路线来确定可疑活动，这不是很方便。 跟踪系统中的一个加号是导出跟踪的项，它允许累积某些路线统计信息。

后来，我们使用了一家主要移动运营商中的另一套系统进行公司通讯并跟踪销售代理商的活动，结果是相似的：SIM卡坏了，电话丢了，他们在家里被遗忘了，电池电量耗尽了，人们总会找到出路。

3.与前两种方法并行，我们决定发明一种自行车 ，以在我们的会计系统中实现自行构建路线的能力。

首先，我们带来了所有的参观地点，并将其地理坐标输入数据库。 我们在访问时根据GPS跟踪器获取坐标，也可以从OSM地图中直观地获取坐标，然后使用鼠标找到正确的位置并复制坐标。

在第二阶段，必须以方便的格式获取该区域的矢量地图。
选择是在同一OSM上，因为这些卡具有开放格式。 我们没有掌握地球的转储信息，因此我们首先通过OSM本身的导出，以XML的形式将数据分段上传，然后连接区域。 后来遇到了一个GIS-LAB项目。 多年来，这些有价值的人每天都在按地区划分垃圾场 。 但是每个人都想吃，项目最近停滞了，伙计们搬家了 ，他们以合理的价格做着同样的工作。

收到XML格式的地图后，我们根据规范提取了负责道路的图层。 由于几个相邻区域的卡容量占用了10 GB，因此SAX解析器是用RUBY编写的，它仅选择必要的标签并合并了在单个结构中进行活动的相邻区域。

项目本身是作为外部DLL编写的，以Pascal编写的会计系统。 可以说，该系统可以运行的设备数量已过时，因此RAM的限制为1 GB（是的，也有使用该技术的公司已经使用了10年，并且将以相同的数量工作）。 最初，人们希望将卡分解成块，然后根据需要将其加载到RAM中（例如在导航器上），但是速度非常慢。 结果，我们设法组成了合理的50 MB。

在OSM中，道路图表示为具有附加属性的道路矢量部分。 在我们的决定中，我们使用了邻接表 。 峰是地图上的一个点，边缘是到相邻点的路径。 对于优化，我们认为从一个顶点最多可以有四个路径（相交）。 如果路径多于4条，则需要将边分成两个附加的边，因此对于每个地图点，我们总是有固定数量的边=4。虽然有些冗余，但这种方法允许我们对齐内存中的数据。

值得注意的是，地球不是一个球（出乎意料的），而是一个大地水准面 ，但出于制图的目的，它被简化为椭球形或椭球形 。

出于我们的目的，我找到了一个公式来计算椭球表面上两点之间的距离，虽然我无法理解其最深层的含义，但这并不妨碍我们使用它。


创建路基后，需要一个可视层来显示周围区域。 映射项目在这里起到了帮助作用，它使我们能够通过近似层将区域的OSM地图解析为图块部分，就像10 ^ 100或Yandex。 曾经尝试过在线处理巨人地图，在浏览器层的顶部绘制矢量地图，但是由于许可限制，他们决定拒绝。 结果，我们创建了一个虚拟磁盘，并将图块的转储上传到那里的几十个千兆字节，但是一切都在眼前，并且不会减慢速度。 是的，大约每六个月必须刷新一次，通常这与存储卡过载有关。



要组合图块图像和矢量地图，您需要知道图块，Google，OpenStreetMap，Bing和Yahoo在Mercator投影中表示（更确切地说是WEB MERCATOR ，这是到球体上的投影），其中每个更深的层比上一个图层的详细度高两倍。



Yandex.Maps使用墨卡托椭圆体的投影。

是否可以重新计算投影平面上的地理坐标，反之亦然。

我们选择了细节级别17作为最大级别。 由于磁贴数量（每个级别比上一个大4倍）的存储量的增加，以及它们的信息含量低，更接近没有意义。

2 ^ 17 * 256 = 33554432（256是图块边缘的大小，以像素为单位）。


现在我们有了基本工具，我们可以直接进行创建最佳路线的任务。 我们将购物设施与路线图中最近的边连接起来，然后开始搜索最短路径。 为此，我们对每个访问点依次使用Dijkstra算法的一种变体，以解决其放电变化。 在输出中，我们得到大小为（N + 1）*（N + 1）的邻接矩阵，在主对角线上（无障碍），其中N是访问点数，而没有考虑出口点。

所得矩阵存储所有购物设施之间沿道路的最小距离，这是一个经典的旅行推销员问题 。 由于此类问题的算法复杂度最高，因此我们使用了分支定界法来解决该问题。 对于n <15，它是详尽无遗的；否则，将进行深度估计。 该选项当然不是理想的，但是相当有效。

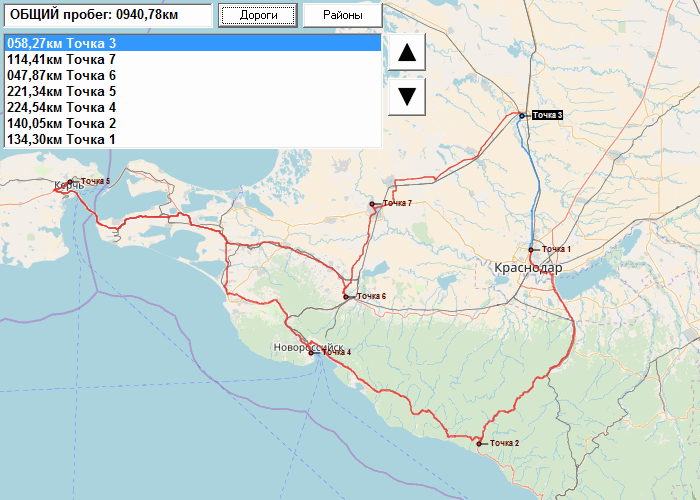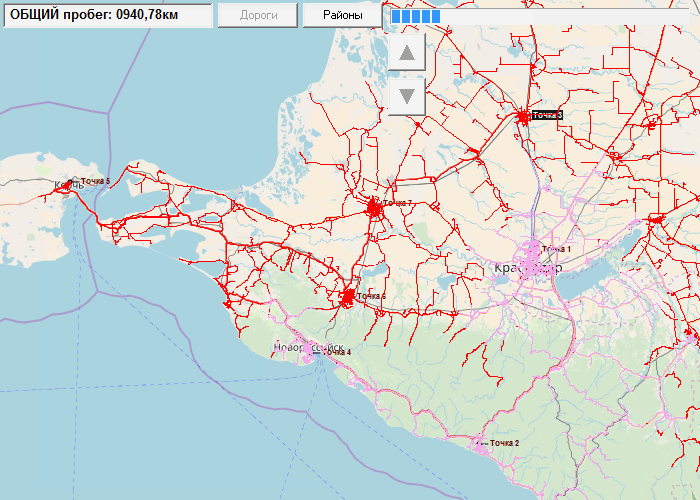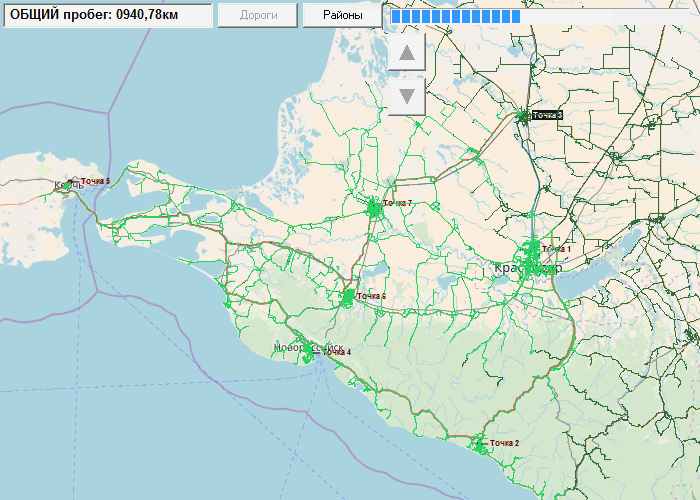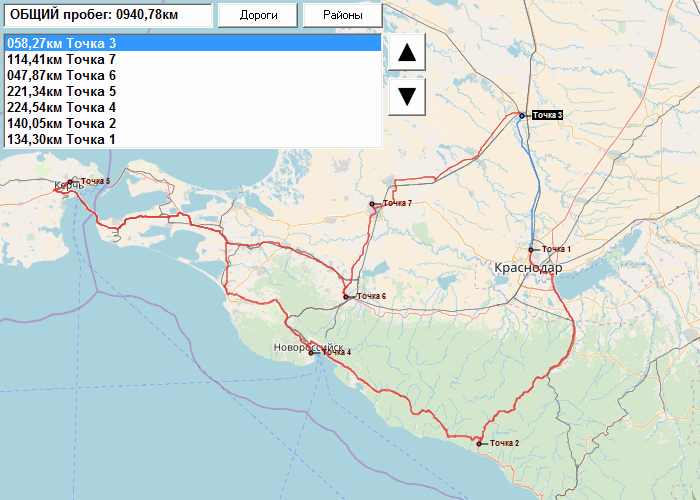
结果，我们得到的路线接近最佳距离，以公里为单位。 如有必要，操作员可以根据各个点的优先级手动更改路线。

该解决方案已经在组织中工作了大约7年，尽管在准确性和便利性方面都没有缺陷，但已经相当成功。 结果与GPS车辆跟踪数据一致。 据我估计，物流的引入可以节省燃料分配资金的10-12％。 该程序仅由一个人（您的谦卑的仆人）设计，启动和陪同。

我保守的领导层并不渴望“发光”，因此我提出了一个虚构的例子来说明关注的途径。



没有可视化，计算速度几乎快一倍，而且几乎可以立即完成一次结算。

这么多年之后，有时会不停地尝试进入代码并将其以新的经验复制到新的，更现代的平台上，但是到目前为止，这在经济上是不可行的。

我只想告诉您，我希望这很有趣。
如果我在某处不准确，我深表歉意。