我们大多数人的日常行程仅限于从家到公司上下班。 阻碍我们前进的最困难的障碍是交通拥堵。 但是在我们国家,有很多地方只能乘专用车。
如果您不需要定期搬运大量货物或前往这些人迹罕至的地区,则这种运输是不错的选择。 然后,我们应该已经考虑过建设基础设施,可以在通常的民用运输工具上进行移动。
如果设计一条未来路线的整个复杂性在于找到一把尺子和一支铅笔在地图上绘制连接两个对象的直线,那将是一件好事。 但是,a,我们的现实与此截然不同。 如果上方的地形像一块瑞士奶酪一样好怎么办?

一年多来,我们一直与数字设计研究实验室的同事合作,开发出一种可以自动模式构建各种通信网络的工具。 有关详细信息,欢迎猫。
一切如何开始
通常,到这样偏远的地方旅行是由于某些经济利益。 而且,尽管人们通常事先知道这些领域的发展会带来丰厚的利润,但为什么不省钱就可以在没有特殊困难的情况下完成工作呢? 如果设计得更胜任的路线使我们不必再多加建几公里的高速公路怎么办?
但是,仅道路的可利用性获得任何可观的利润显然是不够的。 基本上,它仅由矿藏带来。 因此,除了道路之外,还必须设计各种管道网络,自来水管道网络,带有正确放置的变电站的电力线网络。 所有这些基础结构都可以指定为线性对象。

当工程师面临着在复杂的工程和地质条件下在地面上设计通信网络的任务时,他的工作就变得异常复杂。
如何不进入河水泛滥区? 如何最小化多年冻土的路径? 通过沼泽铺设道路时如何节省沙垫? 哪里可以买到这个枕头的沙子?
这只是工程师在工作中问自己的问题的一小部分,但是您仍然需要考虑各种GOST和SNiP。 好吧,如果您仅想连接两个对象,并且是否有几十个对象?
因此,设计行业急需一种工具,该工具既可以计算工程师设计的线性对象的成本,也可以计算以自动模式构建线性对象的能力。
资料
开始任务时,我们必须处理的第一件事是数据搜索。 需要什么数据? 在哪里买? 如果第二个问题可以在用户的帮助下解决,那么要理解第一个问题,我们需要认真的分析。
正确计算所需的数据确实非常多-从最平庸的标记湖泊和河流的区域,各种沼泽以及喀斯特地区开始,强烈建议不要在其上建造,以免造成倒塌的威胁。 因此,除了可以从卫星看到的区域外,这里还需要该区域的地质研究数据。
但并非所有数据都限于我们国家的自然物体。 还有很多人创造的东西。 例如,在道路建设中,我们可以使用之前建造的道路。 但是,在管道建设中,使用现有基础设施的可能性远非总是可能的。 由于新管道与现有网络的连接可能无法通过水力计算。
除了重复使用以前由人创造的东西外,还必须考虑到对任何物体附近构造的各种限制。例如,对于电力线的构造,您需要根据电力线本身的电压考虑人类居住地的凹痕。
但是,仅在平面上考虑问题的计算是不完全正确的,因为除了平坦的地形之外,还有海拔差异很大的区域,在这些区域上也无法进行施工。
与在区域标记和现有基础架构上获得数据相比,在地形上获得数据要简单得多。 为了简化开发,我们使用任何人都可以获得的开放式SRTM(航天飞机雷达地形任务)高程数据。

因此,我们有了数据,知道了我们可以在哪里建造,在哪里不能建造,以及地形不同区域的建造成本。 我们有一个区域,它具有要连接到单个通信网络中的一组对象。 用数学术语来说,这听起来像是在寻找解决斯坦纳问题的方法。
一点数学
众所周知,每个公式将读者数量减半,因此我们大大减少了本节的内容...
为了优化设计的线性设施的路线,必须能够计算其建造成本。 每个线性对象可以表示为多段线 L = \ {A_i,B_i \} _ {i = 0} ^ n 由段组成 。
每个直线段的建筑成本可以表示为一个功能值 ,其中每个段均通过参数指定:
$$ display $$ {\ displaystyle AB_i \ Colon \ left \ {{\ begin {aligned}&s = s \ left(t \ right)-\ mbox {parameterized curve},\\&h = h \ left(s(t )\右)-\ mbox {高程函数},\\&c = c \左(s(t)\右)-\ mbox {在某点的单位建筑成本函数},\\ \末端{对齐}} \右。} $$显示$$
在哪里
-段参数化。
在哪里 -不考虑浮雕的地球表面的公制张量,换句话说,就是测量地球表面距离的功能。
由于我们的行星具有大地水准面的形状,因此有必要使用特殊的公式来测量距离。 为此,我们使用Haversinus公式。 在其中,行星的形状看起来像一个球体,但这足以满足我们的目的,因为测量误差约为0.3% ,并且使用此方法计算距离的速度仍然很高。
寻找最佳方法的方法

但是在继续加入一组对象之前,您需要学习如何找到两者之间的最佳路径。 立即想到两种方法:
- 建立图表,然后应用最短路径搜索方法;
- 使用基于优化方法的解决方案。
在实现第一种方法时,我们遇到了与构造图以获得最大可能精度的方法有关的问题。 必须在图中的顶点和边的数量,解的质量以及计算时间之间找到平衡。
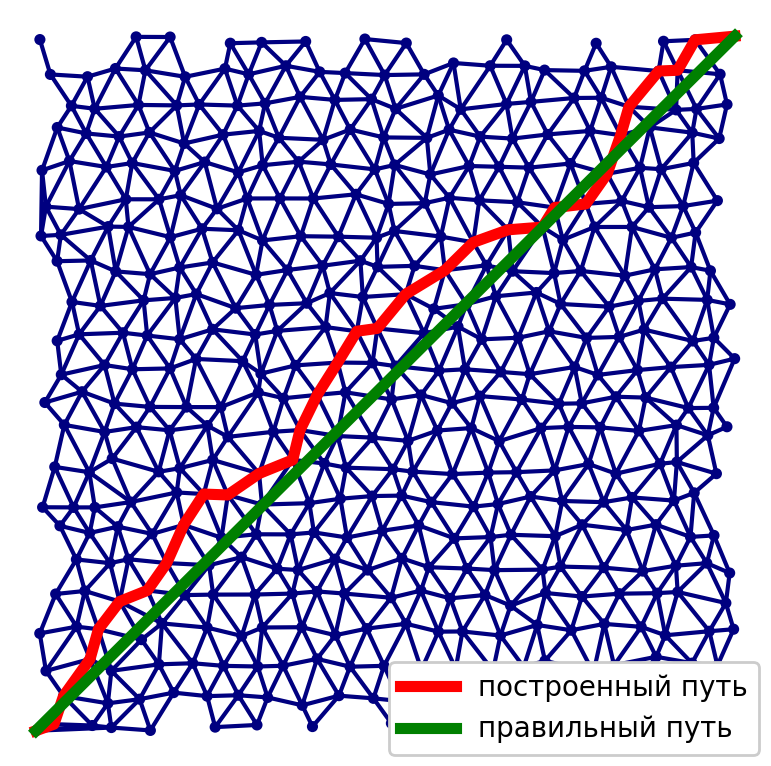
在第二种情况下,主要问题是局部极小值。 很容易选择解决方案可能无法收敛或远非最佳的情况。 由于通过这种方法获得的解非常依赖于初始近似。 如果我们有一个好的初始近似值,那么结果将是高质量的。
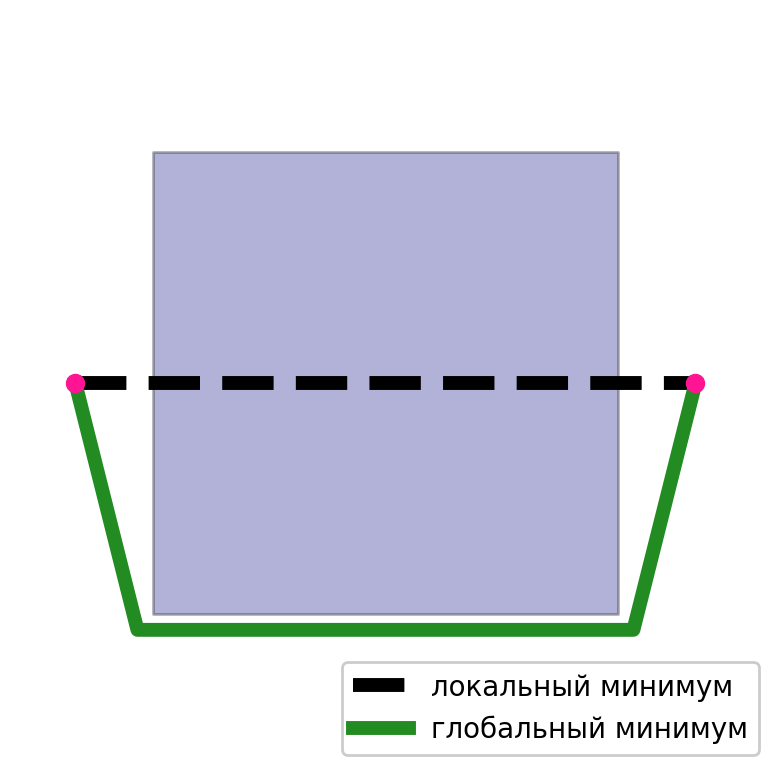
因此,我们有两种方法可以解决此问题。 第一个质量较低,但是没有局部最小值的问题。 第二个问题是局部极小值问题,但是是高质量的解决方案。 而且,如果您正确地结合了这两种方法,那么每种方法的缺点都会消失。 我们将在图上获得的解作为初始近似值,然后对其应用优化方法。
在本文的这一部分中,我们将在图形上准确考虑针对此问题的建议解决方案。
工具选择
行动计划已被概述,仅用于“编码”。 由于在编写应用程序的初始阶段,我们对主题领域知识不多,因此我们需要一种灵活的语言,以便在某些粗略的体系结构计算错误的情况下,我们可以重写几罐晚啤酒的全部代码。 我还可以选择在所有场合使用图书馆,以免诉诸自行车的发明。 因此,选择了Python作为主要的编程语言。
在应用程序中,我们使用了令人印象深刻的技术堆栈,该堆栈不限于以下内容:
- 匀称地处理诸如多边形和折线之类的几何数据;
- 几何熊猫工作方便匀称 ;
- scipy用于存储计算出的图并找到最短路径,以及找到最小生成树;
- PyTorch用于成本功能;
- 用于处理图像的枕头 。
实作
该模块可以分为几个阶段:
- 成本函数生成;
- 计算网格生成;
- 根据网格构建图;
- 图权重
- 图上最短路径的计算。
由于图形的边缘是段,因此我们可以通过计算某个积分的值来加权这些边缘,如上所示。 但是图中有很多边,因此,需要为大量点获取成本和高度值,这可能会花费很多时间。
最初的想法是通过确定一个点是否属于多边形来找到建筑的单位成本。 但是,由于此方法的算法复杂度高,因此注意到了这一想法,因为可以有很多多边形,并且每个多边形都有大量的顶点。
因此,为了解决这个问题,我们可以以图片的形式表示我们拥有的所有多边形,而这些多边形在数学上是一个矩阵。 因此,我们可以得到超过O(1)的点的单位建造成本,因此可以得到高精度建造特定肋的成本。
现在我们已经准备好构建图形,但是没有一种唯一正确的方法来构造它以获得高精度解决方案。 为了构造图形,必须生成计算网格,即所考虑区域中的一组点,这些网格以对应的顺序通过形成单元面的线段进行连接。 网格可以分为两种:均匀网格和不均匀网格。


统一网格模型描述了各个点的坐标,因此网格节点之间的距离是相同的。 不均匀的网格显示为单个点的随机集合。
使用均匀的网格并不一定总能找到找到最短路径的高质量结果,因此,有必要在不均匀的网格上测试这种方法。 最通用的是三角形网格。
通过将具有一定系数的噪声引入均匀的矩形网格中,然后对这组点应用Delaunay三角剖分点来生成网格。
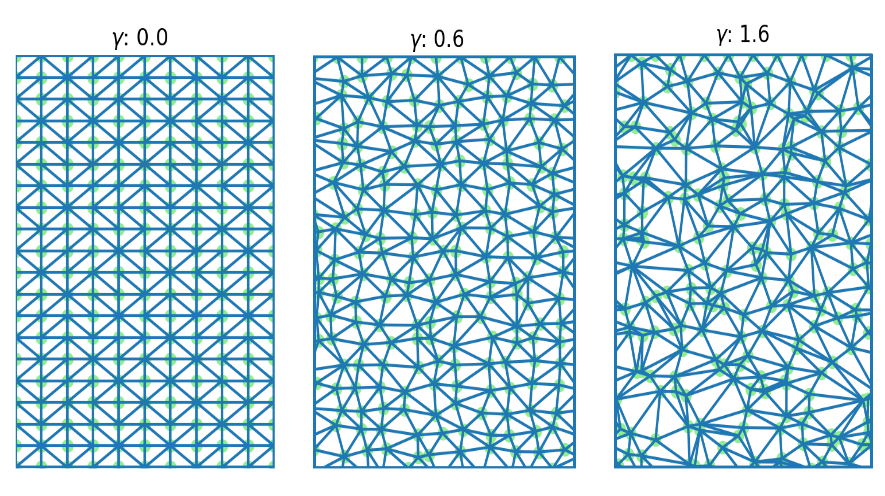
在该区域的各种模型图上测试了所构建网格的有效性,其中考虑了区域和浮雕的不同成本,然后与以解析方式获得的解决方案进行了比较。 通过搜索图边的长度和将噪声引入均匀网格的系数,找到了最佳参数以构造两点之间的最佳路径。
主要问题
最初,一切顺利,该算法计算出了最优网络,但是一旦构造路径的质量出现问题。 情况很简单:您必须在相当长的地图上连接两个对象。 该算法不想建立明显正确的路由。
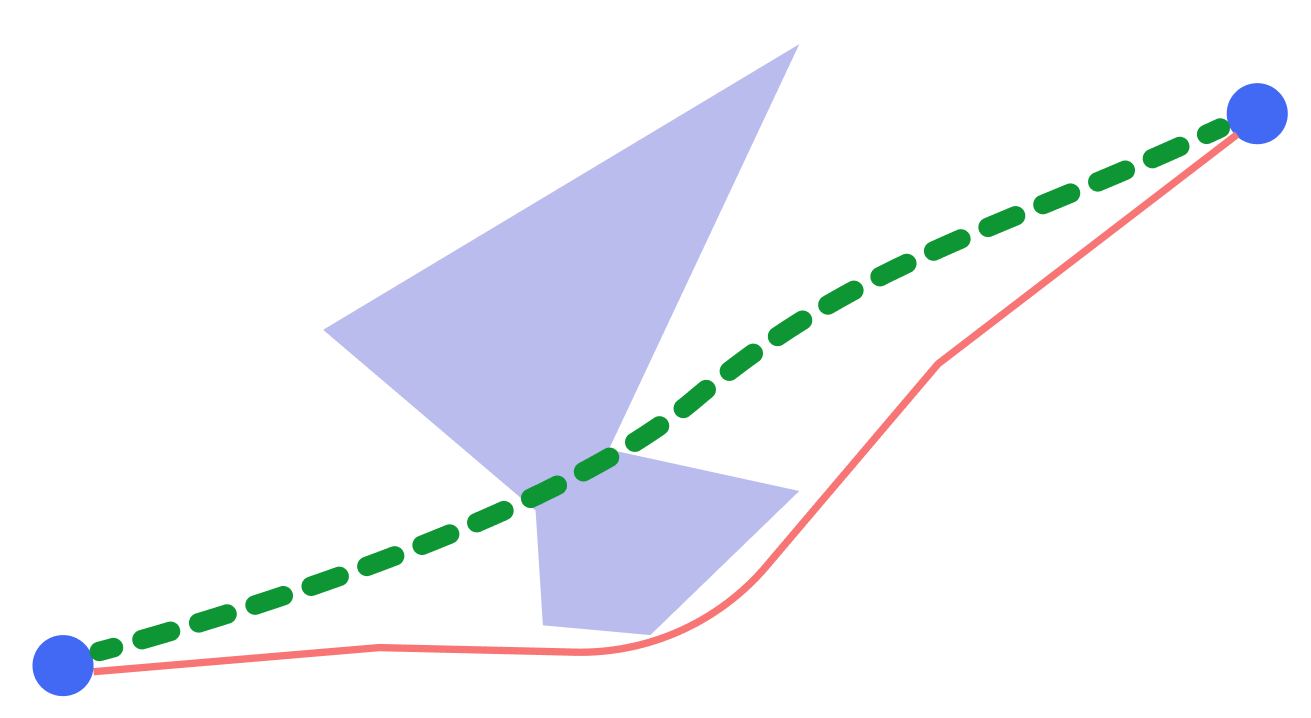
像往常一样,问题出在计算网格上。 我们通过网格的外观继续进行实验,得出的结论是,将顶点连接到图形(每个顶点都连接到n个最近邻居)是解决问题的方法。
联网
在学习了如何找到两点之间的最佳路径之后,下一步就是解决构建线性物体的最佳网络的问题。 文献中遇到的在图上构造Steiner树的算法是针对更一般的问题的,因此在我们的案例中将是无效的。 我们的图非常稀疏,相对于图中的顶点总数而言,终端顶点的数量很少,因此我们的任务也适用。 因此,由于许多其他原因,决定开发我们自己的算法,该算法使用某种启发式方法有效地构建最佳网络。
对于我们的案例,在图上构造最佳网络的算法的描述是单独出版物的主题,在此不再赘述。 由于在计算实际任务时,必须考虑到建筑行业中与最终用户相关的许多其他条件,这对所使用的算法施加了某些限制。
真实案例
因此,现在我们来看一下算法的结果。 我们的任务是将给定的一组对象与通信网络连接。 该算法的结果与以前建立的道路网络进行了比较。 现有网络的总长度为153.5公里,而计算得出的总长度为122.6公里。 这使道路网络的长度减少了25%,最终将节省大约5-15%的基本建设成本。
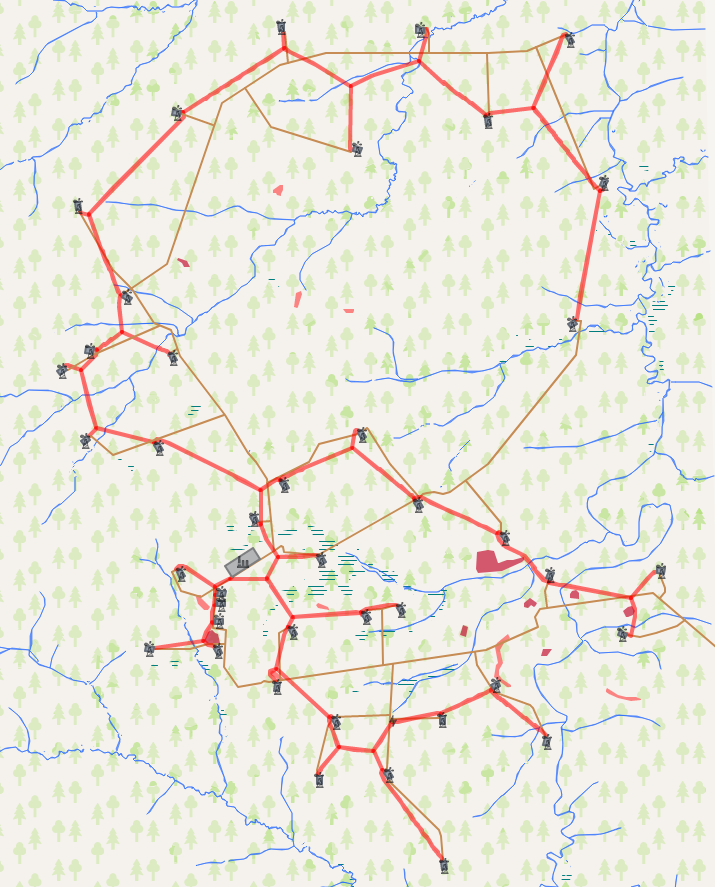
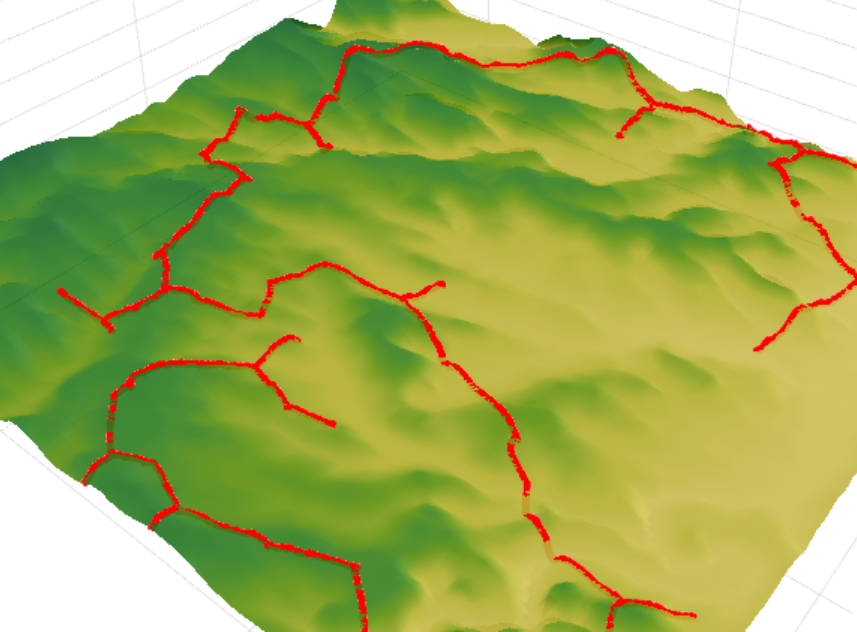
您可以在
此处更仔细地查看计算结果。
本文的下一部分将对使用的优化方法进行描述。