自动布局的数学基础

许多开发人员认为“自动布局”是一个难题，也是一个问题，对其进行调试非常困难。 如果根据我自己的经验得出这个结论是很好的，有时只是“我听说，我什至不愿与他交朋友”。

但是也许原因不在外面，而是在里面。 例如，食火动物世界上最危险的鸟类不会无缘无故地袭击人们，只是出于自卫。 因此，请尝试假设一秒钟，这对自动版式还不错，并且您对它的理解不够充分，也不知道如何烹饪。 这就是安东·谢尔盖耶夫（Anton Sergeyev）所做的，并深入研究了该理论，以便准确地理解所有内容。 我们对现成的Auto Layout的数学基础有所了解。




自动版式是一种版式系统 。 在深入研究之前，让我们先讨论一下现代排版。 然后让我们处理自动版式 -我们将弄清楚它可以解决什么任务以及如何完成它。 让我们考虑一下在iOS中实现自动版式的功能 ，并尝试开发实用的技巧以帮助您使用它。

这个故事将非常接近数学文章，因此我们首先要在表示法上达成一致，才能说出相同的语言。


关于演讲者： Anton Sergeev（ antonsergeev88 ）在Yandex.Mart团队工作，负责iOS上Maps的移动客户端。 在进行移动开发之前，他处理过电厂控制系统，在该系统中，代码错误的代价太高了，无法容忍。

名称

自从学校以来，我们就很熟悉线性方程组-用大括号表示它们，而它们的解决方案已经没有了。 同样，线性方程组的实体具有自动布局-限制。 它们由一条直线表示。



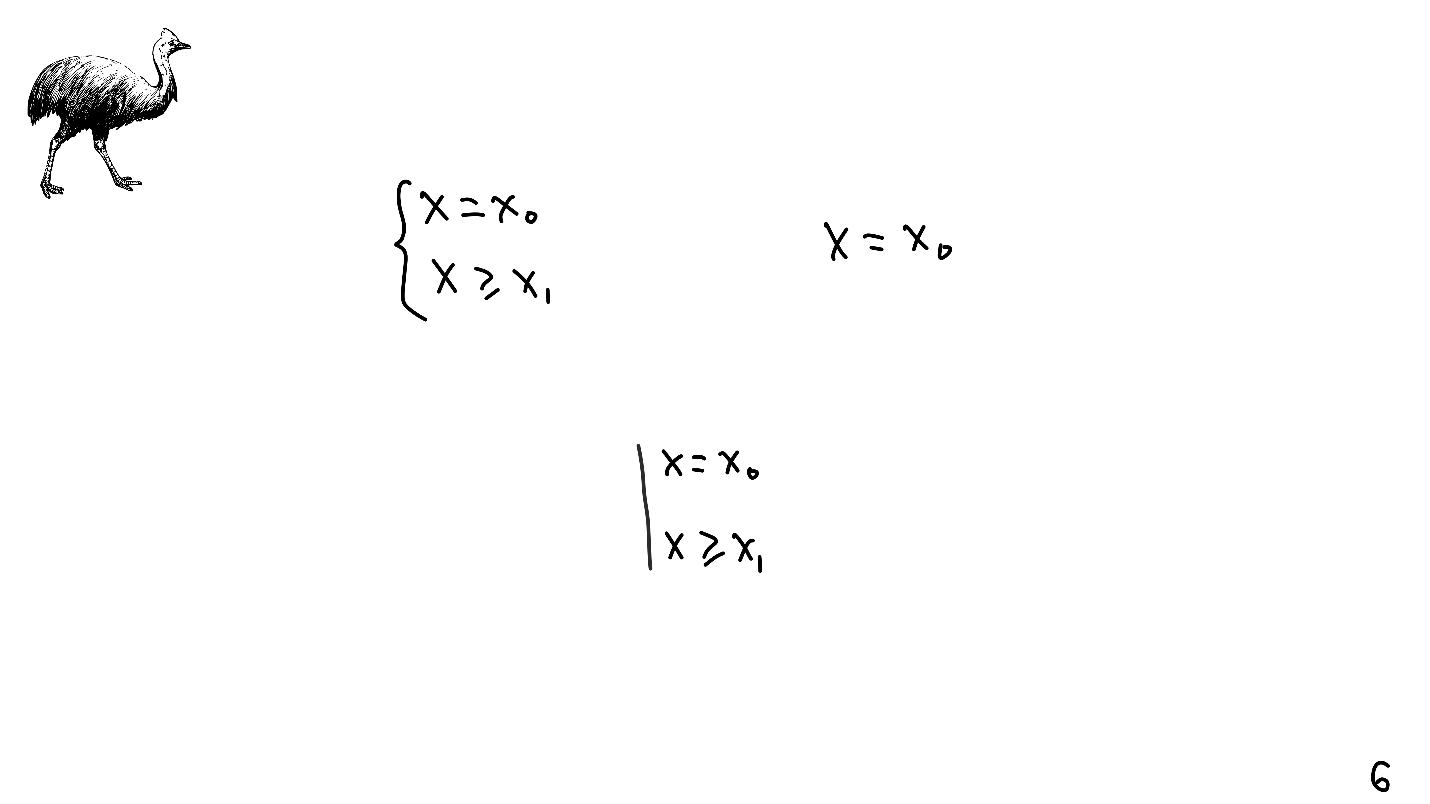
我们已经知道，奇怪的，危险的鸟没有意外地画在幻灯片的右上角。 为了纪念当然生活在澳大利亚的食火鸡（lat。Cassowary），在我们所有的iPhone中都采用了一种算法。

自动版式有其自身的局限性，我们将按优先级用颜色表示它们：红色-必填； 黄色-高； 蓝色-低。

布局图

制作演示文稿时，我在屏幕上放置了各种元素，例如食火鸡。 为此，我确定食火炉是一幅矩形图片。 您需要将其布置在具有轴和自己的坐标系的图纸上，为此，我确定了左上角，宽度和高度的坐标。



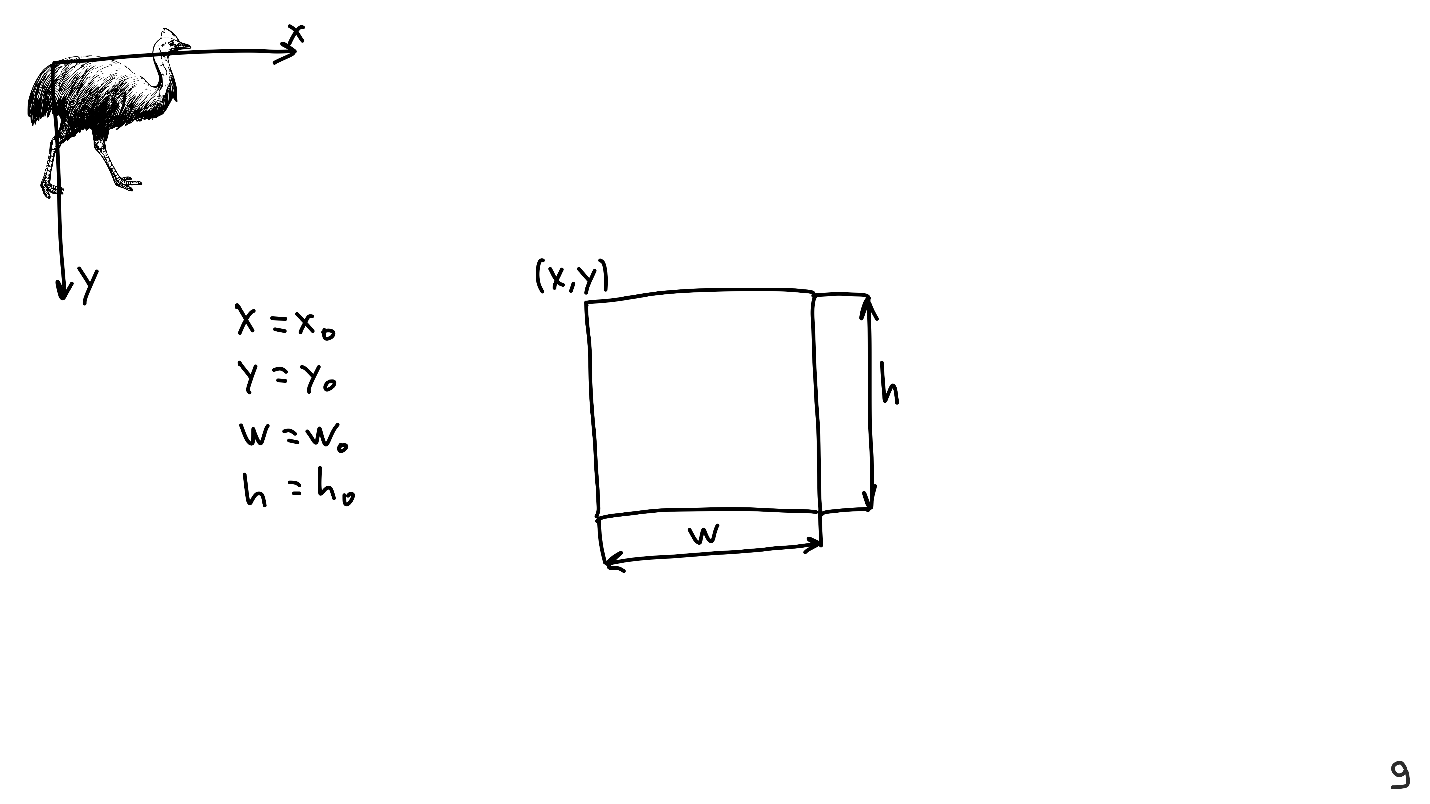
知道这四个值就足以表示任何视图。

算法1

在将食火鸡放在纸上的同时，我们毫不客气地描述了第一种布局算法：

• 确定坐标和大小；
• 将它们应用于UIView。

该算法有效，但是很难使用，因此我们将对其进行进一步简化。

假设下面是某些线性方程组的解决方案。



线性方程系统的特殊之处在于，在其上定义了许多运算：折叠线，将它们乘以常量等。 这些操作称为线性变换，在它们的帮助下，系统可以简化为任意形式。

线性变换的优点在于它们是可逆的。 这使我们想到了一个有趣且相当微妙的想法，由此开始了整个现代布局。

让一个视图-一个具有其坐标和大小的矩形。 我们要对其进行排列，以使中心与给定点重合。 我们使用线性变换对中心进行建模- 左上角的坐标+宽度的一半 。



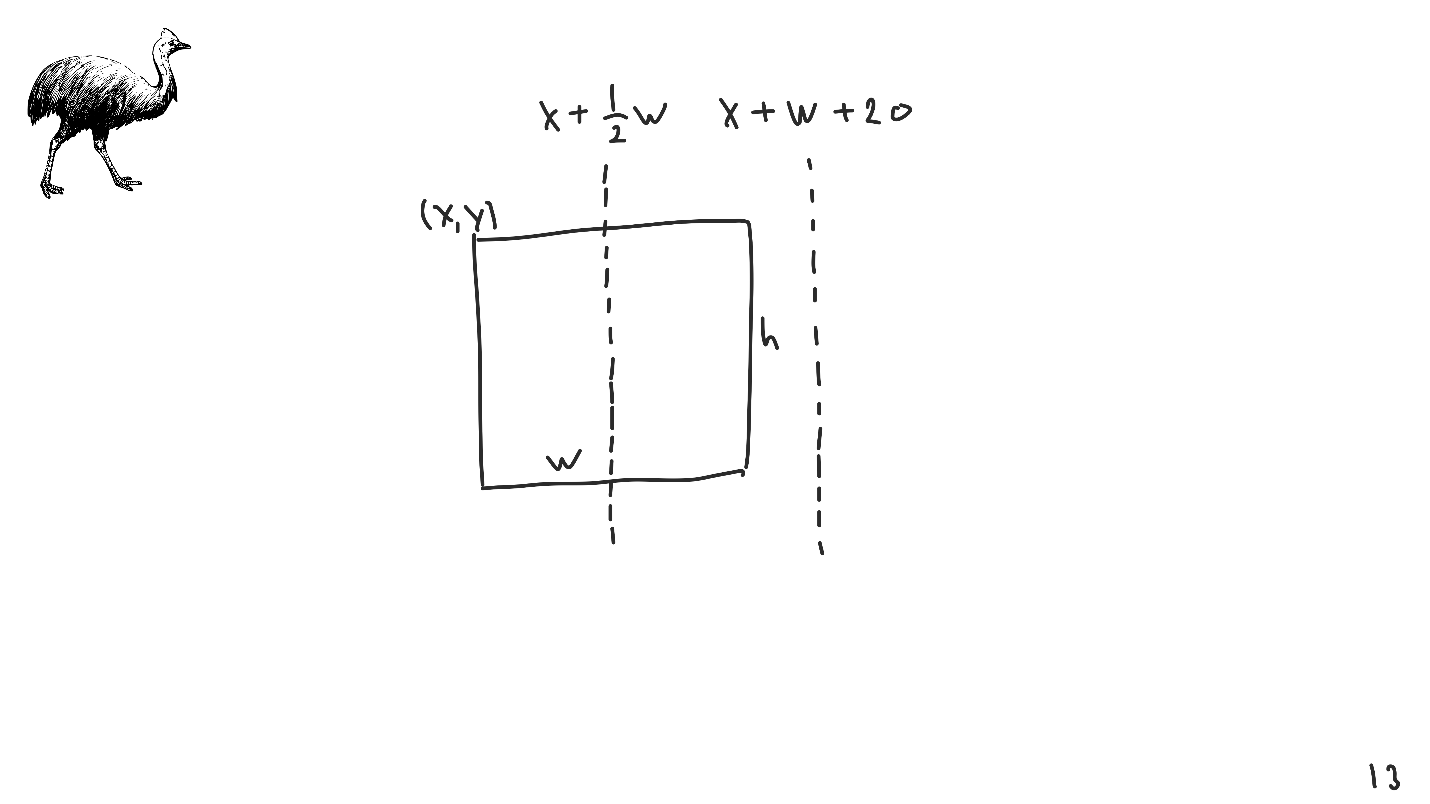
我们通过线性变换对中心建模，但不是：只有左上角点，宽度和高度的坐标。

同样，您可以模拟任何其他缩进，例如，从右上角起20个点。

线性变换的思想使我们能够创建各种排版系统。

考虑一个基本的例子。 我们写出一个系统，用来建立中间和右侧的坐标，宽度以及宽度和高度之间的关系。 我们解决了系统并得到了答案。



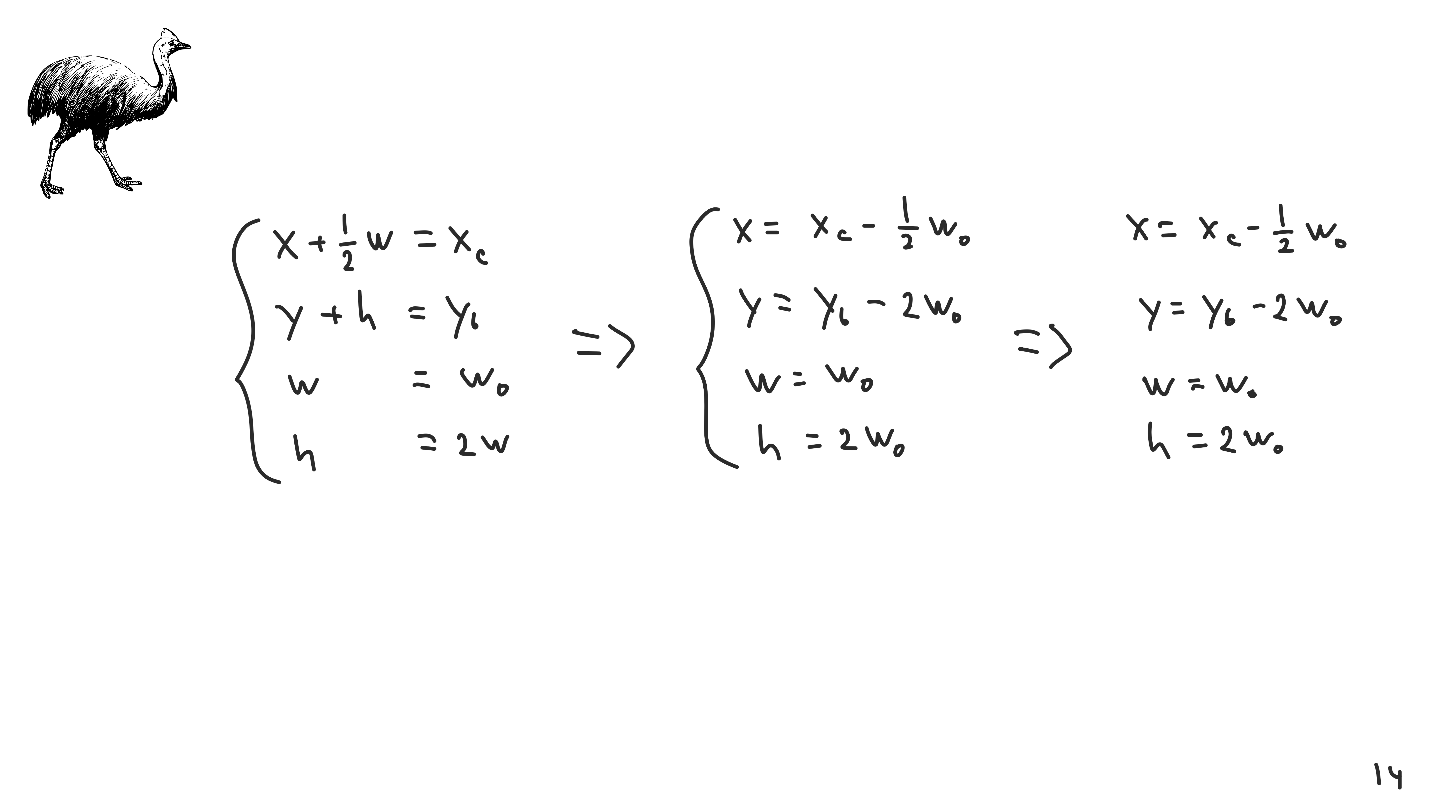
因此，我们来看第二种算法。

算法二

该算法的第二次迭代包含以下各项：

• 组成线性方程组；
• 我们解决了；
• 将解决方案应用于UIView。

想象一下，我们处于20世纪，当时计算机设备还处于起步阶段，而我们是第一个创建自己的布局系统的人。 发明，打包，提供给用户，然后他开始使用它-填写初始参数并将其传输到我们的系统。



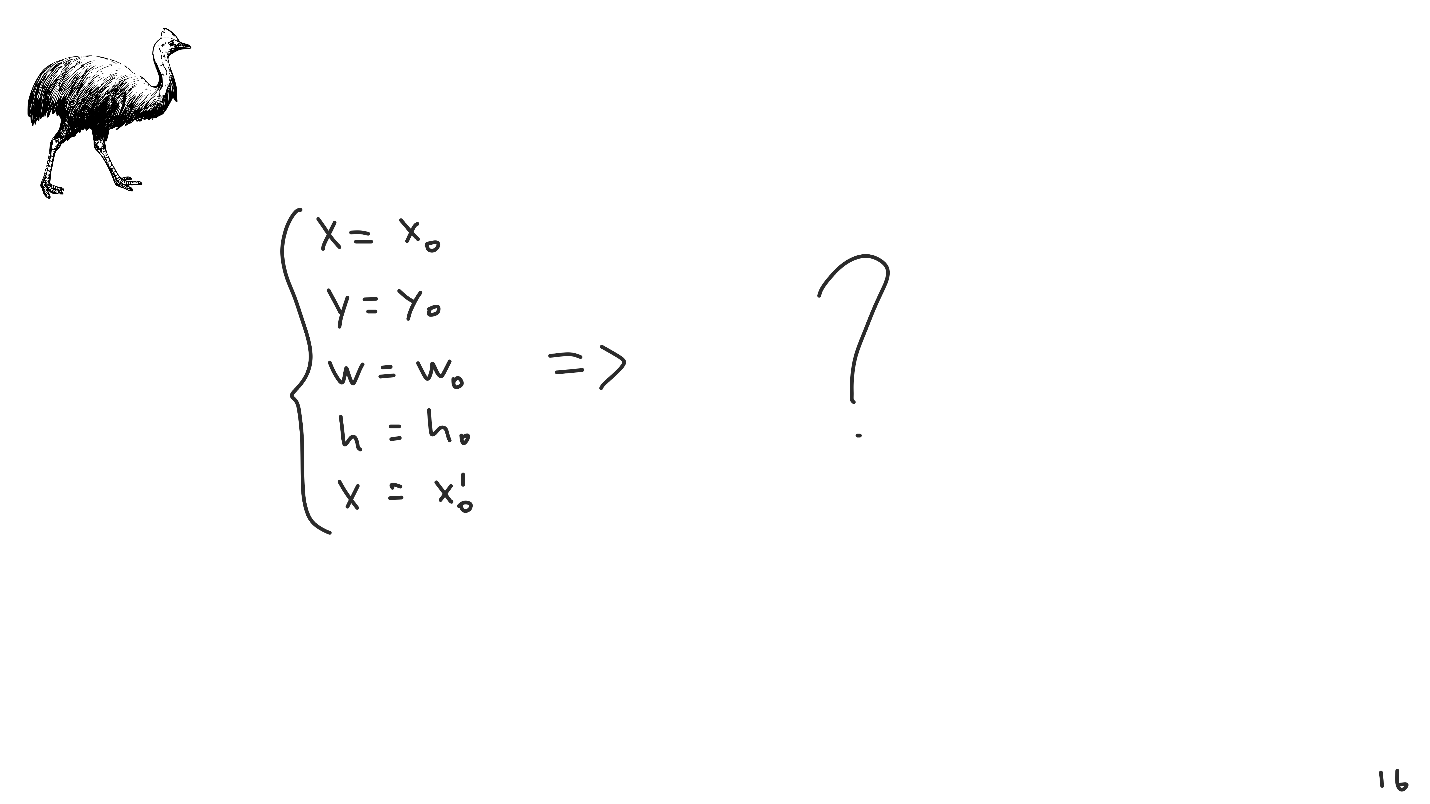
有一个问题-该系统没有单一解决方案。 这个问题并不罕见，绝对所有的布局系统都运行在其中，这被称为缺乏解决方案 。

解决这种情况的方法不多：

• 您可能会跌倒 -这是一种非常常见的方法。 那些使用MacOS的人都知道NSLayoutConstraintManager就是这样做的。
• 返回默认值 。 在布局的上下文中，我们总是可以返回全零。
• 一种更著名和精致的方法是防止错误输入 。 流行的布局系统（例如Yoga） （称为Flex布局 ）使用了这种方法。 此类系统尝试创建不允许错误输入的界面。
• 解决绝对所有问题的另一种方法是- 从一开始就重新考虑所有问题，并从一开始就预防该问题的发生 。 自动布局就是这样。

自动版面 问题陈述和解决方案

我们有一个矩形图片，并且要唯一标识它，我们需要4个参数：

• 左上角的坐标；
• 宽度和高度。

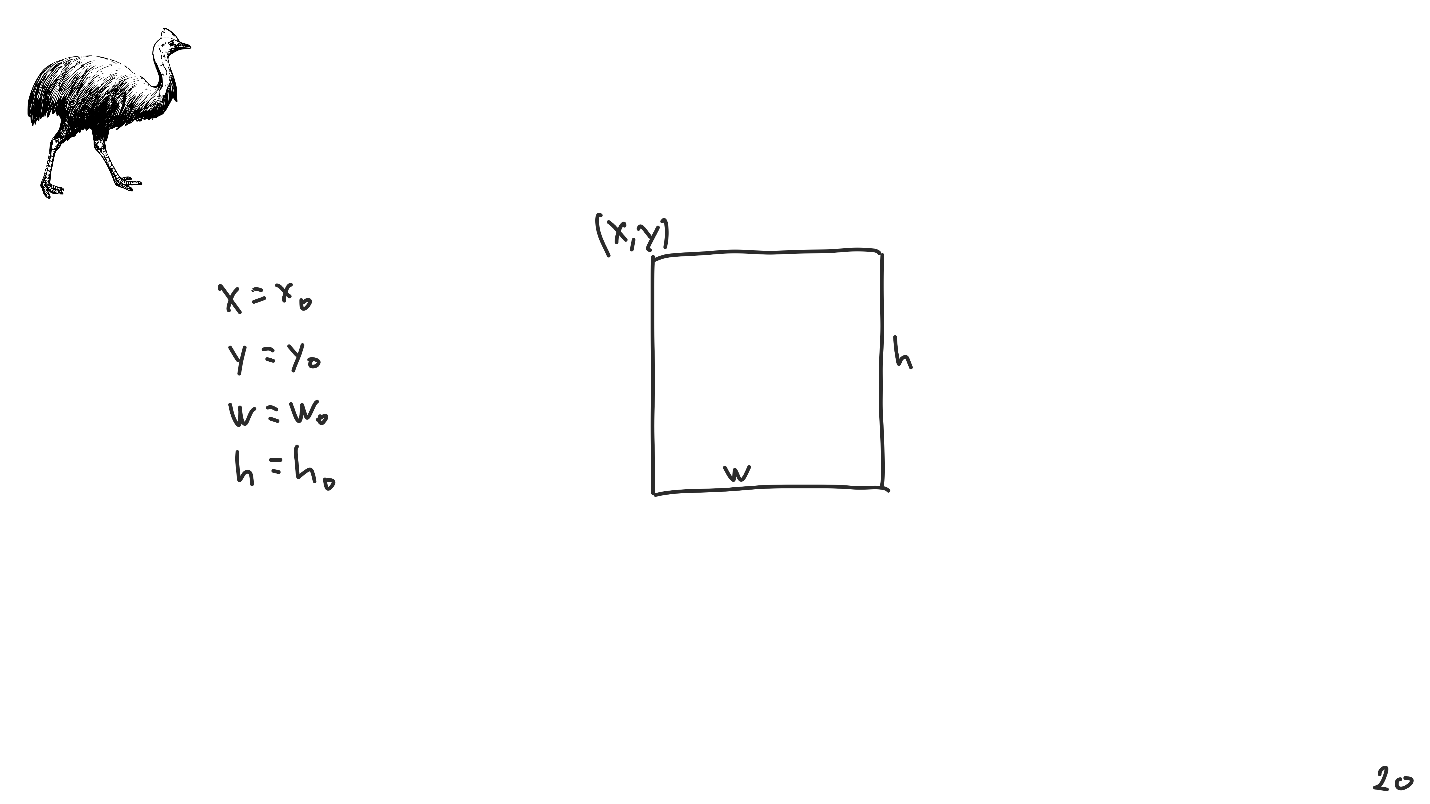
自动版式非常冗长。 与线性方程组相比，将所有内容放置在屏幕上要困难得多。 因此，我们将不失一般性地考虑一维情况。



一切都非常简单：空间是一条直线，可以放置在其中的所有对象都是一条直线上的点。 一个值： X = X _P足以确定点的位置。

考虑自动布局方法。 在其中设置了限制的空间。 我们想要得到的解决方案是X = X ₀ ，没有其他。

有一个问题-我们尚未定义具有限制的操作。 我们不能从记录中直接得出X = X _0的结论，我们不能将任何东西相乘或相加。 为此，我们需要将约束转换为可以使用的约束-方程和不等式系统。



自动版式可如下转换方程式和不等式的系统。

• 首先介绍2个非负且相互依赖的其他变量。 其中至少一个等于零。
• 约束本身被转换为符号X = X ₀ + a ^{+ -a-} 。

点X ₀   -系统解：如果⁺和^-等于零，则为true。 但是，这条线上的任何其他观点都是解决方案。

因此，有必要在整套解决方案中找到最佳方案。 为此，我们引入了一个功能-一个返回数字的普通函数，我们可以比较数字。 我们画一个图，请注意，我们最初想要获得的解决方案是最小的。

有一个线性规划问题 。 这正是“自动布局”对约束的作用，约束不仅表现为等式，而且表现为不等式。

不平等约束

在不平等约束的情况下，转换的发生方式与相等性相同：引入了两个附加变量，所有这些变量都收集在系统中。 只有功能是不同的，并且等于a-。



上图显示了这样做的原因-a = = 0 （从X ₀到+∞ ）的a ^+的任何值将是该问题的最佳解决方案。

让我们尝试将方程式和不等式的这两个限制合二为一-因为这些限制不是孤立存在的，它们会一起应用于整个系统。



对于每个约束，都会引入另外一对变量，并编译功能。 因为我们希望同时满足所有这些限制，所以功能将等于每个限制中所有功能的总和 。

我们收集了函数f，并看到解为X ₁ 。 如我们所料，做出了限制。 因此，我们来看第三种算法。

算法3

做某事，您需要：

• 建立一个线性约束系统；
• 将其转化为线性规划问题；
• 以任何已知方式解决问题，例如，自动版式中使用的单纯形方法 ；
• 将解决方案应用于UIView。

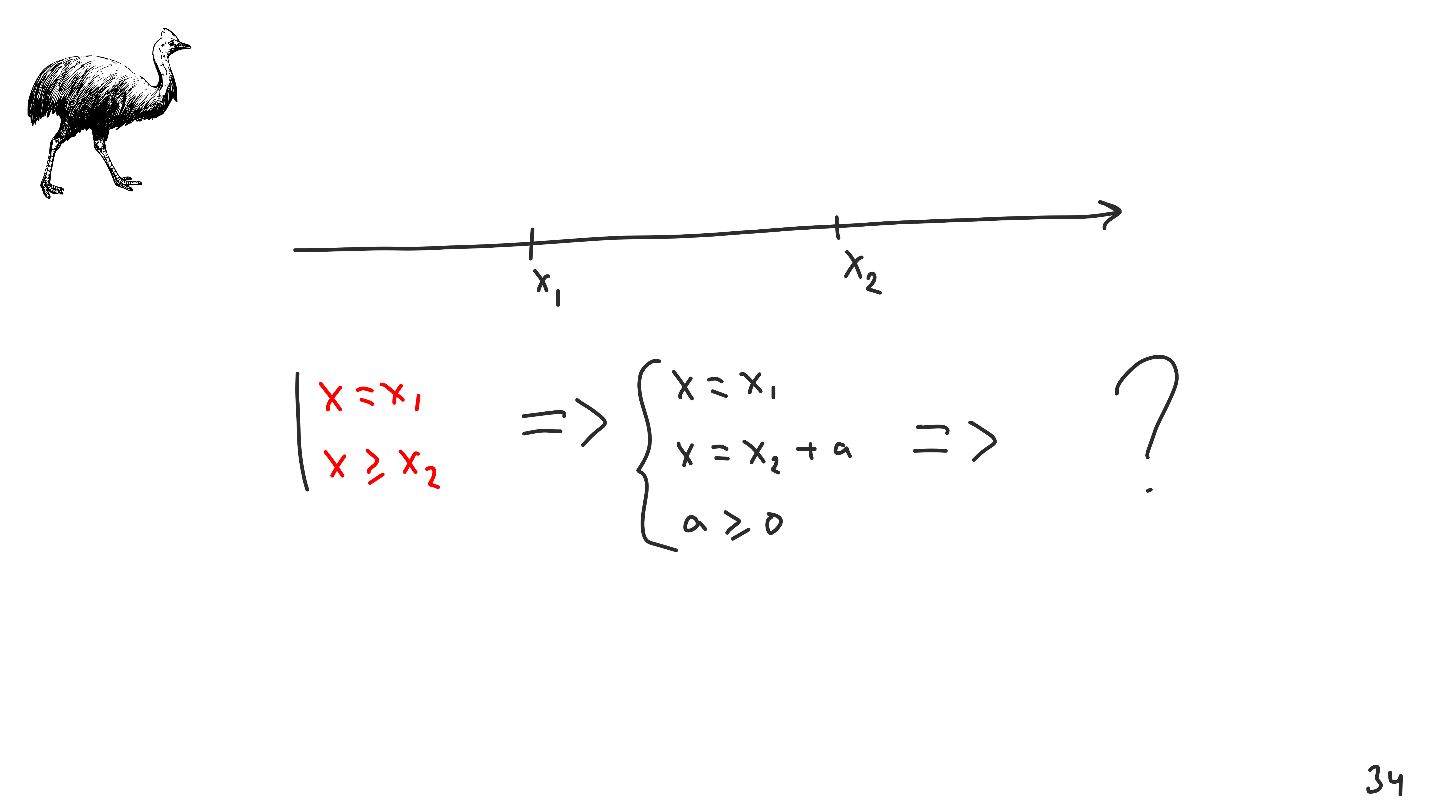
该算法似乎足够，但是考虑以下情况：我们更改约束的初始集合，以使第二个约束现在为X≥X ₂ 。



我们希望看到什么解决方案？

• X ₁ ？ 确实，在第一个限制中这样写： X = X ₁ ，并且该解决方案与第二个限制冲突。
• X ₂ ？ 第一个限制已经存在冲突。

为了摆脱这种情况，我们将执行我们已经知道该怎么做的转换。

新功能的图形看起来有所不同：从X ₁到X ₂的间隔中的任何点都是系统的正确有效解决方案。 这称为不确定性 。

不确定性

自动版式具有解决此类问题的机制- 优先级 。 我提醒您，黄色表示高优先级，蓝色表示低优先级。



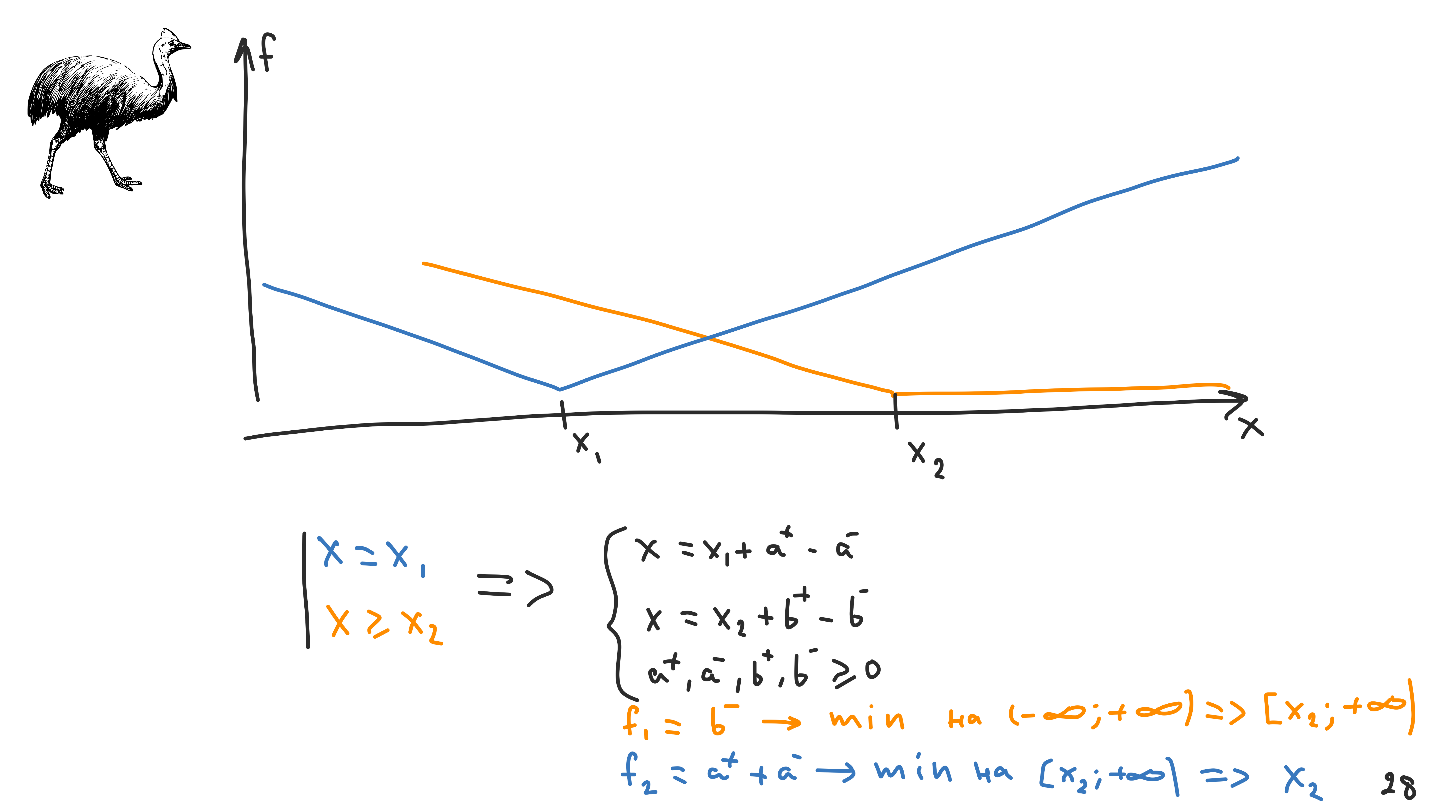
转换限制。 请注意，生成的系统仅为黑色。 我们知道如何使用它，并且其中没有有关限制的信息。 在功能方面，将有两个。 自动布局将首先最小化第一个，然后第二个。

在线性编程问题中，我们不是在寻找解决方案本身，而是在寻找可行的解决方案。 当然，我们希望该区域只有一点，并且“自动布局”的作用方式相同。 首先，它使（ -∞， +∞）上的最高优先级函数最小化，并在输出处接收可行解的域。 自动布局解决了已经在获得的允许值范围上的第二个线性编程问题。 这种机制称为约束层次结构 ，在此问题中给出点X ₂ 。

算法4

• 创建线性约束的层次结构；
• 将其转换为线性编程任务；
• 依次解决线性规划问题-从最高优先级到最低优先级。
• 将解决方案应用于UlView。

让我们再次看看上一个任务。 我们不是数学家，而是工程师，在这里应该混淆任何工程师。

这里存在一个严重的问题- 无穷大 ，我不知道它是什么。

“自动布局”模式下的Cassowary算法不是现有的机制，可以方便地落在“自动布局”任务上，但被认为是一种布局工具，它从一开始就提供了逃避无限性的特殊机制。 为此，发明了几种类型的限制：

• 参数是我们一直在使用的约束。 它们在原始文档（有时在Apple文档中）中称为首选项 （ 可选约束） 。
• 要求或要求-有优先权的限制。

让我们从数学的角度来看如何改变具有这些优先级的要求。



我们又有一条包含两个点的直线，第一个限制是X = X ₁ 。 在幻灯片上，它是红色的，也就是说，此限制具有所需的优先级-我们将其称为要求。

Auto Layout将其转换为包含一个方程X = X ₁的线性方程组。 仅此而已-没有线性编程任务，没有优化。

这种情况与不等式相似，但是稍微复杂一点-将会出现一个附加变量 ，该变量可以采用大于0的任何值。对于大于0的任何值，将满足此限制。 请注意，这里没有线性编程任务和优化。

让我们尝试将所有这些结合在一起，将两个需求放在一起，然后将它们转换为一个系统。 一位细心的读者指出，我们刚开始时遇到了同样的问题- 要求应该保持一致 。



需求类型的约束是一种非常强大的工具，但不是主要的，而是辅助的。 它是自动布局中专门引入的，用于解决无限间隔的问题，必须谨慎使用。

让我们尝试结合我们在一个系统中遇到的所有类型的限制。 假设我们想解决的问题不是在整条线上，而是在X ₀和X _3之间 。 将所有这些转换成线性方程和不等式的系统，我们得到以下结果。



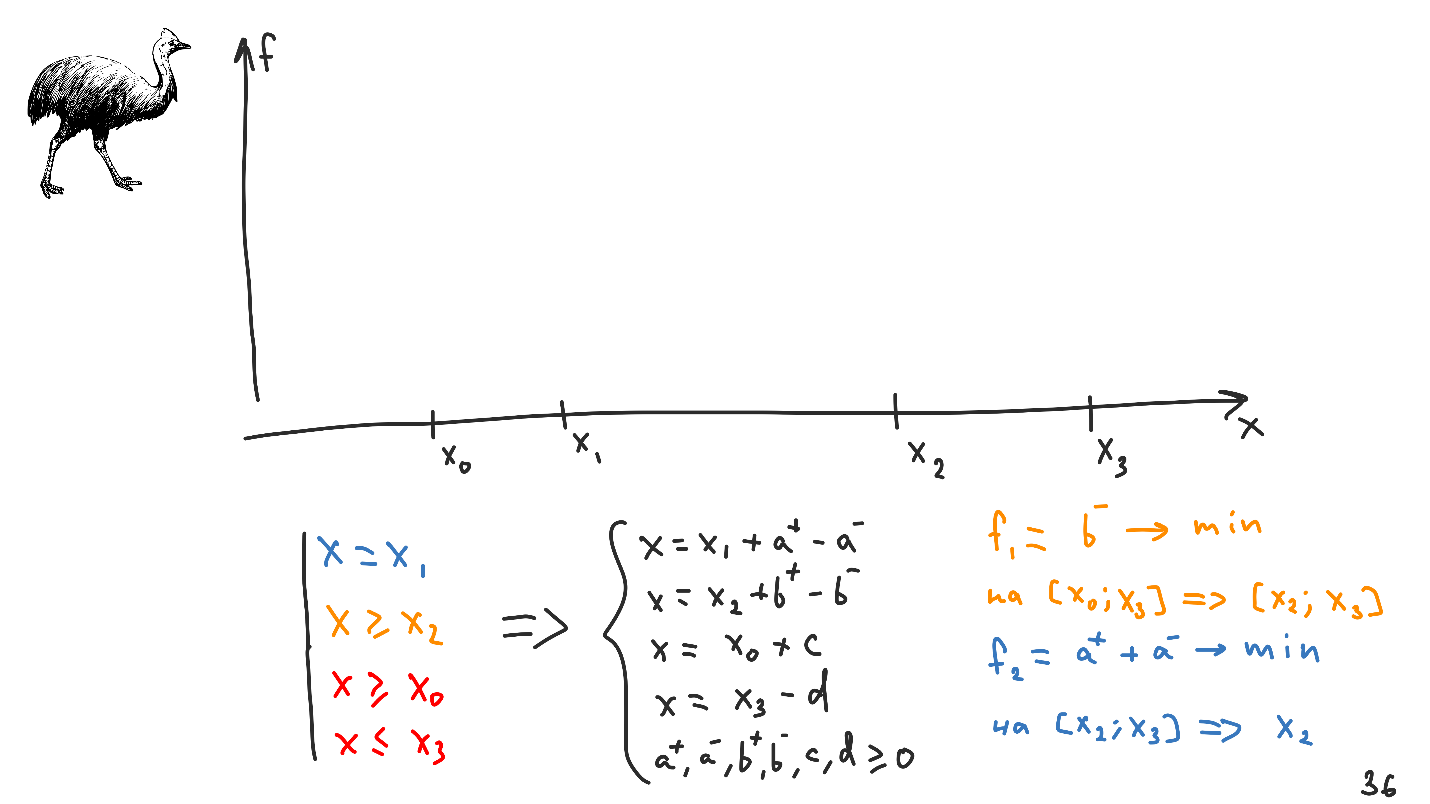
相对于先前的系统，添加了两个附加变量-c和d ，但它们不会进入功能，因为所需类型的限制不会以其原始形式影响功能。

任务似乎并没有太大变化-我们将与以前相同的值最小化，但是可接受值的初始范围正在变化，现在是X ₀到X ₃ 。

从数学的角度来看，需求（所需类型的限制）是在不修改系统功能的情况下将附加方程式引入系统的能力。

您需要对此非常小心，因为过多地滥用必需的约束将导致没有解决方案的问题 ，而自动版式将无法解决 。

我们到达最后第五个算法。

算法5

• 定义必要的限制-布局要求；
• 创建线性约束的层次结构；
• 将所有约束转化为线性规划问题；
• 解决线性规划问题；
• 将解决方案应用于UlView。

我们研究了Cassowary，这是Auto Layout中的一种算法，但是当实现时，会出现各种功能。

iOS功能

layoutSubviews（）中没有计算 。

它们何时生产？ 答：总是在任何时候计算自动版式。 当我们向视图添加约束或使用现代API方法来处理约束来激活约束时，就会进行计算。



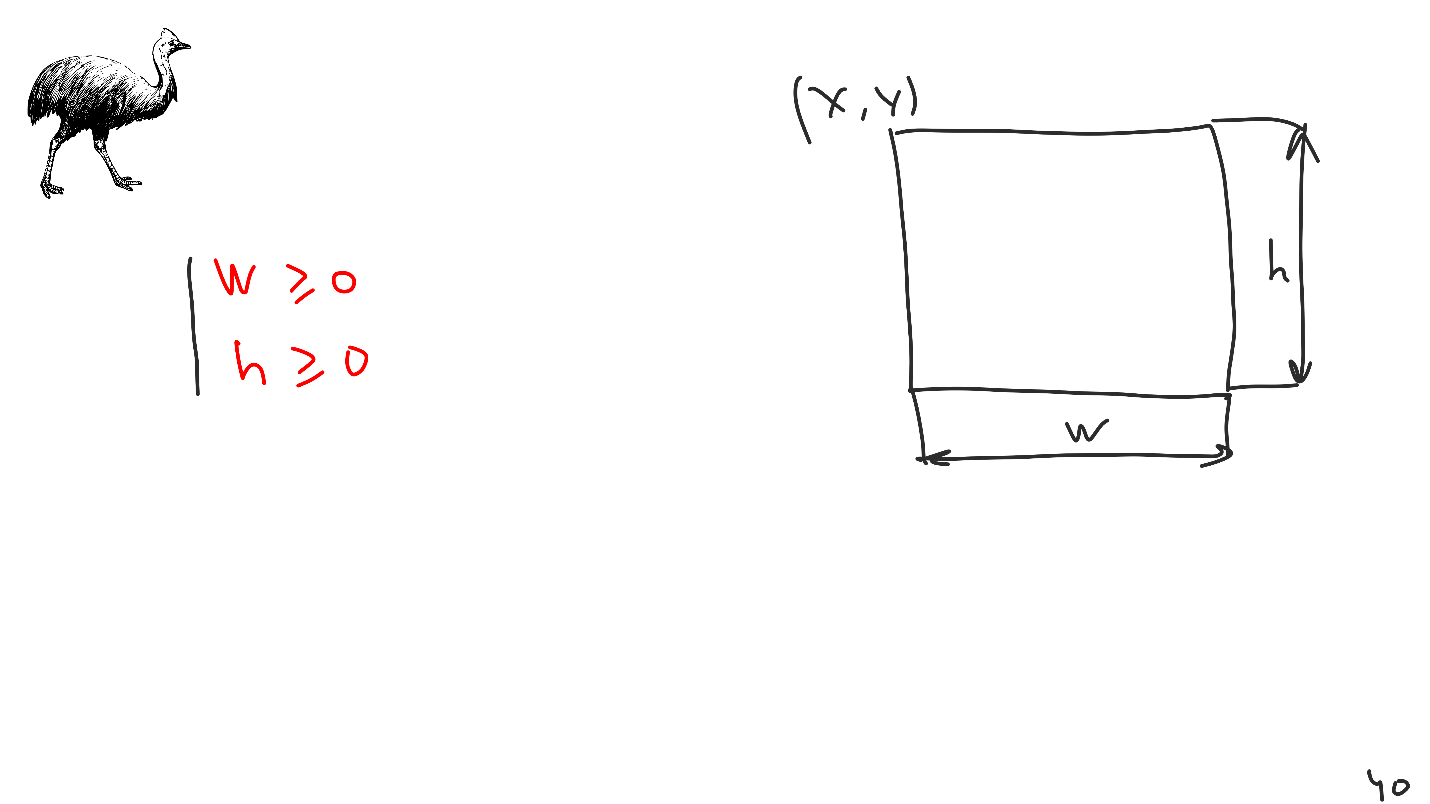
我们的视图是矩形，但是问题是该信息不包含在食火鸟内部，需要在其中附加嵌入。 我们具有引入其他限制的机制。 如果我们为每个视图引入一组宽度和高度为正的约束，那么我们将始终在输出处得到矩形。 这就是为什么我们不能用负尺寸的自动版式视图来弥补。

第二个功能是internalContentSize-可以为每个视图设置的固有大小。



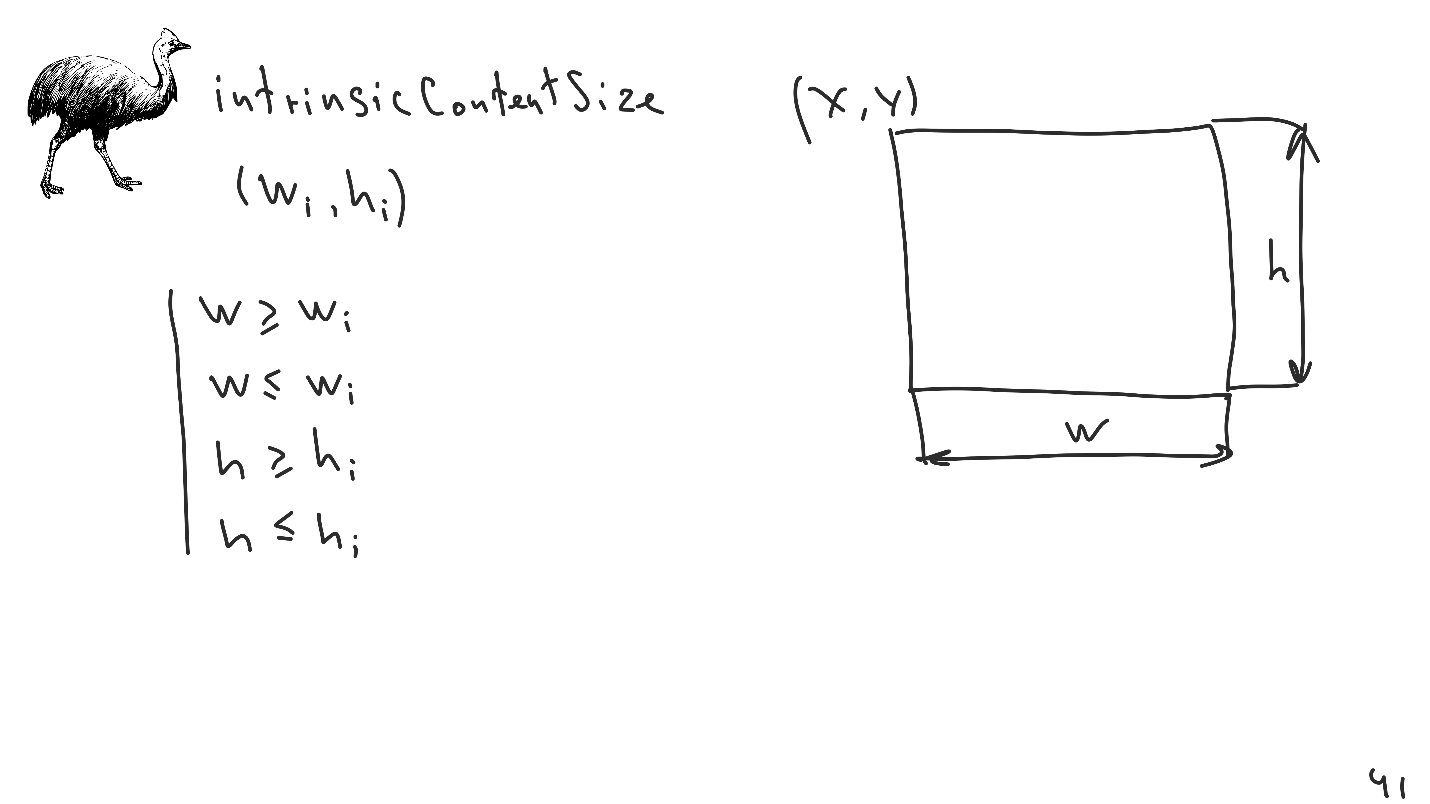
这是一个简单的界面，用于创建将放置在系统中的4个其他不平等约束。 此机制非常方便，它允许您减少显式限制的数量，从而简化了自动版式的使用。 通常被遗忘的最后一个最薄的点是TranslateAutoresizingMaskIntoConstraints。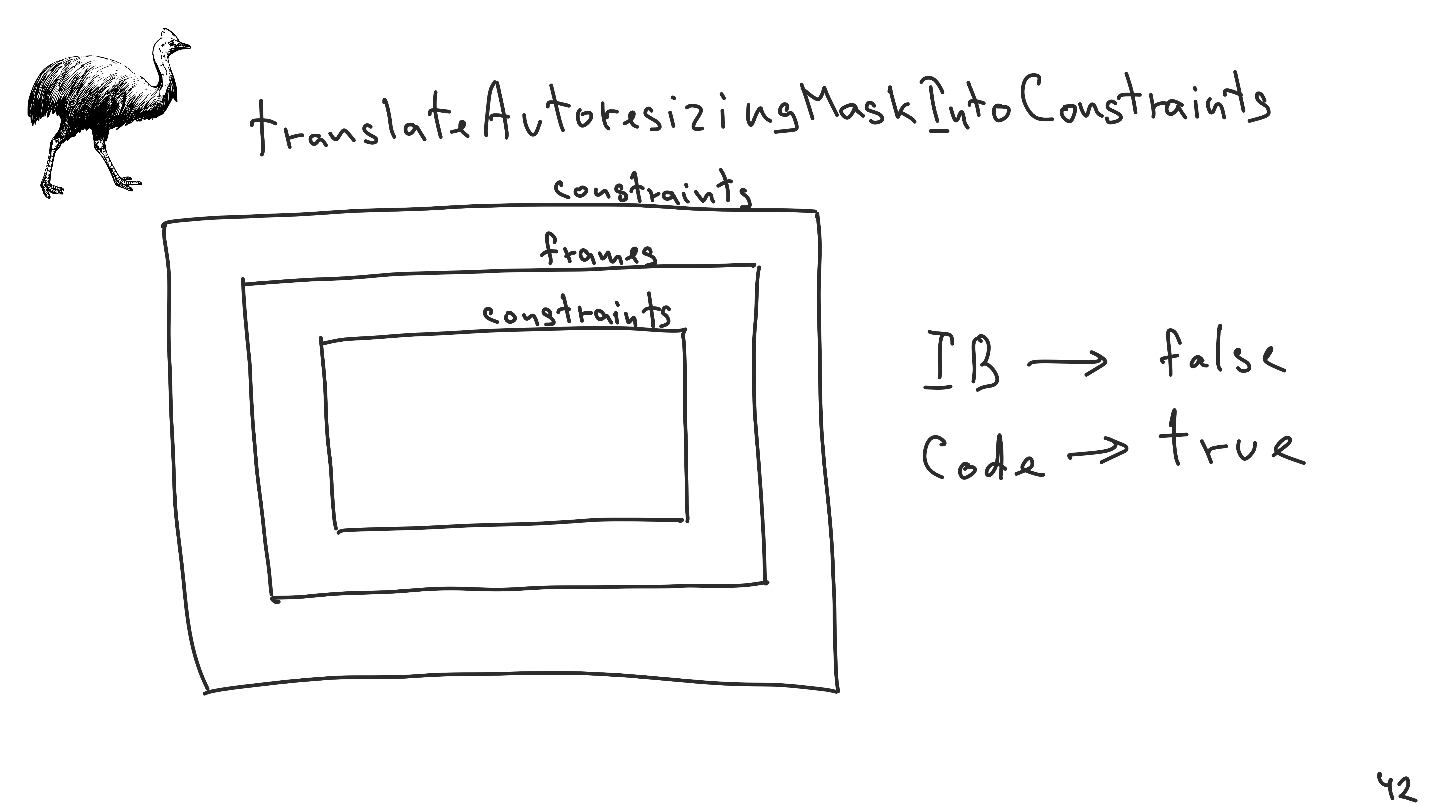



这是iOS 5时代引入的拐杖 ，因此旧代码在出现“自动布局”后不会中断。

想象一个情况：我们对约束施加了看法。 在视图内部，我们使用视图，该视图对约束一无所知，所有内容都在框架上排版，但是在视图内部键入视图，该视图早已被转换为约束。

我提醒您，Cassowary的“自动布局”任务没有框架，只有局限。

通过约束无法完全确定折叠在框架上的视图的大小和位置。 在计算所有其他视图的大小和位置时，将考虑不正确的大小，即使在“自动布局”之后我们将在此处应用正确的框架。

为了避免这种情况，如果TranslateAutoresizingMaskIntoConstraints变量的值为true，则会对框架上的每个视图施加附加限制。 这组限制可能因运行而异。 关于此集只有一件事是已知的-它的帧将是已发送的帧。

由于没有正确使用此属性，因此经常会出现不受约束的旧代码与具有约束的新代码之间的兼容性问题。 这些限制必定具有需求的优先级，因此，如果我们突然对这种具有很高优先级的视图（例如，需求）强加约束，那么我们可能会意外地创建一个没有解决方案的不一致的系统。

重要的是要知道：

• 如果我们从Interface Builder创建视图，则此属性的默认值为false 。
• 如果我们直接从代码创建视图，那么它将为true 。

这个想法很简单-创建视图的旧代码对“自动布局”一无所知，因此有必要进行修改，以便在新地方的某个地方使用视图时，它就会起作用。

实用技巧

总共有三个理事会，最重要的理事会开始。

最佳化

定位问题很重要。

您是否曾经遇到过优化屏幕的问题，该问题是在自动版式上进行的？ 很有可能不是，您经常会遇到优化表或Collection View内单元格布局的问题。

对自动版式进行了充分的优化，可以制作任何屏幕和任何界面，但是一次制作50个或100个是一个问题。 为了对其进行本地化和优化，让我们看一下实验。 这些数字取自最初描述食火鸡的文章 。


任务是这样的：我们一个接一个地创建视图链，然后将每个后续链与上一个链连接。 因此，构建了1000个元素的序列。 测量各种操作后，时间以毫秒为单位。 这些值非常大，因为自动布局是在80年代和90年代的交界处发明的。

通过收集这样的链，您可以执行以下操作：

• 一次添加一个约束，然后每次确定。 这将花费38秒。
• 您可以一次添加所有限制 ，然后才能解决系统问题。 此解决方案效率更高。 根据旧的数据，效率提高了70％，但在当前在现代设备上的实现中，只有20％。 但定性地一次性增加限制总是会更有效。
• 组装整个链条时，可以增加一个限制 。 从表中可以看出，此操作相当便宜。
• 最有趣的事情是： 如果我们不添加任何新限制，而是在现有限制之一中更改某些常量 ，则这比删除或创建新限制要有效一个数量级。

前两点可以描述为接口的主要计算，后两点则可以描述为下一个。

主界面计算

在这里，您可以使用批量添加约束的方法进行优化：

• NSLayoutConstraints.activate（_ :) -创建视图时，将所有约束顺序收集到一个数组中，进行缓存，然后一次添加一次。
• 或在Interface Builder中创建单元格。 他将为我们做所有事情，并进行附加的优化，这通常很方便。

后续接口计算

添加或修改约束是一项复杂的操作，因此最好不要更改约束集，而只需更改现有约束中的常数 。 :

• UIView — . view , Auto Layout. , , view, .
• — IntrinsicContentSize. , , .
• . , , .

, WWDC 2018S220 High Performance Auto Layout . — Apple , .

, constraints.

required , — , , . .

, .

:

• , . ( loader) — .
• , . , .

, , .

constraint required, . , , , . , .

— , . , — . - , , . Auto Layout , .

, . . , , , . layout, , , . .

— , Auto Layout, , .

, required, , . :

• , .
• , , .

, , , .

, . , , , . , — . .

— . , , , — , — required -.

:

Solving Linear Arithmetic Constraints for User Interface Applications
The Cassowary Linear Constraint Solving Algorithm
Constraints as s Design Pattern
Auto Layout Guide by Apple
WWDC 2018 Session 220 High Performance Auto Layout
UILabel API Auto Layout —
. Medium

顺便说一句，我们已经在AppsConf 2019计划中接受了安东的报告。让我提醒您，我们将AppsConf从秋季移到了春季，下一次对移动开发人员最有用的会议将在4月22日至23日举行。现在是时候考虑要演示的主题并提交报告，或者与主持人讨论参加会议和订票的重要性了。