Shipastik的历史

到处都有钉

我们称他为Spikey，在我今天的生活中，我不断遇到他：



它来自三维物体，即称为“菱形六十”的多面体。



但是它的历史是什么，为什么我们将其作为标志？

刺的起源

1987年，当我们开发Mathematica的第一个版本时，它的一项创新是可以基于符号描述生成与分辨率无关的三维图形。 在早期的演示中，这使我们能够生成令人惊讶的清晰的常规多面体图像。 但是，在接近Mathematica 1.0发行版时，我们想使用一些更令人印象深刻的示例。 因此，我们决定采用最后一个规则的多面体- 二十面体 -并通过赋予其星形或更正确的累积来使其更复杂。 是的，这就是30年前的第一个笔记本界面。



最初，这只是一个很好的演示，它当时在我们的计算机上运行很快。 但是不久之后，由它生成的三维对象就开始实际上被用作Mathematica的徽标。 1988年发布1.0版时，星状二十面体无处不在：



随着时间的流逝，对我们的恒星多面体的各种奉献开始出现-用不同的材料和尺寸制成：



但是，在发布Mathematica 1.0仅仅一年之后，我们就准备发布Mathematica 1.2，并且为了传达产品的复杂性，我们需要一个精致的徽标。 我们的开发人员之一Igor Rivin为双曲线空间中的多面体的博士论文辩护-由于他的努力，版本1.2的材料装饰有双曲线二十面体：



我的员工在1989年我30岁生日时给了我一件当时很现代的Shipastik T恤，并提供了我多年以来一直支持的报价：


“公司很有趣”

在发布Mathematica 1.2之后，我们可以在营销材料中找到一整套双曲正则多面体，但是随着1991年2.0版的问世，我们决定最喜欢双曲二十面体：



但是我们继续探索其他加标形式。 受达芬奇（Leonardo da Vinci）为卢克·帕乔利 （ Luke Pacioli ）的《论神的比例》一书中描绘的星状二十面体“木制模型”（以出乎意料的精确角度制作）的启发，我们订购了2.0版海报，其中布置了五个相交的四面体，以使它们的外顶点形成十二面体：



今天，通过查看我1991年的档案，我发现了“解释性”代码，很高兴看到它可以在我们的最新版Wolfram语言中轻松执行（尽管今天可​​以更优雅地编写）：



多年来，这已成为一种奇怪的习惯-为发布下一个主要版本的Mathematica做准备，我们将组织认真的会议，以进行“选择新的Shipastik”。 有时，您必须从使用完全不同的算法创建的数百个不同选项中进行选择：



但是，尽管调色板在变化，并且Shipastik经常反映系统中新功能的存在（尽管有些隐含），但我们拥有30年的传统，为双曲线十二面体选择选项：



最近，研究参数空间已成为惯例-尽管现在我们已经积累了数百个参数：



双曲十二面体有20个峰-非常适合在2008年庆祝Mathematica 20周年。 但是，当我们想在2013年25周年纪念日做类似的事情时，我们面临的问题是缺少具有25个顶点的规则多面体。 但是（实际上，使用SpherePoints函数[25]），我们能够创建一个近似的图形 ，并将其打印在公司所有员工的3D打印机上，其大小对应于员工的服务年限。

退出Wolfram | Alpha

在2009年，我们准备发布Wolfram | Alpha，并且系统需要徽标。 有很多概念：



我们想强调的是Wolfram | Alpha是通过计算而不是作为搜索引擎来工作的。 一段时间以来，我们想搭配齿轮一起使用。 但是我们也希望该徽标类似于长期使用的Mathematica徽标。 这引发了诸如“我们的将军发疯”之类的项目之一：从尖峰形式创建齿轮机构。

匈牙利的机械工程师Sandor Kabai长期使用Mathematica和Wolfram Language，他通过提出“尖齿齿轮”帮助我们：



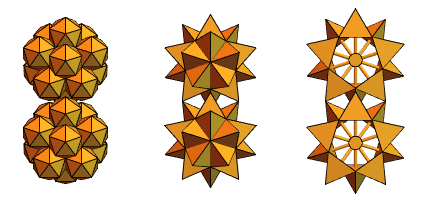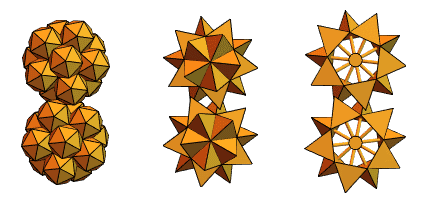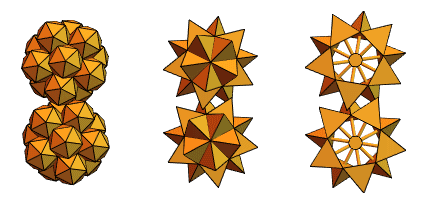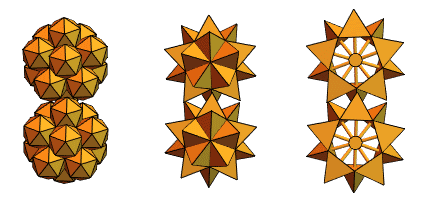
回到版本2的相交四面体，他创建了类似以下内容：



在2009年，3D打印机变得非常流行，我们认为最好为Wolfram | Alpha制作一个可以打印的徽标。 双曲多面体不适合-尖峰可能折断并构成威胁。 像第4版尖头这样的形状带有“安全尖头”，缺乏优雅感。

有一阵子，我们紧紧抓住齿轮的想法。 但是最后，他们认为值得再看一下普通的多面体。 但是我们可以选择哪种多面体呢？

当然，有无限多的可能的多面体。 但是对于我们的徽标，我们想选择一个对称的，并且在某种程度上是“正确的”多面体。 五个正面多面体（或“柏拉图实体”）-其面是相同的正面多边形-可以被认为是所有面中的“最规则”：



还有13个阿基米德几何体-它们具有相同的顶点，并且正则多边形（尽管类型不同）充当面：



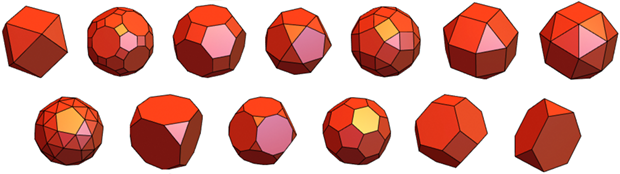
多面体的“正确性”有很多类型。 一个例子是“同质多面体”，1993年《数学杂志》的海报显示：



多年来，埃里克·温斯坦（Eric Weinstein）收集了该系列，并在1999年变成了MathWorld，他试图在尽可能多的多边形上添加文章。 在2006年，作为在Mathematica和Wolfram语言中包含各种系统化数据的一部分，我们开始在MathWorld中包含多边形数据。 结果，在2007年发布6.0版之后，其中出现了PolyhedronData函数，其中包含有关187个非凡多边形的综合数据：



在Mathematica和Wolfram语言中，您总是可以生成规则的多边形，但是现在它变得更容易了。 在6.0版中，我们还发布了Wolfram演示项目，该项目很快开始补充与多面体相关的各种演示。

其中之一是由我的女儿卡特琳娜（Katerina）十岁时制作的（今天她继续在几何学领域发展）：这些是“多面无尾熊”，被来自PolyhedronData []的所有多面体分解：



在这样的背景下，我们希望在2009年为Wolfram | Alpha“选择多面体”。 一切都是在2月6日星期五决定的，当时我开始独自工作。

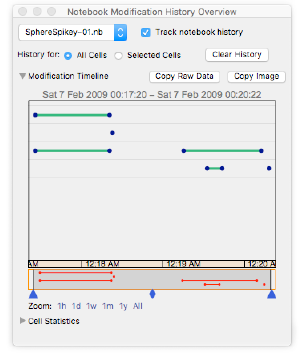
我保存了该笔记本，它表明我首先尝试实现将球体放置在多面体的顶点上的可疑想法：



但是，正如“ 笔记本历史记录”中记录的那样 ，仅两分钟后，我切换到纯多面体-它们都是橙色的，然后我们希望将其用于徽标：





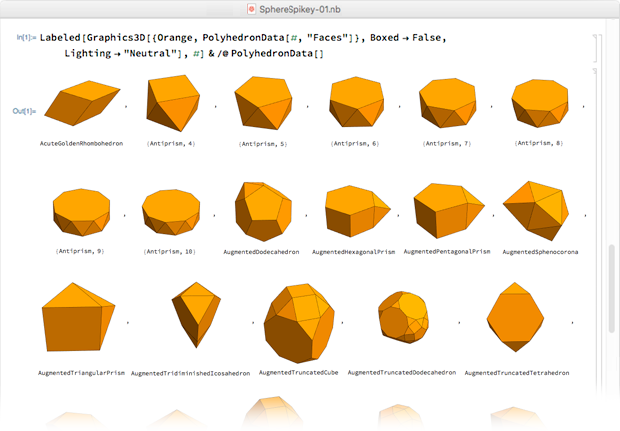
多面体按名称的字母顺序排列，在第28行出现-菱形​​六面体。



几分钟后，2009年2月7日，00：24：24，我发现了这个菱形六面体并将其变成对称位置，我们现在使用它：



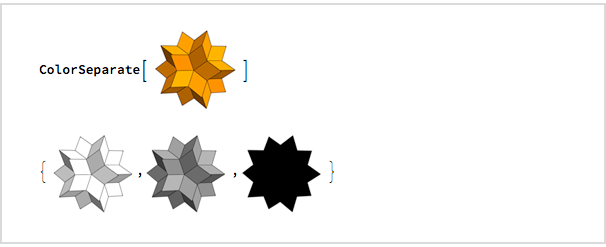
我想看看它在灰色和轮廓上的外观，四分钟后，我使用ColorSeparate找出了：



我立即开始写一封电子邮件，我在00:32发送：

我真的很喜欢RhombicHexecontahedron。 它具有有趣且非常对称的形状。 在我看来，它的精确度恰好适合我们，轮廓看起来非常合理。



显然，我只是从笔记本中复制了RhombicHexecontahedron（我怀疑我是否可以正确书写六边形[hexecontahedron]）。 从档案中，我知道这是我第一次写下多面体的名称，注定会成为我的最爱。

在Wolfram语言中，很容易获得菱形六面体的图像并进行处理：



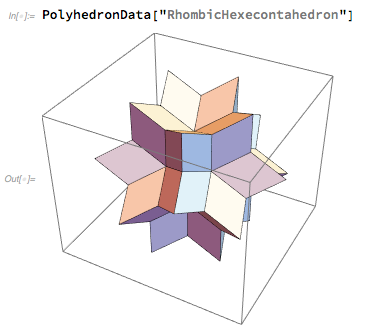
到周一，菱形六面体显然已经获胜-我们的视觉部门正忙于将其绘制为Wolfram | Alpha的徽标。 我们尝试了各种方向，但最终我们选择了“全视角”的对称位置。 （我们还需要选择最合适的角度的最佳“焦距”）。



像1.0版中的星状二十面体一样，菱形六面体也有60个面。 但是以某种方式，由于“五瓣”组合，它看起来更加优雅。 在选择这样的面部阴影上花费了很多精力，以便二维图形正确地反映了三维对象。 但是不久，我们推出了徽标的第一个正式版本：



她很快开始出现在各个地方，为了向我们的早期想法致敬，她经常以装饰有齿轮的背景为背景：



几年后，我们对边缘的阴影进行了轻微校正，从而创建了Wolfram | Alpha徽标，该徽标仍在使用：



菱形六边形

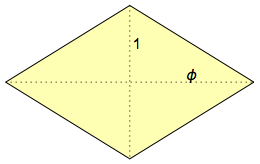
什么是菱形六面体？ 在英语中，它被称为hexecontahedron，因为它有60个面，andξηκοντα（hexekont）在希腊语中是“ 60”的意思。 它的面孔是金色菱形 ，之所以如此命名是因为它们的对角线根据黄金比例相互关联：φ=（1 +√5）/ 2＆sime; 1,618：



菱形六面体是二十面体和十二面体之间的有趣中间体（二十面体为十二面体）。 菱形六面体的12个内部顶点形成规则的二十面体，而20个外部顶点形成规则的十二面体。 二十面十二面体有32个面（由20个三角形和12个五边形的面组成），形成30个“中间峰”：



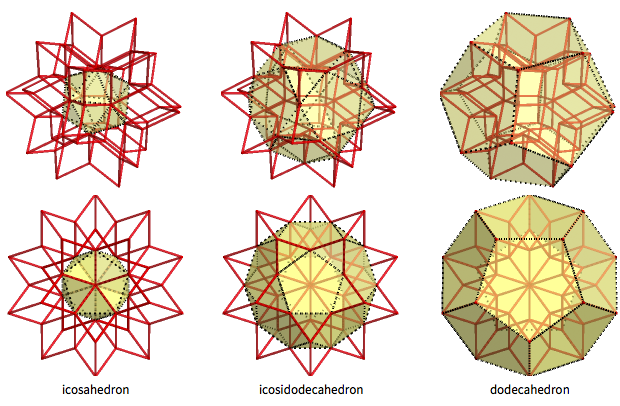
菱形六面体总共具有62个顶点和120个边（以及120-62 + 2 = 60个面）。 它具有三种类型的顶点（“内部”，“中间”和“外部”），分别对应于二十面体，二十面十二面体和十二面体的12 + 30 + 20个顶点。 在这些顶点处，3，4和5的边分别会聚在一起。 每个面都有一个“内部”顶点（在该顶点处有5个边线相交），一个外部顶点（其中在三个边相交处）和两个“中间”（4个边线相交处）。 外部和内部顶点是金色菱形的锐角顶点，中间顶点是钝角。

金色菱形的尖峰处的角度为2 tan ^-1 （φ ^-1 ）≈63.43°，钝角峰处的角度为2 tan ^-1 （φ）≈116.57°。 这样的角度允许您仅使用红色支撑（如十二面体的情况）从Zometool构造函数组装菱形六面体：



在60个“内部铰链”的菱形六面体的120个边缘中，二面角为4π/ 5 = 144°，而对于60个外部六面体，则为2π/ 5 = 72°。 外部和内部顶点收缩的角度分别为π/ 5和3π/ 5。

要绘制菱形六面体，您需要知道其顶点的三维坐标。 使用菱形六面体相对于二十面体组不变的事实可以方便地获得它们，因此您可以从一个金色菱形开始，简单地添加60个矩阵即可构成二十面体组的三维表示。 例如，这给出了{±φ，±1,0}，{±1，±φ，±（1 +φ）}，{±2φ，0,0}，{±φ，±（ 1 +2φ），0}，{±（1 +φ），±（1 +φ），±（1 +φ）}及其具有所有可能符号的循环置换。

除了菱形六面体的面孔是金色菱形之外，菱形六面体还可以由20个金色菱形六面体 （其中六个面都是金色菱形）构成：



还有其他方法可以从其他多面体创建菱形六面体。 可以从五个相交的立方体和与面接触的182个十二面体获得：



您无法布置菱形六十六面体的连续马赛克，但它们相互啮合良好（是的，我看到数十张纸质的Shipastik以此方式折叠）：



您还可以从中进行各种铃声和其他配置：



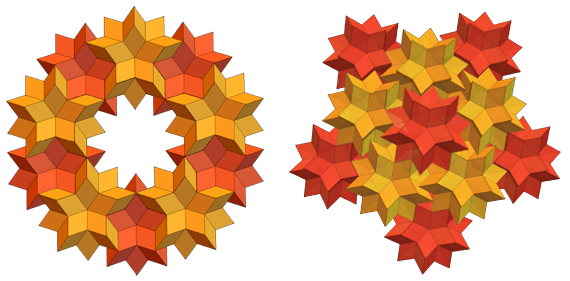
菱形六面体（RS）的近亲是菱形的三十四面体（RT）。 RS和RT的面孔是金色菱形。 但是RS有60个，RT有30个。这是一个单独的RT的样子：



几个RT可以完美地投资于RS的口袋中，结果类似：



前面提到的Sandor Kabay在2002年左右对RSh和RT产生了兴趣。 在Wolfram示范项目启动后，他与斯洛文尼亚数学家Isidor Hafner一起，在该项目中添加了100多个与RS，RT及其许多特性有关的演示：

尖纸模型

一旦确定Shipastik将成为RS，我们便开始制作他的3D模型。 现在，使用Printout3D [PolyhedronData []]函数执行此操作非常简单，并且可以在第三方资源上找到已经计算的模型 。

2009年5月，当Wolfram | Alpha发布时，我们已经手头上有很多3D Spikes：



但是，为这次活动后的第一个假期做准备，我们决定让每个人都有机会制作自己的三维Shipastik。 首先，我们考虑了20种带有塑料涂层的菱形体磁铁的选择。 但是它们的价格昂贵，而且结合得不好。

这使我们想到了用纸或薄纸板制成Shipastik的想法。 因此，起初我们想制定一个可以归入Shipastika的方案：



我的女儿卡特琳娜（Katerina）担任测试员（她仍然有一个测试样本），但很明显，折叠过程中出现了许多不舒服的情况，不清楚如何从一个位置移动到另一个位置。 您可以制作大量的布局（仅十二面体和二十面体就有43,380种布局）-我们认为也许可以从中选择更好的布局：



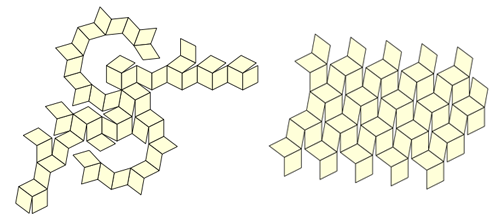
但是，当我们找不到这样的方案时，我们有了一个新的（虽然很明显）的想法：如果该模型可以吸引人，为什么不把它做成几块呢？ 我们很快意识到，为此，您只需要服用12种相同的此类物品：



在他们的帮助下，我们创建了“ 纸雕作品集 ”：



一项有趣的任务是编写易于理解的指令，但经过多次迭代，这些指令变得完善且简单：



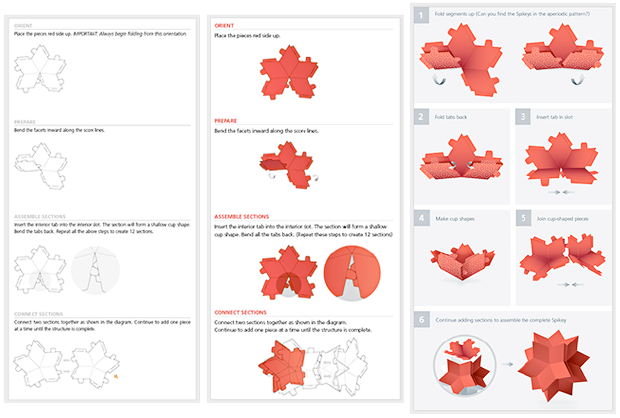
在将Shipastiks送给人们之后，我们的用户开始向我们发送“地面”上的所有Shipastik图像：

菱形六角形的路径

来自古埃及的多面立方体

不知道谁首先描述了柏拉图固体。 毕达哥拉斯人 （住在附近如此大型的多面黄铁矿晶体附近）也许是这样做的。 也许有人在他们之前做了这个。 也许这是雅典Teetet柏拉图的当代作品 。 但是，无论如何，到柏拉图时代（约公元前400年），已经知道了五种柏拉图固体。 当欧几里得写《元素》（约公元前300 g）时，这项工作的支柱之一就是没有其他常规多面体的证明。 该证明以从原始的欧几里得公理-32采取最多步数而闻名。

柏拉图式固体被用于骰子和装饰品。 但是他也被赋予了思考自然的中心角色-例如，柏拉图建议某种意义上，一切都可以由它们组成：来自立方体的地球，来自八面体的空气，来自二十面体的水，来自四面体的火以及天堂（“以太” ）来自十二面体。

那其他多面体呢？ 公元4世纪 亚历山大·帕普（Papp of Alexandria）写道，在阿基米德发现了另外13个“常规多面体”（显然现在称为阿基米德遗体）之前的几个世纪，尽管其细节丢失了。 一千年来，多面体几乎没有发生什么。 但是在15世纪，随着文艺复兴的开始，多面体突然又变得流行起来。 达·芬奇（Leonardo da Vinci）和杜勒（AlbrechtDürer）经常在艺术和设计中使用它们，重新发现了一些阿基米德人的遗体-并发现了新的多面体，例如二十碳十二面体。

但是，多面体的最大进步是约翰内斯·开普勒在十七世纪初的工作。 一切始于一个优雅的，尽管完全不正确的理论。 开普勒基于神学的假设，认为宇宙应该以数学精度创造，并建议当时已知的六颗行星沿着刻有并描述的五个柏拉图固体的嵌套球体运动：



开普勒在他1619年出版的《世界和谐》中指出，音乐，行星和灵魂的许多特征都是按照相似的几何关系和原理工作的。 为了证实这一论点，开普勒研究了多边形和多面体，特别是对构成完整集合的物体（如柏拉图固体）感兴趣。

他研究了用于铺装飞机的“接触式多面体”-例如发现了所谓的“ 巨大瓷砖 ”（由五边形，五角星形和十边形组成）。 他研究了“星状多面体”，并发现了各种星状版本的柏拉图固体（以及开普勒–庞索体 ）。 1611年，他出版了一本关于雪花的六角形结构的小书，作为他的一位顾客的新年礼物而写。 在这本书中，他讨论了球（和球形原子）的三维堆积，并提出了以下假设 ：三维空间中最密集的球堆积（我们经常观察到在商店的水果包装中的实施情况）是面心立方堆积（该假设仅在2000年后才得到正式证明）年-使用Mathematica）。

在各种开普勒软件包中，隐藏了不同的多面体。 让我们从任何领域开始，以其邻居为中心并连接其中心，以制成多面体的顶点。 在开普勒最紧密的包装中，有12个其他球体接触任何球体，并且从它们的中心获得了具有12个顶点和14个面的立方八面体。 但是开普勒还描述了另一种封装，密度降低了8％，其中每个球都被另外8个球覆盖，另外6个球非常接近。 如果将它们的中心连接起来，就会得到菱形的十二面体，它具有14个顶点和12个面：



发现这一点后，开普勒开始寻找其他“菱形多面体”。 在他发现的菱形十二面体中，菱形由成对的等边三角形组成。 但是到1619年，开普勒还研究了菱形的金色菱形，并发现了菱形的三十面，然后他在书中画出了菱形十二面体旁边的精美图像：



开普勒立即发现菱形多边形的应用：他想使用它们和一个立方体来构建嵌套球体的模型，该模型适用于伽利略在1610年发现的木星四颗卫星的轨道。

开普勒为什么不打开菱形六面体？ 我认为他离他很近。 他研究了非凸星状多面体。 他看着菱形的多面体。 但是，显然，对于他的天文学理论来说，菱形的三十面就足够了，之后他停止了搜索。

结果，当然，与多面体无关的开普勒定律成为了幸存下来的天文学的主要贡献。 但是开普勒关于多面体的工作（尽管是在错误的物理理论框架内进行的）仍然是对数学的永恒贡献。

在接下来的三个世纪中，发现了更多具有各种正确性的多面体-到XX年代初，数学家已经知道它们的许多类型：



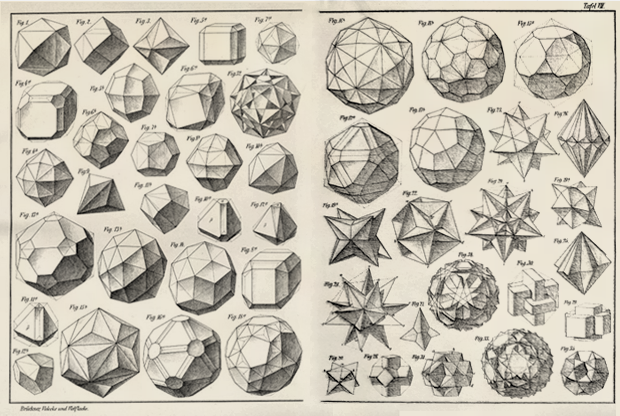
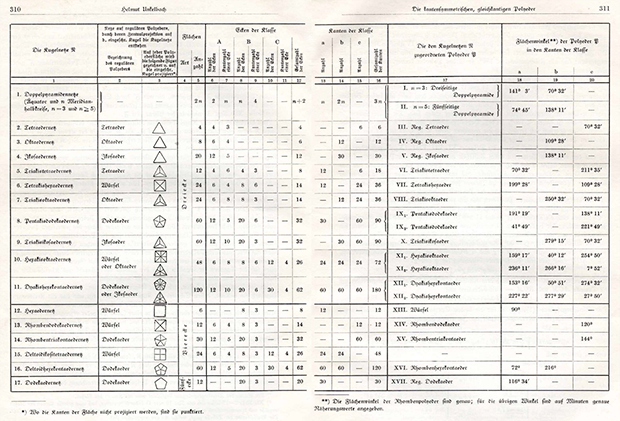
但是，据我所知，其中没有RS。 他的发现等待着Helmut Unkelbach的工作。 他生于1910年，1937年在慕尼黑大学为自己的数学博士学位辩护（尽管他首先学习物理学）。 他写了几篇关于共形映射的著作，并且-可能是由于对多面体的映射的研究-于1940年用德语出版了“边缘对称多面体”。

他解释说，他的目标是对满足正确性的特殊新定义的所有可能的多面体进行全面研究：所有边长均相同，并且位于多面体的对称平面内。 这项工作的主要结果是一张具有20种不同属性的多面体表格：


可点击

他们中的大多数人已经很有名。 但是Unkelbach挑出了其中的三个，他认为这是新的：两个六面体（十二面体），两个六面体（二十面体）和他称为菱形六面体或菱形六面体。 他清楚地将RSh视为他的主要成就，并附上他自己制作的模特照片：



他是如何带来RS的？ 他从十二面体开始，定义了十二个对称面：



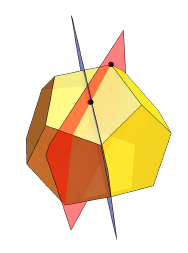
然后将其每个面分开：



然后，从本质上讲，他将每个脸部的中心挤出的距离等于到中心的通常距离乘以某个α：



对于α<1，所得面不相交。 但是对于大多数α值，它们的边并不相等。 仅在特定情况下会发生这种情况-当生成的多面体与RS完全重合时。

温克尔巴赫（Unkelbach）认为他的1940年研究工作是对“ k对称多面体”的更广泛研究的“热身”，其对对称性的要求不那么严格。 但是，当然已经有奇迹了， 第二次世界大战开始后 ，数学杂志在德国出版了-出版后不久，恩克尔巴赫被召到了最前沿，在那里他为德国舰队研制了声鱼雷长达数年之久。

他没有在多面体上发表更多作品，于1968年去世。多年后，他回到保形制图，并开始发表投票理论 ，认为这是建立运转良好的民主制度的关键，并认为数学家有义务使人成为现实。开始使用它。

但是，即使出现在1940年的著作中，如果1946年哈罗德·斯科特·麦克唐纳·科克塞特（Harold Scott MacDonald Coxeter）没有为相对较新的期刊《美国数学评论》（American Mathematical Reviews）撰写这篇作品的简短评论，RS也会永远留在那里。 他的评论列出了作品中提到的多面体，因为博物学家可以列出他在一次探险中发现的新物种。 最主要的是，他在那里描述了“杰出的菱形六面体”，并提到“其面的形状与三十面的面的形状相吻合，通过赋予其星形来获得它”。

在20世纪中叶，多面体并不是数学中的热门话题，但是Coxeter是它们的主要支持者-并且与研究它们的每个人都有某种联系。 1948年，他出版了《正确的政治科学家》一书。 它系统地描述了常规多面体的各个家族，尤其是星状的三十面多面体，实际上包含RS：



但是在他的书中，Coxeter没有明确提及RS，尽管他以一些多面体爱好者的引用而感到荣幸，但是RS仍然鲜为人知。

准晶体

晶体一直是自然界中多面体的重要例子。 但是到了19世纪，当原子理论获得越来越多的认可时，科学家们开始在晶体学和晶体中原子的排列领域进行越来越认真的研究。 多面体开始频繁出现，特别是在晶体中原子（“细胞”）的重复嵌段的几何形状的表示中。

到1850年，已知只有14种这样的几何形状-其中还存在一种基于菱形十二面体的几何形状。 它们因存在二阶，三阶，四阶或六阶对称而著称-本质上，这是由于空间只能填充某些多面体，就像只有规则多边形（例如正方形）可以填充二维平面一样，三角形和六边形。

那么其他非晶体材料（例如液体或玻璃）呢？ 自20世纪初以来，人们一直对那里至少存在近似五阶对称的可能性感兴趣。 不可能用正确的二十面体填充空间，但是有可能创建空间的二十个侧面的部分，它们之间的间隙很小。

这个问题一直没有解决，直到1980年代，当时使用快速冷却的铝和锰合金的电子衍射晶体学证明存在五重对称性。 已经存在实现这种对称性的理论，并且几年后，也出现了由电子显微镜拍摄的图像，在该图像上可以看到具有菱形三十面形状的颗粒：



而且，尽管人们想象着如何将这30个七面体相互结合，但出现了菱形六六面体-以“洞”的形式出现在12个菱形三面体簇中：



最初，它被称为20角星。 但随后它与多面体文献中的描述相关联，并被标识为RS。

同时，由菱形元素创建对象的想法越来越流行。 海洋学家，海洋波浪形成专家迈克尔·隆格·希金斯（Michael Longe Higgins）加入了大众业余爱好，并于1987年申请了一种基于菱形体元素的玩具的专利，可以从中组装出“开普勒星”（RS）或“开普勒球”（横摆三十）：



而且-尽管我现在才才知道，但我们在2009年就将菱形块体视为创建“ Shipastiks”的一种选择，它实际上是由Dextro Mathematical Toys（Rhombo.com）公司生产的，该公司在San Longge-Higgins的基地工作迭哥

用三维图形（甚至是带有二维图形的平面）成功填充空间的问题相当复杂。 从1960年代开始就已经知道，在一般情况下，某些形式的模板是否可以填充平面的问题是无法解决的。 （原则上，可以检查其中的1000个表格是否可以相互组合，但是我们考虑的表格越多，所需的计算资源就越多）。

像开普勒这样的人可能会认为，如果一组形状可以填充一个平面，那么这可以作为重复的图案来完成。 但是，在通常情况下无法解决此问题后， 罗杰·彭罗斯 （ Roger Penrose）于1974年提出了两种无需重复图案即可填充飞机的形式。 到1976年，Penrose（和Robert Ammann）提出了以下形式的简化版本：



而且，是的，这些形式看起来像菱形，尽管不是金色。 但是，当角度为36°，144°和72°，108°时，它们具有5倍和10倍的对称性。

这些菱形无法布置出重复的图案。 但是事实证明，他们可以布局以系统的嵌套方式构建的模式：



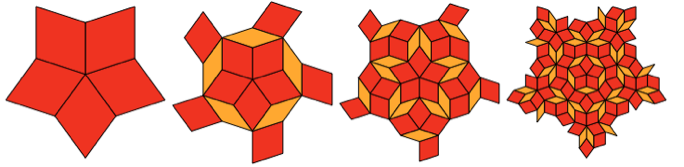
而且，是的，第三步的中间部分与扁平化的Shipastik非常相似。 但是它并不完全与之吻合，外部菱形的格式略有不同。

但是，它们之间仍然存在紧密的联系。 想象一下，我们不是从平面开始，而是从一个由金色菱形组成的三维菱形三十平方的一半开始：



从上方看，它看起来完全像嵌套Penrose马赛克设计的开始。 如果继续此过程，则会得到以下镶嵌图：



如果您从侧面看，它们仍然是相同的金色菱形：



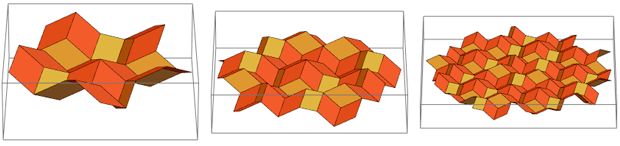
编译了这些“ Wieringa屋顶”中的四个之后，您可以得到RS：



这些嵌入结构与形成物理准晶体的真实方式之间有什么关系？ 目前尚不清楚。 但是，有趣的是，RS的提示在自然界中是如何出现的。

从历史上看，正是由于对准晶体的讨论，桑多·卡拜伊开始使用Mathematica研究RS，这导致Eric Weinstein发现了它们，并导致它们被包含在Mathematica和Wolfram语言中，这使我选择了其中之一作为徽标。 为了纪念这一点，我们在Paper Shipastik内部打印了Penrose马赛克：

扁平刺

随着Wolfram | Alpha的发布，我们的Wolfram | Alpha的Shipastik在2009年进入了世界。 但是，我们还有Mathematica的Shipastik，它已经发展了很长一段时间并不断发展。 因此，当我们在2011年建立新的欧洲总部时，有两个Shipastiks竞争其中的存在。

我们长期的艺术总监杰里米·戴维斯（Jeremy Davis）提出了以下建议：选择其中一个Shipastiks，仅使用其“骨骼”对其“理想化”。 从RS开始的决定很简单。 但是随后我们将其压平，因此出现了现在熟悉的徽标的第一个版本：

巴西的惊喜

当我开始这篇文章时，我以为整个故事将在这里结束。 毕竟，我已经描述了我们如何为自己选择RS，以及数学家如何提出RS。 但是在结束写作之前，我决定：“多年来，我将仔细阅读有关Shipastik的所有信函，以确保我没有错过任何事情。”

然后我注意到了2009年6月来自巴西艺术家Yolanda Kipriano的一封电子邮件。 她写道，她在一家巴西新闻杂志上看到了有关Wolfram | Alpha的文章，引起了Shipastika的注意，并提供了指向其网站的链接。 从那时起已经过去了9年多，但我仍然关注此链接，并为看到以下内容感到惊讶：



我继续读她的信：“在巴西，这个物体被称为Giramundos或“ Mandakaru花”，并且是由餐巾制成的，是一种艺术装饰品。”

什么 在巴西，有一个与Shipastik相关的传统，多年来我们都没有听说过它吗？ 很快我在网上发现了他的照片。 这些模型中的一小部分是用纸制成的，大部分是用织物制成的-但其中有很多：



我写信给我的巴西朋友，后者曾开发Wolfram | Alpha的第一个版本。 他很快回答：“这些物体看起来真的很熟悉。 令我感到羞耻的是，我没有足够的意愿比较两个和两个，”并向我发送了本地艺术品和手工艺品目录中的图片：



狩猎开始了：这些物体是什么，它们是从哪里来的？ 我们公司的某位人士说，他的祖母来自智利，他们钩针编织这种东西，总是使它们变成尾巴。 我们开始与在网上发布“民间造船者”图片的人取得联系。 经常发现他们是在商店购买副本的。 但是有时候人们说他们知道如何做。 每个人都有几乎相同的故事：他们从祖母那里学到了这一点。

至少在我们时代，收集民用尖峰的一种典型方法是从硬纸板上切割60颗钻石。 然后，每个人都需要用织物包裹，然后将它们缝在一起：



但是随后立即出现了数学问题。 这些人是否正确标记和雕刻了63°的金色菱形？ 通常不会。 它们由成对的等边三角形成60°的菱形-这是用于制造被子的标准菱形形状。 那么，荆棘谷是怎么来的呢？ 好吧，60°和63°之间的差异很小，如果将这些面缝在一起，则它们之间将有足够的空间来进行操纵，因此在不获得绝对精确角度的情况下制作多面体非常简单。 （也有准希帕斯蒂克，其中像在Unkelbach的建筑中一样，不是面孔，没有菱形，而是尖锐的“外部三角形”）。

互联网上的峰值被指定为不同的名称。 最常见的-Giramundos。 通常他们被称为Estrelas da Felicidade（“幸福之星”）。 它们有时被称为“摩拉维亚星”的事实令人困惑，但实际上， 摩拉维亚星是更锋利的多面体（最经常由菱形八面体制成），最近已成为照明设备而流行。

尽管进行了冗长的调查，但我仍然不了解民俗峰值的整个历史。 这是我发现的。首先，当今大多数流行的高峰都集中在巴西（尽管我们有关于它们在其他地方出现的故事）。其次，这个传统看起来很古老，它肯定早在20世纪就出现了，也许是在几个世纪之前。据我所知，它是像民间艺术通常那样从一个嘴传到另一个嘴，而且我还没有找到关于这个主题的任何真实历史文献。

某位宝拉·瓜拉（Paula Guerra）向我提供了最好的信息，她在一家旅游咖啡馆里卖了民间的穗状花序。十年前，她在历史名城圣路易斯帕拉伊亭（SãoLuis do Paraiting）经营的一家咖啡馆里。她说，来自巴西各地的人们来到她的咖啡馆，看到民间的尖峰，并说了类似的话“我已经有50年没有见过这种东西了。”

宝拉本人是从一个住在家庭农场的老妇那里学到的民间尖峰（她称之为“星星”），她从小就一直在做农户，并从母亲那里学到了这一点。她的过程-显然是一个典型的过程-包括将纸板收集在某个地方（最初就像帽子盒一样），用布覆盖这些碎片并将它们缝合在一起，以得到一个约15厘米大小的物体。

民间尖头有几岁？这只能通过口头传统来理解。我们发现有几个人看到了1900年出生的亲戚如何造出了astastik。宝拉（Paula）说，十年前，她遇到了一个80岁的女人，她告诉她200年前在咖啡农场长大的时候，整个架子上摆满了四代女性制作的民间穗状花序。

全国造船史的一部分似乎围绕着从母亲传给女儿的传统展开。据说母亲经常给孩子们做钉鞋作为结婚礼物。通常情况下，造船物是由小块的衣服和其他东西制成的，这些东西使女儿想起了自己的童年时代，就像今天的拼布被子对上大学的孩子一样。

但是，又发现了另一种带有民间尖峰的扭曲：母亲经常在缝制玩具之前就投入了钱，女儿可以在紧急情况下使用这些钱。女儿把她的石牌和缝纫用品放在一起，而丈夫几乎找不到他。一些尖刺被用作枕头别针-这可能是丈夫的另一个障碍。

哪些家庭支持制作民谣峰值的传统？自大约1750年以来，在远离城市的巴西农村地区，有许多咖啡和糖种植园。直到大约20世纪，农民们经常从偏远的城市带女孩到新娘那里来，通常很年轻，直到13岁。也许这些新娘（通常来自葡萄牙血统的好家庭，受过相对良好的教育）带有民间的烦恼。

显然，随着时间的流逝，这种传统传播到了较差的家庭，并基本上保留在那里。但是在20世纪中叶的某个地方-也许当该国开始出现公路，城市化开始，人们开始离开农场时-传统几乎消失了。然而，在1950年代巴西南部的乡村学校中，女孩在美术课中接受教育，制作带有特殊插槽的民间钉鞋，用作存钱罐。

在巴西的不同地区，民俗事件有着不同的历史。在南部边境地区（阿根廷和乌拉圭附近），有一种传统，即“圣星米格尔（她也是国家的船长）是由女性治疗者（即“巫婆”）在村庄制造的，她们在制造玩具时必须考虑患者的健康状况。

在巴西其他地区，玩具通常被称为花朵和水果的名称，与她的名字有些相似。在东北-FlorMandacarú（以仙人掌花的名字命名）。在热带湿地-杨桃（以杨桃果实为荣，有时也称为“热带星”）。在中部林区-Pindaíva（以红色刺状水果为荣）。



但是，流行的shipastika通常被称为Giramundo，这是一个相当古老的葡萄牙语单词，字面意思是“环游世界”。显然，这些玩具被用作护身符，在风中旋转时会带来好运。尾巴最近开始附着在它们上，但显然，习惯将它们挂在房屋中，可能是在假期。

通常不清楚导致造船术的哪些传统是原始的，哪些是最近出现的。在纪念圣路易斯帕拉伊汀顿悟节的节日游行中（当地名称为“三王之日”），民间的尖刺被用作伯利恒之星的象征-但这显然不是很古老的传统，显然也没有任何联系与宗教。

我们发现了一些在艺术展览中出现的民间尖峰的例子。其中之一是由建筑师Liina bo Bardi组织的，于1963年举行，致力于巴西东北部的民间艺术。另一个是我所见过的最大的三维峰值，它是由建筑师兼设计师Vladavio Imperio于1997年组织的：



那民间的尖峰是从哪里来的呢？我还是不知道它们可能出现在巴西，它们可能来自葡萄牙或欧洲其他地区。他们使用织物和缝制件进行制造的事实可能是支持其非洲人或美国原住民血统的论点。

一位制作手工艺品的现代手工艺人说，她的曾祖母-曾制造此类玩具，出生于19世纪末-来自意大利的一个地区，名为罗马涅（Romagna）（还有人说她从祖母那里学到制作手工艺品，祖母来自法裔加拿大人）。我认为，民间尖峰在欧洲曾经很普遍，但在许多世代之前就已经消失了，这种传统并没有在那里延续下来。尽管在上个世纪的欧洲绘画中出现了大量不同的多面体，但我不知道其中有任何希斯塔斯蒂克的图像（在伊斯兰艺术中我也没有见过希斯塔斯蒂克）。

但是我很确定民间尖峰有一个起源点。这样的事情几乎不会被发明两次。

我必须说，这不是我在艺术领域的第一次尝试。对第一个嵌入式图案（Sierpinski）的搜索最终取得了成功-最终使我进入了意大利教堂的地下室，在这里，我观察了如何使用可追溯到13世纪的石材马赛克实例逐渐发现这种图案。

到目前为止，Shipastik并没有那么轻松地放弃-并使情况复杂化的事实是，它基本上是由织物制成的，不如石材好。

尖刺栩栩如生

无论其起源如何，Shipastik都扮演着强大而有价值的徽标的角色。但是有时候重振Shipastik很有趣-多年来，由于各种原因，我们制作了各种个性化的Shipastik：



在使用Wolfram | Alpha时，系统通常会显示几何的Shipastik。但有时您的请求会对其进行动画处理-例如，在pi日请求π：

blog.stephenwolfram.com/data/uploads/2018/12/spikey-lives-happy-pi-day-video.mp4

永远钉

多面体是永恒的。可以从500年前的图像中看到它们，它看起来像我计算机上的多面体一样清晰现代。

我花了很多时间搜索抽象计算事物（例如，蜂窝自动机）。他们也有一些永恒。但是对于他们，我没有发现任何历史证据。像抽象对象一样，它们可以随时创建。但是，由于我们的概念平台和工具，它们今天才出现-从来没有人看到过它们。

多面体的悠久历史和恒定性已有数千年的历史。在外观上，它们类似于宝石。找到某种正确的多面体就像在所有可能形状的几何宇宙中找到宝石一样。



RS就是这样令人惊奇的宝石之一，通过研究其性能，我开始更加欣赏它。但这同时也是具有人类历史的瑰宝-看到这样的抽象（如多面体）如何使世界各地的人们具有如此不同的历史和目标，这是一件非常有趣的事情。

谁是第一个发明菱形六面体的人？我们不知道，也许永远都不知道。但是现在我们有了它，他将永远和我们在一起。我最喜欢的多面体。