春季文明，1/5

###第1部分。金色的“ Ku”

大约六岁的时候，我掉进了20世纪中期卡车上的一位祖父指南^[50] 。 牢固，印在光滑厚纸上的稀有书籍。 国家崩溃，战争和旅行之后，我祖父唯一留下的记忆。



该参考书包含许多有趣的性能特征，因此我从很小的时候就开始熟悉“负载能力”这个词。 当我父亲散步时提到，任何一辆卡车的重量都与其自身重量一样大，我记得这一点。 他想起了，后来很感兴趣。

父亲说的没错。 对于60年代的卡车，此规则的实现具有令人惊讶的准确性：



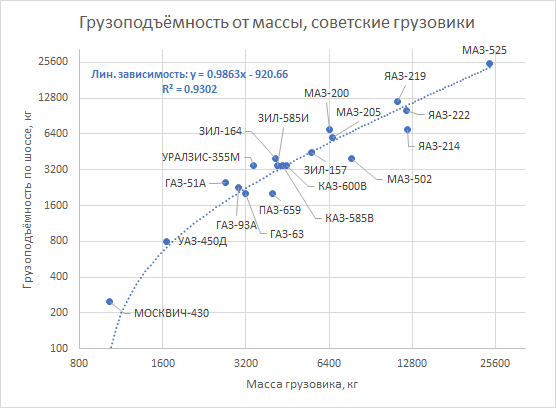
更奇怪的是，对于完全不同于卡车的车辆也观察到了这种模式。

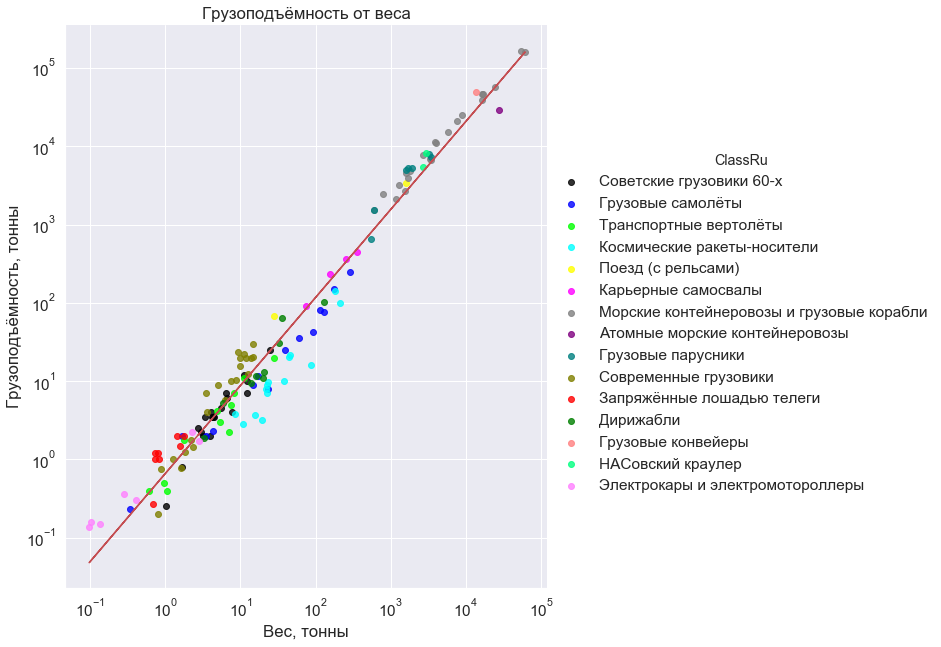
起初，为了好玩，我把货运飞机放在了时间表上。 并感到惊讶。 我开始添加其他车辆。 骑马，漂浮和飞行，建于19、20和21世纪，致力于利用热能，原子能，风能甚至马匹的能量。 结果呢 弱功率（指标1.125），如果不只是线性的，则依赖。 重量从数百公斤到六万吨。 当然，如果存在偏差，哪里可能没有偏差，有时可达10倍，但是按六个数量级，这显然是一件小事。

这就是这种依赖性，它挤压到一个巨大的空白区域的对角线：


在图表上注明：货机； 运输直升机； 现代和世纪初的飞艇； 太空运载工具（低轨道）； 60年代的苏联卡车； 现代矿用卡车； 俄罗斯，美国，中国和印度的现代卡车； 电动汽车和踏板车； 火车（带铁轨）； 核集装箱船； 集装箱船和货船（不是油轮）； 航行17至20世纪的货船; 矿石转移输送带； 纳索夫斯基拖拉机开始用于导弹出口； 最后是手拉车。

如果输入Q的值（定义为相对于车辆干重的已运输货物的质量），则每个组的外观如下：



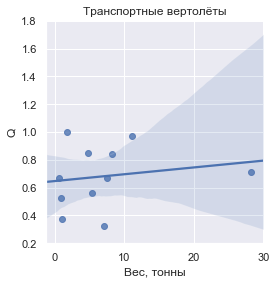
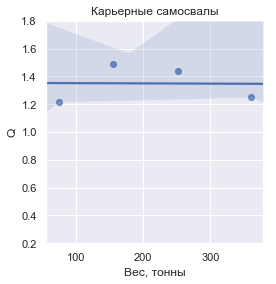
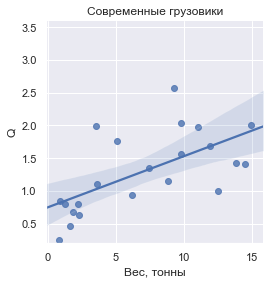
Q值以数字表示：

资产类别	平均Q	标准偏差Q
货运飞机	0.667091	±0.206162
运输直升机	0.681605	±0.225062
现代和世纪初的飞艇	0.842673	±0.374622
太空运载火箭（低轨道）	0.372446	±0.155810
60年代的苏联卡车	0.777435	±0.232425
现代矿用卡车	1.349610	±0.136840
俄罗斯，美国，印度，中国的现代卡车	1.293679	±0.604313
电动卡和踏板车	1.098433	±0.343791
火车（带导轨）	2.275989	±0.205999
核集装箱船	1.035233	±不适用
海运集装箱船和货船（不是油轮）	2.556004	±0.378040
航行17-20世纪的货船	2.488461	±0.671785
货运传送带	3.703704	±不适用
纳索夫斯基拖拉机发射导弹	2.355919	±0.525174
马车	1.203061	±0.389183

可以看出， Q虽然不是到处都严格地是单数，但在每个组中都趋于接近于统一的共同值。


在我看来……很神秘。 为什么木制帆船，铝制电动汽车和容纳十万辆电动汽车的原子集装箱船会全部或多或少地增加其重量？ 是什么使我们制造出质量Q≈1且质量相差数千倍的车辆？ 这是世界物理学（地球经济）特性的体现，是对人类智力的限制吗？ 这项法律有多普遍，它将适用于其他明星的文明吗？ 全球问题。 他们不太可能在这里和现在得到解决。 但是在这里，有可能而且有必要考虑并咬一咬它会变成多少。 这就是我们要做的。

由平均体重的人举起杠铃的世界纪录^{[ 180 ]}超过200公斤。 从理论上讲，这意味着我们的身体对于至少达到Q = 2.5的冲击载荷具有安全裕度。 但是，这需要极大的力量和训练，以至于日常活动中从未使用过。 最好将糖装在50公斤的袋子中，尽管这需要装载机或助行器多四倍。 请注意，这种情况是生物进化的结果，人类的智力没有（几乎）参与其中，因此其中有一个“ alibi”。

光是物理和工程学就不能禁止高Q。 有一个用于Shuttle中途发动机的氢气涡轮增压泵，该图片右边的小东西能够产生54兆瓦的功率^{[ 60 ]} ，总车重为350公斤：

[图片来源：[ 10 ]]

如果简单地用每千克质量的功率来评估Q ，那么这比一辆体面的汽车要高100倍。 但是这东西就像火箭一样！ 制造100辆Q = 1的汽车并随其运输货物要便宜得多，而不是试图将这种设备“束缚”在轮式手推车上。

这些考虑表明，这里的原因是经济的。 而且，不是从特定经济体和国家的狭义意义上讲（因为我们的设备是由截然不同的人和系统产生的），而是从“努力的便利性”的意义上讲。 显然，这种适用性已经足够普遍，可以适用于截然不同的产品，甚至适用于动物。

_{本文是为网站https://habr.com撰写的。 复制时，请参阅来源。 本文的作者是Evgeny Bobukh 。}

让我们尝试定量研究这种权宜之计的边界。 我们提出一个问题：固定质量设备的成本如何取决于Q ？ 例如，这里有一辆重10吨的自卸车，需要10吨货物。 我们还想制造一个10吨的产品，但要带走20吨（ Q = 2）甚至50吨（ Q = 5）。 以相同的技术开发水平，相同的产量。 显然，更高的负载将增加对材料（钢->钛？），发动机（其他温度，压力）和工程（误差容限较小，设计更棘手）的要求。 显然，随着Q的增长，一切都会变得更加昂贵。 但是，与十吨相比，多少次呢？

当然，这项任务并不简单。 但是，可以从最一般的考虑中获得一些估计。 我们现在要做什么。

我们介绍函数C （ Q ）。 它描述了效率为Q的设备的最低可能成本，用Q = 1时相同质量的类似设备的成本来表示。

1.根据定义， C （1）= 1。

2. C （ Q ）是一个连续函数，至少直到质量差通过块原子测量为止。 直观地讲，具有前几个导数似乎足够平滑。 我认为我们可以（与大多数物理功能一样）承认它通常是分析性的。

3. C （ Q ）是严格增加的函数。 Q的质量越高，制造该结构就越困难，并且它的价格也就越高。 即 dC （ Q ）/ dQ > 0至少对于Q > 0。

4.当Q大于约3时， C （ Q ）开始快于线性增长。 怎么了 因为我们发现对于Q = 1的人来说，制造10吨10吨的卡车要比Q = 3的30辆卡车便宜，所以总的来说，我们写： k * C （1）< C （ k ）表示k >≈3-其他换句话说，对于k >≈3， C （ k ）的增长快于k 。

5.同样，由于Q = 0.1的十架飞机显然比Q = 1的一架飞机不经济（因为它们制造的是第二架，而不是第一架），所以对于k >≈3，我们有： k * C （1 / k ）> C （1），或C （1 / k ）> 1 / k 。

6. Shuttle的泵的成本暗示至少C = Q的值不超过Q〜100并不会随着具有重要指标的指数而增加。 否则，这个TNA不会花费数百万美元，而会花费10 ²⁰美元，而我们几乎根本不会赚。 即 C （100）在10 3-10 ^8左右 ，但不是10 ¹⁵ 。

7. C （0）等于什么？ 这就是设备的成本，该设备仍可自行移动，但无法带走任何货物。 显然，这样的“卡车”比整车便宜。 但是多少次？ 历史表明，有时而不是数十或数百。 从第一架只能自行移动（ Q = 0）的飞机到空中运输已经过去了15年，从第一架汽油车到Q = 1.5（[ 120 ] + [ 130 ]）的相当不错的卡车，还有更多。 如果这种发展是令人难以置信的复杂性，那么它几乎不可能很快完成。 因此， Q = 0的车辆的制造难度和成本不应与Q = 1的车辆完全不同。因此，我们预计C （ 0 ）约为0.1-0.5。

8.此功能对负Q有意义吗？ 挺好的！ Q = -0.5的卡车只有在从塔式起重机上卸下一半重量后才会移动。 Q = -1-这是一辆发展为零牵引力的手推车。 仅当您拖曳货物时才能够运输货物。 也就是说，通常没有引擎。 显然，它的成本，即使不是非零，也很小。 因此，将C （-1）≈0。

9. C （-2）是什么？ 这是设备的重量，必须至少拉起两倍的重量才能移动它！ 是的，区域Q <-1是锚，地基，桩，制动器。 阻碍移动的设备。 当然，这里存在完全不同的动力学及其自身的规律，但是至少我们看到C （ Q ）不会以Q <-1的奇异结尾，并且在Q = -1区域中它具有最小值，因此至少在这个点C （ Q ）的一小部分应该表现得像抛物线。

因此，粗略的C （ Q ）看起来像这样：


我们在Q = -1的点以泰勒级数展开C （ Q ）：



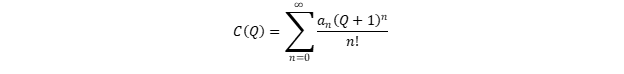
从属性（8）得出₀ =0。属性（4），（5）和部分（9）暗示₁接近于零，或者在任何情况下，其贡献都不在0范围内。 .3。

然后证明， C （ Q ）的展开中的第一个非零项是抛物线的，并且Q在单位C （ Q ）的范围内表现为近似二次函数或快速增长的函数：

C （ Q ）≈a ₂ *（ Q +1）2/2 + O（（ Q + 1 ） ³ ）

从[1]可以得出2≈1/2。

最后，由于至少直到Q〜100 ，函数C （ Q ）仍然不是指数（属性（6）），因此我们可以将其与Q ^p相等，指数p在2 ... 4范围内。 几乎没有。

结论： 在固定质量的情况下，设备C（Q）的成本增加不会弱于（Q +1）2/4，但不会快于大约O（Q ⁴ ）[1]。

是否有可能查看C （ Q ）的实际依赖性以了解此结论的正确性？ 很难 人为建立的机制大多数是不同质量的，但在统一区域内固定为Q。 我们需要相反的情况：质量大致相同，但Q不同。 起初，我希望获得有关飞机发动机的数据……但是有关其定价的工作^{[ 70 ] [ 80 ]}非常有趣。 在那里对发动机价格进行分类，并且只发布预测和平均误差的公式。

幸运的是，汽车提供了帮助^{[ 150 ]} 。 正是在他们的共同努力下，人们发现了各种容量的发动机。 尽管动力还不是可运输的货物，但经过一些工程上的努力，动力几乎与之成正比。 这使我们能够估计我们的公式是否接近现实。

好像是：

[来源：[ 150 ]]

蓝点是真正的汽车。 初步估算，它们的价格随功率密度的增加而上升，为2.3。

红点-由公式[1]计算的价格，假设Q = 1对应于每公斤20-30 000美元范围内的最便宜的汽车。 可以看出，该公式确实从下面（我们的目标位置）很好地估计了C （ Q ）。

当查看这些好吃的东西的数量时，有一个强烈的诱惑：通过它们得出C （ Q ），从而直接研究依赖关系。 无法做到这一点。 主要是因为乘用车的价格不仅取决于其牵引特性。 很难想象一辆百公斤重的汽车没有最好的空调，最舒适的座椅和“镀铑内饰的白金烟灰缸”。 所有这些花费的钱与我们的C （ Q ）无关。 但是，这里的汽车下部“分支”几乎完全按照计算出的C （ Q ）通过，看起来很有趣。 我敢承认这些只是没有多余装饰的汽车。 那里“不是跳棋，而是去”。 但是，超过10万美元的汽车价格，这些已不再存在。

_{本文是为网站https://habr.com撰写的。 复制时，请参阅来源。 本文的作者是Evgeny Bobukh 。}

因此，我们能够至少在数量级上估算具有高Q的设备的成本。 为什么有这个必要？

但是为什么。 看一下太空船的第一步。 好吧，至少是Proton-M ^{[ 110 ]} ，以确保具体性。 她是一辆几乎成熟的汽车，配有发动机，控制系统，相当不错的安全性和31吨的干重。 同时，在火箭发动时，它不仅使有效载荷而且对所有燃料，所有上层级，当然还有其自身都起拖曳作用。 总计-683吨。 加上启动过载，总计（有效）1068吨负载！ 从 第一阶段 的角度 来看，它工作在可怕的模式下Q =（1068/31）= 34.4！ 这相当于在客车上堆放50吨货物。

而且我们知道，具有高Q的设备的成本至少是（Q + 1）的2/4倍，而与Q≈1类似。对于质子，这等于... 313倍。

也就是说，质子的价格应该是Q = 1的同类设备的300倍。而且，这个数字几乎不依赖于进展和技术。 因为“英国科学家”发明了一种使火箭便宜的超级合金，所以地面发动机也变得便宜了。 因此，即使是可重复使用的化学火箭也总是很昂贵的。 喜欢与否。

好啊 假设有300次。 但是与什么相比呢 ？ 将我们的计算结果与一些客观存在的设备进行比较以消除总误差会很好吗？

不幸的是，没有30吨Q = 1的导弹。 但是，有一些适合进行比较的近似类似物：

• 首先是矿用卡车。 是的，不是火箭。 但它仍然是热机，不是完全琐碎的工程，也是最便宜的货物运输方式之一。 如果我们已经在谈论太空探索，那么卡车是否不应该成为太空驾驶室商业模式的原型？ 因此，让我们尝试一下，至少要进行一般的估算。 这是一吨30吨的Belaz-7540。 市场价格^{[ 140 ]}为370万卢布，即 $ 62K。 对于Proton，这将转换为第一阶段的费用1900万美元。 维基百科表示^{[ 100 ]的}启动费用为6500万美元。 非常接近，因为除了第一步的价格外，这还包括更多。
• 在[ 160 ]中，描述了在轨道上的实验火箭平台。 10吨的质量（五个步骤）加速到4 km / s。 价格是750公斤。 从发布的图片和参数来看，该设备的工作效率为Q =10。不是一个单位，但仍然不是34。如果从这些数字开始，质子的第一步应该花费2300万美元。
• 通常，当我尝试想象Q = 1的火箭时，在我的脑海中会出现一种巨大的毛坯，上面有一个充满火药的小缺口。 火药燃烧，将坯料向前推。 一点点，您都不会加速。 我把这张照片拖了两天，直到我意识到它让我想起。 这是...气动锤！ 气体膨胀并推动毛坯的位置。 喷气发动机概念的终极混蛋，仍然保留着某种血缘关系。 好吧，我们正在寻找。 是的，这是^{[ 170 ]} Stanko M212气动锤。 圆盘的重量为2吨，整体结构为58.3吨。 因此， Q系统为适度的0.034。 售价4万欧元。 如果根据公式[1]将这个笑话的成本推算为Q = 34.4，我们将得到... 4,700万欧元。 或超过30吨的比例为2400万。

看来我们并没有真正脱离现实。

总结一下。 由于火箭甚至是可重复使用的火箭，其价格都比卡车贵2–3个数量级，因此，由地面材料制成的任何空间解决方案的成本也将比地面同类产品高100–1,000倍。 这是发展的很高的障碍。

导弹之所以昂贵，是因为它们很重，并且在高Q条件下不健康时会被迫工作。 但是，为什么火箭很重？ 我们将在第二部分中考虑答案（比Tsiolkovsky公式要深一些）。

待续 。

更新：一些人在考虑导弹时试图指出关于燃料的含糊之处。 我考虑过了 我意识到文章中确实存在一些错误。 在这里查看评论。