估计空间方向，或者如何不惧怕Mahoney和Majwik过滤器

我们在说什么

在Habre上出现有关Majwik过滤器的帖子是其自身的象征性事件。 显然，对无人机的普遍热情重新激发了人们对通过惯性测量来评估人体方位的兴趣。 同时，基于卡尔曼滤波器的传统方法不再满足公众的要求-要么是由于对无人机无法接受的计算资源的高要求，要么是因为设置复杂且不直观。

该职位伴随着一个非常紧凑和高效的C过滤器实现。但是，从注释来看，此代码的物理含义以及整篇文章对于某人来说仍然很模糊。 好吧，我们坦率地承认：Majwik过滤器是基于非常简单而优雅的原则的最复杂的过滤器组。 我将在我的文章中考虑这些原则。 代码将不在这里。 我的帖子不是关于定向估计算法的特定实现的故事，而是关于在给定主题上发明自己的变体的邀请，这可能很多。

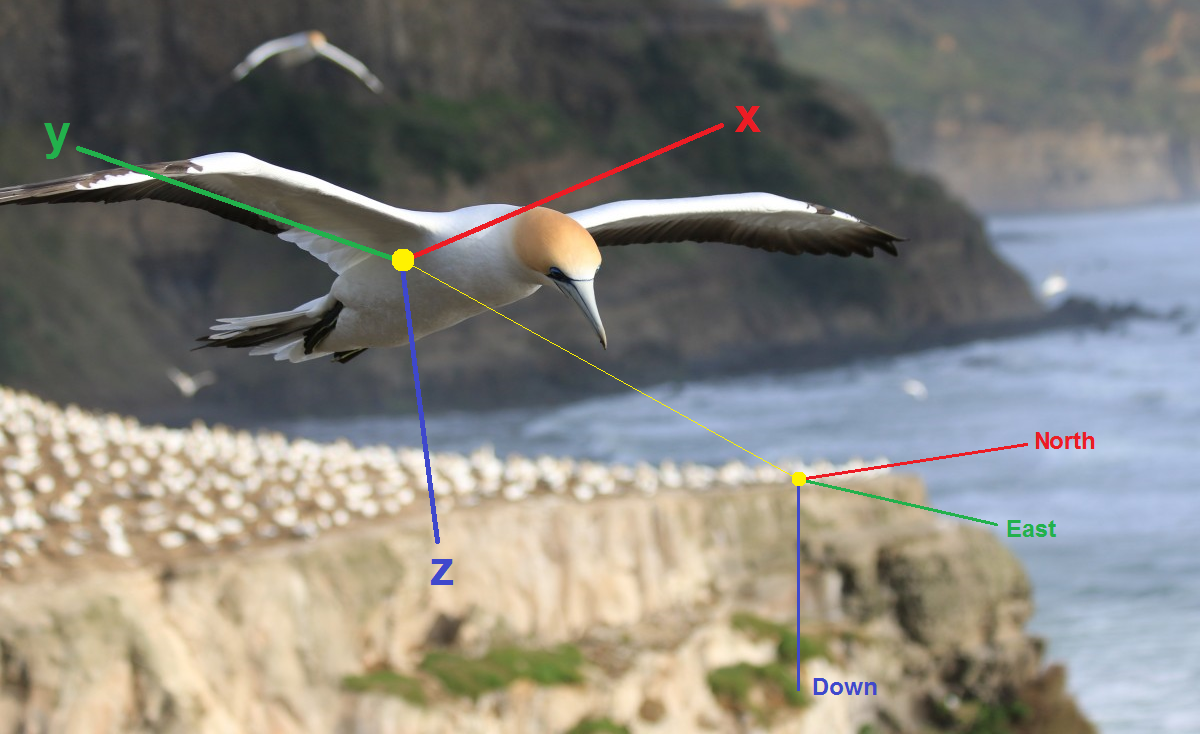
方向视图

回顾基础知识。 要评估身体在空​​间中的方向，首先需要选择一些参数，这些参数共同唯一地确定该方向，即 本质上是相关坐标系的方向 $$$xyz$ 相对有条件的固定系统-例如，地理系统NED（北，东，下）。 然后您需要制作运动方程，即 通过陀螺仪的角速度表达这些参数的变化率。 最后，需要将来自加速度计，磁力计等的矢量测量值引入计算中。 以下是表示方向的最常见方法：

欧拉角 -卷（roll， $$$\ phi$ ），音高（pitch， $$$\ theta$ ），课程（标题， $$$\ psi$ ） 这是最直观，最简洁的定向参数集：参数的数量恰好等于旋转自由度的数量。 对于这些角度，我们可以写出欧拉运动方程 。 他们非常喜欢理论力学，但是在导航问题上却很少使用。 首先，知道角度不允许直接将任何矢量的分量从相连的坐标系转换到地理坐标系，反之亦然。 其次，在±90度的螺距下，运动方程退化，侧倾和横倾变得不确定。

旋转矩阵 -矩阵 $$$\ mathbf {C}$ 3×3大小，您需要将其乘以关联坐标系中的任何向量，以在地理系统中获得相同的向量： $$$\ mathbf {r} _ {NED} = \ mathbf {C} \ mathbf {r} _ {xyz}$ 。 矩阵始终是正交的，即 $$$\ mathbf {C} = \ mathbf {C} ^ {T}$ 。 运动学方程的形式为 $$$\点{\ mathbf {C}} = \ mathbf {C} \ mathbf {\ Omega}$ 。
在这里 $$$\ mathbf {\ Omega}$ -由陀螺仪在连接的坐标系中测量的角速度分量矩阵：

$$

$$\ mathbf {\ Omega} = \开始{bmatrix} 0＆-\ omega_ {z}＆\ omega_ {y} \\ \ omega_ {z}＆0＆--\ omega_ {x} \\-\ omega_ {y }＆\ omega_ {x}＆0 \\ \ end {bmatrix}$$

旋转矩阵不如欧拉角明显，但是与它们不同，它允许您直接转换向量，并且在任何角度位置都不会失去意义。 从计算的角度来看，它的主要缺点是冗余：为了实现三个自由度，一次引入了九个参数，所有这些参数都需要根据运动方程进行更新。 通过使用矩阵的正交性可以稍微简化该问题。

旋转四元数是一种针对冗余和退化的激进但非常不直观的补救措施。 这是一个四个组成部分的对象。 $$$\ mathbf {q} = q_ {0} + q_ {1} \ mathbf {i} + q_ {2} \ mathbf {j} + q_ {3} \ mathbf {k}$ -不是数字，不是向量，也不是矩阵。 四元数可以从两个角度查看。 首先，标量的形式量如何 $$$q_ {0}$ 和向量 $$$q_ {1} \ mathbf {i} + q_ {2} \ mathbf {j} + q_ {3} \ mathbf {k}$ 在哪里 $$$\ mathbf {i}，\ mathbf {j}，\ mathbf {k}$ -单位轴向量（当然听起来很荒谬）。 其次，作为复数的概括，现在我们不使用一个，而是使用三个不同的虚构单位 $$$\ mathbf {i}，\ mathbf {j}，\ mathbf {k}$ （听起来同样荒唐）。 四元数与转弯有何关系？ 通过欧拉定理：始终可以通过一定角度的有限旋转将物体从一种给定的方向转移到另一种方向 $$$\ alpha$ 围绕某个轴并带有引导向量 $$$\ mathbf {u}$ 。 这些角度和轴可以组合成四元数： $$$\ mathbf {q} = \ mathrm {cos}（\ alpha / 2）+ \ mathbf {u} \ mathrm {sin}（\ alpha / 2）$ 。 像矩阵一样，四元数可用于直接将任何矢量从一个坐标系转换为另一个坐标系： $$$\ mathbf {r} _ {NED} = \ mathbf {q} \ mathbf {r} _ {xyz} {\ mathbf {q}} ^ {-1}$ 。 如您所见，方向的四元数表示形式也存在冗余，但比矩阵少得多：额外的参数仅为一个。 对四元数的全面审查已经在哈布雷（Habré）上进行 。 他们讨论了几何和3D图形。 我们也对运动学感兴趣，因为四元数的变化率必须与测得的角速度有关。 相应的运动方程式为 $$$\点{\ mathbf {q}} = 1/2 \ mathbf {q} \ mathbf {\ omega}$ 向量在哪里 $$$\ mathbf {\ omega}$ 也被认为是标量为零的四元数。

筛选方案

最简单的计算方向的方法是用运动学方程式武装自己，并根据它更新我们喜欢的任何参数集。 例如，如果我们选择一个旋转矩阵，则可以按照C += * Omega * dt的精神编写一个循环。 结果将令人失望。 陀螺仪，尤其是MEMS，具有较大且不稳定的零偏移-结果，即使在完全静止的情况下，计算出的方向也将具有无限的累积误差（漂移）。 Mahoney，Majwick和许多其他人（不排除我）发明的所有技巧旨在通过涉及来自加速度计，磁力计，GNSS接收器，滞后等的测量来补偿这种漂移。 因此，基于简单的基本原理，定向过滤器的整个家族诞生了。

基本原理。 为了补偿方向漂移，有必要在陀螺仪测量的角速度上增加一个基于其他传感器的矢量测量构造的附加控制角速度。 控制角速度矢量应努力将测量矢量的方向与其已知的真实方向组合在一起。

与构造卡尔曼滤波器的校正项相比，此处采用了完全不同的方法。 主要区别在于控制角速度不是项，而是估计值（矩阵或四元数）的一个因素 。 重要的优点是：

• 可以针对方向本身构建评估过滤器，而不是针对方向与陀螺仪提供的方向有小的偏差。 此外，估计值将自动满足任务施加的所有要求：矩阵将正交，四元数被归一化。
• 控制角速度的物理含义比卡尔曼滤波器中的校正项更加清楚。 所有操作都是在普通的三维物理空间中，而不是在抽象的多维状态空间中，通过向量和矩阵完成的。 这极大地简化了过滤器的优化和调整，此外，它还使您摆脱了大尺寸矩阵和重矩阵库。

现在，让我们看看如何在特定的过滤器选项中实现此想法。

Mahoney过滤器。 最初的Mahoney文章中所有的愤怒数学都是为了证明简单方程式而写的（32）。 我们用符号重写它们。 如果我们忽略对陀螺仪零位移的估计，则剩下两个关键方程-旋转矩阵本身的运动学方程（控制角速度采用矩阵形式 $$$\ mathbf {\ Omega}'$ ）以及向量形式的速度形成规律 $$$\ mathbf {\ omega}'$ 。 为简单起见，我们假设没有加速度或磁头，因此，我们可以使用自由落体加速度测量。 $$$-\帽子{\ mathbf {g}} _ {xyz}$ 来自加速度计和地球磁场 $$$\帽子{\ mathbf {m}} _ {xyz}$ 从磁力计。 这两个向量均由连接坐标系中的传感器测量，并且在地理系统中其位置已知： $$$-\ mathbf {g} _ {NED}$ 朝上 $$$\ mathbf {m} _ {NED}$ -到磁北。 然后，Mahoney滤波器方程将如下所示：

$$

$$\点{\ mathbf {C}} = \ mathbf {C}（\ mathbf {\ Omega} + \ mathbf {\ Omega}'）\\ \ mathbf {\ omega'} = k_ {g} \帽子{\ mathbf {g}} _ {xyz} \ times \ mathbf {C} ^ {T} \ mathbf {g} _ {NED} + k_ {m} \ hat {\ mathbf {m}} _ {xyz} \ times \ mathbf {C} ^ {T} \ mathbf {m} _ {NED}$$

让我们仔细看第二个方程。 右边的第一项是向量积。 第一个因素是测得的重力加速度，第二个因素是正确的。 由于这些因子必须在一个坐标系中，因此第二个因子可以通过乘以 $$$\ mathbf {C} ^ {T}$ 。 构造为矢量积的角速度垂直于因子矢量的平面。 它允许您旋转关联坐标系的估计位置，直到因子向量的方向一致-然后向量乘积将重置为零，并且旋转将停止。 系数 $$$k_ {g}$ 设置此类反馈的刚性。 第二项对磁矢量执行类似的运算。 实际上，Mahoney滤波器体现了众所周知的论点：两个不同坐标系中两个非共线矢量的知识使您可以唯一地恢复这些系统的相互定向。 如果向量多于两个，则这将提供有用的测量冗余。 如果只有一个矢量，则不能固定一个旋转自由度（围绕该矢量的运动）。 例如，如果仅给出一个向量 $$$-\ mathbf {g}$ ，则可以调整侧倾和俯仰的漂移，但不能调整航向。

当然，Mahoney滤波器不必使用旋转矩阵。 也有非规范的四元数变体。

虚拟陀螺仪平台。 在Mahoney滤波器中，我们应用了控制角速度 $$$\ mathbf {\ omega'}$ 到相关的坐标系。 但是您可以将其应用于地理坐标系的估计位置。 运动方程式为

$$

$$\点{\ mathbf {C}} = \ mathbf {C} \ mathbf {\ Omega}-\ mathbf {\ Omega}'\ mathbf {C}$$

事实证明，这种方法为非常丰富的物理类比铺平了道路。 只要回想一下陀螺仪技术的初衷-基于万向节中陀螺仪稳定平台的垂直和惯性导航系统即可。


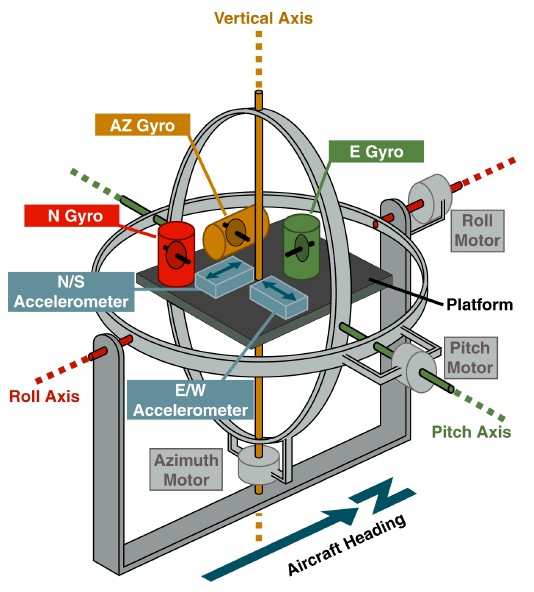www.theairlinepilots.com

该平台的目标是实现地理坐标系。 通过悬架上的角度传感器相对于该平台测量载体的方​​向。 如果陀螺仪有漂移，则平台也会随之漂移，并且角度传感器的读数中会累积误差。 为了消除这些错误，从平台上安装的加速度计引入了反馈。 例如，平台相对于北轴的地平线的偏离是通过东轴的加速度计来感知的。 该信号允许设置控制角速度 $$$\ mathbf {\ omega'}$ 使平台回到地平线。

我们可以在任务中使用相同的视觉概念。 然后，必须将所描述的运动方程式理解为：方向变化率是两个旋转运动之间的差值-载体的绝对运动（第一项）和虚拟陀螺仪平台的绝对运动（第二项）。 该类比可以扩展到控制角速度的形成定律。 向量 $$$-\ hat {\ mathbf {g}} _ {NED} =-\ mathbf {C} \ hat {\ mathbf {g}} _ {xyz}$ 它代表了加速度计的证词，据说是站在陀螺仪平台上的。 然后，出于物理原因，您可以编写：

$$

$$\ omega'_ {N} =-gk_ {g} \帽子{g} _ {E}，\; \ omega'_ {E} = gk_ {g} \帽子{g} _ {N}$$

通过按照Mahoney滤波器的精神进行矢量乘法，可以以正式的方式获得完全相同的结果，但现在不是在相连的坐标系中，而是在地理坐标系中。 仅需要吗？

显然，在古老的波音公司专利中出现了平台惯性导航与捷联惯性导航之间有用的类比的第一个提示。 后来，这个想法由萨利切夫（Salychev ）积极地提出 ，最近也由我提出 。 这种方法的明显优势：

• 可以基于可理解的物理原理来形成控制角速度。
• 自然，水平通道和方向通道的属性和校正方法有很大不同，它们是分开的。 在Mahoney过滤器中，它们是混合的。
• 使用GNSS数据可以很方便地补偿加速度的影响，这些数据是在地理轴而不是在相关轴中精确发布的。
• 在需要考虑地球的形状和旋转的高精度惯性导航的情况下，很容易将算法推广。 我无法想象在Mahoney方案中如何做到这一点。

Majwick过滤器。 Majwik选择了艰难的道路 。 显然，如果Mahoney凭直觉做出决定，然后在数学上证明其合理性，那么Majwik从一开始就证明自己是形式主义者。 他承诺解决优化问题。 他这样推理。 设置旋转四元数的方向。 在理想情况下，某些测量矢量的计算方向（让我们知道 $$$-\ mathbf {g}$ ）与真实值一致。 然后将 $$${\ mathbf {q}} ^ {-1} \ mathbf {g} _ {NED} \ mathbf {q} = \ hat {\ mathbf {g}} _ {xyz}$ 。 实际上，这并非总是可以实现的（特别是如果有两个以上的向量），但是您可以尝试使偏差最小化 $$$\ mathbf {F} = {\ mathbf {q} ^ {-1} \ mathbf {g} _ {NED} \ mathbf {q}}-\ hat {\ mathbf {g}} _ {xyz}$ 从完全平等。 为此，我们引入了最小化准则

$$

$$E = \ frac {1} {2} | \ mathbf {F} | ^ {2} \ rightarrow \ mathrm {min}$$

最小化需要梯度下降-在与梯度相反的方向上以小步长移动 $$$\ nabla E$ ，即 与功能最快的增长相反 $$$E$ 。 顺便说一句，Majwik犯了一个错误：他在所有作品中都没有介绍 $$$E$ 并坚持写 $$$\ nabla \ mathbf {F}$ 代替 $$$\ nabla E$ ，尽管实际上可以准确计算 $$$\ nabla E$ 。

结果，梯度下降导致以下条件：为了补偿方向漂移，必须从运动方程中添加一个与运动方程成比例的新负项。 $$$\ nabla E$ ：

$$

$$\ dot {\ mathbf {q}} = \ frac {1} {2} \ mathbf {q} \ mathbf {\ omega}-\ beta \ frac {\ nabla E} {| \ nabla E |}$$

在此，Majwik与我们的“基本原理”略有不同：他没有将校正项添加到角速度，而是添加了四元数的变化率，这并不完全相同。 结果，可能会导致更新的四元数不再是单个四元数，因此失去了表示方向的能力。 因此，对于Majwik滤镜，四元数的人工归一化是至关重要的操作，而对于其他滤镜而言，则是不可取的。

加速的影响

到现在为止，一直没有真正的加速度，加速度计只能测量重力加速度 $$$-\ mathbf {g}$ 。 这使得获得垂直标准成为可能，并在其帮助下补偿侧倾和俯仰漂移。 但是，在一般情况下，加速度计无论其工作原理如何，都可以测量视在加速度 -真实加速度和重力加速度的矢量差 $$$\ mathbf {f} = \ mathbf {a}-\ mathbf {g}$ 。 视在加速度的方向与垂直方向不一致，并且由加速度引起的误差会出现在侧倾和俯仰估计中。

使用虚拟陀螺仪平台的类比很容易说明。 她的校正系统的设计使平台停止在该角度位置，在该角度位置，假定安装在其上的加速度计信号被重置为零，即 当测得的向量 $$$\ mathbf {f}$ 变得垂直于加速度计的灵敏度轴。 如果没有加速度，则该位置与地平线重合。 当发生水平加速度时，陀螺仪平台会偏转。 可以说，陀螺仪平台类似于强阻尼的摆线或铅垂线。



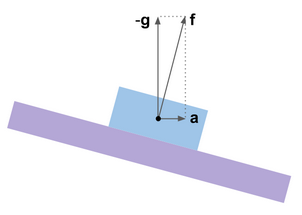
在有关Majwik过滤器的帖子评论中，出现了一个问题，即是否可以希望该过滤器比Mahoney过滤器更不容易受到加速度的影响。 las，这里描述的所有过滤器都利用相同的物理原理，因此遭受相同的问题。 用数学欺骗物理学是不可能的。 那该怎么办？

最简单，最困难的方法是上世纪90年代中期发明的航空陀螺垂直系统：在存在加速度或航向角速度（表示进入转弯）的情况下，将控制角速度减小或完全为零。 可以将相同的方法应用于当前平台系统。 在这种情况下，必须通过以下值来判断加速度 $$$\ hat {f} _ {N}，\ hat {f} _ {E}$ 但不是 $$$\ hat {f} _ {x}，\ hat {f} _ {y}$ 本身就是零。 但是大小 $$$\帽子{\ mathbf {f}} _ {NED}$ 由于陀螺仪平台的倾斜度必须消除，因此并非总是能够将真实加速度与重力加速度的投影区分开。 因此，该方法无法可靠地工作-但不需要任何其他传感器。

一种更准确的方法是基于使用GNSS接收器的外部速度测量值。 如果知道速度 $$$\ mathbf {v}$ ，则可以对其进行数值微分并获得真实的加速度 $$$\点{\ mathbf {v}}$ 。 那么区别 $$$\ hat {\ mathbf {f}} _ {NED}-\点{\ mathbf {v}}$ 将完全相等 $$$-\帽子{\ mathbf {g}} _ {NED}$ 不管媒体的动向。 可以用作垂直的标准。 例如，您可以以以下形式指定陀螺仪平台的控制角速度

$$

$$\ omega'_ {N} = gk_ {g}（\ hat {f} _ {E}-\ dot {v} _ {E}），\; \ omega'_ {E} =-gk_ {g}（\帽子{f} _ {N}-\点{v} _ {N}）$$

传感器零偏移

消费级陀螺仪和加速度计的一个令人遗憾的功能是时间和温度零偏移的巨大不稳定性。 要消除它们，仅在工厂或实验室进行校准是不够的-您需要在操作期间进行重新评估。

陀螺仪。 我们将处理陀螺仪的零偏移 $$$\ delta {\ mathbf {\ omega}}$ 。 关联坐标系的估计位置偏离其真实位置的角速度由两个相反的因素确定-陀螺仪的零位移和控制角速度： $$$\ delta {\ mathbf {\ omega}}-\ mathbf {\ omega'}$ 。 如果更正系统（例如，在Mahoney过滤器中）设法停止了出口，那么在稳定状态下它将 $$$\ delta {\ mathbf {\ omega}} = \ mathbf {\ omega'}$ 。 换句话说，在控制角速度 $$$\ mathbf {\ omega'}$ 有关未知有效扰动的信息 $$$\ delta {\ mathbf {\ omega}}$ 。 因此，可以应用补偿估计 ：我们不直接知道扰动的大小，但是，我们知道需要采取什么纠正措施来平衡它。 这是估算陀螺仪零位移的基础。 例如，在Mahoney中，分数会根据法律进行更新

$$

$$\ dot {\ hat {\ delta \ mathbf {\ omega}}} = k_ {b} \ mathbf {\ omega'}$$

但是，结果却很奇怪：估计达到0.04 rad / s。 即使在最讨厌的陀螺仪中，零偏移的这种不稳定性也不会发生。 我怀疑问题是Mahoney不使用GNSS或其他外部传感器-并完全受到加速度的影响。 仅在不损害加速度的垂直轴上，估计值看起来或多或少是可靠的：


Mahony等，2008

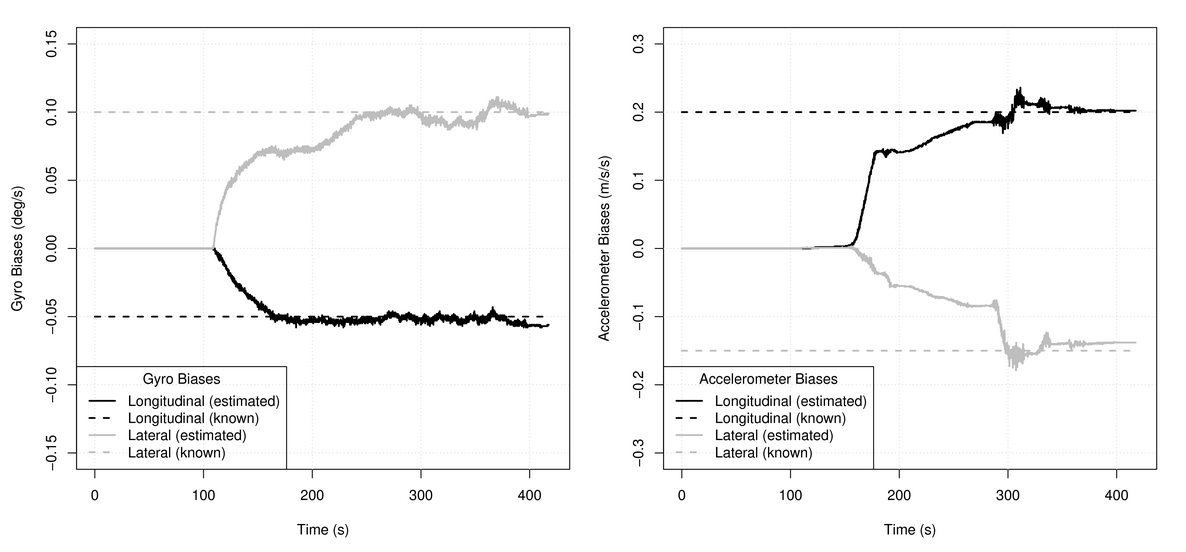
加速度计 零偏移加速度传感器 $$$\ delta {\ mathbf {f}}$ 更难。 必须从相同的控制角速度中提取有关它们的信息 $$$\ mathbf {\ omega'}$ 。 但是，在直线运动中，加速度计零位移的影响与支架的倾斜度或传感器块在其上的安装歪斜没有区别。 没有添加剂 $$$\ mathbf {\ omega'}$ 加速度计不会创建。 添加剂仅转一圈出现，这使我们能够分离并独立地评估陀螺仪和加速度计的误差。 我的文章中提供了一个有关如何完成此操作的示例。 这是那里的照片：

而不是得出结论：卡尔曼滤波器如何？

我毫不怀疑，这里描述的过滤器在速度，代码紧凑性和易于设置方面几乎总是比传统的Kalman过滤器具有优势-为此，它们是创建的。 至于评估的准确性，这里还不是很清楚。 我遇到了设计不成功的卡尔曼滤波器，其精度明显不及带有虚拟陀螺仪平台的滤波器。 Majwik还证明了相对于一些 Kalman估计，他的滤波器的好处。 但是，对于相同的方位估计任务，您可以至少构建十二个不同的卡尔曼滤波器电路，每个电路都有无数的设置。 我没有理由认为Mahoney或Majwik滤波器会比可能的最佳 Kalman滤波器更准确。 当然，卡尔曼方法将始终具有通用性的优点：它不会对评估系统的特定动态特性施加任何严格的限制。