第2部分。非常重的燃料
上一部分1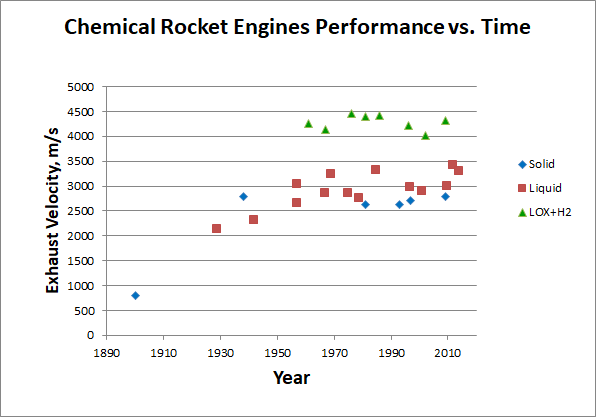
在您之前是国际空间站。 质量为420吨,价值
[ 20 ]为1500亿美元:

她的动能是旧的
E =
mv 2/2 ,为1.3 * 10
13焦耳。 在400公里的高度加上势能,我们得到1.4 * 10
13J 。
您需要燃烧多少天然气才能获得这种能量? 事实证明不是那么多。 总计350吨。 这大约是乌兰乌德
[ 200 ]的一日能源预算。
一天之内离世界上最富裕的城市有多远,它管理着足够的能量使ISS加速进入轨道速度,但是,我们在整个世界上只有一个站点,并且花费了不菲的疯狂金钱?
答案
在于从运载火箭的解剖学上可以明显看出。
承运人至少必须包括:
- 有效负载。 否则,为什么需要它呢?
- 至少一个引擎。
- 连接所有这些的外壳。
- 而且,当然是燃料。 作为一种工作流体,在大多数情况下,作为一种能源。
在最后一段中,问题是根源。 要提高和拖动一定量的最低燃料,您需要……正确地,需要额外的燃料! 在上升的同时,您还需要加油! 而且这种包装可以持续很长时间。 当然,它会收敛,否则我们将不会飞到任何地方。 但是,根据融合的结果,现代火箭,甚至是多级甚至高质量的设计和执行,其质量都主要由这种燃料组成。
好吧,这是一个教科书的例子,土星V不是最新的,而是历史上最有效的导弹之一
[ 30 ] :

[来自NASA历史的原始图片[
40 ]]
起始重量-2970吨。 其中约有2670种是燃料。 在整个月球探险不到三分钟的时间里,其中2160枚被烧毁。 尽管事实上,有效载荷在轨道上的动能仅“消耗”了100吨燃料。
事实证明,进入轨道的主要困难不是缺乏能量。 她的地球人不仅具有足够的动能,而且不仅对于车站而言,甚至对于在轨游轮也具有足够的动能。 问题不同:我们的燃料太重了。 要收集飞行所需的能量,需要太多以千克为单位的能量。 为什么大多数注入到火箭中的燃料将用于燃料运输。 实际上,Tsiolkovsky公式将火箭的起始
M和最终质量
m与速度
V和发动机的排气速度联系起来,这告诉了我们一件事:
M /
m = e
V / u [2]
乍一看,还不完全清楚每公斤的能量含量与它有什么关系? 但是,一切都很简单。 它以到期时间“坐”在
u中。 对于化学燃料,它受
u =√(2
q )的限制(且等于1的第一近似值),其中
q是燃烧的比热。 这是每公斤的能量含量。 当这个
q “不足”时,开始和结束时的质量比就会成倍增长:
M /
m = e
V /√(2 q ) [3]
或
V = Ln(
M /
m )*√(
2q )[3a]
一些书呆子和澄清的注意事项1.是的,流量的表达式比
u =√(
2q )更精确。 当我为他们获得荣誉时,戈尔巴乔夫“移交”了苏联。 但是这些公式很复杂,吓scar读者,并考虑了在这里不重要的影响。
u =√(
2q ),尽管它高估了答案10-30%,但足以描述我们对利益的依赖。 是的,有一种特定的冲动,但在这篇特定文章中,流速更易于使用。
2.原则上,即使化学火箭也没有禁止其获得高于√(2
q )的流出速度
u的条件 。 怎么了 好吧,让我们说,不是在喷嘴中而是在发电机中燃烧燃料,从而产生电能。 然后,利用这种能量
将排气的分数
x (0 <
x≤1 )加速到非常高的速度。 例如,等离子电动喷气发动机
[ 230 ] 。 废气残留物以零速度愚蠢地倾倒。 为简单起见,我们假定所有转换都没有能量损失,效率为100%。 这样的火箭会否以固定的质量比
M /
m加速到更高的速度
V (即会更有效)吗?
答案是否定的。 求解描述此类火箭运动的方程式很容易,并获得:
V = Ln(
M /
m )*√(
2qx )
即 它的最终速度仅为带有直接燃料燃烧的“普通”火箭的√x(参见[3a])。 而且这个速度仍然严格地与
q相关 。
3.如果火箭不依靠燃料而是依靠电池,该怎么办? 好吧,让船上有一个单独的质量为
m f的工作介质,以及一个分别具有储能
E和质量
m b的电池。
您首先需要了解的是,电池必须包含许多小的“模块”,这些模块在工作时会被重置。 否则,我们将随身携带空电池的“死”负载。 但是如果是这样,那么从概念上讲,这与船上具有总能量储备
E和质量
m f +
m b的普通燃料没有什么不同。 而且如果这种系统的
q =
E /(
m f +
m b )低于常规化学火箭的话,它将无法更好地飞行。
5.但是电动火箭发动机
[ 225 ]呢? 毕竟,它们的流速高达每秒数十千米和数百千米,并且它们以非常适中的
M /
m比率执行了成功的行星际机动。 怎么会这样 事实是ERD是开放系统。 它们携带工作液(汞,氙气等)。 但是能量不是。 能源来自太阳能电池板。 相反,如果它们携带能量质量为
q的普通电池,则根据公式[3a],其效率不会更高。
本文是为网站https://habr.com撰写的。 复制时,请参阅来源。 本文的作者是Evgeny Bobukh 。因此,导弹之所以昂贵,是因为其极其轻巧的“干式”设计被迫承受非常重的负载,其中大部分是燃料(甚至可以通过TNA快速“泵送”)。 而且负荷很大,因为我们的燃料太重
了 。 每公斤焦耳几乎没有放置。
现在让我们了解这种限制的原因。
为什么要仔细研究氢在氟中的燃烧反应,这是最简单的反应之一。 在其中,氢-氢和氟-氟对交换伙伴,形成两个氢-氟对:
H 2 +
F 2 = 2
HF释放的能量从哪里来?
氢分子具有两个原子。 原子有电子。 它们以一种云的形式“涂抹”在原子周围,并且主要通过静电吸引与原子核连接。 电子是外部,化合价和(氢除外)内部的电子,不参与化学反应。 反应后,氢和氟发生变化。 价电子的电子云会重新分布,并略微改变其形状。 像这样:
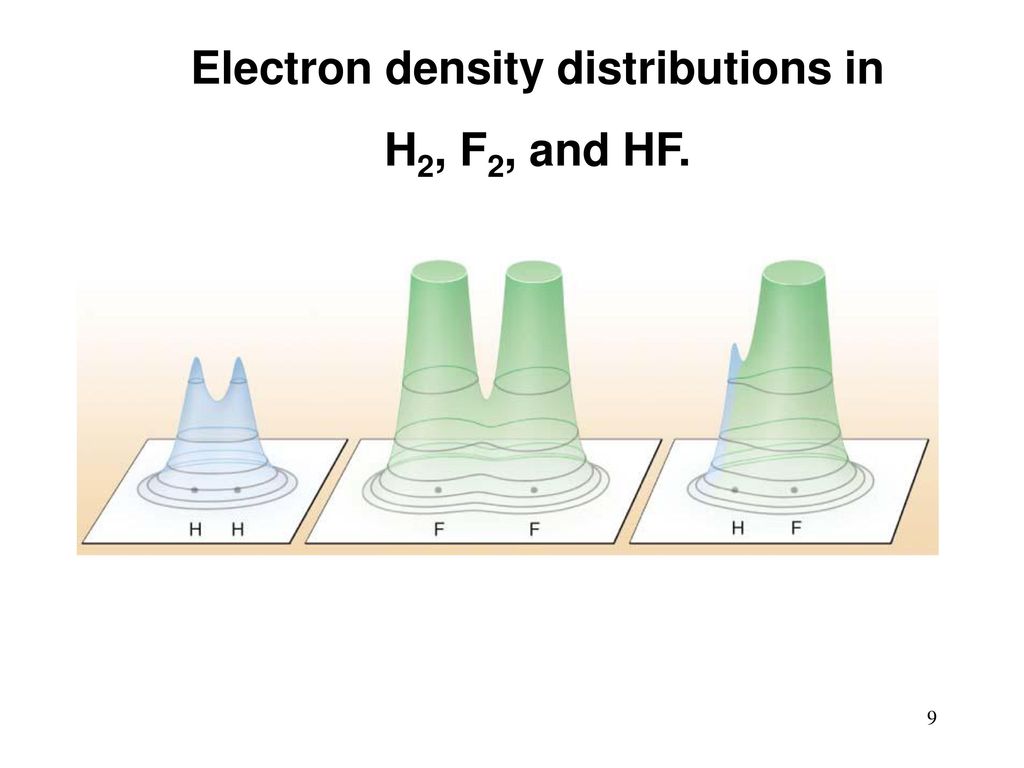
[图像学分[
295 ]]
电子与新云中原子的潜在结合能不同。 在这种情况下(该能量为负),现在分别小于
H 2和
F 2 。 差异在哪里? 分子的动能,原子的振动,电磁辐射。 所有这些最终变成了热量。 气体膨胀并产生牵引力。
这是关键时刻。 只有外部价电子参与化学反应。 其他电子的密度分布(以及原子“深度”内的电场)实际上保持不变。 在化学反应中,原子像通过价电子那样的“中间物”彼此相互作用:
现在,注意的问题是:在这种“置换”过程中可以释放的最大能量是多少? 显然,它不能超过外部电子与原子的结合能之和(在最终和初始产物中)。 但是这些结合能是我们众所周知的
[ 285 ] 。 每一个原子,它们等于1.5-25
电子伏特 (
eV ),用Rydberg常数的分数表示。Rydberg常数是由我们的宇宙基本常数构成的基本值:
Ry (在高斯系统中)=
m e e 4/2 2 =
1 3 .6 eV [
300 ]
此外,25和13.6 eV均无法获得。 因为在典型的反应中,结合能几乎没有释放出来,但是只有两种构型之间的结合能才释放出来,因此化学能释放的实际上限是每个原子3-4 eV。 以典型的燃料+氧化剂千克计,这相当于释放20-30 MJ的能量。 正是这个数量设置了直接燃烧的化学喷气发动机的理论最大气体速度
u =√(2
q )=√(2 * 2.5 * 10
7 )≈7000 m / s。 当然是无法实现的,因为它没有考虑分子内部自由度,解离,辐射,无方向热运动等方面的损失。
表格形式的燃烧热
[ 240 ] (例如,氢为120 MJ / kg)似乎与上面的数字相矛盾。 但是事实是,这些热量通常以每千克
燃料为单位显示,而没有考虑其燃烧所需的氧化剂。 火箭同时带有两个成分,如果我们重新计算每千克
混合物释放的能量(平衡燃烧),就会出现完全不同的情况
[ 240 ] [ 250 ] [ 260 ] :
| 燃料+氧化剂 | 反应 | 每公斤的热值。 燃料,MJ / kg | 1公斤燃料需要氧化剂,kg。 | 热值,MJ / kg | 混合物每个原子的输出,eV |
| 氢+氧 | 2H 2 + O 2 = 2H 2 O | 120 | 8 | 13.3 | 0.83 |
| 煤油+氧气 | 2C 12 H 26 + 37O 2 = 24CO 2 + 26H 2 O | 43 | 3.5 | 9.6 | 1.02 |
| 煤+氧气 | C + O 2 = CO 2 | 33 | 2.7 | 9.0 | 1.38 |
| 锂+氧 | 4Li + O 2 = 2Li 2 O | 43.5 | 1.2 | 20.2 | 2.10 |
| 硼+氧 | 2B + 1.5O 2 = B 2 O 3 | 57.2 | 2.2 | 17.8 | 2.58 |
| 镁+氧 | 2Mg + O 2 = 2MgO | 25.1 | 0.7 | 15.1 | 3.18 |
| 铍+氧气 | 2Be + O 2 = 2BeO | 66.6 | 1.8 | 24.0 | 3.12 |
| 锂+氟 | 2Li + F 2 = 2LiF | 88.8 | 2.7 | 23.7 | 3.21 |
| 铍+氟化物 | Be + F 2 = BeF 2 | 114 | 4.2 | 21.9 | 3.57 |
| 双氰基乙炔+臭氧 | C 4 N 2 +(4/3)O 3 = 4CO + N 2 | 16.2 | 0.8 | 8.8 | 1.28 |
如您所见,即使是最耗能的能源,尽管不适合实际使用,燃料在燃烧过程中也仅产生24 MJ / kg的热量。 而且,我们几乎从航天学开始就遇到了这个限制,它显示了化学发动机的流出速度图表,取决于其制造年份:

[根据[
310 ],[
320 ],[
330 ]的早期引擎,后来-维基百科。
这里的数据收集]
看来化学燃料的潜力已被长期开发。 是否可以开始以其他形式存储能量?
待续。