从头开始编写XGBoost-第1部分：决策树

哈Ha！

在大量搜索有关决策树和集成算法（增强，决策森林等）的高质量指南之后，这些指南以编程语言直接实现，并且没有发现任何内容（无论找到任何内容，在注释中写下这些内容，也许我会学到新知识），我决定自己领导，正如我希望看到的那样。 文字上的任务很简单，但是，正如您所知，魔鬼在细节中，其中有很多使用树的算法。

由于该主题涉及面很广，因此很难将所有内容放到一篇文章中，因此将有两篇出版物：第一篇专门讨论树木，第二篇专门讨论梯度提升算法的实现。 此处介绍的所有材料都是基于开源，我的代码，同事和朋友的代码进行编译和设计的。 我立即警告您，会有很多代码。



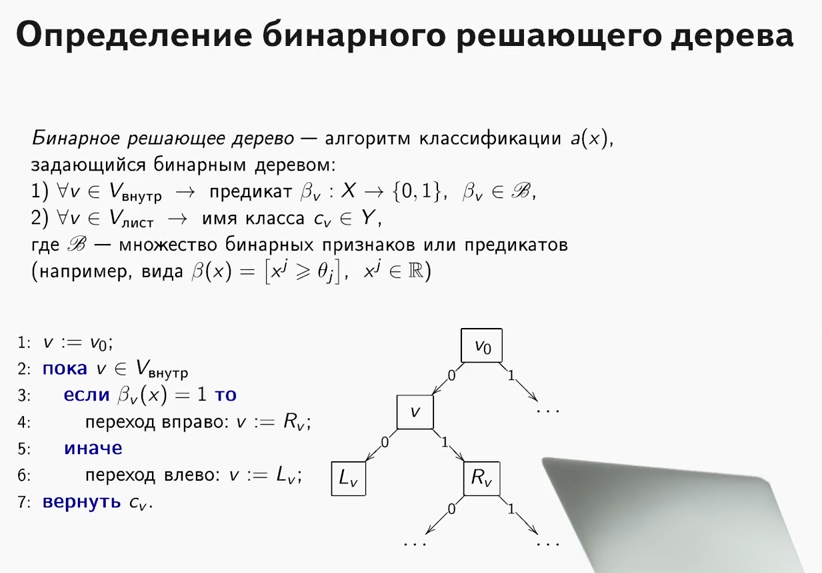
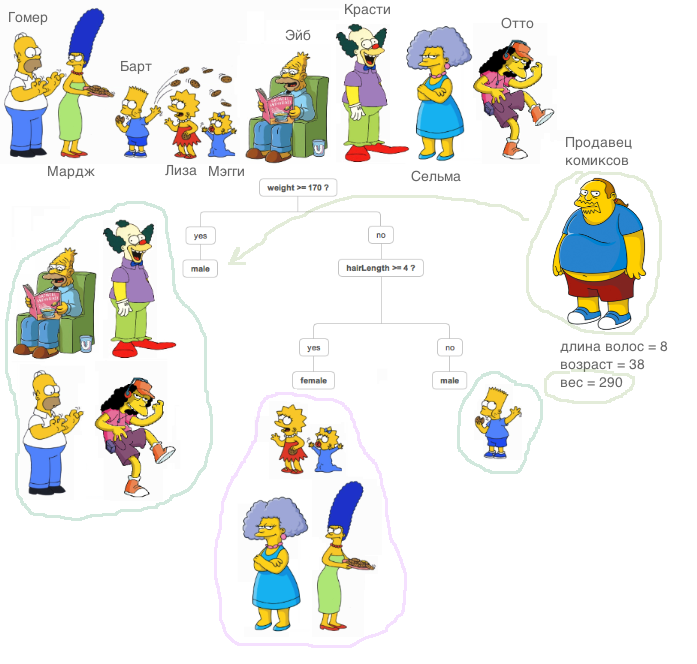
那么，您需要了解什么并且能够学习如何从头开始编写带有决策树的整体算法？ 由于算法的集合无非是“弱算法”的组合，因此编写好的集合需要好的“弱算法”，因此我们将在本文中对其进行详细分析。 顾名思义，这些都是至关重要的树，并且从简单到复杂，我们将学习如何编写它们。 在这种情况下，重点将直接放在实现上，整个理论将在最低限度内介绍，基本上我将提供独立研究材料的链接。

要学习这些材料，您需要了解我们的算法的优劣。 我们将非常简单地理解-我们将修复一些特定的数据集，并将我们的算法与Sklearn中的树算法进行比较（好吧，如果没有此库，将会发生什么）。 我们将进行很多比较：算法的复杂性，数据指标，正常运行时间等。

什么是果树？ ODS课程中包含很好的材料，它解释了决策树的原理（顺便说一句，很酷的课程，我向开始学习ML的人推荐它）。

一个非常重要的解释：在下面描述的所有情况下，所有符号都是真实的，我们不会对算法外部的数据进行特殊转换（我们比较算法而不是数据集）。

现在让我们学习如何使用决策树解决回归问题。 我们将使用MSE指标作为熵。

我们实现了一个非常简单的基于递归方法的RegressionTree类。 故意地，我们从一个效率很低但易于理解的类的实现开始，以便将来能够对其进行改进。

1. RegressionTree（）类

 class RegressionTree(): '''  RegressionTree   .    ,      . ''' def __init__(self, max_depth=3, n_epoch=10, min_size=8): '''   . ''' self.max_depth = max_depth #   self.min_size = min_size #    self.value = 0 #    (   ) self.feature_idx = -1 #    self.feature_threshold = 0 #    self.left = None #   self.right = None #   def fit(self, X, y): '''   .     . ''' #    self.value = y.mean() base_error = ((y - self.value) ** 2).sum() error = base_error flag = 0 #       prev_error_left = base_error prev_error_right = 0 #     0 -  if self.max_depth <= 1: return dim_shape = X.shape[1] #       left_value = 0 right_value = 0 #     for feat in range(dim_shape): #   idxs = np.argsort(X[:, feat]) #        N = X.shape[0] N1, N2 = N, 0 thres = 1 #      while thres < N - 1: N1 -= 1 N2 += 1 idx = idxs[thres] x = X[idx, feat] #    if thres < N - 1 and x == X[idxs[thres + 1], feat]: thres += 1 continue # ,         target_right = y[idxs][:thres] target_left = y[idxs][thres:] mean_right = y[idxs][:thres].mean(), mean_left = y[idxs][thres:].mean() #        - #   (  ) left_shape = target_left.shape[0] right_shape = target_right.shape[0] mean_left_array = [mean_left for _ in range(left_shape)] mean_right_array = [mean_right for _ in range(right_shape)] #      prev_error_left = N1/N * mse(target_left, mean_left_array) prev_error_right = N2/N * mse(target_right, mean_right_array) #    ,   if (prev_error_left + prev_error_right < error): if (min(N1,N2) > self.min_size): self.feature_idx = feat self.feature_threshold = x left_value = mean_left right_value = mean_right flag = 1 error = prev_error_left + prev_error_right thres += 1 #     ,  if self.feature_idx == -1: return #   -   ,    #   -     self.left = RegressionTree(self.max_depth - 1) self.left.value = left_value self.right = RegressionTree(self.max_depth - 1) self.right.value = right_value #   idxs_l = (X[:, self.feature_idx] > self.feature_threshold) idxs_r = (X[:, self.feature_idx] <= self.feature_threshold) #  self.left.fit(X[idxs_l, :], y[idxs_l]) self.right.fit(X[idxs_r, :], y[idxs_r]) def __predict(self, x): '''     -  ,         self.value -    . ''' if self.feature_idx == -1: return self.value if x[self.feature_idx] > self.feature_threshold: return self.left.__predict(x) else: return self.right.__predict(x) def predict(self, X): '''    -      __predict(). ''' y = np.zeros(X.shape[0]) for i in range(X.shape[0]): y[i] = self.__predict(X[i]) return y 

我将在这里简要说明每种方法的作用。

顾名思义， fit方法指导模型。 将训练样本应用于输入，并进行树训练过程。 排序这些符号，我们正在寻找减少熵的树的最佳分区，在本例中为mse 。 确定是否可以找到一个很好的拆分非常简单，足以满足两个条件。 我们不希望有任何物体掉入该分区（防止再训练），并且mse的平均误差应小于树中现在的误差-我们正在寻找相同的信息增益 。 以这种方式浏览所有标志和所有唯一值之后，我们将浏览所有选项并选择最佳分区。 然后，对接收到的分区进行递归调用，直到满足退出递归的条件为止。

顾名思义， __predict方法构成谓词。 接收到对象作为输入后，它会遍历结果树的节点-在每个节点中，属性号和值都固定在其上，然后根据对象的传入方法对该属性使用的值，我们去向右后代或向左去，直到我们到达工作表，在该工作表中将找到该对象的答案。

仅对一组对象， predict方法与以前的方法相同。

我们导入著名的加利福尼亚房屋数据集。 这是一个常规数据集，具有数据和解决回归问题的目标。

 data = datasets.fetch_california_housing() X = np.array(data.data) y = np.array(data.target) 

好吧，让我们开始比较！ 首先，让我们看看该算法的学习速度。 我们在Sklearn和我们自己中设置唯一的参数max_depth ，使其等于2。

 %%time A = RegressionTree(2) #    A.fit(X,y) 

 from sklearn.tree import DecisionTreeRegressor %%time model = DecisionTreeRegressor(max_depth=2) #  Sklearn model.fit(X,y) 

将显示以下内容：

• 对于我们的算法-CPU时间：用户4min 47s，sys：8.25 ms，总计：4min 47s
  挂墙时间：4分47秒
• 对于Sklearn-CPU时间：用户53.5 ms，sys：0 ns，总计：53.5 ms
  墙壁时间：53.4毫秒

如您所见，该算法学习速度慢了数千倍。 是什么原因 让我们做对。

回顾如何找到最佳分区的过程是如何安排的。 如您所知，通常情况下，对象的大小 $$$N$ 并带有标志的数量 $$$d$ ，找到最佳分割的困难是 $$$O（N * logN * d）$ 。

这种复杂性从何而来？

首先，为了有效地重新计算错误，有必要对所有列进行排序，以便在通过属性之前从最小列移到最大列。 当我们针对每个特征进行此操作时，会产生相应的复杂性。 如您所见，我们对符号进行了排序，但是麻烦在于重新计算错误-每次将数据驱动到适用于该行的mse方法中时。 这使得错误重新计数效率如此之低！ 毕竟，找到拆分的难度增加到 $$$O（N ^ 2 * d）$ 大 $$$N$ 极大地减慢了算法的速度。 因此，我们可以顺利进行下一个项目。

2.具有快速错误重新计数的RegressionTree（）类

需要采取什么措施来快速重新计算错误？ 拿一支笔和纸，画我们应该如何改变公式。

假设在某个步骤中已经针对 $$$N$ 对象。 它具有以下公式： $$$\ sum_ {i = 1} ^ n（y_i-\ frac {\ sum_ {i = 1} ^ N y_i} {N}）^ 2$ 。 在这里有必要除以 $$$N$ 但现在我们忽略它。 我们想迅速得到这个错误- $$$\ sum_ {i = 1} ^ {N-1}（y_i-\ frac {\ sum_ {i = 1} ^ {N-1} y_i} {N-1}）^ 2$ ，即抛出元素引入的错误 $$$y_i$ 到另一部分。

由于我们抛出了对象，因此必须在两个地方重新计算错误-右侧（不包括此对象）和左侧（考虑到此对象）。 但是在不失一般性的前提下，我们将仅推导一个公式，因为它们将是相似的。

由于我们使用了mse ，因此mse走运：要快速重新计算错误相当困难，但是当使用其他指标（例如，吉尼标准，如果我们要解决分类问题）时，快速重新计算要容易得多。

好吧，让我们开始推导公式！

$$

$$\ sum_ {i = 1} ^ N（y_i-\ frac {\ sum_ {i = 1} ^ N y_i} {N}）^ 2 = \ sum_ {i = 1} ^ {N-1}（y_i- \ frac {\ sum_ {i = 1} ^ N y_i} {N}）^ 2 +（y_N-\ frac {\ sum_ {i = 1} ^ N y_i} {N}）^ 2$$

我们将写第一个成员：

$$

$$\ sum_ {i = 1} ^ {N-1}（y_i-\ frac {\ sum_ {i = 1} ^ N y_i} {N}）^ 2 = \ sum_ {i = 1} ^ {N-1 }（y_i-\ frac {\ sum_ {i = 1} ^ {N-1} y_i + y_N} {N}）^ 2 = \\ \ sum_ {i = 1} ^ {N-1}（\ frac { Ny_i-\ sum_ {i = 1} ^ {N-1} y_i} {N}-\ frac {y_N} {N}）^ 2 = \\ \ sum_ {i = 1} ^ {N-1}（\ frac {（N-1）y_i-\ sum_ {i = 1} ^ {N-1} y_i} {N}-\ frac {y_N-y_i} {N}）^ 2 = \\ \ sum_ {i = 1 } ^ {N-1}（\ frac {（N-1）y_i-\ sum_ {i = 1} ^ {N-1} y_i} {N}）^ 2-2（\ frac {{N-1） y_i-\ sum_ {i = 1} ^ {N-1} y_i} {N}）\ frac {y_N-y_i} {N} +（\ frac {y_N-y_i} {N}）^ 2 = \\ \ sum_ {i = 1} ^ {N-1}（\ frac {（N-1）y_i-\ sum_ {i = 1} ^ {N-1} y_i} {N}）^ 2-\ sum_ {i = 1} ^ {N-1}（2（\ frac {（N-1）y_i-\ sum_ {i = 1} ^ {N-1} y_i} {N}）\ frac {y_N-y_i} {N} -（\ frac {y_N-y_i} {N}）^ 2）= \\ \ sum_ {i = 1} ^ {N-1}（\ frac {（N-1）y_i-\ sum_ {i = 1} ^ {N-1} y_i} {N-1}）^ 2 *（\ frac {N-1} {N}）^ 2-\ sum_ {i = 1} ^ {N-1}（2（\ frac {（N-1）y_i-\ sum_ {i = 1} ^ {N-1} y_i} {N}）\ frac {y_N-y_i} {N}-\\-（\ frac {y_N-y_i} { N}）^ 2）$$

gh，只剩一点点。 它仅表示所需数量。

$$

$$\ sum_ {i = 1} ^ {N}（y_i-\ frac {\ sum_ {i = 1} ^ {N} y_i} {N}）^ 2 = \ sum_ {i = 1} ^ {N-1 }（\ frac {（N-1）y_i-\ sum_ {i = 1} ^ {N-1} y_i} {N-1}）^ 2 *（\ frac {N-1} {N}）^ 2 -\\ \ sum_ {i = 1} ^ {N-1}（2（\ frac {（N-1）y_i-\ sum_ {i = 1} ^ {N-1} y_i} {N}）（\ frac {y_N-y_i} {N}）-（\ frac {y_N-y_i} {N}）^ 2）+（y_N-\ sum_ {i = 1} ^ {N} \ frac {y_i} {N}） ^ 2$$

然后很明显如何表达所需的金额。 要重新计算误差，我们只需要存储左右元素的总和以及到达输入的新元素本身。 现在重新计算该错误 $$$O（1）$ 。

好吧，让我们在代码中实现它。

 class RegressionTreeFastMse(): '''  RegressionTree    .        O(1). ''' #    def __init__(self, max_depth=3, min_size=10): self.max_depth = max_depth self.min_size = min_size self.value = 0 self.feature_idx = -1 self.feature_threshold = 0 self.left = None self.right = None #   -     def fit(self, X, y): #   -   y self.value = y.mean() #   - mse     (  # ,     )   base_error = ((y - self.value) ** 2).sum() error = base_error flag = 0 #     if self.max_depth <= 1: return dim_shape = X.shape[1] left_value, right_value = 0, 0 for feat in range(dim_shape): prev_error1, prev_error2 = base_error, 0 idxs = np.argsort(X[:, feat]) #      mean1, mean2 = y.mean(), 0 sm1, sm2 = y.sum(), 0 N = X.shape[0] N1, N2 = N, 0 thres = 1 while thres < N - 1: N1 -= 1 N2 += 1 idx = idxs[thres] x = X[idx, feat] #   -        delta1 = (sm1 - y[idx]) * 1.0 / N1 - mean1 delta2 = (sm2 + y[idx]) * 1.0 / N2 - mean2 #   sm1 -= y[idx] sm2 += y[idx] #    O(1) prev_error1 += (delta1**2) * N1 prev_error1 -= (y[idx] - mean1)**2 prev_error1 -= 2 * delta1 * (sm1 - mean1 * N1) mean1 = sm1/N1 prev_error2 += (delta2**2) * N2 prev_error2 += (y[idx] - mean2)**2 prev_error2 -= 2 * delta2 * (sm2 - mean2 * N2) mean2 = sm2/N2 #       if thres < N - 1 and np.abs(x - X[idxs[thres + 1], feat]) < 1e-5: thres += 1 continue # 2 ,    -   #   - -    if (prev_error1 + prev_error2 < error): if (min(N1,N2) > self.min_size): #         self.feature_idx, self.feature_threshold = feat, x #     left_value, right_value = mean1, mean2 #  -     flag = 1 error = prev_error1 + prev_error2 thres += 1 #   ,  if self.feature_idx == -1: return self.left = RegressionTreeFastMse(self.max_depth - 1) # print ("    %d"%(self.max_depth - 1)) self.left.value = left_value self.right = RegressionTreeFastMse(self.max_depth - 1) # print ("    %d"%(self.max_depth - 1)) self.right.value = right_value idxs_l = (X[:, self.feature_idx] > self.feature_threshold) idxs_r = (X[:, self.feature_idx] <= self.feature_threshold) self.left.fit(X[idxs_l, :], y[idxs_l]) self.right.fit(X[idxs_r, :], y[idxs_r]) def __predict(self, x): if self.feature_idx == -1: return self.value if x[self.feature_idx] > self.feature_threshold: return self.left.__predict(x) else: return self.right.__predict(x) def predict(self, X): y = np.zeros(X.shape[0]) for i in range(X.shape[0]): y[i] = self.__predict(X[i]) return y 

我们来衡量一下现在花在培训上的时间，并与Sklearn的类似产品进行比较。

 %%time A = RegressionTreeFastMse(4, min_size=5) A.fit(X,y) test_mytree = A.predict(X) test_mytree 

 %%time model = DecisionTreeRegressor(max_depth=4) model.fit(X,y) test_sklearn = model.predict(X) 

• 对于我们的算法，我们获得-CPU时间：用户3.11 s，sys：2.7 ms，总计：3.11 s
  挂墙时间：3.11 s。
• 对于Sklearn中的算法-CPU时间：用户45.9 ms，sys：1.09 ms，总计：47 ms
  挂墙时间：45.7毫秒。

结果已经更加令人愉快。 好吧，让我们进一步改进算法。

3.具有特征线性组合的RegressionTree（）类

现在，在我们的算法中，没有以任何方式使用属性之间的关系。 我们修复一个功能，仅查看空间的正交分区。 如何学习使用属性之间的线性关系？ 也就是说，寻找最佳的分区并不像 $$$a_ {feat} <x$ 和 $$$\ sum_ {i = 1} ^ K b_i * a_i <x$ 在哪里 $$$K$ -一些数字小于我们空间的大小吗？

有很多选择，从我的角度来看，我将重点介绍其中最有趣的两个。 这两种方法在弗里德曼的书中有所描述（他发明了这些树）。

我将提供一张图片，以便清楚地说明其含义：



首先，您可以尝试通过算法找到这些线性分区。 显然，不可能对所有线性组合进行分类，因为组合的数量是无限的，所以这种算法应该很贪心，也就是说，在每次迭代时，都要改善前一次迭代的结果。 该算法的主要思想可以在书中阅读，我还将在这里留下指向我的朋友和同事执行该算法的存储库的链接。

其次，如果我们不偏离寻找最佳正交分区的想法，那么我们如何修改数据集，以便使用有关要素关系的信息，并且搜索基于正交分区？ 是的，可以将原始功能转换为新功能。 例如，您可以将某些功能组合加起来，并已经按功能查找分区。 这种方法更不适合算法概念，但它执行其任务-它已经在某种属性互连中搜索正交分区。

好吧，让我们实现它-我们将添加新功能，例如，各种特征和的组合 $$$我，j$ 在哪里 $$$我<j$ 。 我注意到在这种情况下算法的复杂性将会增加，很明显会增加多少次。 好吧，为了更快一点，我们将使用cython。

 %load_ext Cython %%cython -a import itertools import numpy as np cimport numpy as np from itertools import * cdef class RegressionTreeCython: cdef public int max_depth cdef public int feature_idx cdef public int min_size cdef public int averages cdef public np.float64_t feature_threshold cdef public np.float64_t value cpdef RegressionTreeCython left cpdef RegressionTreeCython right def __init__(self, max_depth=3, min_size=4, averages=1): self.max_depth = max_depth self.min_size = min_size self.value = 0 self.averages = averages self.feature_idx = -1 self.feature_threshold = 0 self.left = None self.right = None def data_transform(self, np.ndarray[np.float64_t, ndim=2] X, list index_tuples): #   -       for i in index_tuples: #  ,       X = np.hstack((X, X[:, i[0]:(i[1]+1)].sum(axis=1).reshape(X.shape[0],1))) return X def fit(self, np.ndarray[np.float64_t, ndim=2] X, np.ndarray[np.float64_t, ndim=1] y): cpdef np.float64_t mean1 = 0.0 cpdef np.float64_t mean2 = 0.0 cpdef long N = X.shape[0] cpdef long N1 = X.shape[0] cpdef long N2 = 0 cpdef np.float64_t delta1 = 0.0 cpdef np.float64_t delta2 = 0.0 cpdef np.float64_t sm1 = 0.0 cpdef np.float64_t sm2 = 0.0 cpdef list index_tuples cpdef list stuff cpdef long idx = 0 cpdef np.float64_t prev_error1 = 0.0 cpdef np.float64_t prev_error2 = 0.0 cpdef long thres = 0 cpdef np.float64_t error = 0.0 cpdef np.ndarray[long, ndim=1] idxs cpdef np.float64_t x = 0.0 #        #  ,     if self.averages: stuff = list(range(0,X.shape[1],1)) index_tuples = list(combinations(stuff,2)) #    X = self.data_transform(X, index_tuples) #   -   y self.value = y.mean() #   - mse     (  , #     )   base_error = ((y - self.value) ** 2).sum() error = base_error flag = 0 #     if self.max_depth <= 1: return dim_shape = X.shape[1] left_value, right_value = 0, 0 for feat in range(dim_shape): prev_error1, prev_error2 = base_error, 0 idxs = np.argsort(X[:, feat]) #      mean1, mean2 = y.mean(), 0 sm1, sm2 = y.sum(), 0 N = X.shape[0] N1, N2 = N, 0 thres = 1 while thres < N - 1: N1 -= 1 N2 += 1 idx = idxs[thres] x = X[idx, feat] #   -        delta1 = (sm1 - y[idx]) * 1.0 / N1 - mean1 delta2 = (sm2 + y[idx]) * 1.0 / N2 - mean2 #   sm1 -= y[idx] sm2 += y[idx] #    O(1) prev_error1 += (delta1**2) * N1 prev_error1 -= (y[idx] - mean1)**2 prev_error1 -= 2 * delta1 * (sm1 - mean1 * N1) mean1 = sm1/N1 prev_error2 += (delta2**2) * N2 prev_error2 += (y[idx] - mean2)**2 prev_error2 -= 2 * delta2 * (sm2 - mean2 * N2) mean2 = sm2/N2 #       if thres < N - 1 and np.abs(x - X[idxs[thres + 1], feat]) < 1e-5: thres += 1 continue # 2    -   #   -      if (prev_error1 + prev_error2 < error): if (min(N1,N2) > self.min_size): #         self.feature_idx, self.feature_threshold = feat, x #     left_value, right_value = mean1, mean2 #  -     flag = 1 error = prev_error1 + prev_error2 thres += 1 # self.feature_idx -     . #   -  ,    -   #  ,   ,     #   ,  if self.feature_idx == -1: return #    self.left = RegressionTreeCython(self.max_depth - 1, averages=0) self.left.value = left_value self.right = RegressionTreeCython(self.max_depth - 1, averages=0) self.right.value = right_value #      idxs_l = (X[:, self.feature_idx] > self.feature_threshold) idxs_r = (X[:, self.feature_idx] <= self.feature_threshold) #   self.left.fit(X[idxs_l, :], y[idxs_l]) self.right.fit(X[idxs_r, :], y[idxs_r]) def __predict(self, np.ndarray[np.float64_t, ndim=1] x): if self.feature_idx == -1: return self.value if x[self.feature_idx] > self.feature_threshold: return self.left.__predict(x) else: return self.right.__predict(x) def predict(self, np.ndarray[np.float64_t, ndim=2] X): #   ,        if self.averages: stuff = list(range(0,X.shape[1],1)) index_tuples = list(itertools.combinations(stuff,2)) X = self.data_transform(X, index_tuples) y = np.zeros(X.shape[0]) for i in range(X.shape[0]): y[i] = self.__predict(X[i]) return y 

4.结果比较

好吧，让我们比较一下结果。 我们将比较三种具有相同参数的算法-Sklearn的树，我们的普通树和具有新功能的树。 我们将多次将数据集分为训练集和测试集，然后计算误差。

 from sklearn.model_selection import KFold def get_metrics(X,y,n_folds=2, model=None): kf = KFold(n_splits=n_folds, shuffle=True) kf.get_n_splits(X) er_list = [] for train_index, test_index in kf.split(X): X_train, X_test = X[train_index], X[test_index] y_train, y_test = y[train_index], y[test_index] model.fit(X_train,y_train) predict = model.predict(X_test) er_list.append(mse(y_test, predict)) return er_list 

现在让我们运行所有算法。

 import matplotlib.pyplot as plt data = datasets.fetch_california_housing() X = np.array(data.data) y = np.array(data.target) er_sklearn_tree = get_metrics(X,y,30,DecisionTreeRegressor(max_depth=4, min_samples_leaf=10)) er_fast_mse_tree = get_metrics(X,y,30,RegressionTreeFastMse(4, min_size=10)) er_averages_tree = get_metrics(X,y,30,RegressionTreeCython(4, min_size=10)) %matplotlib inline data = [er_sklearn_tree, er_fast_mse_tree, er_averages_tree] fig7, ax7 = plt.subplots() ax7.set_title('') ax7.boxplot(data, labels=['Sklearn Tree', 'Fast Mse Tree', 'Averages Tree']) plt.grid() plt.show() 

结果：



我们的常规树输给了Sklearn（这是可以理解的：Sklearn经过了很好的优化，默认情况下，它在树中使用了许多我们没有考虑的参数），但是当添加数量时，结果会变得更加令人愉悦。

总结：我们学习了如何从头开始编写决定性的树，学习了如何提高其性能，并通过将其与Sklearn的算法进行比较，在实际数据集上测试了它们的有效性。 但是，此处介绍的方法并不限制算法的改进，因此请记住，所提出的代码可以做得更好。 在下一篇文章中，我们将基于这些算法编写Boosting。

一切成功！