在不使用伯努利方程的情况下解释“提升力”现象的物理性质

Monin Ilya Alekseevich，MSTU技术科学候选人，以鲍曼（Bauman。），SM-9和imoninpgd@gmail.com的名字命名

对飞机机翼升力的现有理论解释的批评

在听完莫斯科物理技术学院航空力学与飞机工程学院（FALT）的“空气动力学入门”课程并阅读了几篇关于“空气动力学”的大学生后，我对空气（气体或理想气体）周围流的物理解释中的许多明显矛盾感到困惑。液体），并在机翼上形成升力。

1. 由“版本”传播的机翼上升力形成的主要形式是机翼上方和机翼下方的空气（液体）流动速度的差异，因此根据伯努利定律会出现压力下降。 在这种情况下，通过伯努利定律，机翼表面的计算流速与机翼上记录的机翼压力明确相关，而忽略了基于物理学基本定律的其他可能解释。
2. 在分析理想的无粘性液体在平面流中的轮廓周围的流时，与基本速度V0相比，流量获得了惊人的大幅增加。 就是说，能量守恒定律被反驳，因为从任何地方获取能量以加速流动，超过了入射在机翼上的流动能量。 同时，忽略了流体力学的假设，根据伯努利定律，当射流从水平面以下冲出时，速度头受到船内静压力的唯一限制，即在机翼上加速后射流的速度头不能超过介质制动时压缩的静压力。

对于现代飞机的飞行，必要的提升力为500-600kg / m.sq。 起飞和降落时，现代飞机的速度约为250 km / h。 在这种情况下，以大约450 km / h的上平面的流速在机翼上提供必要的提升力。

这种气流没有可见的加速机制的机制是什么？

实际上，机翼与即将来临的气流的接触只会导致气流的减速，而不会导致其加速！

这些矛盾必须消除！

为了美丽而复杂的数学构造，物理学一定不能失去其物理意义！

让我们考虑另一种关于机翼升力形成的解释，而没有发现违反物理定律和常识的情况。 这将需要应用普通力学定律。

考虑到这一点，我们认为空气是由具有各自质量的单个粒子（相互排斥（产生气体压力））组成的，当改变其方向和速度时，每个粒子都遵循力学定律。

机翼上稀疏度与流量增加之间的关系不明确

所考虑的实际机翼不是伯努利定律模型中理想管的元素，而是在移动的真实气体的无限空间中的有限固体物体，该气体由质量和尺寸相当明显的气体颗粒组成。 在这种情况下，应该考虑到垂直于速度矢量和机翼表面的惯性力和所产生的压力，考虑到机翼弯曲表面上的射流的弯曲流动。

如果我们考虑射流在机翼轮廓上的运动，那么由于气流的曲率，气流会在机翼上产生真空。

因此，要弯曲物体的直线运动，需要在垂直于速度矢量的方向上施加力。 在连续的平面流的情况下，就其曲率而言，必须确保其上方和下方的压力差。 同时，射流凸面的压力会增加，而凹面的压力会降低。
当绕实体点的圆周移动时，将通过力产生向心加速度

F = m * V ^ 2 / R

并且在厚度为dR的薄气体层的相同圆周运动下，质量等于

m = q * S * dR ，

其中S是气体层的面积，q是气体的密度。 如果将向心力带到气体层的基本区域，则该力将变为压力

P = q * V ^ 2 * dR / R

当气流在机翼表面上方流动时，气体层沿弯曲路径移动。 该轨迹的每个点都有自己的曲率半径，这使我们能够在垂直于速度的方向上计算惯性气体压力。

因此，可以从在其表面上方流动的气体层直接计算机翼上的压力（真空），并且始终将气流速度假定为等于机翼速度Vo。

首先，我们考虑机翼最简单的情况，即以半径R弯曲的零厚度板形式的机翼。 这种薄的弯曲轮廓用于飞机模型中的超轻滑翔机。

顺便说一下，根据通常的伯努利定律理论，薄的弯曲板根本不应该具有任何升力，因为机翼下方和机翼上方的路径长度是相同的。 但是细翼具有升力，而且非常重要，这清楚地表明了使用伯努利定律的升力模型的不正确性。

为了估算机翼，我们将选择低速飞机通常的轮廓高度，即机翼宽度的20％。 在这种情况下，对于轮廓的高度，我们采用相对于水平气流的前缘和后缘的高度之差（见图1-3）。


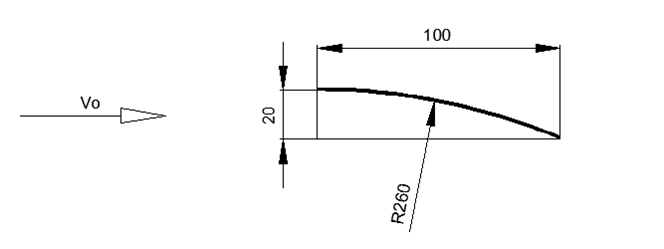图1。 恒定曲率的细翼几何


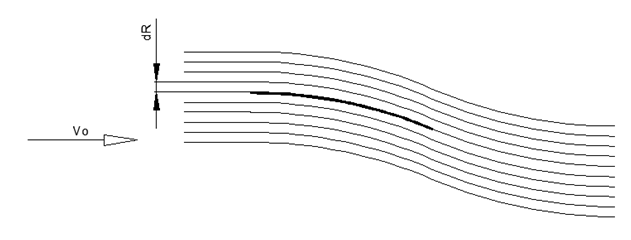图2。 细半径机翼周围的估计流量


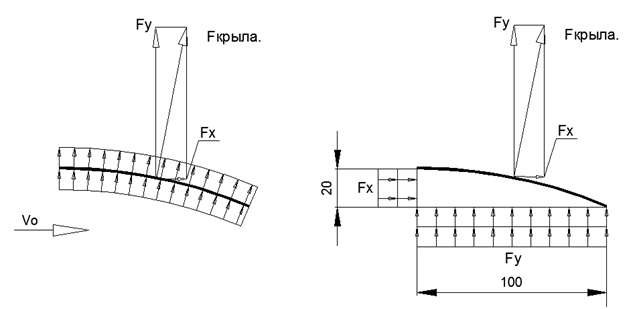图3。 细半径机翼上压力分布的性质以及方向上的合力

然后，如果宽度为1 m，高度为轮廓的20％，则机翼半径为2.6 m，前提是机翼的切线在轮廓的顶部为水平。

现在，我们从沿弧形弯曲的空气层计算出机翼的向心压力。

因此，对于70 m / s（252 km / h）的速度，一层厚度为0.1 m，曲率半径为2.6 m的层的压力为235.6 Pa或24 kg / m.sq。，而在70 m / s的速度头的值为3063 Pa。

假设薄机翼从两侧流过，那么这些值必须至少翻倍，然后再乘以一定数量的平行层，这些平行层也被移动机翼弯曲。 如果我们假设扰动层的厚度不小于机翼两侧的机翼宽度的一半，那么我们获得的机翼总十倍载荷约为2356 Pa。 这些数字超过了机翼厚且机翼表面曲率相似的低速轻型飞机的机翼载荷值。 （见表1）

由于压力Pcr被施加到薄板的弯曲表面，因此来自Pcr的力Fcr可以被分解为提升力Fy和抗飞行阻力Fx。
提升力Fy等于机翼整个区域上来自曲线流Pcr压力的力在Y轴上的投影的积分。

在圆形机翼受到均匀压力的情况下，Fy的值将等于机翼在X轴上的投影面积乘以Pcr的乘积Pcr，该乘积等于机翼的S = B * L（在这种情况下为1m.sq./m.p。）。

Fy = Pkr * Bkr = 2356 * 1 = 2356 N / m.p.

同时，在这种情况下，水平运动的阻力将等于整个机翼区域在X轴上的投影积分dFcr。 在机翼受到均匀压力的情况下，Fx的值将等于机翼在Y轴上的投影面积乘以乘积Pcr，该乘积等于机翼轮廓的高度H（在这种情况下为0.2平方米/米）。

Fx = Pkr * Nkr = 2356 * 0.2 = 462 N / m.p。

在这种情况下，我们获得K = Fy / Fx =（Pkr * Vkr）/（Pkr * Nkr）= Bkr / Nkr，即在圆形薄轮廓上施加均匀压力的情况下，机翼质量仅等于轮廓K = B / N的几何参数之比。

根据给定图片的力矢量膨胀规则，您可以立即获得机翼质量的值K = Fy / Fx，在这种情况下等于K = 100 * Pkr / 20 * Pkr = 5。

有趣的是，如果将计算出的机翼的缩放比例缩小十倍（沿曲率半径，轮廓的高度和宽度），则机翼上的压力在相等的飞行速度下将保持不变（请参见表2）。 出于这个原因，重型巡航导弹会在较小而薄的机翼上飞行。 事实证明，它们的小而薄的机翼具有足够的曲率，足以产生必要的提升力！

由于房间建模足够便宜，因此可以在完整比例的模型上简单地检查这些数字。

表1。 恒定半径R = 2.6 m的机翼上弯曲空气层的压力取决于飞行速度。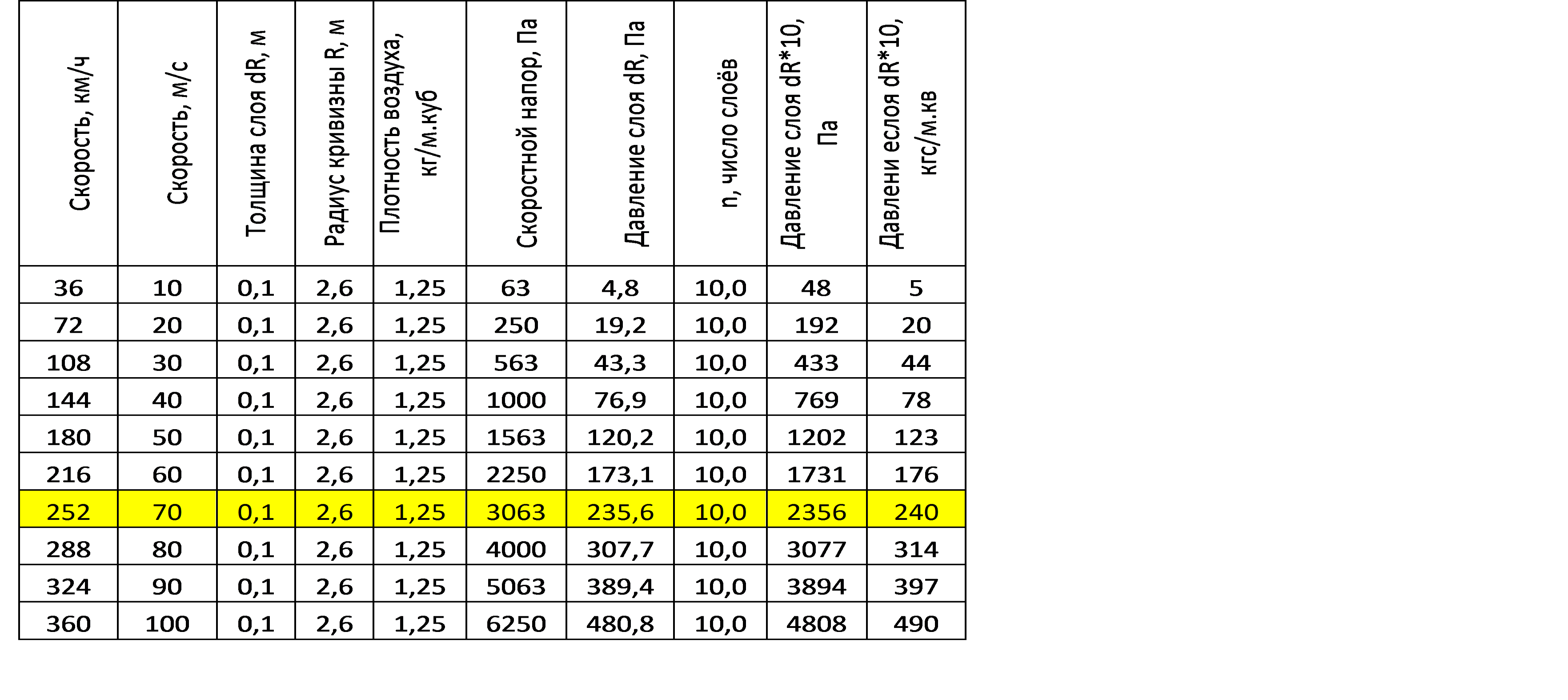



表2。 恒定半径R = 0.26 m的机翼上的弯曲空气层的压力取决于飞行速度。



有趣的是，考虑机翼Kkr如何以其恒定曲率Rkr改变，但轮廓宽度参数Vkr改变。 （见表3）

在表格的第一行，机翼的空气动力学质量达到了K = 182的惊人值，但机翼上的负载仅为67 Pa（7 kgf / m2），仅适用于机载大尺寸滑翔机模型。

机翼上必要的提升力仅在足够小的K型机翼上产生，这可以从表格的最后几行看到。

黄色栏显示变量参数和原始轮廓线（Kkr = 5）。

表3。 在恒定的飞行速度下，以不同的轮廓角（轮廓宽度）更改恒定半径R = 2.6 m的机翼参数。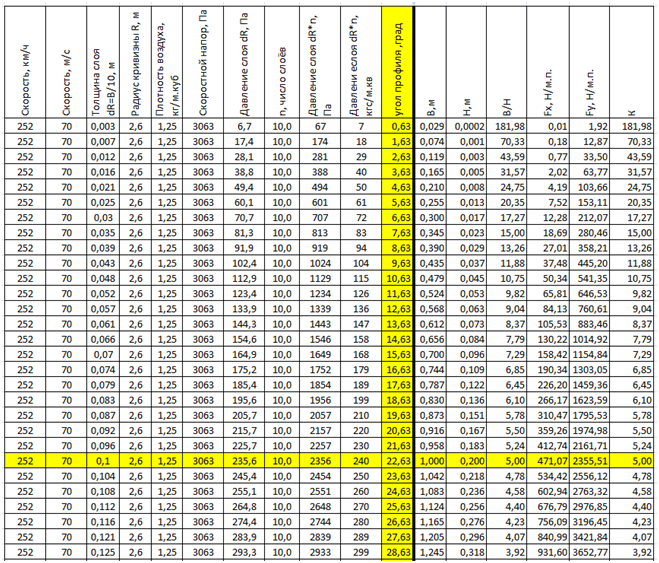



对于弦长不变的机翼，但对于恒定速度的曲率也不同的机翼，您还可以计算升力Fy的变化和机翼Kkr的质量。 以黄色突出显示的列是：可变参数Rcr-曲率半径和恒定轮廓宽度Vcr。 Kkr = 5的初始轮廓线也突出显示。

Tab.4。 以恒定的飞行速度以恒定的轮廓宽度B = 1 m更改曲率半径可变的机翼的参数。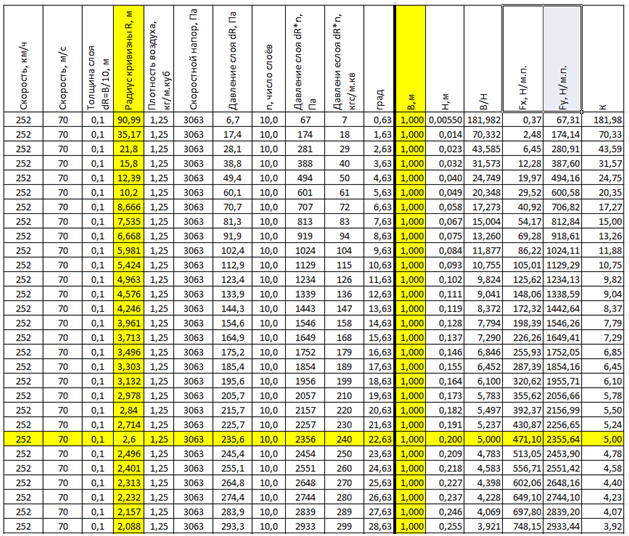



在所描述的模型中，为了在机翼上方获得真空，不需要在机翼上方额外加速空气。 在整个周围空间的静态空气压力的影响下，在机翼周围的气流明显弯曲的条件下，可以确保机翼上方有明显的排放。 初始弯曲板的弦的倾斜角为11.3度（弧段的一半为22.6度），这与现代客机机翼在机翼机械化释放（板条+襟翼）释放时的着陆方式非常吻合。 在着陆模式下，与传统的机翼较低的平直机翼相比，采用机械化释放的机翼使人联想到弯曲薄板的情况（见图4）。



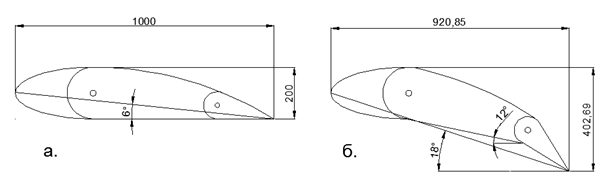图4。 不对称的机翼，其下部具有流线型的平坦表面：a）用于高速飞行的伸直位置； b）具有最大曲率的机翼，并完全释放了机械化力。

强弯曲的薄机翼被广泛用作风扇叶片。 低压值下的低线速度允许在风扇中使用厚度极小的薄钢板或塑料板作为风扇，因为它们的强度足以承受现有的负荷。

在重型飞机中，由于强度不足，在技术上不可能使用薄机翼。 机翼的大厚度使您可以在机翼内部放置相当高的承重梁，其强度和刚度足以弯曲和扭转，同时保持飞机可接受的重量。 出于这个原因，所有空气动力学研究机翼的厚度都相当明显。 因此，我们从考虑薄的弯曲板的空气动力学转变为具有实际厚度和不同曲率平面的机翼轮廓。

在考虑细翼机翼流动模型的最后，有必要对所提出的“机翼提升力”解释模型进行进一步的证明。 从力学上可以知道，强度是每单位时间动量的变化，即

F = d（米* V）/ dT

在围绕薄弯机翼的流动的浊音模型中，我们可以将升力Fy计算为传入气流的动量的垂直变化，这被认为是

Fy2 =（dR * 10 * q * Vo）* Vo * sinAcr ，

其中Vo是机翼速度，dR是计算模型中气流的基本弯曲层的厚度，10是要同时弯曲的层数，Acr是从机翼流向初始速度Vo的方向下降的角度。

完成计算后，我们得到两个计算得出相同的结果。

或以分析形式：

Fy1 = Pcr * Bcr ，

Pkr =（dR * 10 * q * Vo）* Vo / R ，

Bcr = R * sinAcr

将表达式Pkr和Bkr替换为Fy1的表达式，并在分子和分母中减去相同的名称R，我们得到：

Fy = Pkr * Bkr =（dR * 10 * q * Vo）* Vo * sinAcr

因此，等式Fy = Fy1 = Fy2始终为真

即，计算机翼的“提升力”的“惯性曲线”方法给出的公式与相同几何形状的机翼的“反作用力”方法相同。
这意味着飞机飞行不是由于来自“魔术涡流”的某种“魔术”力，而是由于向空中抛下空气时可理解的古老的“力的冲量”或“喷气推力”。

胖翼

在起飞和降落过程中的低速飞行下（M = 0.2或250 km / h），压头不超过3 kPa（海平面100 kPa时大气压的3％），也就是说，相对于基本大气压而言很小当在机翼附近拉动射流时，流动的几何压缩在视觉上变得无法察觉。

为了在机翼上方产生升力，必须产生气流的弯曲度，以使机翼处于气流的凹入区域。 确保机翼上方的射流的这种曲率有助于机翼上平面的曲率，该上平面位于机翼前导流板的空气动力学阴影中。

在这种情况下，机翼的下平面要么在不产生真空的情况下沿直线流动，要么在凹形表面上流动，从而将气流向下排出，从而从下方在机翼上产生正压力增加，并与来自机翼上方真空的提升力相结合。
在我们的案例中，厚机翼和薄板之间的主要区别在于前部整流罩的外观，在迎面而来的气流到达产生升力的弯曲平面之前将其散开。

在厚翼飞行的机翼前方出现制动区域，在该区域中，空气速度等于零（相对于机翼），并且该区域中的超压等于压头Pvo。

在不考虑空气压缩的情况下将不可能绘制流线，否则人们要么必须接受机翼表面上方空气加速的形式，要么具有流动曲线的影响区域将在不可压缩的介质中冲向无穷大，这是不可行的。
顺便说一下，实际上，这两种效应（流动加速和不可压缩液体中的无限影响区域）在具有当前烟流的风洞中以及潜艇在浅水深度移动时都得到了体现。

因此，在风洞（ADT）中，测试模型周围的流动发生时，在ADT模型壁的间隙中出现了明显的流动加速（烟雾线的厚度减小）。 那仅仅是对这种现象的解释，完全不正确地归因于形成力的流动的加速。 实际上，间隙“ ADT模型壁”中的气流加速仅是ADT流路中孔口变窄的结果，同时由于具有坚硬风扇特性的强大风扇而在ADT自身中保持了恒定的空气流量。

当潜艇在潜艇上方的较浅深度移动时，会形成视觉上明显的积水现象。 驼峰的值等于潜水艇船体前面的水量，当以给定速度移动时，必须以某种方式将其从潜水艇船体前面的区域移动到船尾区域。 当潜艇向深处移动时，也会在表面形成隆起，但是由于隆起的扩展区域较大，因此如果用简单的目视观察就无法检测到其隆起。 表面无法形成水的原因是由于无法将不可压缩的流体向底部移动，大气压下的薄水层很容易向表面移动，具有大气压和重力弹簧的明显弹性特征。 顺便说一下，即使潜艇在很深的深度移动，也可以通过使用高度灵敏的设备从卫星进行观测来检测出海浪（以及潜艇本身），该设备可以高精度地测量海洋的表面几何形状，并将海底的驼峰与海面的海浪噪声隔离开来。使用计算机。

因此，我们认为气体是可压缩的，并且我们将机翼护罩的影响区域设置为取决于射流在压力Pvo上的压缩比。

整流罩制动区域中的压力由包围整流罩的弯曲空气保持。 压力与空气层曲率的关系与薄的弯曲机翼dP = q * Vo ^ 2 * dR / Rsl的情况相同。

影响区域的大小（流动曲率明显）也与Vkr和Nkr的值相关。 , , () .

, /2=R.

, vo , /2= R.
Pr= vo.



qVo^2*R/R= qVo^2/2



R= 2* R

, , ( ), .

, . , . (..5).



.5. Vo .

Pvo , , , .

, . . (..6).

« » : « … , , ( ), …». .

, . - ( ) , , .

- ./. , «» (. .6).

, .



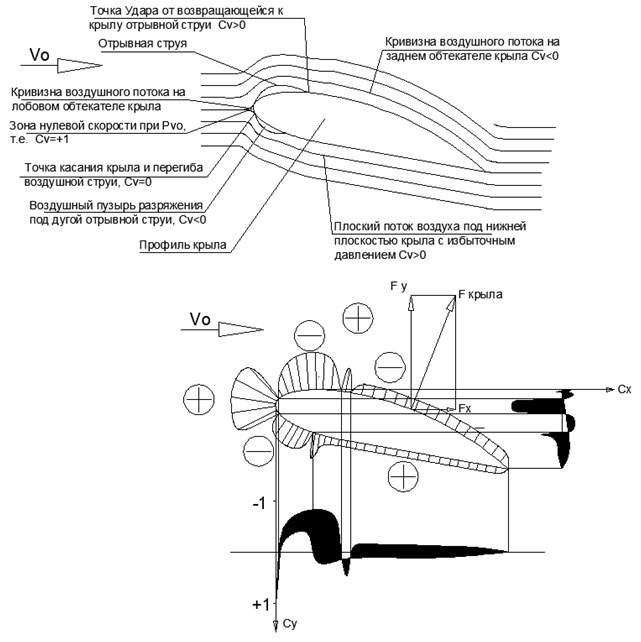.6. . . Y .

. . =1 , , , , . , ( ).
, . , Fy .

, «», , .

«» (..7). 4-5 (..1-2). «» , . , . .



.7. /=0,1 (10%) «» : ) ; ) .



.1. - 35 ( ).



.2. -29 - ( ).



.3. -29 .

(..3) «» : . , , . , . , , , , . -35 -57 , .

在网络中，您可以找到许多有关任何问题的说明性材料，包括飞机机翼上的涡流形成，例如：



同时，很容易在同一互联网上的云层中从飞机上找到涡旋痕迹的照片，这些照片证明了这种现象的规模比理论上试图显示的要大得多。



图片4。 在雾层的漩涡足迹在高空飞行的飞机后。 可见的雾状旋风的环距离飞机几百米，并且视觉距离是远摄镜头在几公里外拍摄飞机时产生的光学错觉。



图片5。 在雾层的漩涡足迹在高空飞行的飞机后。 可见的是垂直气流和从侧面进入的空气波，扭曲成与垂直向下气流接触的螺旋形。



图片6。 涡流在降落跑道上方跑道上方的雾层中拖曳。

由于机翼上的末端涡旋，这些在飞机后面的巨大纠缠旋风根本没有形成。 涡旋固然存在，但是它们的作用并不是很大，飞机设计师正在积极而成功地为之奋斗。

来自照片的大型涡流形成在飞机后面很远的地方，当飞机向下拉下的气流从两侧从下降层下方进入稀有空间的气流取代后，气流在两侧被取代（见图4-5）。 关于卫星涡旋形成的解释与已经考虑的“机翼对周围空间的影响范围”的问题相呼应。 在这种情况下，地表的作用在于由机翼向下投射的向下气流的分布边界。 也就是说，在没有坚实的下方表面的情况下，也可以进行飞机的飞行并创建``机翼的升力''，但与此同时，被抛落的气流将无限长地向下运动，随着气流的流失，其流失的速度和动能将消失，但保持垂直动量不变。 最初丢弃的空气质量的动能将因横向气流参与运动而损失，其对称多向性不会改变飞机机翼产生的初始总动量。 Photo.6清楚地说明了地球限制者的作用。 在那儿，着陆空中客车上方的直线雾流（见图6）直线下降到地面，然后，在飞机后面很远的地方，沿着地面限制器开始向两侧移动，并且从侧面和上方的雾层已经在卫星层的中间接近了，旋转向下流动的双自补偿螺旋。

在地球附近飞行机翼时的“屏幕效果”

鉴于地球在“机翼提升力”形成中所扮演的角色，因此有必要额外考虑“屏幕效应”，如果没有坚实的地球表面，则无法发生“屏幕效应”。 因此，机翼在无尽空域中飞行以及在地球附近的“屏幕效应”上的物理学具有截然不同的性质。

在低马赫数下基于气体可压缩性的Ekranoplan效应的解释

地球紧密间隔的表面对机翼升力的影响称为“屏蔽效应”。 有了这种效果，当机翼在坚实表面（地球，水）附近飞行时，机翼的升力会急剧增加，高度与机翼弦的大小相当。 基于这种效果，甚至是一整类低空飞行的车辆-WIG。

现象的本质是什么？ 仅通过假定空气为可压缩气体可以解决此问题。

然后，当机翼在地面上飞行时，在两个固体表面之间会形成有限尺寸的气隙。 当机翼以较小的正迎角飞行时，机翼下方的迎面气流从机翼的前缘到后缘逐渐受到压缩（见图8）。

机翼下方流动筛上的最大压缩压力仅取决于相对于飞行机翼的速度头，并且压缩层中的该压力不能超过空气速度头的压力：

Po = Vo ^ 2 * Q / 2 ，

其中，是机翼速度V®时的P速度空气压力，V®是机翼飞行速度，Q是空气密度。

知道机翼下的最大压力增量，我们就可以计算“气垫”间隙中的几何参数。

因此，在40 m / s（144 km / h）的速度下，速度头Po = 1 kPa或1 atm的1％。 （100kPa）。
也就是说，以40 m / s的速度，机翼下方的最大压力是通过压缩从机翼前缘到后部的间隙高度X的1％来实现的。 在眼睛上，这种预紧力几乎是无法检测到的，并且机翼下方的层在视觉上看起来是平坦的（见图8.a）。

迎角为A =（Po / Ratm）* X / V弧度（小角度sinA = A），
其中B是机翼弦，X是机翼后缘水平到机翼下方地面的空气间隙，R是机翼速度V®的风速头，Ratm是大气压力（海平面Ratm = 100 kPa）。

事实证明，获得屏幕效果的最大有效迎角取决于机翼在表面上方的高度，机翼的结构宽度和给定的飞行速度，迎角只是这些值的衍生。

结论：可以几乎无限地增加机翼宽度，将迎角减小到几乎为零，从而利用电阻的实际电感分量实现Cx的最小电阻。

低速飞行时的“屏蔽效果”可提供非常高的机翼质量，因为它在机翼上形成的最大比升力等于压头Ro的最大升力，而几乎完全平坦且非常薄的机翼迎角很小。 在屏幕上飞行期间，低马赫数的机翼质量可以达到K = 25-30。
与机翼下方的压力相比，在带有平坦机翼的“屏幕”上进行这种飞行时，机翼上凸面上的稀薄度贡献很小。

随着飞行速度的增加，速度头呈二次方增加，并且为了获得最大的屏蔽效果，有必要与速度头Po的增加成比例地提升迎角。

即，为了增加P 0而增加速度V 0导致迎角的增加速度的平方增加，这又急剧地降低了机翼的质量。 并且从一定的速度V-max开始，将具有大迎角的屏幕效果的大小与具有扩展机翼机械化的传统飞机在着陆模式下的提升力进行了比较。

对于任何具有弦B的机翼，要增加飞行高度X，必须提升迎角，之后WIG将升至新的高度X2，在此将在新的高度再次建立由于新的迎角导致的喷气机压缩程度的平衡。 同时，随着高度的增加，ekranoplan的飞行开始线性增加飞行阻力，并且相应的所需推力也在不改变飞行速度的情况下增加。 也就是说，ekranoplan飞行的燃油效率可以从仅几米的高度增加而急剧变化。 例如，金莺的最大飞行距离在0.8 m的高度下为1150公里，而在0.3米的相同载荷下的最大飞行距离已为1480公里。



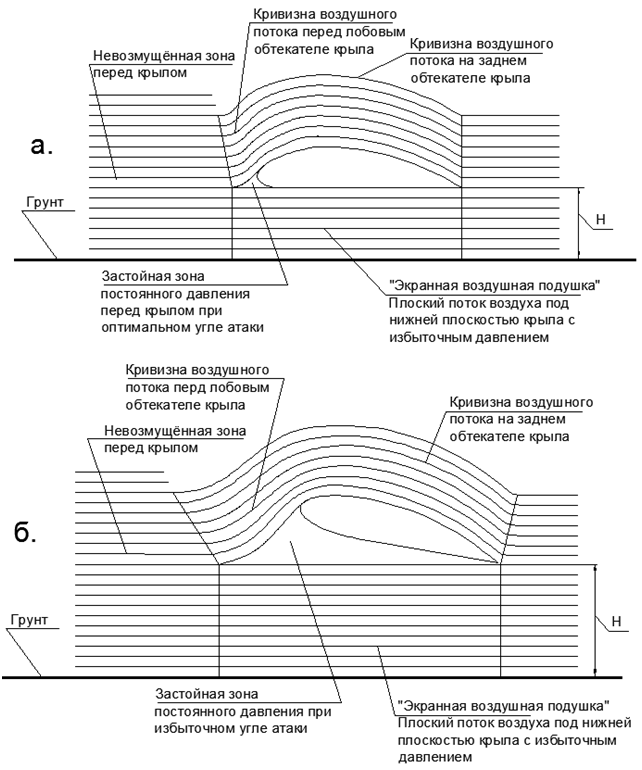图8。 “滤网效果”上的气流配置：a。）最佳迎角，机翼下方没有停滞区，b。）过大迎角在机翼和“滤网气垫”的压缩空气层之间形成了高压滞留大气泡。

结论：机翼迎角的额外撕裂而不增加屏幕上的飞行速度不会增加升力，而只会增加飞行阻力Cx（见图8.b）。

考虑到着陆器在降落模式下的翼弦角度约为15度，我们可以考虑翼弦B的值等于机翼X的高度来估计机翼下射流对压力Po和相应速度V0的压缩量。

15度对应于sin15 = 0.262

在15度的迎角下，应该有一个速度头Po = 0.26 atm = 26 kPa，但是这种压力是在非常高的速度（740 km / h）下实现的，并且远远超过了飞行所需的机翼负荷。 即，在250-300 km / h的着陆速度下，在跑道上产生遮蔽效果的如此大的着陆迎角是过大的。

机翼在15度迎角处的质量将下降至K = 3.7的总值。
客机的着陆速度仅为约250 km / h（70 m / s），而压头为Po = 3 kPa或仅为Ratm的3％，而正常飞行中的机翼负荷为5 kPa（500 kg / m.kv = 5％拉特）。 即，在着陆时，飞行员可以在与起落架的高度相当的高度上，与机翼B的宽度相当的高度上开始明显感受到客机的屏幕效果。 对准飞机并以250 km / h的速度减小迎角，使飞机能够穿透“屏幕气垫”，因为其承载能力低于机翼下方飞行所需的压力。
由于“屏幕效应”，飞机在水平飞行中会出现“无损”，而在压头Po = 5kPa（对应于Vo = 324 km / h或90m / s）下，机翼机械化不会以5％的攻角（或3度）释放机翼。

攻角5％（或3度）可产​​生等于K = 20的机翼质量。
高K = 30对应于3％（2度）的迎角，而机翼下的背压仅为3％* Ratm = 3 kPa（300 kg / m.sq.），对应于V®= 70 m / s（250 km / h）。

因此，与通常的高空“飞机”相比，“ ekranoplan”模式下具有成本效益的飞行模式位于低速区域。 当机翼的机翼质量低于K = 20时，使用普通的高空飞机进行运输更有利可图。 也就是说，WIG的经济有效运行区域对应于低于300 km / h的速度。

假发操纵

另一个需要考虑的是在飞行中操纵WIG的问题。 由于机翼在“屏幕”上的升力与高空飞行时形成的力不同，因此它甚至无法“通过飞机”操纵。

Ekranoplane无法在机翼上滚动而弯曲，因为它会立即在升起的机翼上失去升力，并且在机翼降下时会碰到水。 对于ekranoplan，旋转只能通过“煎饼”进行，即没有滚动，但只能通过从垂直尾部产生横向力来进行。

WIG本身的垂直尾巴也应与飞机尾巴不同。 WIG的垂直尾部应至少包括两个龙骨，这些龙骨应能够同时进行和随机工作，具体取决于执行的操纵类型。 在这种情况下，垂直羽状物不仅会绕其垂直轴进行WIG旋转，而且还会在飞行速度方向上产生水平力。
后龙骨上的水平羽毛控制迎角。
宽翼和短翼必须配备发达的端垫圈，以防止在机翼下方压缩的气流扩散到侧面。 此外，这些钉垫圈还可以用作降落的浮筒。

而且，在主翼末端需要附加的水平羽毛，以补偿垂直羽毛作用下的倾覆力矩。

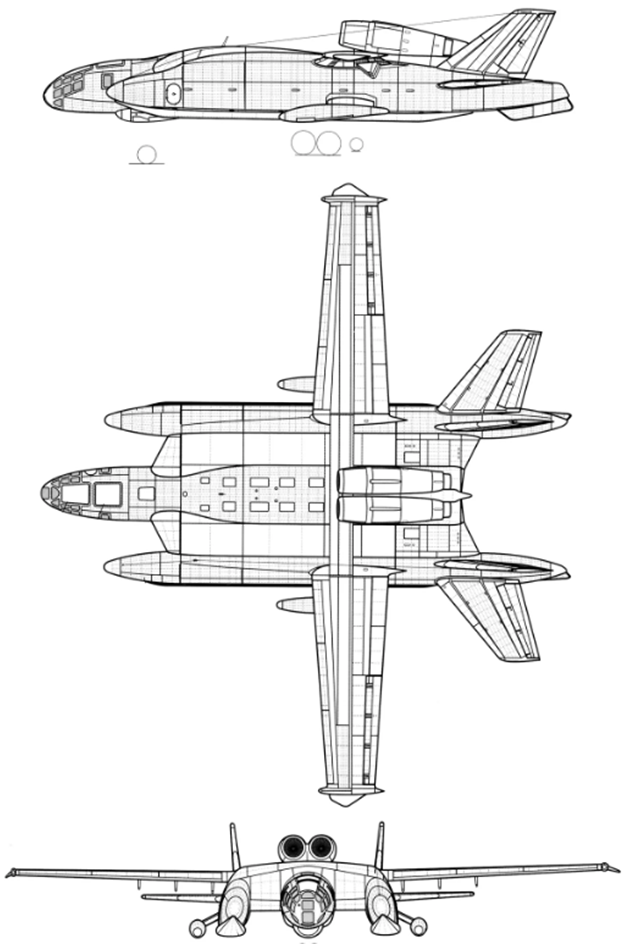
在实践中，WIG-VVA-14翼面飞机是根据这种方案（参见图9）和各种有前途的翼面飞机模型制造的，其中，端尾垫圈扮演着前垂直拖尾的角色（见图10）。


一个


b。


c。

图9 WIG Bartini VVA-14。 A.绘图。 b。 3D模型。 c。 当前样品在水面上的照片。



图10。 布局有希望的大型ekranoplan。

垂直羽化导致的ekranoplan操作类型：

• 两个相同间隔的龙骨提供“侧移”模式，并且可以在一个方向上同时旋转。 同时，机翼从一个车道移到另一个车道，而船体没有旋转。 在这种情况下，水平羽毛在不同的方向上起作用，以补偿垂直羽毛的横倾力矩。
• 如果龙骨以相同角度沿不同方向旋转，则会产生旋转力矩，使WIG车身绕垂直轴旋转。 在这种情况下，水平尾巴不起作用，因为不会发生来自垂直尾巴的力矩。
• 如果龙骨以不同的一致角度沿不同的方向旋转，则将沿圆形路径（循环）旋转，其中速度矢量与Ekranoplan机身纵轴的方向重合，并且Ekranoplan自身以相同的角速度飞过给定的圆形路径，并且Ekranoplan自身围绕周围旋转垂直轴。
  
  在这种情况下，水平羽毛在不同的方向上起作用，以补偿垂直羽毛的横倾力矩。

所有这些模式在手动模式下实际上都是不可行的，因为低海拔根本没有留出时间以人类的感知速度做出反应。 要控制ekranoplan，您需要控制自动化，类似于4-5代超不稳定战斗机的自动稳定功能。

结论

以上所有假设均基于公开发布的实验数据（机翼上的ADT压力图和其他数据）。

在过去的一个世纪中，已经在实验空气动力学上投入了大量资金，用于建造各种类型和尺寸的ADT，并且在各种飞机和单个机翼元件的模型试验中获得了大量的实际材料。

令人惊讶的是，在教学过程中，学生并不依赖于真实实验的材料，而是依赖于100年前的可疑理论。 而且尽管实验数据本身显然与这些生苔的理论相矛盾。

即使在诸如FALT FizTech的“空气动力学入门”这样的概括性入门课程中，也没有给出“机翼提升力”基本概念的定性解释模型，而是被具有数学公式的抽象科学方法（此外，不允许进行任何计算）取代。

在科学领域，在特定产品的开发中，理论与实际工程应用之间存在着分化的趋势。 理论模型中明显的矛盾并没有被宣告，而是相反地以各种方式保持沉默，以免动摇苔藓和已经去世的老人的权威，也不会打断他们在相当现代的教科书和专着中的真诚错误的胜利行进。

PS在本文的第一部分发表后，在文章下进行了讨论，当时剑桥大学的一位教授在那里讲授了“空气动力学”课程，当时发表了大致相同的想法。 在该消息中，有一个链接，该视频有一个教授在该主题上的演讲的视频，还有一个文章的链接，在该页面的最后一页描述了与弯曲空气形成压力的方法完全相同的方法，正如我在本文中所描述的那样。
我感到非常高兴的是，现在我不需要自己抵抗所有攻击，但是您可以参考2003年英国科学杂志上的剑桥教授及其文章。

这是带有链接的消息：
”
Joehopkins7
二月24，2019在22:35
-1
观看有关空气动力学的各种视频时，我偶然发现了剑桥教授关于空气动力学的有趣演讲。
早在2003年，一位剑桥教授在讲座中向学生讲解了与本文讨论的作者完全相同的想法。
我什至怀疑作者只是simply窃者。
但是，由于他在文章中没有提及英国科学家，也没有引用这些视频作为辩护，因此我们可以相信他诚实地独立发现了别人的发现。

这是讲座的链接
www.youtube.com/attribution_link?a=nfUWqs-6T7M&u=%2Fwatch%3Fv%3DH2RRiF24L4A%26feature%3Dshare&fbclid=IwAR2NOfdqNs0HK9WbCp-OYwy0Y4LYK0ajPPqq_qqp_qqpo

还有一篇文章的链接，其中早在2003年，剑桥大学的一位教授在英语科学期刊上写的东西与哈布雷的一篇文章的作者完全一样

www3.eng.cam.ac.uk/outreach/Project-resources/Wind-turbine/howwingswork.pdf
..“

机翼的升力。 第二部分

Monin Ilya Alekseevich博士，imoninpgd @ gmail.com

为了理解“航空”作为工业分支以及“空气动力学”作为科学的发展顺序，有必要回顾一下，首先出现了由热情的灵感工程师制造的第一架飞机（见图11），然后才出现了理论家，然后由理论家来创造。基于设计工程师创建结果的“空气动力学”学科。
在图片中，由驾驶人亨利·法曼（Henri Farman）制造的飞机是对Voisin小型飞机的改型。 同时，Voisin兄弟的最初飞机只在1907年才开始生产。 在购买Farman时，Voisin的飞机只能轻微反弹并飞行几十米。 在对原始飞机进行了一系列改装之后，法曼获得了飞过1000m的机会，同时仍在转身并绕圈着陆。 Farman的纪录飞行发生在1908年1月13日。 早在1909年，法曼兄弟公司就开始生产自己设计的飞机，并开设了飞行学校，向他们传授飞行技术（见图12）。 当时，法潘的飞行速度约为60 km / h，这在创纪录的180 km的飞行中得到了证明，在3小时的飞行中得以克服。



图11。 Voisin的飞机模型在1907-1908年被Farman改装成创纪录的飞行。




图12。 飞机“ Farman IV-1910”的布局。 在博物馆里，以及在机场的真实样本照片。

显然，最早的早期飞机是低功率，轻便和低速的。
这些参数对应于第一凸凹薄轮廓，更类似于最简单的弯曲胶合板，而不是具有深层理论错误计算的复杂轮廓。
作为参考，我举例说明了机翼轮廓从20世纪初到40年代中期全面发展的航空业的转变。 （见图13）



图13 20- .

. 薄的机翼无法承受需要在机翼内安装高强度横梁的任何规模和重量，机翼本身应制成平凸或什至双凸形，以将支撑梁隐藏在流线型机翼下摆的后面。
20- .
1940- , , . .
30- «», , ().

1939 ( ) -101, .
5–52 /
每1 m的重新编号为3.6∙106

1.7

(α) ±20°
(β) ±180°
:
() 24x14
24
:
: 18
: 30
: 35 2

, , -101 , .
, , , - 20- , . , 1980- (..14).


.14. « ».

, - 1960-80- (.15), 1930- (.16).
30- .
-25, 1933 , . , .
-25 , , . 4000 88., 50/., 500 104/ (29 /) . , ( ), -25 165/ (.246/ ), 10-12. 75-80 .

.
.
.

.15. « »: .) . .) . .) .

.
.


.16. - -20 « », 1939. ) . ) .

.

. , .
, , , .
, .
, . « » [3] (.435-437), , « » . « ». , ( ) - .
« ».
(..17), , .
, «» .
(..18), (..20).



.17. , .




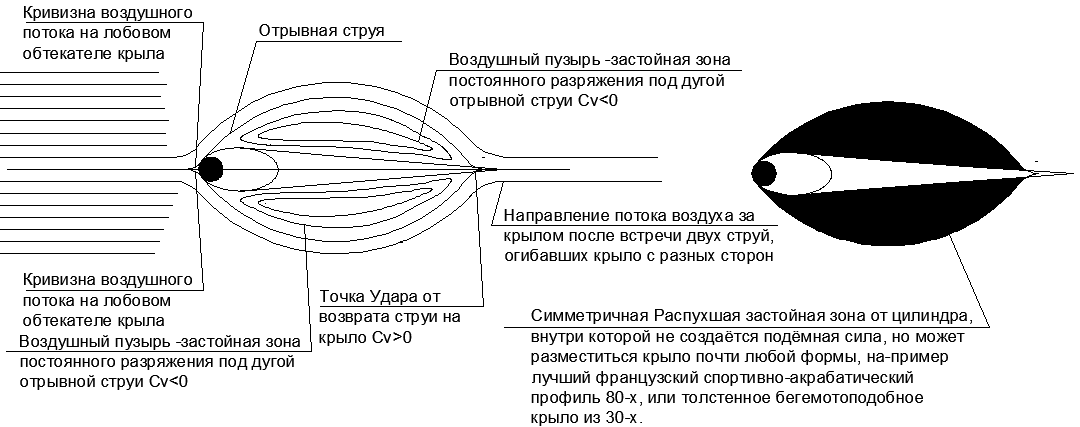.18. « ».

« » , -, .
=0,06, =0,4..0,5, =1.
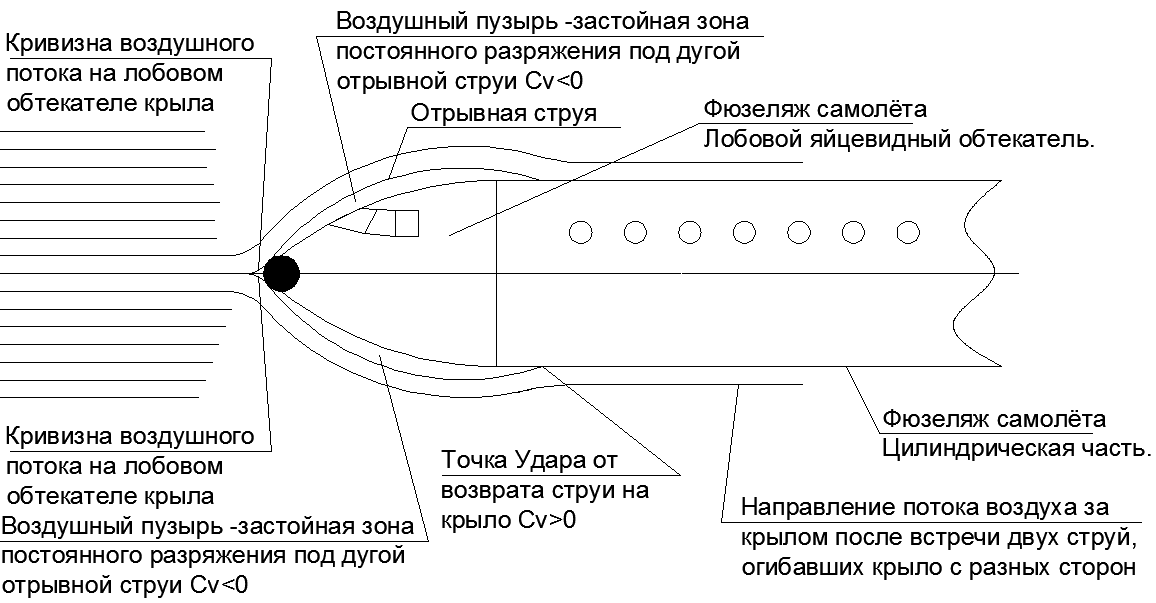
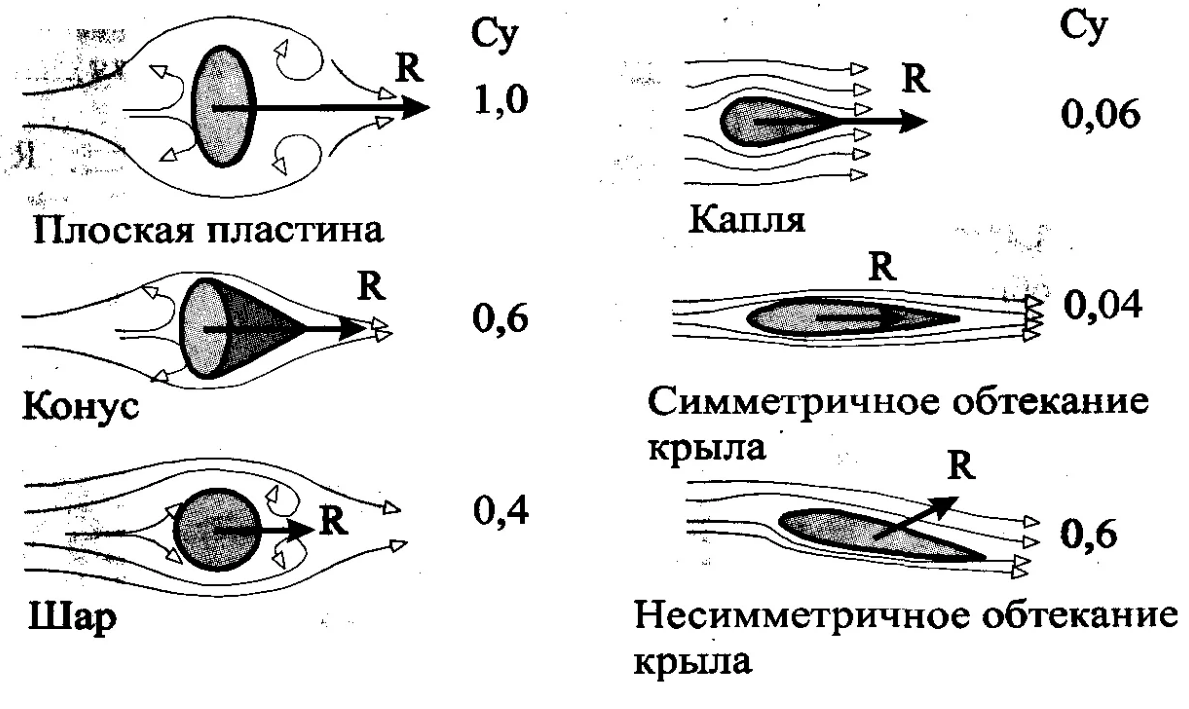
. , . . , (..19.)
, , , . « » . , .



图 19. , . . .

(..20).
. , , .
.
. « »= « » .
« » . , « » . (. .21)



.20. « ».






.21. . ( - ).

«» , , .
, , .
( 15 ), .
. - , « » «- ». , -20 « ».
( ) . « » , (..22).
(..22-2). www.youtube.com/watch?v=Sd4ycAtYcJA . .


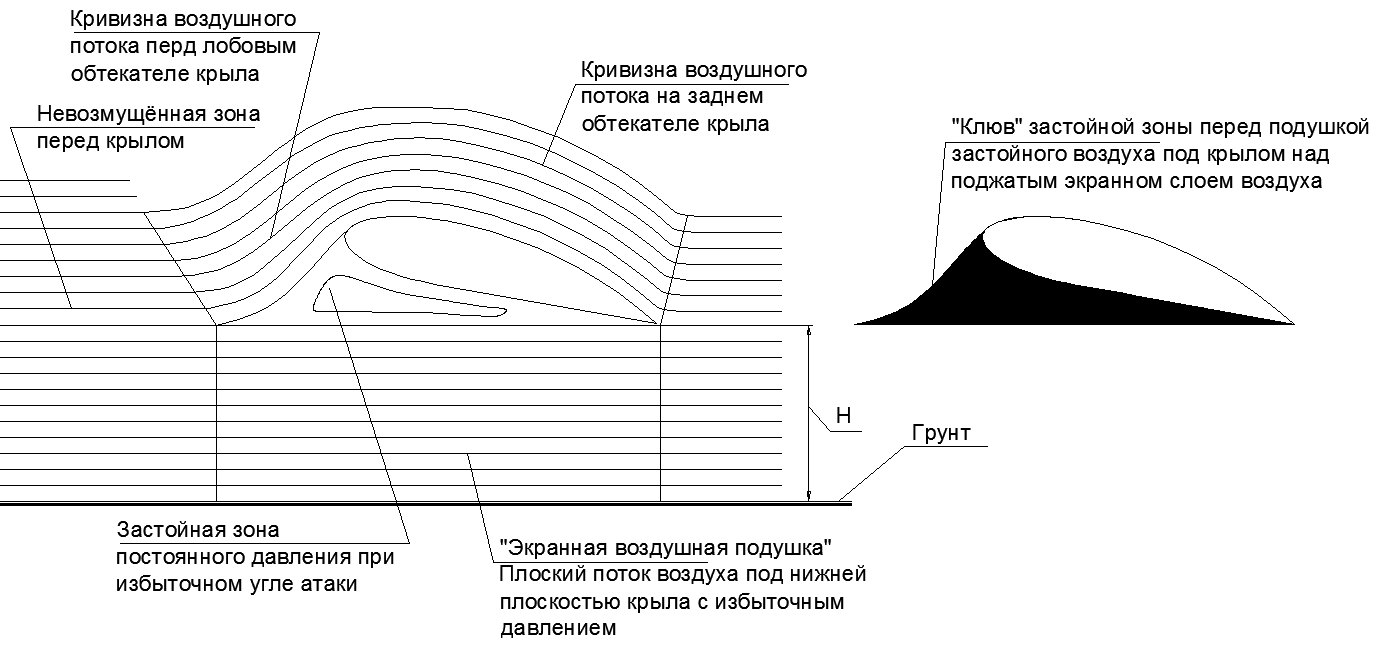.22. « ».


.22-2. , -747 .

-14 (), -20 « ».
1930- , -20 « ». , , (. .16.).
, 198/ ( 220/).
-20 , , « » .
« » 1930- « » 60- (..5)

.5. -20 « » 1934. « » 1966.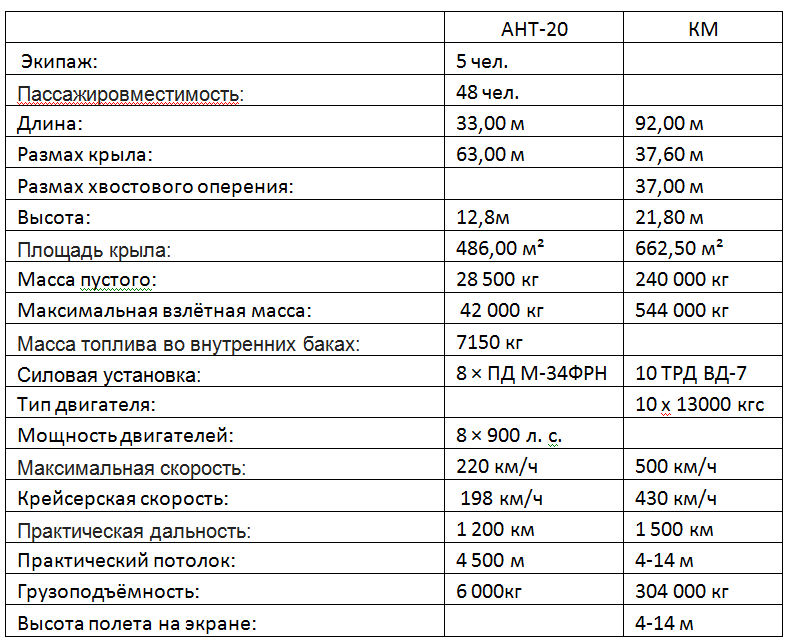


, - .
.
: 544/42= 13
: 662/486=1,36
: 13/1,36=9,5
: 430/198=2,17
: 2,17^2= 4,71
: (10*1300*9,81*430/3,6) /(8*900 000*0,735)=28,8
: 304/(42-28,5)= 22,51.
: 1500/1200=1,25
-20 = 7150/(1200*6)=0,993 /(*)
, .
0.8/(*) -7.
10*13000*0,8=104 000/
, .
2*13 000*0,8=20 800/
1500/430=3,5
1500 104*0.5+3,5*20,8=100 .
200 .
100 000/(1500*200)=0.333 /(.).

:
1. 3 , -20.
380 A380F 150 10 370 . — 560 ( — 280 ). 130 150 10370: 130000/(150*10370)=0,0835 /(*).
: « — (54 ) . Airbus[5], A380 17 % , « » ( , Boeing 747). „

850 .
, 4-5 80 , 10 -20 4 . 20 5 , -25. .
2. , . - « » > « »,
Pv= 8560 430/(120/) > 544000*9,81/662,5=8055.
3. 30年代以来的低速巨型飞机的飞行安全性比60年代以来的超高速有翼飞机的飞行安全性要好得多，几乎无法控制地冲向慢速航行的船只和无处不在的水鸟。
4.海上海基飞机的运营成本比陆地高空飞机的成本高得多。这是由于仅从水面出发并离开屏幕飞行所需的引擎数量过多，以及由于暴露于引擎时海水的极端侵蚀性以及由于附近海浪飞溅而在云层中飞行时产生的ekranoplan设计。
5. , =544/(13*2)=20,9. , =18-20.
6. 380F: 4 ?
?

. №3.

(4.02.2019) .
41 « », .
.
, , .

1.
, .
, - (.19 ) x.
, Cd, () .
Cd 0,27.
0,06..0,04, D .
, 0,06...0,04, , - . Cd (), C , .
, , «» «», .
d, “», c .

. d .
- . - .


2.
- - , «-», , , . .
-30 , .
, - .
« » .
« » - imoninpgd@gmail.com, .
.

.

, (..23, 24)
, , .
, , .
, . , .
, , , .



.23. , - .




.24. 3-.


(.25) «», .
- , 1- , «» 1- .
, , , , . .

, «» , «» «», «» «» .



.25. .

1930- , , - , .
, , «- », .
(. ) , .
, , , .
, ,
R=2*R.
R – .
= R.
, =48 .
V. =V* sin =0,743*V.
, R=2* =R.

..= V.^2*q*R
, .
= *
.=
V.^2*q* = *
:
= V.^2*q* R /
V. =V* sin :

= (V * sin )^2*q* R / = V.^2*q* sin ^2* R/
.
, , .
.
, , .
T=V /.
.=/(R*q)
T1=V /.= V *(R*q)/
L1
L1=V*1= V* V *(R*q)/ = V *(V * sin )*R*q/ =>
L1=V ^2*q * sin *R /
L1 ( ) , V R , L 1+2= 2* L1 .
, , .
. , .
(..26):
— , F1= F.- F., L1
— V , F2 F1. L2 .
— .
— .
- , , .
, , , .
, .
, , , , .
, .
.
, , , .
( ) .



.26. :
1) F1 , .
2) F2 . F2 L2 .
3) . - . F3 , .
4) , , , .

- V .
. « – » .
, , , .
«» «». «» «», .
, . .
, .
R, V .
, .
, , .
, ( ) .
, , « » .
, .
- , , .
.


R , .
1930- 300-400/, .
R , -3 1940.
, .
!
— «» «». , .
, .
-16 -3 ( ). 75-170 / ( 420/ 470/), , -3 ( 495/, 640/).
-3 -16 495/420=1,18.
, 20% 1,44 .
20% 1,5 , (, , ), .
-3, -16, .
2,5-3 , .
800-900/, V, . , , .
- .
… 1939 ( ) -101. , -101 , ( 52/ 187/) 1930-, . , .
(..27).
.
— — , . , . , -1 .
, , . (..28)


.27. . , . .




.28. ( — ). — . - 100%.

:

• « », .., , , 1986.-413.
• «» 1, .., , , 2018,-496.
• «», . .., , ...,2017,-607.