在2019年举行会议之后,除了为Smart IDReader开发新功能而休息了一点之后,我们还记得我们很长时间没有写任何有关家用处理器的文章了。 因此,我们决定紧急纠正并在Elbrus上显示另一个识别系统。
作为一种识别系统,绘画对象的识别系统被认为是“在不受控制的条件下,通过一个实例的方法进行训练” [1]。 该系统基于奇异点及其描述符建立图像描述,并在索引的图片数据库中进行搜索。 我们分析了该系统的性能,并确定了算法中最耗时的低级部分,然后使用Elbrus平台的工具对其进行了优化。
我们在谈论什么样的识别系统?
当前,大多数博物馆和美术馆使用各种工具来独立地熟悉展览会。 与经典的音频指南一起,使用图像处理和分析方法的移动应用程序也已广泛普及。 这些应用程序中的一些可以识别展览品的图形代码(条码或QR)[2],对于其他应用程序[3-4],输入数据是带有特写拍摄的展览品的照片或视频帧(Smartify,Artbit)。 当然,与手动输入展览品编号或QR识别的解决方案相比,后一类的``移动指南''对用户来说更方便[5]:数量和代码很小,其搜索和输入需要与展览会审核无关的其他操作。 我们将考虑的就是这样一个系统。
图像中识别绘画的任务规定如下。 索取图片 问 必须分配给其中一个类别 C = \ {C_i \} _ {i \ in [0,N]}C = \ {C_i \} _ {i \ in [0,N]} 在哪里 Ci -图片类 我 展览在 i in[1,N] , C0 -与“未知图片”值相对应的一类其他图像。 对于每个 Ci 参考图像集 Ti 。
此外,我们遵循以下假设:
- 索取图片 Q 因此,在旅途中,未经准备的用户使用移动设备的相机获取的信息是:
a)它可能包含视觉缺陷-强光,散焦的区域,噪音;
b)角度,取景框,照明和色彩平衡未知(图1a);
c)图片上可能存在异物,例如风景,相框,访客等(图1b)。 - 参考图片 T 它是具有图片的正面投影或其数字复制的高分辨率图像。 该标准不包含异物和视觉缺陷。 标准可以是,例如,定性扫描的艺术专辑页面(图2)。
- 图片(根据要求和标准)可以适用于任何样式-写实,
印象派,抽象派,分形图形等 - 班数 N 对应于收藏的大小,并且一个画廊可以达到
数十万个展品[6]。

图1-图像请求的示例a)在弱光下从远处拍摄照片,b)访客在框架中。

图2-绘画的参考图像示例a)克劳德·莫奈(Claude Monet),《韦斯特海姆(De Voorzaan en de Westerhem)》,b)萨尔瓦多·达利(Salvador Dali),《持久性记忆》
我们解决此问题的主要思想是基于从输入图像中对图片进行特殊描述的构造,然后将其用于在高分辨率绘画参考图像的描述数据库中搜索该图片,该参考图像的描述不受几何变形和其他照片缺陷的影响。 使用YACIPE算法[7]找到的奇异点的坐标及其RFD描述符就是这样的描述。
对于每个参考 Ti 建立一个描述,然后对其进行索引-对于描述中的每个点,我们都输入一个表格记录 langlei,fi rangle 到随机分层聚类搜索树[8]中,与线性搜索相比,该树可对具有最大速度增益的最近邻居执行近似搜索。 因为我们使用二进制描述符,所以将汉明距离用作度量。
识别过程如下:
在要求图片中 Q 绘画区 QL 使用框架矩形的假设进行预定位。 使用快速四边形搜索算法[9]进行区域搜索,消除了长宽比的限制。 这样可以防止出现以下问题:
-画面中由于异物而对图像区域的描述不足,这些异物可能具有评分最高的特殊点;
-用于比较图片外部区域描述符的计算成本;
-数据库中的标准与图片的图片之间在比例尺和角度上的严重不匹配,这导致匹配描述符的结果不正确。
找到区域中的图像投影归一化:
Q∗=H(QL),
在哪里 H -投影变换。
建立一个简短的描述 w∗ :
a)在保持比例的同时将图像缩小到标准尺寸,以使算法对缩放更具弹性;
b)用高斯滤波器抑制高频噪声;
c)在结果图像上计算出奇异点,其数量被人为限制为 M 通过YACIPE内部评估获得最佳结果;
d)计算发现的奇异点附近颜色的类似于RFD的描述符,因为在我们的任务中,重要的是保存有关输入图像颜色特征的信息。 例如,图中的图片。 3如果没有它,将很难区分;
d)因此,图像的描述 我 可以表示为: w ^ * = \ {\ langle p_i,f_i)\ rangle \} _ {i \ in [1,M]} 在哪里 pi= langlexi,yi rangle 是第i个奇点的坐标,并且 fi 是第i个奇异点附近的句柄。
对于每个条目 langlep,f rangle inw∗ 索引对描述符的最近邻居执行近似搜索 f 。 投票程序应用于找到的描述符-描述符 fi 向标准添加声音 Ti 。 然后,选择具有最高投票数的K个候选候选人。
对于每个 K 使用RANSAC算法选择选项,执行投影变换搜索 H 在给定的几何误差内进行翻译 delta 查询点 Q∗ 参考点 T 。 对点 langlep,p′ rangle 如果满足以下条件,则具有近似描述符的字符被视为有效匹配:
\左|H(p)−p′\对|< delta,p inw∗,p′ inwT
最终结果是选择了标准 Tb 正确比较的数量被证明是最大的。 如果小于某个阈值 R ,结果将是答案“未知图片”,以避免误报(例如,在搜索数据库中没有标准描述的图片中)。


图3-莫奈(Claude Monet)。 鲁昂大教堂,西立面,阳光(左)和鲁昂大教堂,门户和圣罗曼塔在阳光下(右)。
系统的主要部分之一是使用汉明距离作为度量标准来搜索接近的描述符。 由于它需要多次计算,因此此阶段需要大量的计算时间,并占用系统时间的65%。 这就是我们对其进行优化的原因。
对Elbrus架构的很小描述
Elbrus的处理器体系结构使用宽命令字(Very Long Instruction Word,VLIW)的原理。 这意味着处理器按组执行指令,并且在每个组内没有依赖关系,并且这些指令并行执行。 每个这样的组称为广义命令字。 宽泛的命令字由优化的编译器生成,这使得对源代码进行更详细的分析成为可能,从而导致更有效的并行化[10]。
Elbrus体系结构的一个特点是使用内存的方法。 除具有优化内存访问时间的缓存外,Elbrus处理器还支持用于预分页数据的硬件-软件方法。 这种方法可以预测内存访问并将数据泵入初步数据缓冲区。 处理器的硬件包括用于访问阵列的特殊设备(阵列访问单元,AAU),但是交换的需要由编译器确定,编译器会生成AAU的特殊指令。 使用交换设备比将数组元素放入缓存更有效,因为数组元素最常按顺序处理,很少使用一次以上[11]。 但是,应该注意的是,仅当使用对齐的数据时,才可能在Elbrus上使用预分页缓冲区。 因此,读取/写入对齐数据的速度比未对齐数据的相应操作快得多。
此外,除命令级别的并行性外,Elbrus处理器还支持多种类型的并行性:SIMD并行性,控制流并行性,多机组合系统中任务的并行性。 我们特别感兴趣的是SIMD并发。
使用SIMD扩展处理器Elbrus的功能
SIMD扩展的使用可以通过两种模式进行:自动和直接。 在第一种情况下,操作的并行化完全由编译器执行,而无需开发人员的参与。 此模式是有限制的,因为优化的代码必须完全重复源代码的行为,包括溢出,舍入等时的行为。 在这种情况下,SIMD扩展指令的行为在这些方面可能与处理器指令有所不同。 另外,在编译器中使用的算法是不完善的,并不总是能够执行有效的并行化。 但是,开发人员也可以使用内部函数直接访问SIMD扩展命令。 内部函数是函数,其调用被编译器替换为给定平台的高性能代码,尤其是SIMD扩展命令。 Elbrus-4C和Elbrus-8C处理器支持一组内部函数,其寄存器大小为64位。 它包括数据转换操作,矢量元素初始化,算术运算,按位逻辑运算,矢量元素置换等。
在Elbrus平台上使用内在函数时,应特别注意对内存的访问,因为实际任务(例如图像处理任务)通常需要将数据不平衡地读取到64位寄存器中。 这种读取本身效率低下,因为它需要一对读取命令和一个后续命令来形成数据块,但是更重要的是,不能使用数组交换缓冲区来提高数据访问速度。 但是,值得注意的是,对于Elbrus-4C和Elbrus-8C处理器,访问未对齐数据的效率低下的问题是相关的,而对于具有第5版指令系统的较新的Elbrus-8CV,则可以部分解决。 预计带有第六版指令系统的Elbrus处理器将被完全解决。
但是,在Elbrus-4C和Elbrus-8C处理器上,考虑到对齐方式,可以有效地执行低级数据处理。 例如,对于数字数组,它可以包括几个阶段:处理初始部分(直到其中一个数组的64位对齐边界),使用对齐的内存访问处理主要部分以及处理数组的其余元素。 由于在编译过程中解析指针并非易事,因此可以使用–faligned编译器–faligned ,通过该–faligned ,所有内存访问操作均以对齐方式执行。
在Elbrus平台上使用内在函数的下一个功能与其VLIW架构直接相关。 由于存在多个并行运行并在形成宽命令字时加载的算术逻辑设备(ALU),因此可以同时执行多个命令。 总体而言,Elbrus-4C和Elbrus-8C处理器具有六个ALU,可以用作一个广泛的团队的一部分,但是每个ALU支持自己的一组内在函数。 通常,简单的操作(例如在64位寄存器中增加或增加元素)支持两个ALU。 这意味着Elbrus处理器可以在一个时钟周期内执行两条这样的指令。 为此,应在可执行代码中使用运行循环。 Elbrus平台的优化编译器支持pragma #pragma unroll(n) ,它允许部署n个循环迭代。
考虑到这些功能的加法功能的实现示例可以在我们以前的文章中找到。
实验
好的,文本结束了,最后我们将在Elbrus上发布一些东西!
首先,我们分别考虑汉明距离。 事不宜迟,我们比较了随机数据的两个位向量。 二进制值打包成8位整数的数组,为简单起见,我们认为原始向量的长度是8的倍数。通常,该代码是用C ++编写的,由lcc 1.21.24(一种经过优化的Elbrus编译器)编译。
我们编写了汉明距离的几种实现,依次考虑了Elbrus处理器的功能。 他们看起来像这样:
- 使用8位整数与预先计算的值表之间的按位XOR。 这是一个基本的实现,没有任何固有的技巧。
- 它使用32位整数与内部函数之间的XOR来计算32位整数-popcnt32中的单位数。 未执行32位边界对齐。
- 它使用64位整数与内部函数之间的XOR来计算64位整数-popcnt64中的单位数。 未执行64位边界对齐。
- 它使用64位整数与内部函数之间的XOR来计算64位整数-popcnt64中的单位数。 对内存的访问以对齐方式进行。 由于阵列的起始地址可以具有不同的对齐方式,因此在读取阵列之一时,将读取两个相邻的64位块,并从中形成必要的64位块。
- 它使用64位整数与内部函数之间的XOR来计算64位整数-popcnt64中的单位数。 对内存的访问以对齐方式进行。 由于阵列的起始地址可以具有不同的对齐方式,因此在读取阵列之一时,将读取两个相邻的64位块,并从中形成必要的64位块。 另外,使用
-faligned编译器标志。 - 它使用64位整数与内部函数之间的XOR来计算64位整数-popcnt64中的单位数。 对内存的访问以对齐方式进行。 由于阵列的起始地址可以具有不同的对齐方式,因此在读取阵列之一时,将读取两个相邻的64位块,并从中形成必要的64位块。 此外,还使用了
-faligned编译器-faligned和编译器编译指示#pragma unroll(2) (以使用两个可用的ALU来计算popcnt64)和#pragma loop count(1000) (以启用其他#pragma loop count(1000)优化)。
时间测量的结果示于表1。
表1.在配备Elbrus-4C处理器的机器上,计算长度为10 ^ 5的两个打包二进制数字数组之间的汉明距离的时间。 平均时间超过10 ^ 5开始。
| 不行 | 实验 | 时间,毫秒 |
|---|
| 1个 | 计算值表 | 141.18 |
| 2 | popcnt32,不对齐 | 125.54 |
| 3 | popcnt64,不对齐 | 58.00 |
| 4 | popcnt64对齐 | 17.36 |
| 5 | popcnt64对齐, -faligned | 17.15 |
| 6 | popcnt64,对齐方式, -faligned, pragma unroll | 12.23 |
可以看出,所有考虑的优化导致运行时间减少了11.5倍。 值得注意的是,对内存的不平衡访问使用内在函数时,加速度仅是1.13倍(对于popcnt32)和2.4倍(对于popcnt64),而考虑到数据对齐导致使用了APB阵列交换缓冲区借助它,可以实现另外3.4倍的加速(58 ms对17.15 ms)。 尽管在上面的示例中使用-faligned标志并未显示出明显的性能提升,但是在更复杂的算法中,可能会出现编译器无法深入分析源代码以生成APB命令的情况。 考虑到专用ALU的实际数量,我们可以将计算速度再提高1.4倍。
还不错! 由于我们比较了多达6个实现选项,因此我们给出了最终最快的伪代码:
: 8- A B, T, T[i] i : res, A B offset ← A 64- effective_len ← , 64- for i from 1 to offset: res ← res + T[xor(A[i] , B[i])] v_a ← 64- , A[offset+1] v_b1 ← 64- , B[offset] v_b2 ← 64- , v_b1 // 64- for i from offset to effective_len: v_b ← align(v_b1, v_b2) // 64- , v_a res ← res + popcnt64(xor(v_a, v_b)) v_a ← 64- v_b1 ← v_b2 v_b2 ← 64- //
一劳永逸地将汉明距离的计算速度提高11.5倍,那将是一件很棒的事,但是生活中的一切都有些复杂:只有在数组长度足够大的情况下,这种实现方式才有优势。 在图 图4给出了使用预计算值表和我们最终实现的计算时间的比较。 您可以看到,在我们的版本中,它仅在长度超过400字节时才开始取胜,并且在Elbrus上进行优化时也需要考虑这一点。
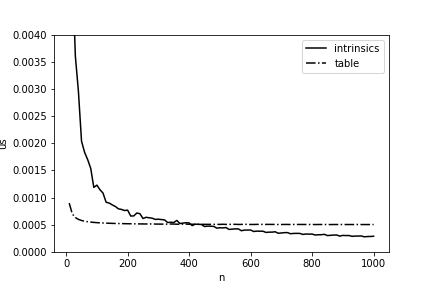
图4-根据两个数组在Elbrus-4C处的长度来计算两个数组之间的汉明距离的平均时间(每1个字节)。
就是这样,现在我们可以测量整个系统的运行时间了。 我们测量了933个请求的平均请求处理时间(不包括图像加载)。 编译图像的紧凑描述时,使用了5328位彩色的类似于RFD的二进制描述符。 它由为输入图像部分的每个通道计算的3个串联的1776位灰度RFD描述符组成。 一方面,如此长的描述符对高速的计算和比较不满意;另一方面,它们提供了足够高的工作质量。 但是,有个好消息-我们可以使用汉明距离的快速实现来进行比较! 比较数组的长度为666字节,大于Elbrus-4C的阈值400字节。
测量结果如表2所示。可以看出,只有一种快速实施汉明距离的方法,查询处理速度才能提高1.5倍。 还值得注意的是,这种优化不会改变计算结果,因此不会改变识别质量。
表2.在不受控制的条件下对绘画对象识别系统的请求的平均处理时间。
| 实验 | 请求时间,s | 海明距离的计算 | 加速时间 |
|---|
| 基本实施 | 2.81 | 63% | -- |
| 快速实施 | 1.87 | 40% | 1.5 |
结论
在本文中,我们讨论了用于在不受控制的条件下绘画对象的识别系统的结构,并再次展示了低级操纵如何显着提高Elbrus平台上的速度。 因此,建议的汉明距离实现比使用具有足够大的输入矢量长度的预先计算值表的实现快一个数量级(!),并且整个系统的速度提高了一半! 为了获得此结果,使用了SIMD扩展,并考虑了Elbrus-4C和Elbrus-8C处理器的体系结构和内存访问功能。 这些结果表明,Elbrus处理器包含大量资源,用于高效运行,如果没有专门执行的优化,这些资源将无法充分利用。 但是,预计将在较新的Elbrus处理器上改进内存访问方法,这将允许其中一些优化自动执行,并极大地延长了开发人员的生命。
文学作品
[1] N.S. A.N. Skoryukina Milovzorov,D.V. 菲尔德 阿拉扎罗夫。 根据一个示例// ISA RAS的交易通过训练识别在不受控制的条件下绘画对象的方法。 -特刊,2018-p。 5-15。
[2]Pérez-SanagustínM.等。 使用QR码增加用户在类似博物馆的空间中的参与度//人类行为中的计算机。 -2016.-T. 60.-S. 73-85。 doi:10.1016 / j.chb.2016.02.02.012
[3] Antoshchuk S. G.,Godovichenko N. A.在“移动虚拟向导”系统中对图像的点特征的分析// Pratsi。 -2013年-没有 1(40)。 -S. 67-72。
[4] Andreatta C.,Leonardi F.移动博物馆指南的基于外观的绘画识别//国际计算机视觉理论与应用大会,VISAPP。 -2006年。
[5]伦纳德·温。 2014.博物馆指南应用程序中的视觉识别:参观者想要吗?..在SIGCHI关于计算机系统人为因素会议(CHI '14)的会议记录中。 美国纽约州ACM,电话:635-638。
doi:10.1145 / 2556288.2557270
[6]特列季亚科夫画廊, https: //www.tretyakovgallery.ru/collection/
[7] Lukoyanov A. S.,Nikolaev D. P.,Konovalenko I. A. YAPE算法的修改,用于具有较大局部对比度的图像//信息技术和纳米技术。 -2018年-S.1193-1204。
[8] Muja M.,Lowe DG二元特征的快速匹配//计算机和机器人视觉(CRV),2012年第九届会议开始。 -IEEE,2012年。-S. 404-410。
doi:10.1109 / CRV.2012.60
[9] Skoryukina,N.,Nikolaev,DP,Sheshkus,A.,Polevoy,D。(2015年2月)。 移动设备上的实时矩形文档检测。 第七届机器视觉国际会议(ICMV 2014)(第9445卷,第94452A页)。 国际光学和光子学会。
doi:10.1117 / 12.2181377
[10] Kim A.K.,Bychkov I.N. 以及用于个人计算机,服务器和超级计算机的其他俄罗斯技术“ Elbrus” //现代信息技术和IT教育,M .:互联网媒体发展基金会,IT教育,潜在的“互联网媒体联盟”,2014年,第10页,第10页。 39-50。
[11] Kim A.K.,Perekatov V.I.,Ermakov S.G. 微处理器和计算系统
Elbrus一家。 -圣彼得堡:彼得,2013年。-272 S.