Geekly articles weekly

PageRank的工作原理：通过线性代数和幂方法在R中实现

您好，哈布罗夫斯克市民！

我叫亚历克斯。 这次我从ITAR-TASS的工作场所播出。

在此简短的文本中，我将使用R语言的简单易懂的示例向您介绍计算PageRank©的方法（以下将其称为PR） 该算法是Google的知识产权，但是由于其对数据分析任务的实用性，因此使用了许多任务，可以简化为在图中搜索大型节点并按重要性对其进行排名。

在帖子中提及大公司不是广告。

由于我不是专业的数学家，因此我使用-并向您推荐- 本文和本教程作为指南。

对PR的直觉理解


了解其工作原理并不困难。 有一组相互关联的元素。 它们之间是如何精确连接的-这是一个广泛的问题：也许通过链接（例如Google），也许通过彼此提及（几乎相同的链接），元素之间的转换概率（马尔可夫过程的矩阵）可以是先验指定的，而无需指定实体交流的意义。 我想为这些元素分配一定的重要性标准，该标准将包含有关在扩散过程中穿过该图的某些抽象粒子访问该元素的可能性的信息。

嗯，听起来不太清楚。 想象一个人使用带有罂粟花的笔记本电脑，浏览搜索结果页面，抽水烟，跟随一页到另一页的链接，并且越来越多的人出现在同一页（或多页）上，这更容易想象。

这是由于以下事实：他访问的某些页面在原始来源中包含了如此有趣的信息，以至于其他页面被迫使用链接的指示重新打印该页面。

Google中的这样一个人被称为随机冲浪者。 他是扩散过程中的粒子：图形上位置随时间的离散变化。 并且他以趋于无穷大的扩散时间访问页面的概率为PR。

PR计算的简单实施


我们同意-我们在如此小巧，舒适的小图中使用了10个元素。

# clear environment rm(list = ls()); gc() ## load libs library(data.table) library(magrittr) library(markovchain) ## dummy data number_nodes <- 10 node_names <- letters[seq_len(number_nodes)] set.seed(1) nodes <- sapply( seq_len(number_nodes), function(x) { paste( c( node_names[-x] , sample(node_names[-x], sample(1:5, 1), replace = T) ) , collapse = ' ' ) } ) names(nodes) <- node_names print( paste(nodes, collapse = '; ') ) ## make long dt dt <- data.table( citing_node = node_names , cited_node = nodes ) %>% .[, .(cited_node = unlist(strsplit(cited_node, ' '))), by = citing_node] %>% dcast( . , cited_node ~ citing_node , fun.aggregate = length ) dt apply(dt[,-1,with=F], 2, sum) ## affinity matrix A <- as.matrix(dt[, 2:dim(dt)[2]]) A <- sweep(A, 2, colSums(A), `/`) A[is.nan(A)] <- 0 rowSums(A) colSums(A) mark <- new("markovchain", transitionMatrix = t(A), states = node_names, name = "mark") plot(mark)

10个元素（节点）中的每一个都包含10到14个以随机顺序引用其他节点的引用（不包括其自身）。 目前，我们仅确定所提到的数据是Web链接。

显然，可能会出现某些元素比其他元素被提及更多的情况。 检查一下。
顺便说一句，我建议使用data.table包进行实验。 结合tidyverse原理，一切都变得高效而迅速。


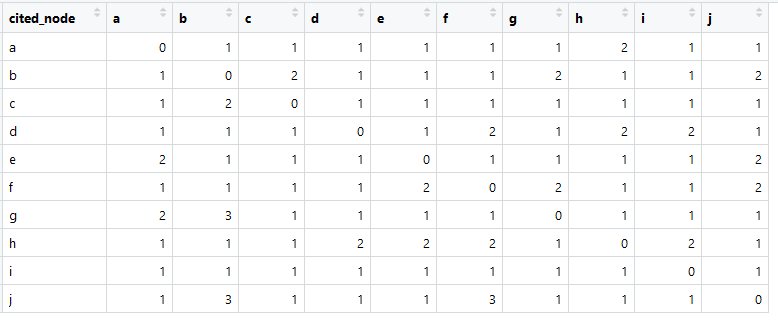
这就是我们的链接矩阵的外观（在英语中通常称为邻接矩阵）。

每列中的总和大于零，这意味着每个元素与某个其他元素之间存在联系（这对于进一步分析很重要）。
>适用（dt [，-1，带= F]，2，和）
abcdefghij
11 14 10 10 11 13 11 11 11 12

基于此表，我们可以创建所谓的“亲和力矩阵”，或者在我们看来，是邻近矩阵（也称为过渡矩阵），数学家将其称为随机矩阵（列-随机矩阵）： 主要来源

将其分配给名为A的变量。



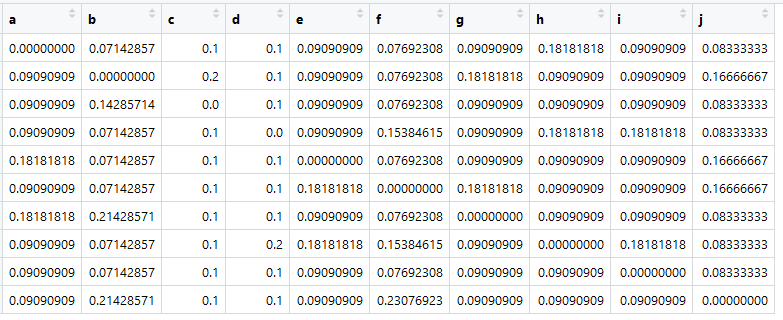
现在最重要的是所有列的总和等于一。
> colSums（A）
abcdefghij
1 1 1 1 1 1 1 1 1 1

这里是-过渡矩阵，它是马尔可夫，这是相似之处。 图是从列中的元素到行中的元素的转换概率。

当然，这些并不是真正的“相似之处”。 例如，如果我们计算文档显示之间的角度的余弦值，则将是当前值。 但是重要的是，将转换矩阵简化为（伪）概率，以使每一列的总和等于1。

让我们看一下马尔可夫过渡图（我们的A）：



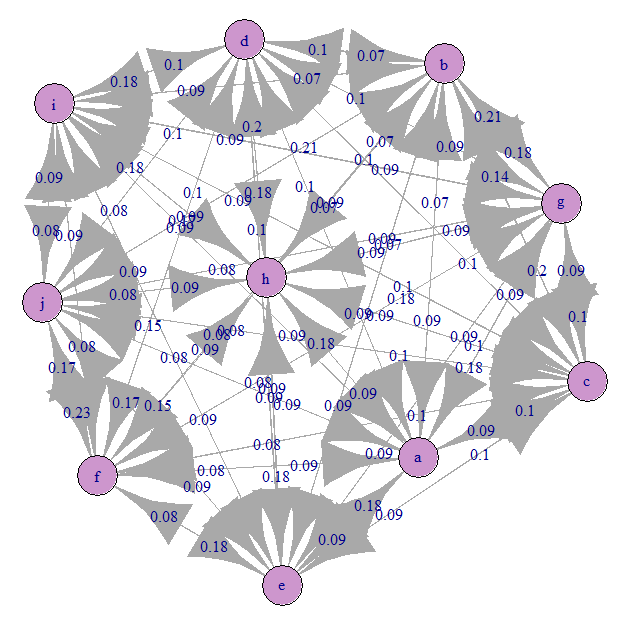
一切都几乎均匀地混淆了）。 这是因为我们指定了等概率转移。

现在是魔术的时候了！

 ## calculate pagerank ei <- eigen(A) as.numeric(ei$values[1]) pr <- as.numeric(ei$vectors[,1] / sum(ei$vectors[,1])) sum(pr) names(pr) <- node_names print(round(pr, 2))

对于随机矩阵A，第一个特征值应等于1，并且对应的特征向量是PageRank向量。
>打印（圆形（pr，2））
abcdefghij
0.09 0.11 0.09 0.10 0.10 0.11 0.10 0.11 0.08 0.11

这是PR值的向量-这是转换矩阵A的归一化特征向量，与该矩阵的等于1的特征值相对应-主导特征向量。

现在您可以对元素进行排名。 但是由于实验的特点，它们的重量非常相似。

使用幂方法的问题及其解决方案


转移矩阵A可能不满足随机性条件。

首先，可能有些元素在任何地方都没有引用，也就是说，没有反馈（它们可以自己引用它们）。 对于大型实图，这可能是个问题。 这意味着矩阵的一列将只有零。 在这种情况下，通过特征向量的解将不起作用。

Google通过用均匀概率分布p = 1 / N填充一列来解决此问题。 其中N是所有元素的数量。

 dim.1 <- dim(A)[1] A <- as.data.table(A) nul_cols <- apply(A, 2, function(x) sum(x) == 0) if( sum(nul_cols) > 0 ) { A[ , (colnames(A)[nul_cols]) := lapply(.SD, function(x) 1 / dim.1) , .SDcols = colnames(A)[nul_cols] ] } A <- as.matrix(A)

其次，图可能包含彼此反馈的元素，但不包含图的其余元素。 由于违反假设，这对于线性代数也是不可克服的问题。

通过引入一个称为阻尼因子的常数来解决该问题，该常数指示从任何元素到任何其他元素过渡的先验概率，即使没有物理链接也是如此。 换句话说，在任何状态下扩散都是可能的。

 d = 0.15 #damping factor (to ensure algorithm convergence) M <- (1 - d) * A + d * (1 / dim.1 * matrix(1, nrow = dim.1, ncol = dim.1)) # google matrix

如果我们将这些转换应用于矩阵，则可以再次通过特征向量求解！

第三，角质矩阵可能不是正方形，但这很关键！ 我不会在这一刻详述，因为我相信您自己会解决的。

但是，有一种更快，更准确的方法，在内存中也更经济（这可能与大型图有关）：幂方法。

 ## pagerank function (tested on example from tutorial) rm(pagerank_func) pagerank_func <- function( A #transition matrix , eps = 0.00001 #sufficiently small error , d = 0.15 #damping factor (to ensure algorithm convergence) ) { dim.1 <- dim(A)[1] A <- as.data.table(A) nul_cols <- apply(A, 2, function(x) sum(x) == 0) if( sum(nul_cols) > 0 ) { A[ , (colnames(A)[nul_cols]) := lapply(.SD, function(x) 1 / dim.1) , .SDcols = colnames(A)[nul_cols] ] } A <- as.matrix(A) M <- (1 - d) * A + d * (1 / dim.1 * matrix(1, nrow = dim.1, ncol = dim.1)) # google matrix rank = as.numeric(rep(1 / dim.1, dim.1)) ## iterate until convergence while( sum( (rank - M %*% rank) ^ 2 ) > eps ) { rank <- M %*% rank } return(rank) } pr2 <- pagerank_func(A) pr2=as.vector(pr2) names(pr2)=node_names

瞧！
>打印（圆形（pr，2））
abcdefghij
0.09 0.11 0.09 0.10 0.10 0.11 0.10 0.11 0.08 0.11
>打印（圆形（pr2、2））
abcdefghij
0.09 0.11 0.09 0.10 0.10 0.11 0.10 0.11 0.08 0.11

关于这一点，我将结束本教程。 希望您觉得它有用。

我忘了说，要构建一个转换矩阵（概率），您可以使用文本的相似性，引用的数量，链接的事实以及其他导致伪概率或概率的度量。 一个相当有趣的示例是在单词袋tf-idf的相似度矩阵上的文本中句子的排名，以突出显示总结整个文本的句子。 PR可能还有其他创造性用途。

我建议您自己尝试使用过渡矩阵，并确保获得很酷的PR值，这也很容易解释。

如果您发现我的不正确之处或错误，请在评论或消息中指出，然后我将予以纠正。

所有代码都在这里编译：

代号
 # clear environment rm(list = ls()); gc() ## load libs library(data.table) library(magrittr) library(markovchain) ## dummy data number_nodes <- 10 node_names <- letters[seq_len(number_nodes)] set.seed(1) nodes <- sapply( seq_len(number_nodes), function(x) { paste( c( node_names[-x] , sample(node_names[-x], sample(1:5, 1), replace = T) ) , collapse = ' ' ) } ) names(nodes) <- node_names print( paste(nodes, collapse = '; ') ) ## make long dt dt <- data.table( citing_node = node_names , cited_node = nodes ) %>% .[, .(cited_node = unlist(strsplit(cited_node, ' '))), by = citing_node] %>% dcast( . , cited_node ~ citing_node , fun.aggregate = length ) dt apply(dt[,-1,with=F], 2, sum) ## affinity matrix A <- as.matrix(dt[, 2:dim(dt)[2]]) A <- sweep(A, 2, colSums(A), `/`) A[is.nan(A)] <- 0 rowSums(A) colSums(A) mark <- new("markovchain", transitionMatrix = t(A), states = node_names, name = "mark") plot(mark) ## calculate pagerank ei <- eigen(A) as.numeric(ei$values[1]) pr <- as.numeric(ei$vectors[,1] / sum(ei$vectors[,1])) sum(pr) names(pr) <- node_names print(round(pr, 2)) ## pagerank function (tested on example from tutorial) rm(pagerank_func) pagerank_func <- function( A #transition matrix , eps = 0.00001 #sufficiently small error , d = 0.15 #damping factor (to ensure algorithm convergence) ) { dim.1 <- dim(A)[1] A <- as.data.table(A) nul_cols <- apply(A, 2, function(x) sum(x) == 0) if( sum(nul_cols) > 0 ) { A[ , (colnames(A)[nul_cols]) := lapply(.SD, function(x) 1 / dim.1) , .SDcols = colnames(A)[nul_cols] ] } A <- as.matrix(A) M <- (1 - d) * A + d * (1 / dim.1 * matrix(1, nrow = dim.1, ncol = dim.1)) # google matrix rank = as.numeric(rep(1 / dim.1, dim.1)) ## iterate until convergence while( sum( (rank - M %*% rank) ^ 2 ) > eps ) { rank <- M %*% rank } return(rank) } pr2 <- pagerank_func(A) pr2=as.vector(pr2) names(pr2)=node_names print(round(pr, 2)) print(round(pr2, 2))


PS：整个想法也很容易用其他语言实现，至少在Python中，我所做的一切都没有困难。

Source: https://habr.com/ru/post/zh-CN439332/

More articles:


All Articles