✋🏽 📝 🏂🏽 强化深度学习：原始像素乒乓球 🔂 🧚 👨‍🎓

这是一篇有关“强化学习”（RL）的早就应该发表的文章。 RL是一个很酷的话题！

您可能知道，计算机现在可以自动学习玩ATARI游戏（通过在入口获得原始游戏像素！）。他们在围棋比赛中击败了世界冠军，虚拟的四足动物学会了跑步和跳跃，机器人学会了执行复杂的操纵任务，这些挑战挑战了显式编程。事实证明，没有RL，所有这些成就都是不完整的。过去一年中，我对RL也很感兴趣：我与Richard Sutton的书（大约参考：已替换）一起工作，阅读了David Silver的课程，参加了John Schulman的讲座，编写了关于Javascript的RL库，并于夏天在DeepMind进行了实习， DeepRL是OpenRL Gym的最新开发工具，是OpenAI Gym的最新开发工具。因此，我当然已经参加了至少一年的浪潮，但仍然没有费心去写关于RL为什么如此重要，它是什么意思以及它如何发展的注释。

使用深度Q学习的示例。 从左到右：神经网络扮演ATARI，神经网络扮演AlphaGo，机器人折叠乐高玩具，虚拟四足动物围绕虚拟障碍物奔跑。

反思RL近期进展的性质很有趣。我想指出影响AI发展的四个独立因素：

计算速度（GPU，ASIC专用设备，摩尔定律）
可用形式的足够数据（例如ImageNet）
算法（研究和思路，例如backprop，CNN，LSTM）
基础架构（Linux，TCP / IP，Git，ROS，PR2，AWS，AMT，TensorFlow等）。

就像在计算机视觉中一样，RL的进步也在不断发展……尽管看起来并不像看起来那么快。例如，在计算机视觉中，AlexNet 2012神经网络是1990年代ConvNets神经网络的深度和宽度版本的增加。同样，ATARI Deep Q-Learning 2013是标准Q-Learning算法的实现，您可以在Richard Sutton的1998年经典著作中找到它。此外，AlphaGo使用策略梯度技术，而蒙特卡洛树搜索（MCTS）也是旧思想或其组合。当然，要使它们起作用，需要大量的技能和耐心，并且已经在旧算法的基础上开发了许多棘手的设置。 但大致上，近期进展的主要驱动力不是新的算法和思想，而是计算量的增加，足够的数据和成熟的基础架构。

现在回到RL。许多人无法相信我们可以教计算机如何使用从头开始的原始像素并使用相同的自学习算法来在人类水平上玩ATARI游戏。同时，每次我感觉到差距–看起来多么神奇，以及它真正的内在多么简单。

我们使用的基本方法实际上很愚蠢。尽管如此，我想向您介绍Policy Gradient（PG）技术，这是目前解决RL问题的我们最喜欢的默认选择。您可能很好奇，为什么我无法想象DQN，DQN是一种替代且知名度更高的RL算法，也用于ATARI训练中。事实证明，尽管Q学习是众所周知的，但它并不是那么完美。大多数人都选择使用Policy Gradient，包括原始DQN文章的作者，他们已经表明，通过良好的调整，Policy Gradient的性能甚至优于Q-Learning。 PG更可取，因为它很明确：有明确的政策和连贯的方法可以直接优化预期的回报。例如，我们将学习如何玩ATARI Pong：从头开始，从原始像素到带有神经网络的Policy Gradient。我们将所有这些放入130行Python中。（要点链接）让我们看看这是如何完成的。

上图：乒乓球。 下图：作为Markov决策过程（MDP）特例的乒乓演示：图形的每个顶点对应于游戏的某个状态，并且边线确定过渡到其他状态的概率。 每个肋骨也确定奖励。 目标是找到从任何州获得最大回报的最佳途径

打乒乓球是RL挑战的一个很好的例子。在ATARI 2600版本中，我们将自己打一个球拍。另一个球拍由内置算法控制。我们需要击球，以便其他球员没有时间击球。希望没有必要解释什么是乒乓球。在较低的级别上，游戏的工作方式如下：我们得到一个图像帧-字节数组210x160x3，并决定是否要向上或向下移动球拍。也就是说，我们只有两种选择来管理游戏。每次选择后，游戏模拟器都会执行动作并给予我们奖励：如果球超过了对手的球拍，则+1奖励；如果我们错过球，则为-1。否则为0。当然，我们的目标是移动球拍，以使我们获得尽可能多的回报。

在考虑解决方案时，请记住，我们将对乒乓做出很少的假设，因为它在实践中并不是特别重要。在大型任务中，例如操纵机器人，组装和导航，我们要考虑更多的事情。 Pong只是一个有趣的玩具测试用例，我们在玩这个游戏的过程中发现了如何编写非常通用的AI系统，该系统一天可以执行任意有用的任务。

神经网络作为RL策略 。首先，我们将确定我们的参与者（或“代理商”）执行的所谓政策。（（*）“代理商”，“环境”和“代理商政策”是RL理论的标准术语）。在我们的案例中，策略功能是神经网络。她将在入口处接受游戏的状态，然后在出口处决定要做什么-上下移动。作为我们最喜欢的简单计算模块，我们将使用两层神经网络，该网络将获取原始图像像素（总计100,800个数字（210 * 160 * 3）），并生成一个数字，指示将球拍向上移动的可能性。请注意，随机策略的使用是标准的，这意味着我们仅产生向上运动的概率。为了获得实际的移动，我们将使用此概率。当我们谈论培训时，其原因将变得更加清楚。

我们的政策功能包括2层全连接神经网络

更具体地说，假设在输入处得到一个向量X，它包含一组预处理像素。然后我们必须使用python \ numpy计算：

h = np.dot(W1, x) # compute hidden layer neuron activations h[h<0] = 0 # ReLU nonlinearity: threshold at zero logp = np.dot(W2, h) # compute log probability of going up p = 1.0 / (1.0 + np.exp(-logp)) # sigmoid function (gives probability of going up)

在此片段中，W1和W2是我们随机初始化的两个矩阵。我们不使用偏见，因为我们想要。请注意，最后我们使用了S形的非线性，这将输出概率降低到[0,1]范围。直观地讲，隐藏层中的神经元（权重位于W1中）可以检测各种游戏场景（例如，球在顶部，而我们的球拍在中间），然后W2中的权重可以决定在每种情况下我们是否应该上升或下降。当然，最初的随机W1和W2首先会在我们的神经播放器中引起痉挛和抽搐，这使他在飞机的控制上等同于自闭症。因此，现在唯一的任务就是找到W1和W2，从而开发出出色的游戏！

关于像素预处理的一句话-理想情况下，您需要将至少2帧传输到神经网络，以便它可以检测运动。但是为了简化这种情况，我们将应用两个帧的差。也就是说，我们将减去当前帧和前一帧，然后将差值应用于神经网络的输入。

听起来好像是不可能的事情。 在这一点上，我希望您了解RL问题的复杂性。我们得到100800个数字（210x160x 3），并将其发送到我们的神经网络，该神经网络将实施玩家的政策（顺便说一下，在矩阵W1和W2中轻松包含了大约一百万个参数）。假设我们在某个时候决定上升。游戏模拟器可以回答，这次我们将获得0个奖励，并为下一帧再提供100 800个数字。在获得非零奖励之前，我们可以重复此过程数百次！例如，假设我们最终获得了+1奖励。这太好了，但是我们怎么能说-是什么导致的呢？这是我们刚才所做的动作吗？还是后退76帧？或者，也许这首先与第10帧相关联，然后我们在第90帧做了正确的事情？以及我们如何找出-数以百万计的“笔”中的哪一个可以扭曲，以便在将来获得更大的成功？我们称此为确定某些动作的置信系数的任务。在乒乓球的特定情况下，我们知道如果球超过了对手，我们将得到+1。真正的原因是我们无意中将球沿着良好的路线踢了几帧，而随后执行的每个动作都丝毫不影响它。换句话说，我们面临着一个非常复杂的计算问题，并且一切看起来都令人沮丧。

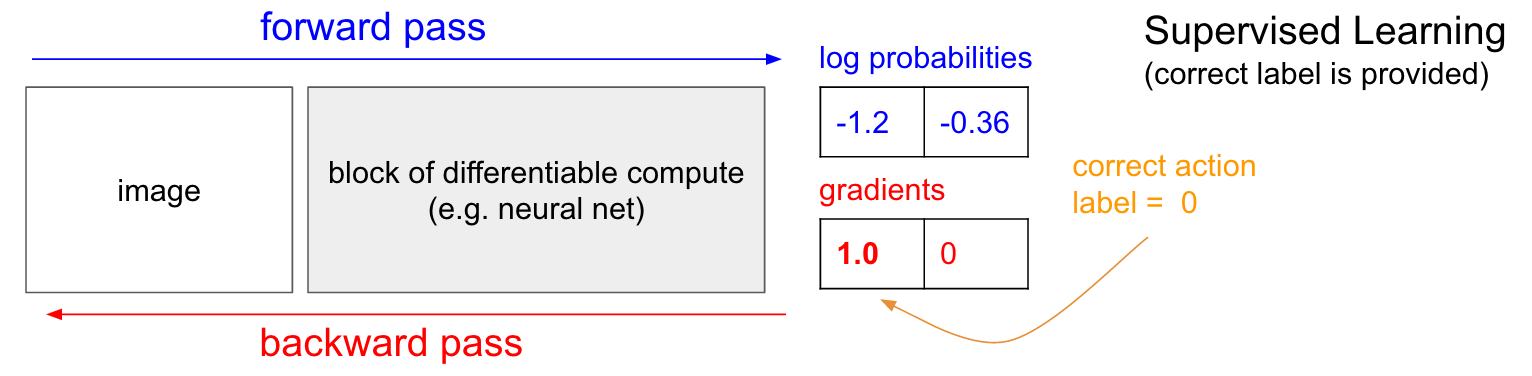
与老师一起训练。 在深入探讨政治梯度之前，我想简要回顾一下与老师一起进行教学的原因，因为正如我们将看到的那样，RL非常相似。请参考下表。在与老师的常规教学中，我们将图像传输到网络，并在输出中接收有关课程的一些数字概率。例如，在我们的案例中，我们有两个类：UP和DOWN。我使用对数概率（-1.2，-0.36）而不是30％和70％格式的概率，因为我们优化了正确类别（或标签）的对数概率。因为对数是单调的，所以这使数学计算更加优雅，并且等效于优化概率。

与老师一起训练时，我们将立即获得正确的课程（标签）。在训练阶段，尽管神经网络可能会有所不同，但是他们会确切地告诉我们现在需要采取什么正确的步骤（假设它是UP，标号0）。因此，我们计算梯度

（ ）

$\ nabla_ {W} \ log p（y = UP \ mid x）$ 调整网络设置。该梯度仅告诉我们如何更改数百万个参数中的每个参数，以使网络在相同情况下更有可能预测UP。例如，网络中的一百万个参数之一可以具有-2.1的梯度，这意味着如果我们将此参数增加一个小的正值（例如0.001），则UP的对数概率将减少2.1 * 0.001。（由于负号而减少）。如果我们应用渐变，然后使用反向传播算法更新参数，那么是的，当我们的网络将来看到相同或非常相似的图像时，将给出较高的UP概率。

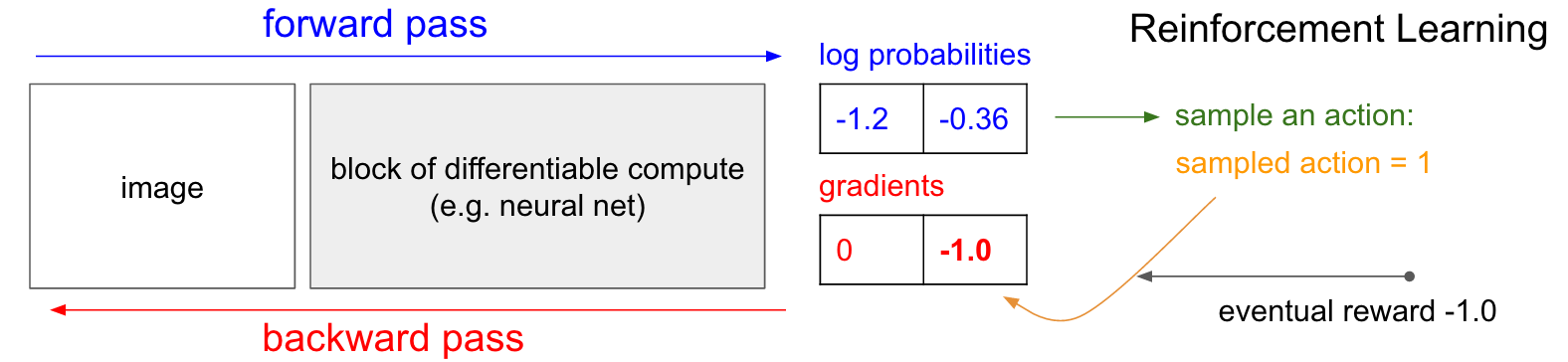
政治学的梯度（PG） 。是的，但是如果我们没有正确的强化训练标签，我们该怎么办？这是PG的解决方案（请再次参考下图）。我们的神经网络计算出上升30％（logprob -1.2）和下降7％（logprob -0.36）的概率。现在，我们从此分布中进行选择，并指定要执行的操作。例如，他们选择DOWN，然后将此动作发送到游戏模拟器。此时，请注意一个有趣的事实：我们可以像在与老师一起教课时那样立即计算并应用DOWN动作的坡度，从而使网络将来更有可能执行DOWN动作。因此，我们可以立即欣赏并记住该梯度。但是问题是，目前我们还不知道-下降是否很好？ 但是最有趣的是，我们可以稍等片刻，然后再应用渐变！ 在Pong中，我们可以等到游戏结束，然后获取我们获得的奖励（如果我们赢了，则为+1，如果我们输了，则为-1），然后将其输入作为渐变的因数。因此，如果我们为DOWN概率引入-1并进行反向传播，我们将重建网络参数，以便将来在遇到相同图像时执行DOWN动作的可能性较小，因为采用此动作会使我们输掉比赛。也就是说，我们将需要以某种方式记住游戏的一个情节中的所有动作（神经网络的输入和输出），并基于此阵列，以与老师教学几乎相同的方式扭曲神经网络。

这就是所需要的：我们有一个随机的政策来选择行动，然后在将来，鼓励最终导致良好结果的行动，而不鼓励导致不良结果的行动。此外，如果我们最终赢得比赛，奖励甚至不应为+1或-1。它可以是具有相同含义的任意值。例如，如果一切顺利，则奖励可能是10.0，然后我们将其用作渐变以开始反向传播反向传播。这就是神经网络的美。使用它们似乎是一个骗局：您可以在1万亿次运算中内置100万个参数，并且可以使程序学习使用随机梯度下降（SGD）进行任意操作。它不应该起作用，但是有趣的是我们生活在一个可以起作用的宇宙中。

如果我们玩简单的棋盘游戏，例如跳棋，那么顺序将大致相同。与minimax或alpha-beta裁剪算法有明显区别。在这些算法中，程序将向前迈出几步，了解游戏规则，并分析数百万个位置。在RL方法中，仅分析实际执行的动作。同时，神经网络并不期待，因为它对游戏规则一无所知。

锻炼顺序详细。 我们用W1，W2创建和初始化一个神经网络，并玩100局傍晚游戏（我们称其为“政治，政策出台的“磨合”）。假设每个游戏包含200帧，那么我们总共做出100 * 200 = 20,000个决定上升或下降。对于每种解决方案，我们都知道一个梯度，该梯度告诉我们在将来要在这种状态下鼓励或禁止该解决方案时应如何更改参数。现在剩下的就是标记我们做出的每个决定是好是坏。例如，假设我们赢了12场比赛而输了88场。我们将对获胜游戏做出的所有200 * 12 = 2400个决定，并做出积极的更新（为每个动作填充+1.0渐变，执行反向传播并更新参数鼓励我们在所有这些情况下选择的行动）。然后，我们将在输掉比赛中做出其他200 * 88 = 17,600个决定，并做出负面更新（不批准我们所做的事情）。这就是全部。现在，网络将更有可能重复已执行的操作，而不太可能重复未执行的操作。现在，我们通过略有改进的新策略又玩了100场游戏，然后重复应用渐变。

4个游戏的卡通方案。 每个黑色圆圈都是一种游戏状态（下面显示了三个状态示例），每个箭头都是标有所选动作的过渡。 在这种情况下，我们赢了2场，输了2场。 我们参加了赢得的两场比赛，并轻轻鼓励了我们在本集中所做的所有动作。 相反，我们还将进行两场输掉的比赛，并稍微劝阻我们在本集中所做的每个动作。

如果您对此进行反思，您将开始发现一些有趣的属性。例如，如果我们在第50帧进行了良好的动作，正确踢球，但随后在第150帧错过了球怎么办？由于我们输掉了比赛，因此每个动作现在都标记为不良，这是否会妨碍正确击中第50帧？您说的没错-这个派对就是这样。但是，当您考虑成千上万的游戏过程时，正确执行篮板球将增加您将来获胜的可能性。平均而言，对于适当的球拍打击，您会看到比消极更新要多的积极信息。而且神经网络的实施策略最终将产生正确的反应。

更新：2016年12月9日是另一种视图。在上面的解释中，我使用了诸如“定义梯度和反向传播”的术语，这是一项非常熟练的技术。如果您习惯于编写自己的反向传播反向传播代码或使用Torch，则可以完全控制渐变。但是，如果您习惯使用Theano或TensorFlow，您会有些困惑，因为backprop代码是完全自动化的并且很难自定义。在这种情况下，以下替代视图可能会更有成效。与老师一起教学时，通常的目标是最大程度地提高

（ ）

$\ sum_i \ log p（y_i \ mid x_i）$ 在哪里

，

$x_i，y_i$ -训练示例（例如图像及其标签）。将梯度应用于策略功能与教师培训完全吻合，但有两个小区别：1）我们没有正确的标签

$y_i$ ，因此，作为“假标签”，我们使用收到的操作来从策略中选择

$x_i$ ，以及2）我们为每个动作引入另一个权宜性系数（优势）。因此，最终，我们的损失现在看起来像

（ ）

$\ sum_i A_i \ log p（y_i \ mid x_i）$ 在哪里

$y_i$ -这是我们对样本执行的操作，并且

$A_i$ 是数字，我们称为权宜系数。例如，对于乒乓球，该值

$A_i$ 如果我们最终赢得该集，则可能是1.0；如果我们输了，则可能是-1.0。这样可以确保我们最大程度地记录导致良好结果的动作的可能性，并最大程度地减少未记录结果的可能性。由于许多呼吁而采取的中立行动不会特别影响政治功能。因此，强化学习与与老师的学习完全相同，但是在不断变化的数据集（情节）上，还有其他因素。

更先进的可行性功能。 我还承诺会提供更多信息。到目前为止，我们已经根据我们是否获胜来评估每个动作的正确性。在更一般的RL设置中，我们将获得“有条件的奖励”

$r_t$ 对于每个步骤，取决于步骤编号或时间。一种常见的选择是使用折现系数，因此上图中的“可能的报酬”为

$R_t = \ sum_ {k = 0} ^ {\ infty} \ gamma ^ k r_ {t + k}$ 在哪里

$\伽玛$ 是从0到1的数字，称为折扣系数（例如0.99）。该表述表示，我们鼓励采取行动的力量是所有奖励的加权总和，但随后的奖励却没有那么重要。就是说，更好地鼓励采取行动的短链，而采取行动的长链的尾巴则变得不那么重要。实际上，您还需要将它们标准化。例如，假设我们计算

$R_t$ 适用于一系列100个游戏情节中的所有20,000个动作。一个很好的主意是在将它们连接到反向传播算法之前，将它们标准化（减去平均值，除以标准差）。因此，我们总是鼓励和劝阻大约一半的行动。这样可以减少波动并使政策更加趋同。在[ 链接 ]可以找到更深入的研究。

从策略功能派生。 我还想简要描述一下数学上如何采用渐变。政治功能的梯度是更一般性理论的特例。一般情况是，当我们有以下形式的表达式时

$E_ {x \ sim p（x \ mid \ theta）} [f（x）]$ ，即某些标量函数的期望

$f（x）$ 及其参数的一些分布

$p（x; \ theta）$ 由某些向量参数化

$\ theta$ 。然后

$f（x）$ 将成为我们的奖励函数（或更一般意义上的权宜函数），以及离散分布

$p（x）$ 将是我们的政策，实际上具有以下形式

$p（一个\中旬我）$ 给出图片的动作概率

$我$ 。然后我们对如何通过其参数移动p的分布感兴趣

$\ theta$ 放大

$f$ （即，我们如何更改网络设置，以使操作获得更高的回报）。我们有这个：

$\开始{align} \ nabla _ {\ theta} E_x [f（x）]＆= \ nabla _ {\ theta} \ sum_x p（x）f（x）＆\ text {期望的定义} \\＆= \ sum_x \ nabla _ {\ theta} p（x）f（x）和\文字{交换总和和渐变} \\＆= \ sum_x p（x）\ frac {\ nabla _ {\ theta} p（x）} {p （x）} f（x）＆\文字{乘以并除以} p（x）\\＆= \ sum_x p（x）\ nabla _ {\ theta} \ log p（x）f（x）＆\文字{使用以下事实：\ nabla _ {\ theta} \ log（z）= \ frac {1} {z} \ nabla _ {\ theta} z \\＆= E_x [f（x）\ nabla _ {\ theta} \ log p（x）]和\文本{期望的定义} \结束{align}$

我将尽力解释这一点。我们有一些分配

$p（x; \ theta）$ （我用了缩写

$p（x）$ 从中我们可以选择特定的值。例如，它可以是随机数发生器从中采样的高斯分布。对于每个示例，我们还可以计算估计函数

$f$ ，根据当前示例，它为我们提供了一些标量估计。所得方程式告诉我们如何通过其参数移动分布

$\ theta$ 如果我们想进一步根据它采取行动的例子来获得更高的利率

$f$ 。我们举一些行动的例子

$x$ 及其评估

$f（x）$ ，对于每个x，我们还评估第二项

$\ nabla _ {\ theta} \ log p（x; \ theta）$ 。这个乘数是多少？这就是向量-梯度，它为我们提供了参数空间中的方向，这将导致特定动作的可能性增加

$x$ 。换句话说，如果我们将θ推向

$\ nabla _ {\ theta} \ log p（x; \ theta）$ ，我们将看到此操作的新可能性会略有增加。如果回头看公式，它告诉我们应该朝这个方向乘以标量值

$f（x）$ 。这样可以确保评分较高（在本例中为奖励）的操作示例比指标较低的示例更“吸引”，因此，如果我们要根据

$p$ ，则概率密度将向更高的最终游戏点方向移动，这增加了获得具有高奖励的动作示例的可能性。重要的是不要从函数中获取梯度

$f$ ，因为它通常是无法区分且不可预测的。一

$p$ 可区分的

$\ theta$ 。那是

$p$ 是连续可调的离散分布，您可以在其中调整单个动作的概率。我们还假设

$p$ 标准化。

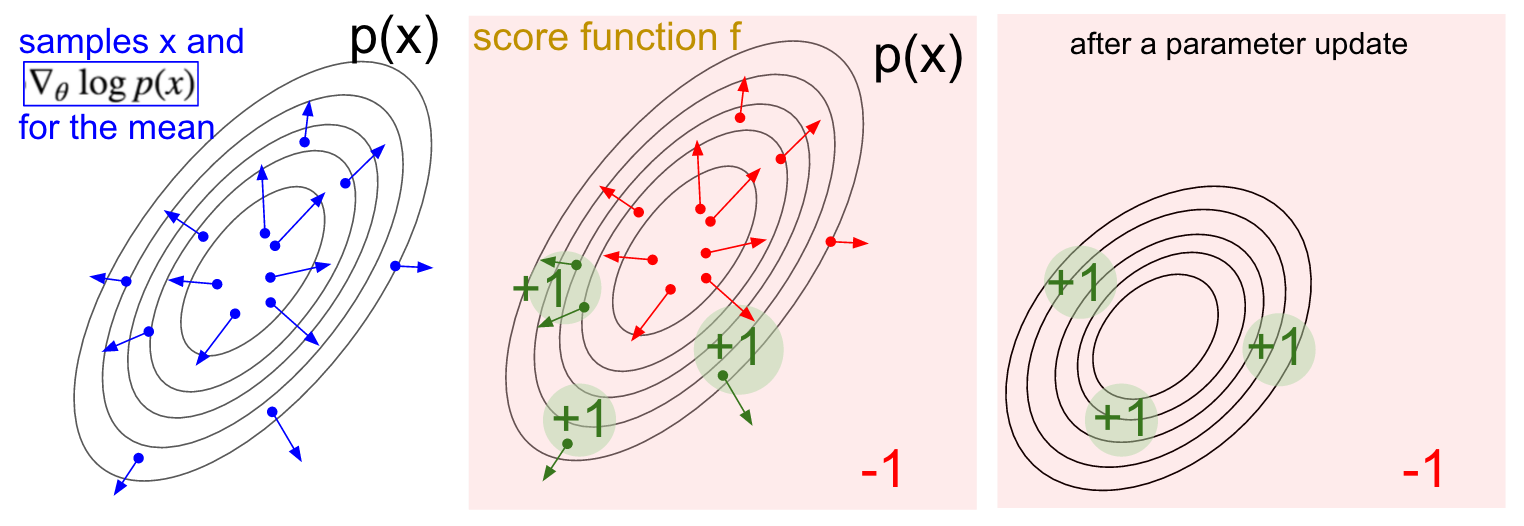渐变可视化。 左：高斯分布及其中的几个示例（蓝点）。 在每个蓝点处，我们还绘制了对数概率相对于平均参数的梯度。 箭头指示平均分布值应移动的方向，以增加此示例操作的可能性。 中间：添加了一些求值函数，除某些小区域中的+1之外，其他所有地方都提供-1（请注意，这可以是任意的，不一定是可微分的标量函数）。 箭头现在采用了颜色编码，因为由于乘法运算，我们将平均所有绿色箭头的正值和负红色箭头的值。 右：更新参数后，绿色箭头和反向红色箭头将我们向左和向下推。 如果需要，此分布中的样本现在将具有更高的预期评级。

我希望与RL的联系清楚。我们的政策为我们提供了一些行动示例，其中一些行动比其他行动更好（根据权宜功能判断）。更改策略设置的方法是运行，采用所选操作的梯度，将其乘以等级并添加我们在上方所做的所有操作。对于更彻底的结论，我建议约翰·舒尔曼
（John Shulman）进行一次演讲。
培训。好吧，我们已经制定了政治职能梯度的原则。我用130行Python脚本实现了整个方法，该脚本使用了OpenAI Gym提供的现成的ATAI 2600 Pong仿真器。我使用RMSProp算法训练了一个包含200个隐层神经元的两层神经网络，进行了10次发作（根据规则，每个发作包括几次抽签，该发作持续得分21）。我并没有设置过多的超级参数并在慢速的Macbook上进行了实验，但是经过三天的锻炼，我得到了一个比内置播放器更好玩的策略。总的情节总数约为8,000，因此该算法玩了大约200,000傍游戏，这相当多，总共产生了约800次权重更新。如果我使用ConvNets在GPU上进行训练，那么几天之内，我就能取得不错的成绩；如果我优化超参数，那么我总能赢。但是，我并没有花费太多时间进行计算或设置，所以取而代之的是Pong AI，它说明了主要思想并且效果很好：

.

.我们还可以查看获得的神经网络权重。由于进行了预处理，我们的每个输入都是80x80的差异图像（当前帧减去前一帧）。来自层W1的每个神经元都连接到由200个神经元组成的隐藏层W2。债券数量为80 * 80 * 200。让我们尝试分析这些连接。我们将对W2层的所有神经元进行分类，并可视化导致它的权重。根据从W1神经元到一个W2神经元的尺度，我们将制作80x80图片。下面是40张这样的W2图片（总共200张）。白色像素为正权重，黑色像素为负。请注意，几个W2神经元被调谐到以虚线编码的飞行球。在游戏中，球只能在一个地方，因此，这些神经元具有多种用途，如果球在这些线的某处，它们将“射击”。黑白交替很有趣，因为当球沿着轨道移动时，神经元的活动会像正弦波一样波动。由于ReLU的缘故，他只会在某些位置“射击”。图像中有很多噪点，如果我使用L2正则化，则噪点会更少。

什么都没发生。因此，我们学习了如何使用策略功能的梯度在图片上打乒乓球，并且效果很好。这种方法是一种奇怪的“建议和验证”形式，其中“猜测”是指在游戏的多个情节中执行我们的政策，而“检查”则鼓励采取行动以产生良好的结果。一般而言，这代表了我们当前如何处理强化学习问题的当前水平。如果您直观地理解算法并知道其工作原理，那么您至少应该会有些失望。特别是什么时候不起作用？

将此与人可以学习打乒乓球的方式进行比较。您自己给他们看比赛，然后说：“您控制球拍，您可以上下移动球拍，您的任务是将球扔到内置程序控制的另一位球员身上，”您就可以出发了。请注意一些区别：

- , , , . RL , . , ( ), , . . , , , , , , , , .
, ( , , , ..), ( «» « , , , - - . .). «» / . , , ( ) ( , ).
— (brute force), , . . , , , . , «» , . , , .
, , . , , . .

: : RL. , , . , . , 99% . , «» . : «», , - , - , - , , . « , ».

我还要强调一个事实，相反，在许多游戏中，政治梯度很容易击败一个人。特别是，这适用于具有频繁奖励的游戏，这些游戏需要准确，快速的反应并且没有长期计划。 PG方法很容易看出奖励和行动之间的短期关联。您可以在我们的代理商Pong中看到类似的内容。当他只等球时，他就制定了策略，然后迅速移动以仅在最边缘抓住球，这就是为什么球以很高的垂直速度弹跳的原因。特工连续重复数次获胜，重复了这种简单的策略。在许多游戏（弹球游戏，突破游戏）中，深度Q学习通过简单而精确的动作将一个人吸引并践踏到泥泞中。

一旦了解了这些算法的“技巧”，就可以了解它们的优缺点。特别是，这些算法在构建人们可以用来快速学习的游戏的抽象概念方面远远落后于人们。一旦计算机查看了像素阵列并注意到了钥匙，就进了门，然后自以为是，拿钥匙去门就好了。目前尚无与此相关的东西，而试图到达那里是一个活跃的研究领域。

神经网络中的不可微计算。我想提到非博弈策略梯度的另一个有趣应用：它允许我们使用与不可微计算执行（或交互）的组件来设计和训练神经网络。这个想法由Williams于1992年首次提出。并且最近在循环视觉注意力模型中得到了普及。在处理具有一系列中心凹低分辨率外观的图像的模型的背景下，这种模式称为“密切关注”，类似于我们的眼睛如何以运行中的中央视觉检查对象。在每次迭代中，RNN将接收一小幅图像片段，并选择需要进一步查看的位置。例如，RNN可以查看位置（5.30），获取图像的小片段，然后决定查看（24，50），依此类推。神经网络的一部分选择了要进一步查看的位置，然后对其进行检查。不幸的是，该操作不可区分，因为我们不知道如果在其他地方进行采样会发生什么。在更一般的情况下，请考虑具有多个输入和输出的神经网络：

请注意，大多数蓝色箭头与往常一样是可区分的，但是某些视图转换可能还包括未区分的选择操作，该操作以红色突出显示。我们可以沿相反的方向穿过蓝色箭头，但是红色箭头是一种依赖关系，通过它我们无法反向传播反向传播。

梯度政策要抢救！让我们考虑执行采样的网络部分，它可以表示为嵌入在大型神经网络中的随机策略的函数。因此，在训练过程中，我们将提供几个示例（由下面的分支指示），然后我们将鼓励最终产生良好结果的样本（在这种情况下，例如，以最后的损失来衡量）。换句话说，我们将像往常一样使用反向传播器训练蓝色箭头中包含的参数，但现在红色箭头中包含的参数将使用策略梯度独立于后向传递进行更新，从而鼓励降低样本损失。最近也很好地构想了这个想法。使用随机计算图进行梯度估计。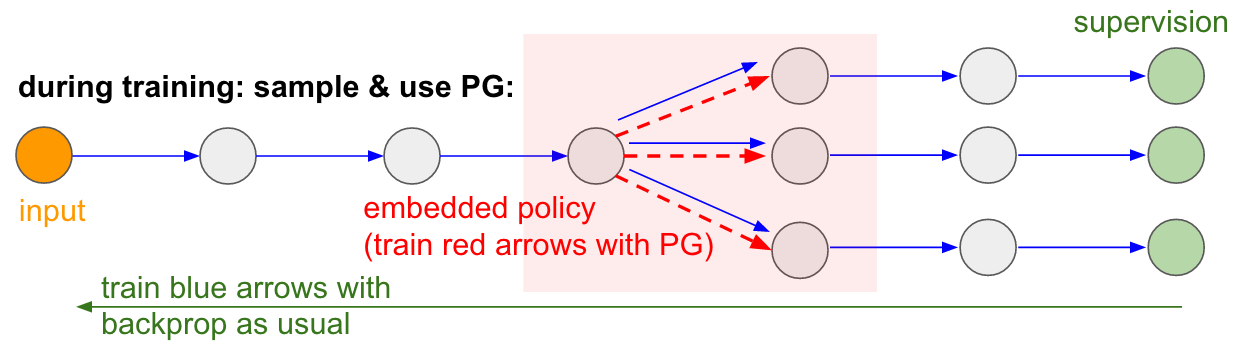

经过训练的输入/输出在随机存取存储器中。您还将在其他许多文章中找到这种想法。例如，神经图灵机有一个存储带，他们可以用它们来读写。要执行写操作，您需要执行类似m [i] = x的操作，其中i和x由RNN神经网络预测。但是，没有信号告诉我们如果我们写j，损失函数会发生什么！ =I。因此，NTM可以执行软读取和写入操作。他预测注意力分布函数a，然后对所有i执行：m [i] = a [i] * x。现在是可区分的，但是我们必须付出高昂的计算成本，对所有单元格进行排序。

但是，我们可以使用策略梯度从理论上解决此问题，就像RL-NTM一样。我们仍然可以预测注意力a的分布，但不是穷举搜索，而是随机选择写作地点：i =样本（a）； m [i] = x。在训练期间，我们可以针对一小部分i进行此操作，最后找到一个比其他i更好用的集合。一个巨大的计算优势是，在测试期间，您可以从一个单元读取/写入。但是，如文档中所述，该策略很难实现，因为您需要经历许多选择，并且几乎偶然地使用了有效的算法。目前，研究人员一致认为，只有在有多个离散选项且您不需要梳理庞大的搜索空间时，PG才能很好地工作。

但是，借助策略梯度，并且在有大量数据和计算能力的情况下，原则上我们可以梦想很多。例如，我们可以设计学习与大型不可微对象（例如Latex编译器）进行交互的神经网络。例如，为了让char-rnn生成现成的Latex代码，SLAM系统，LQR求解器或其他东西。或者，例如，超级智能可能想要学习如何通过TCP / IP（也是不可区分的）与Internet进行交互，以访问捕获世界所需的信息。这是一个很好的例子。

结论

我们看到策略梯度是一种功能强大的通用算法，例如，我们从130条Python行中的原始像素中训练了ATARI Pong代理。通常，可以使用相同的算法来训练任意游戏的代理，并且希望有一天我们可以使用它来解决现实世界中的控制问题。最后，我想补充一些评论：

关于AI的发展。我们看到该算法通过暴力搜索起作用，在这种情况下，您首先会随机犹豫，并且必须在策略功能更改其参数之前至少一次（理想情况下是偶然）偶然发现有用的情况。我们还看到，一个人以完全不同的方式来解决这些问题，类似于快速构建抽象模型。由于很难抽象地想象这些抽象模型（如果不是不可能的话），这也是最近对生成模型和软件归纳产生了极大兴趣的原因。

关于机器人技术的使用。该算法不适用于难以获得大量研究的情况。例如，您可以让一个（或几个）机器人与世界实时互动。对于该算法的简单应用而言，这还不够。确定性的政策梯度是旨在减轻这一问题的工作领域之一。这种方法不是进行实际尝试，而是从对评估函数建模的第二个神经网络（称为评论家）获取梯度信息。从原则上讲，这种方法对于高维度的行为可能是有效的，因为在这种情况下，随机抽样的覆盖率很低。另一种相关方法是扩大我们在Google机器人农场中开始看到的机器人技术甚至是带有自动驾驶仪的Tesla S +。

还有一条工作线试图通过添加其他控件来减少搜索过程的希望。例如，在许多实际情况下，您可以直接从人那里获得最初的发展方向。例如，AlphaGo首先使用老师的培训来预测人类的行为（例如远程机器人控制，学徒制，轨迹优化，完整策略搜索）。然后使用PG配置最终的策略，以实现真正的目标-赢得比赛。

在某些情况下，可能会有更少的预设（例如，用于远程控制机器人），并且存在使用该实习前数据的方法。最后，如果人们不提供特定的数据或设置，则在某些情况下也可以通过使用非常昂贵的优化方法进行计算来获得它们，例如，通过在已知动态模型（例如物理模拟器中的F = ma）中优化轨迹来进行计算，或者在某些情况下创建近似的本地模型时（如在用于托管策略搜索的非常有前途的结构中看到的那样）。

关于在实践中使用PG。我想更多地谈论RNN。我认为RNN似乎很神奇，可以自动解决与任意序列有关的问题。事实是，使这些模型正常工作可能很棘手。需要护理和经验，以及何时知道更简单的方法可以帮助您90％。政策梯度也是如此。它们不会像那样自动运行：您需要有很多示例，它们可以永久地训练，当它们不起作用时很难调试。在到达火箭筒之前，您应该始终尝试从小手枪射击。例如，在加强训练的情况下，应始终首先检查交叉熵方法（CEM）。，一种受进化启发的简单的随机“猜测和检验”方法。而且，如果您坚持尝试执行任务的策略梯度，请确保您知道具体的窍门。从简单开始，并使用一个称为TRPO的PG选项，该选项几乎总是比传统PG更好，更一致。基本思想是避免由于使用新旧政策之间的Kulbak-Leibler距离而更新太多更改您的政策的设置。

仅此而已！希望我给您一个关于强化学习的概念，有什么问题，如果您想帮助推广RL，我邀请您在我们的OpenAI Gym中进行：）下次见！

人工智能和自动驾驶特斯拉研究人员，开发人员，总监Andrej Karpathy，

其他信息：

2018年手指深度学习课程
https://habr.com/en/post/414165/ 手指深度学习

开放课程2019
https：// // habr.com/ru/company/ods/blog/438940/

NSU物理学院
http://www.phys.nsu.ru/

强化深度学习：原始像素乒乓球

结论

More articles: