🎱 👩🏿‍🍳 👦🏽 朱莉娅和坐标下降法 🖖🏼 🧒🏻 🛷

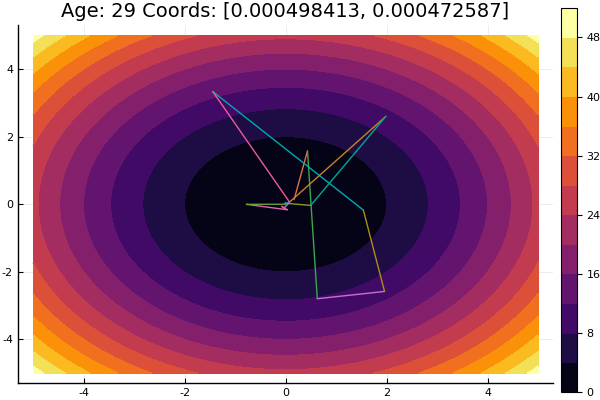
坐标下降法是多维优化的最简单方法之一，并且在找到具有相对平滑地形的函数的局部最小值方面做得很好，因此最好从中开始熟悉优化方法。

极值的搜索是在坐标轴的方向上进行的，即在搜索过程中，仅更改一个坐标。因此，多维问题简化为一维问题。

演算法

第一周期：

$x_1 = var$ ， $x_2 = x_2 ^ 0$ ， $x_3 = x_3 ^ 0$ ，...， $x_n = x_n ^ 0$ 。
寻找极值功能 $f（x_1）$ 。将函数的极点放在该点 $x_1 ^ 1$ 。
$x_1 = x_1 ^ 1$ ， $x_2 = var$ ， $x_3 = x_3 ^ 0$ ，...， $x_n = x_n ^ 0$ 。极值功能 $f（x_2）$ 等于 $x_2 ^ 1$
...
$x_1 = x_1 ^ 1$ ， $x_2 = x_2 ^ 1$ ， $x_3 = x_3 ^ 1$ ，...， $x_n = var$ 。
作为执行n个步骤的结果，发现了一个极端的新方法 $（x_1 ^ 1，x_2 ^ 1，...，x_n ^ 1）$ 。接下来，我们检查结束帐户的条件：如果满足条件，则找到解决方案，否则我们将执行一个以上的周期。

准备工作

检查软件包版本：

(v1.1) pkg> status Status `C:\Users\User\.julia\environments\v1.1\Project.toml` [336ed68f] CSV v0.4.3 [a93c6f00] DataFrames v0.17.1 [7073ff75] IJulia v1.16.0 [47be7bcc] ORCA v0.2.1 [58dd65bb] Plotly v0.2.0 [f0f68f2c] PlotlyJS v0.12.3 [91a5bcdd] Plots v0.23.0 [ce6b1742] RDatasets v0.6.1 [90137ffa] StaticArrays v0.10.2 [8bb1440f] DelimitedFiles [10745b16] Statistics

我们定义了一个用于绘制表面线或水平线的函数，通过该函数可以方便地调整图形的边界：

 using Plots plotly() #   function plotter(plot_fun; low, up) Xs = range(low[1], stop = up[1], length = 80) Ys = range(low[2], stop = up[2], length = 80) Zs = [ fun([xy]) for x in Xs, y in Ys ]; plot_fun(Xs, Ys, Zs) xaxis!( (low[1], up[1]), low[1]:(up[1]-low[1])/5:up[1] ) #   yaxis!( (low[2], up[2]), low[2]:(up[2]-low[2])/5:up[2] ) end

作为模型函数，我们选择椭圆抛物面

 parabol(x) = sum(u->u*u, x) fun = parabol plotter(surface, low = [-1 -1], up = [1 1])

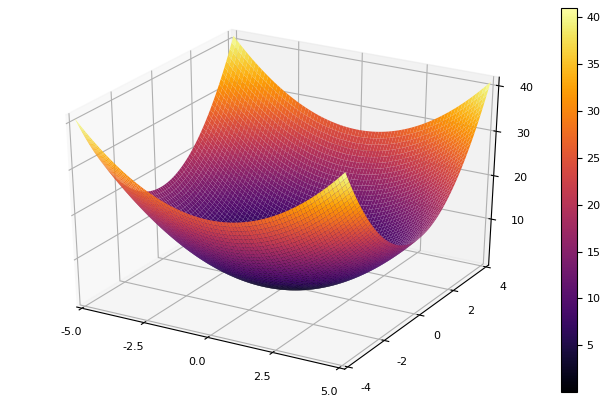
坐标下降

我们在一个函数中实现该方法，该函数采用一维优化方法的名称，问题的维数，期望的误差，初始近似值以及绘制水准线的限制。所有参数均设置为默认值。

 function ofDescent(odm; ndimes = 2, ε = 1e-4, fit = [.5 .5], low = [-1 -1], up = [1 1]) k = 1 #      sumx = 0 sumz = 1 plotter(contour, low = low, up = up) #    x = [ fit[1] ] #     y = [ fit[2] ] #      while abs(sumz - sumx) > ε && k<80 fitz = copy(fit) for i = 1:ndimes odm(i, fit, ε) #    end push!(x, fit[1]) push!(y, fit[2]) sumx = sum(abs, fit ) sumz = sum(abs, fitz) #println("$k $fit") k += 1 end #     scatter!(x', y', legend = false, marker=(10, 0.5, :orange) );# , ,  p = title!("Age = $(size(x,1)) f(x,y) = $(fun(fit))") end

接下来，我们将尝试各种一维优化方法。

牛顿法

（ ） （ ）

$x_ {n + 1} = x_n-\ frac {f（x_n）} {f'（x_n）}$

该方法的想法很简单，实现也很简单

 #  dfun = (x, i) -> i == 1 ? 2x[1] + x[2]*x[2] : 2x[2] + x[1]*x[1] function newton2(i, fit, ϵ) k = 1 oldfit = Inf while ( abs(fit[i] - oldfit) > ϵ && k<50 ) oldfit = fit[i] tryfit = fun(fit) / dfun(fit, i) fit[i] -= tryfit println(" $k $fit") k+=1 end end ofDescent(newton2, fit = [9.1 9.1], low = [-4 -4], up = [13 13])

牛顿对初始近似值有很高的要求，并且在不限制步长的情况下，他可以轻松地驶向未知的距离。计算导数是可取的，但是可以省去很小的变化。我们修改功能：

 function newton(i, fit, ϵ) k = 1 oldfit = Inf x = [] y = [] push!(x, fit[1]) push!(y, fit[2]) while ( abs(oldfit - fit[i]) > ϵ && k<50 ) fx = fun(fit) oldfit = fit[i] fit[i] += 0.01 dfx = fun(fit) fit[i] -= 0.01 tryfit = fx*0.01 / (dfx-fx) #        if( abs(tryfit) > abs(fit[i])*10 ) push!(x, fit[1]) push!(y, fit[2]) break end fit[i] -= tryfit #println(" $k $fit") push!(x, fit[1]) push!(y, fit[2]) k+=1 end #  - -   plot!(x, y, w = 3, legend = false, marker = :rect ) end ofDescent(newton, fit = [9.1 9.1], low = [-4 -4], up = [13 13])

反抛物线插值

一种不需要导数知识并具有良好收敛性的方法

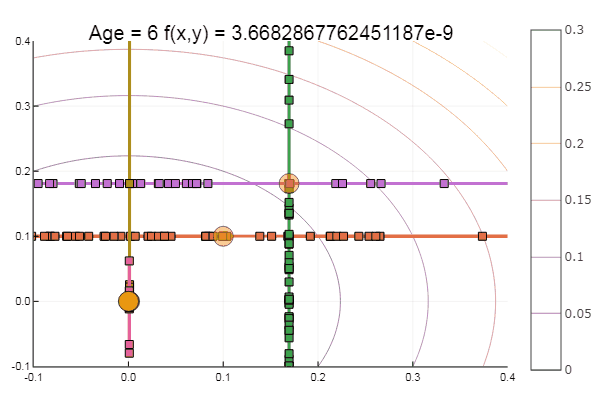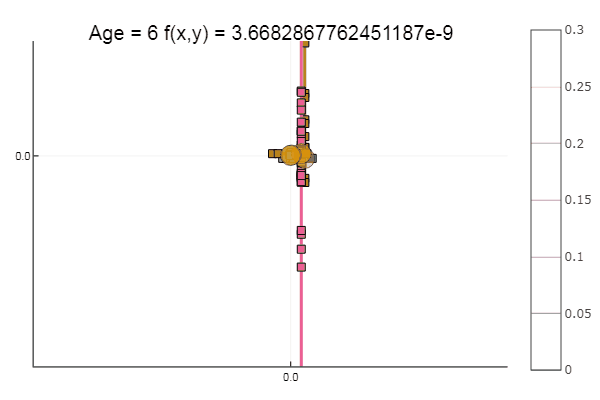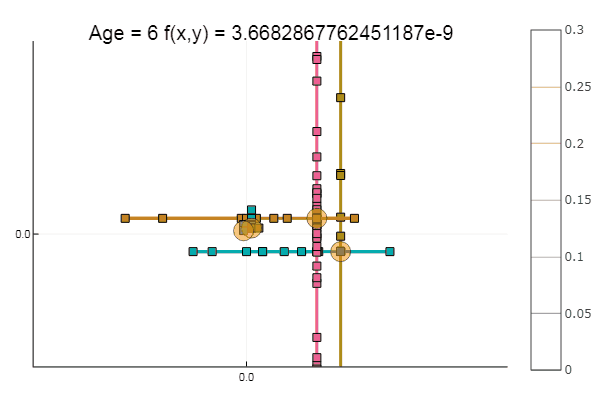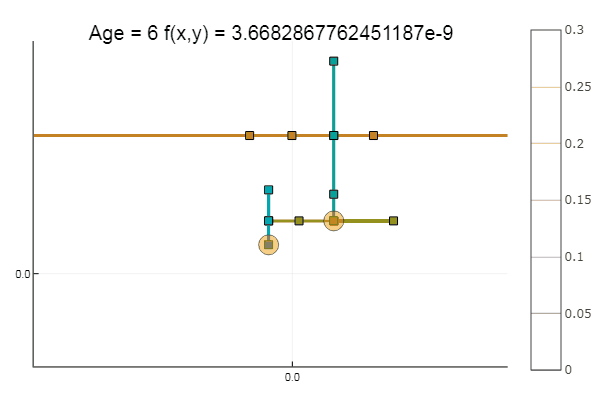
 function ipi(i, fit, ϵ) # inverse parabolic interpolation n = 0 xn2 = copy(fit) xn1 = copy(fit) xn = copy(fit) xnp = zeros( length(fit) ) xy = copy(fit) xn2[i] = fit[i] - 0.15 xn[i] = fit[i] + 0.15 fn2 = fun(xn2) fn1 = fun(xn1) while abs(xn[i] - xn1[i]) > ϵ && n<80 fn = fun(xn) a = fn1*fn / ( (fn2-fn1)*(fn2-fn ) ) b = fn2*fn / ( (fn1-fn2)*(fn1-fn ) ) c = fn2*fn1 / ( (fn -fn2)*(fn -fn1) ) xnp[i] = a*xn2[i] + b*xn1[i] + c*xn[i] xn2[i] = xn1[i] xn1[i] = xn[i] xn[i] = xnp[i] fn2 = fn1 fn1 = fn n += 1 println(" $n $xn $xn1") xy = [xy; xn] end fit[i] = xnp[i] plot!(xy[:,1], xy[:,2], w = 3, legend = false, marker = :rect ) end ofDescent(ipi, fit = [0.1 0.1], low = [-.1 -.1], up = [.4 .4])

如果我们使初始近似值更糟，则对于每个坐标下降时代，该方法将开始需要大量步骤。在这方面，他的兄弟获胜

顺序抛物线插值

它还需要三个起点，但是在许多测试功能上，它显示出更令人满意的结果。

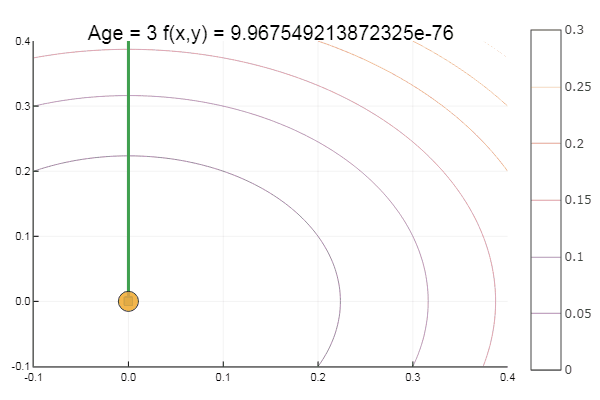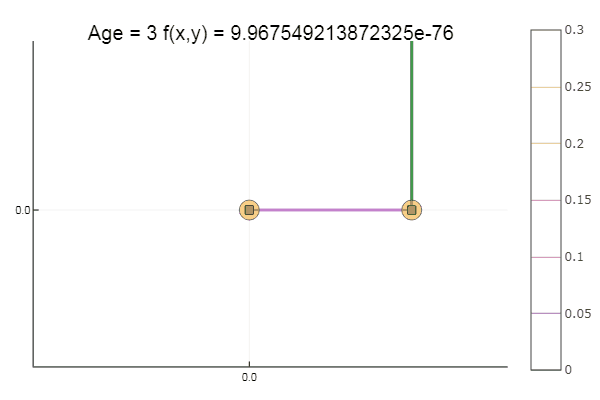
 function spi(i, fit, ϵ) # sequential parabolic interpolation n = 0 xn2 = copy(fit) xn1 = copy(fit) xn = copy(fit) xnp = zeros( length(fit) ) xy = copy(fit) xn2[i] = fit[i] - 0.01 xn[i] = fit[i] + 0.01 fn2 = fun(xn2) fn1 = fun(xn1) while abs(xn[i] - xn1[i]) > ϵ && n<200 fn = fun(xn) v0 = xn1[i] - xn2[i] v1 = xn[i] - xn2[i] v2 = xn[i] - xn1[i] s0 = xn1[i]*xn1[i] - xn2[i]*xn2[i] s1 = xn[i] *xn[i] - xn2[i]*xn2[i] s2 = xn[i] *xn[i] - xn1[i]*xn1[i] xnp[i] = 0.5(fn2*s2 - fn1*s1 + fn*s0) / (fn2*v2 - fn1*v1 + fn*v0) xn2[i] = xn1[i] xn1[i] = xn[i] xn[i] = xnp[i] fn2 = fn1 fn1 = fn n += 1 println(" $n $xn $xn1") xy = [xy; xn] end fit[i] = xnp[i] plot!(xy[:,1], xy[:,2], w = 3, legend = false, marker = :rect ) end ofDescent(spi, fit = [16.1 16.1], low = [-.1 -.1], up = [.4 .4])

走出一个非常糟糕的起点需要三步！很好...但是所有方法都有一个缺点-它们收敛到局部最小值。现在让我们利用阿克莱的功能进行研究

（ ， ） 左 左 （ 右 ） 右 左 左 （ 右 ） 右

$f（x，y）=-20 \ exp \左[-0.2 {\ sqrt {0.5 \左（x ^ {2} + y ^ {2} \右）}} \右]-\ exp \左[ 0.5 \左（\ cos 2 \ pi x + \ cos 2 \ pi y \右）\右] + e + 20$

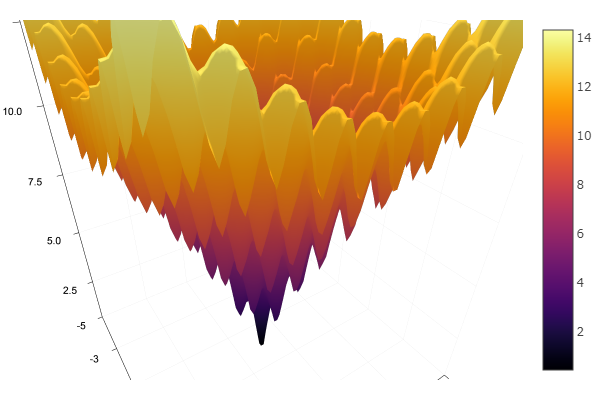
 ekly(x) = -20exp(-0.2sqrt(0.5(x[1]*x[1]+x[2]*x[2]))) - exp(0.5(cospi(2x[1])+cospi(2x[2]))) + 20 + ℯ # f(0,0) = 0, x_i ∈ [-5,5] fun = ekly plotter(surface, low = [-5 -5], up = [5 5])

 ofDescent(spi, fit = [1.4 1.4], low = [-.1 -.1], up = [2.4 2.4])

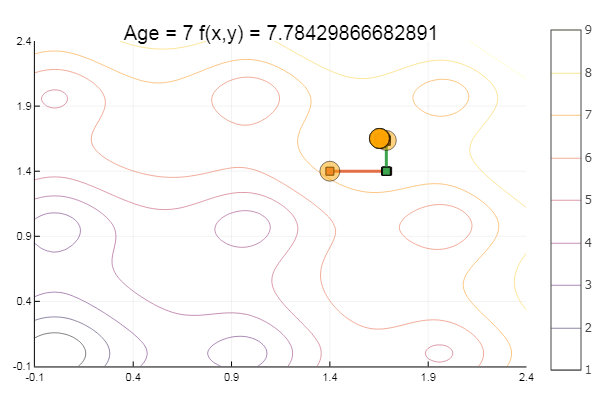
黄金分割法

理论尽管实现起来很复杂，但该方法有时会通过跳过局部最小值来很好地展示自己

 function interval(i, fit, st) d = 0. ab = zeros(2) fitc = copy(fit) ab[1] = fitc[i] Fa = fun(fitc) fitc[i] -= st Fdx = fun(fitc) fitc[i] += st if Fdx < Fa st = -st end fitc[i] += st ab[2] = fitc[i] Fb = fun(fitc) while Fb < Fa d = ab[1] ab[1] = ab[2] Fa = Fb fitc[i] += st ab[2] = fitc[i] Fb = fun(fitc) # println("----", Fb, " ", Fa) end if st < 0 c = ab[2] ab[2] = d d = c end ab[1] = d ab end function goldsection(i, fit, ϵ) ϕ = Base.MathConstants.golden ab = interval(i, fit, 0.01) α = ϕ*ab[1] + (1-ϕ)*ab[2] β = ϕ*ab[2] + (1-ϕ)*ab[1] fit[i] = α Fa = fun(fit) fit[i] = β Fb = fun(fit) while abs(ab[2] - ab[1]) > ϕ if Fa < Fb ab[2] = β β = α Fb = Fa α = ϕ*ab[1] + (1-ϕ)*ab[2] fit[i] = α Fa = fun(fit) else ab[1] = α α = β Fa = Fb β = ϕ*ab[2] + (1-ϕ)*ab[1] fit[i] = β Fb = fun(fit) end println(">>>", i, ab) plot!(ab, w = 1, legend = false, marker = :rect ) end fit[i] = 0.5(ab[1] + ab[2]) end ofDescent(goldsection, fit = [1.4 1.4], low = [-.1 -.1], up = [1. 1.])

坐标下降就可以了。所提供方法的算法非常简单，因此以您喜欢的语言实现它们并不困难。将来，您可以考虑使用Julia语言的内置工具，但是现在您想用手摸一摸，可以说，考虑更复杂，更高效的方法，然后可以进行全局优化，同时与另一种语言的实现进行比较。

文学作品

Zaitsev V.V.物理学家的数值方法。非线性方程式和优化：教程。 -萨马拉，2005年 -86岁
Ivanov A.V.优化光学系统的计算机方法。学习指南。 –SPb：SPbU ITMO，2010年-114s。
Popova T. M.多维优化方法：针对“应用数学” / comp方向的学生，在“优化方法”学科中实验室工作的指南和任务。 T. M. Popova。 -哈巴罗夫斯克：太平洋出版社。州大学，2012.-44羽

朱莉娅和坐标下降法

演算法