Geekly articles weekly

朱莉娅，梯度下降和单纯形法


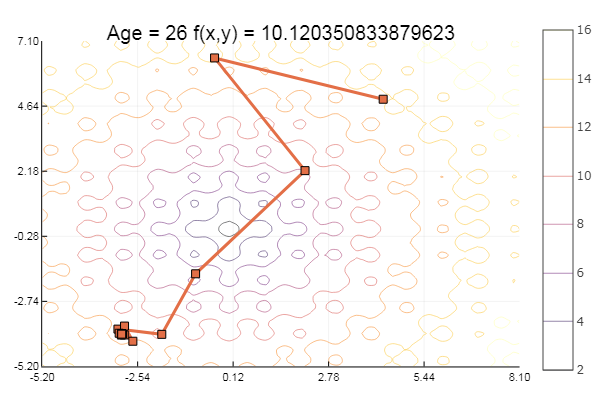
我们继续了解多维优化方法。


接下来，提出了通过执行速度分析的最快下降方法的实现，以及通过Julia和C ++语言实现的Nelder-Mead方法的实现。


梯度下降法


在梯度（最大值）或反梯度（最小值）的方向上逐步进行极值搜索。 在梯度方向（反梯度）的每个步骤中，都会进行移动，直到函数增加（减小）为止。


对于理论，请遵循以下链接：



使用模型功能，我们选择一个椭圆抛物面并设置渲染浮雕的功能：


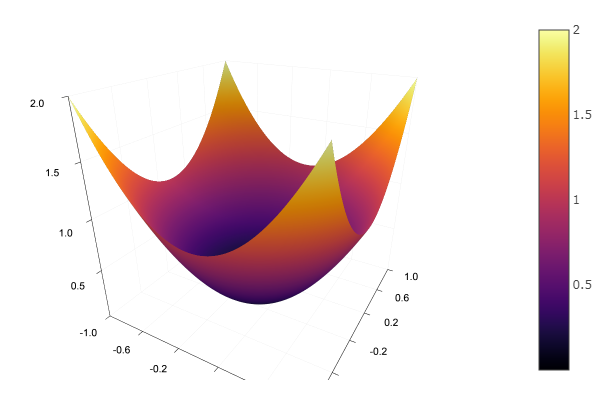
using Plots plotly() #   function plotter(plot_fun; low, up) Xs = range(low[1], stop = up[1], length = 80) Ys = range(low[2], stop = up[2], length = 80) Zs = [ fun([xy]) for x in Xs, y in Ys ]; plot_fun(Xs, Ys, Zs) xaxis!( (low[1], up[1]), low[1]:(up[1]-low[1])/5:up[1] ) #   yaxis!( (low[2], up[2]), low[2]:(up[2]-low[2])/5:up[2] ) end parabol(x) = sum(u->u*u, x) #   fun = parabol plotter(surface, low = [-1 -1], up = [1 1])


我们定义一个实现最速下降法的函数，该方法采用问题的维度，准确性，步长，初始近似值和边界框框架的大小：


 # -- ,     -   function ofGradient(; ndimes = 2, ε = 1e-4, st = 0.9, fit = [9.9, 9.9], low = [-1 -1], up = [10 10]) k = 0 while st > ε g = grad(fit, 0.01) fung = fun(fit) fit -= st*g if fun(fit) >= fung st *= 0.5 fit += st*g end k += 1 #println(k, " ", fit) end #println(fun(fit)) end

您可以专注于根据优化计算梯度方向的函数。


首先想到的是带有矩阵的动作：


 # \delta -      #      function grad(fit, δ) ndimes = length(fit) Δ = zeros(ndimes, ndimes) for i = 1:ndimes Δ[i,i] = δ end fr = [ fun( fit + Δ[:,i] ) for i=1:ndimes] fl = [ fun( fit - Δ[:,i] ) for i=1:ndimes] g = 0.5(fr - fl)/δ modg = sqrt( sum(x -> x*x, g) ) g /= modg end

茱莉亚真正的好处是可以轻松测试问题区域：


 #]add BenchmarkTools using BenchmarkTools @benchmark ofGradient() BenchmarkTools.Trial: memory estimate: 44.14 KiB allocs estimate: 738 -------------- minimum time: 76.973 μs (0.00% GC) median time: 81.315 μs (0.00% GC) mean time: 92.828 μs (9.14% GC) maximum time: 5.072 ms (94.37% GC) -------------- samples: 10000 evals/sample: 1

您可以急于以Sishny风格重新输入所有内容


 function grad(fit::Array{Float64,1}, δ::Float64) ndimes::Int8 = 2 g = zeros(ndimes) modg::Float64 = 0. Fr::Float64 = 0. Fl::Float64 = 0. for i = 1:ndimes fit[i] += δ Fr = fun(fit) fit[i] -= 2δ Fl = fun(fit) fit[i] += δ g[i] = 0.5(Fr - Fl)/δ modg += g[i]*g[i] end modg = sqrt( modg ) g /= modg end @benchmark ofGradient() BenchmarkTools.Trial: memory estimate: 14.06 KiB allocs estimate: 325 -------------- minimum time: 29.210 μs (0.00% GC) median time: 30.395 μs (0.00% GC) mean time: 33.603 μs (6.88% GC) maximum time: 4.287 ms (98.88% GC) -------------- samples: 10000 evals/sample: 1

但事实证明，它本身并没有我们知道应该设置什么类型，所以我们做出了一个妥协：


 function grad(fit, δ) #    ndimes = length(fit) g = zeros(ndimes) for i = 1:ndimes fit[i] += δ Fr = fun(fit) fit[i] -= δ fit[i] -= δ Fl = fun(fit) fit[i] += δ g[i] = 0.5(Fr - Fl)/δ end modg = sqrt( sum(x -> x*x, g) ) g /= modg end @benchmark ofGradient() BenchmarkTools.Trial: memory estimate: 15.38 KiB allocs estimate: 409 -------------- minimum time: 28.026 μs (0.00% GC) median time: 30.394 μs (0.00% GC) mean time: 33.724 μs (6.29% GC) maximum time: 3.736 ms (98.72% GC) -------------- samples: 10000 evals/sample: 1

现在让他画画：


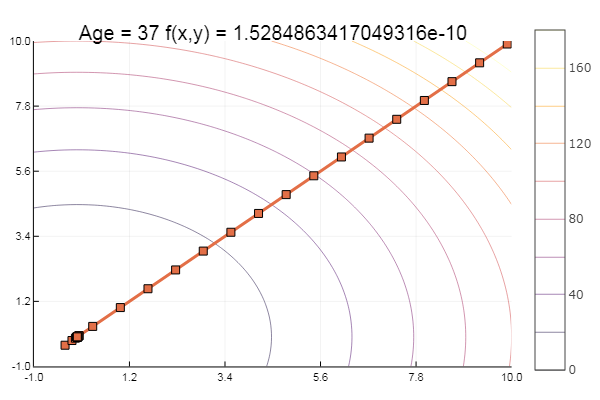
 function ofGradient(; ndimes = 2, ε = 1e-4, st = 0.9, fit = [9.9, 9.9], low = [-1 -1], up = [10 10]) k = 0 x = [] y = [] push!(x, fit[1]) push!(y, fit[2]) plotter(contour, low = low, up = up) while st > ε g = grad(fit, 0.01) fung = fun(fit) fit -= st*g if fun(fit) >= fung st *= 0.5 fit += st*g end k += 1 #println(k, " ", fit) push!(x, fit[1]) push!(y, fit[2]) end plot!(x, y, w = 3, legend = false, marker = :rect ) title!("Age = $kf(x,y) = $(fun(fit))") println(fun(fit)) end ofGradient()


现在让我们尝试Ackley的功能：


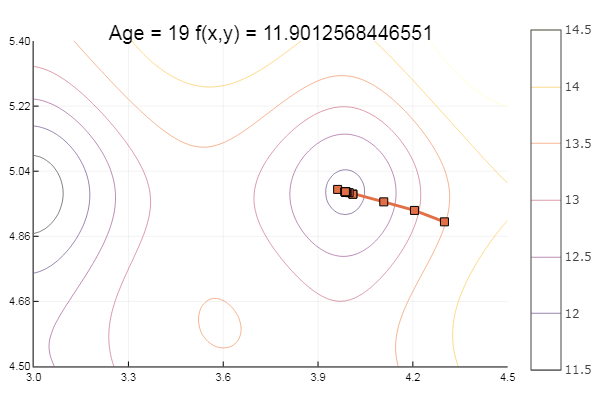
 ekly(x) = -20exp(-0.2sqrt(0.5(x[1]*x[1]+x[2]*x[2]))) - exp(0.5(cospi(2x[1])+cospi(2x[2]))) + 20 + ℯ # f(0,0) = 0, x_i ∈ [-5,5] fun = ekly ofGradient(fit = [4.3, 4.9], st = 0.1, low = [3 4.5], up = [4.5 5.4] )


陷入当地最低要求。 让我们采取更多步骤：


 ofGradient(fit = [4.3, 4.9], st = 0.9, low = [3 4.5], up = [4.5 5.4] ) 


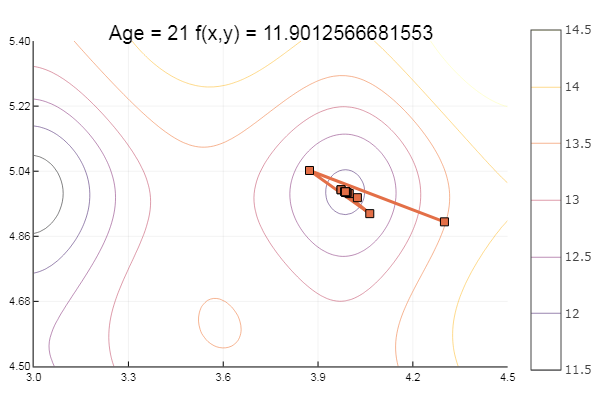
 ofGradient(fit = [4.3, 4.9], st = 1.9, low = [-5.2 -2.2], up = [8.1 7.1] )


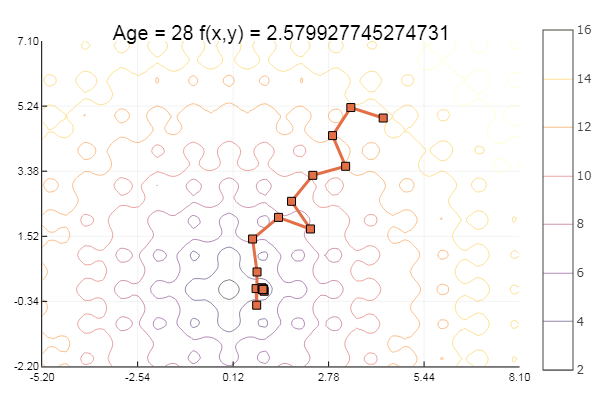
...还有一点：


 ofGradient(fit = [4.3, 4.9], st = 8.9, low = [-5.2 -2.2], up = [8.1 7.1] )


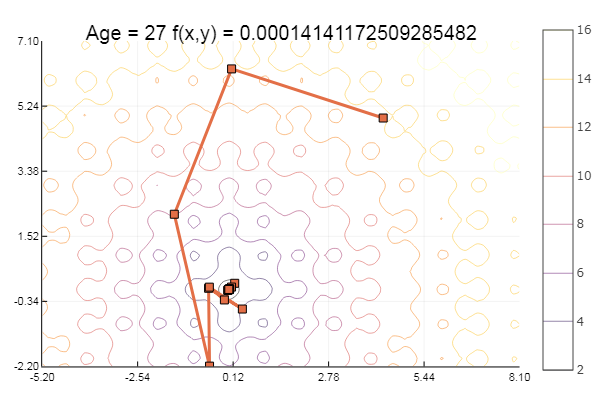
太好了！ 现在有一些沟壑，例如Rosenbrock函数：


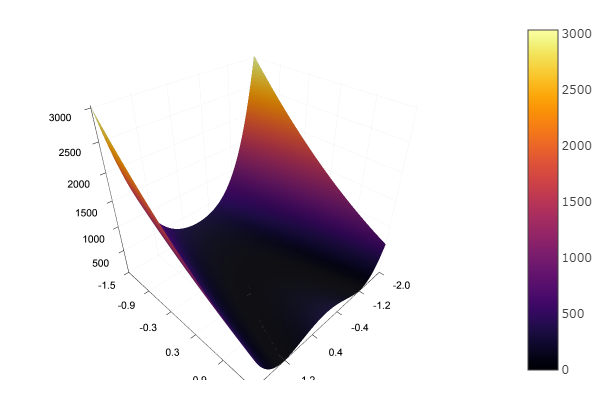
 rosenbrok(x) = 100(x[2]-x[1]*x[1])^2 + (x[1]-1)^2 # f(0,0) = 0, x_i ∈ [-5,5] fun = rosenbrok plotter(surface, low = [-2 -1.5], up = [2 1.5]) 


 ofGradient(fit = [2.3, 2.2], st = 9.9, low = [-5.2 -5.2], up = [8.1 7.1] ) 


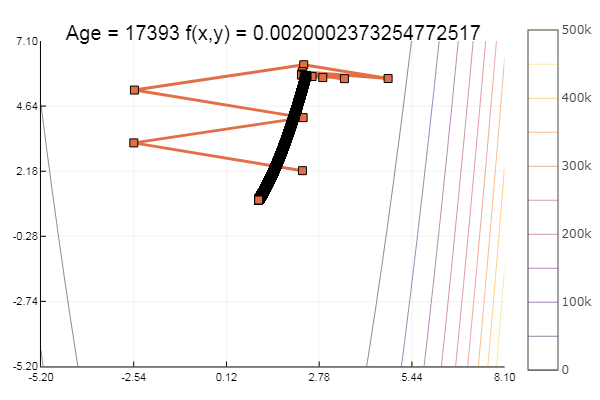
 ofGradient(fit = [2.3, 2.2], st = 0.9, low = [-5.2 -5.2], up = [8.1 7.1] )


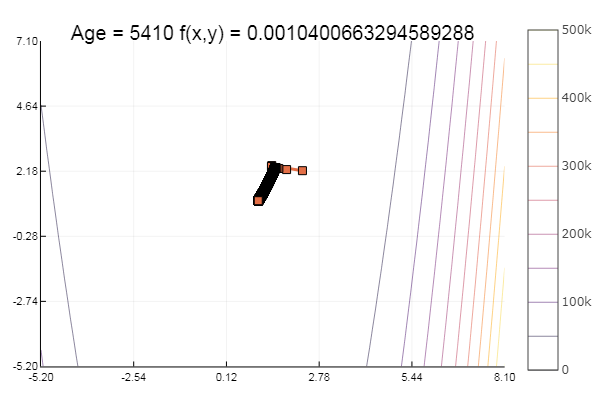
道德：渐变不喜欢檐篷。


单纯形法


Nelder-Mead方法（也称为可变形多面体方法和单纯形方法）是一种无条件优化多个变量函数的方法，该方法不使用函数的导数（更确切地说是梯度），因此很容易适用于非平滑和/或有噪函数。


该方法的本质是单纯形围绕极值点的顺序移动和变形。


该方法找到一个局部极值，并且可能卡在其中一个中。 如果仍然需要查找全局极值，则可以尝试选择其他初始单纯形。


辅助功能：


 #          function sortcoord(Mx) N = size(Mx,2) f = [fun(Mx[:,i]) for i in 1:N] #     Mx[:, sortperm(f)] #Return a permutation vector I that puts v[I] in sorted order. end #   function normx(Mx) m = size(Mx,2) D = zeros(m-1,m) vecl(x) = sqrt( sum(u -> u*u, x) )#   for i = 1:m, j = i+1:m D[i,j] = vecl(Mx[:,i] - Mx[:,j]) #     end D sqrt(maximum(D)) end function simplexplot(xy, low, up) for i = 1:length(xy) if i%11 == 0 low *= 0.05 up *= 0.05 end Xs = range(low[1], stop = up[1], length = 80) Ys = range(low[2], stop = up[2], length = 80) Zs = [ fun([xy]) for y in Ys, x in Xs ] contour(Xs, Ys, Zs) xaxis!( low[1]:(up[1]-low[1])*0.2:up[1] ) yaxis!( low[2]:(up[2]-low[2])*0.2:up[2] ) plot!(xy[i][1,:], xy[i][2,:], w = 3, legend = false, marker = :circle ) title!("Age = $if(x,y) = $(fun(xy[i][:,1]))") savefig("$fun $i.png") end end

和单纯形方法本身：


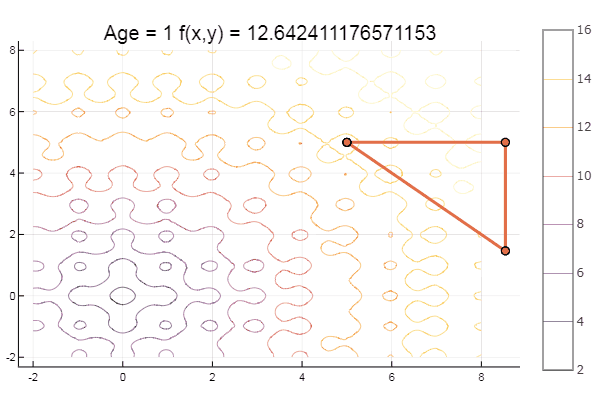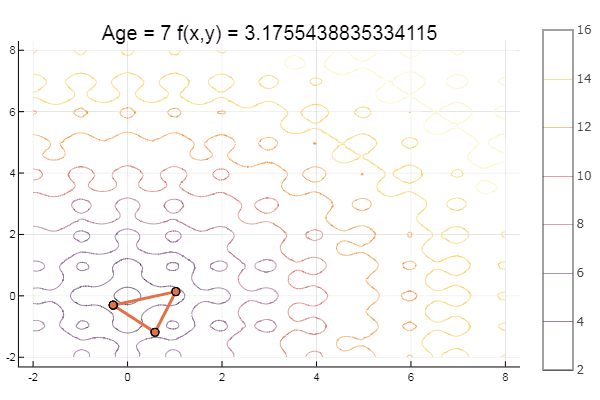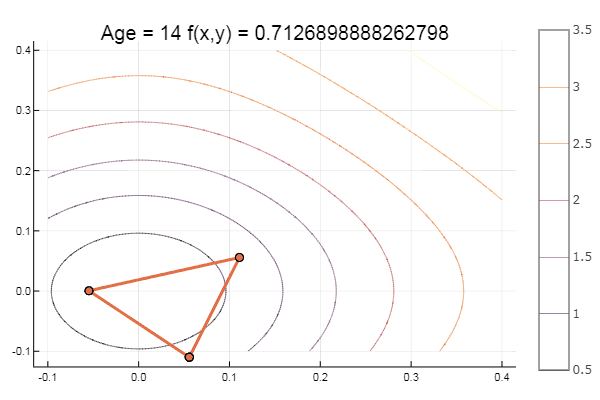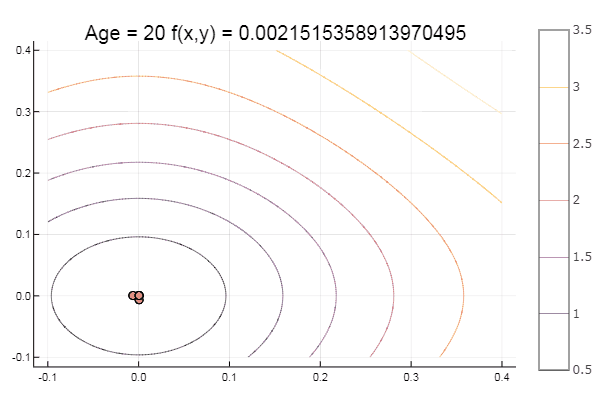
 function ofNelderMid(; ndimes = 2, ε = 1e-4, fit = [.1, .1], low = [-1 -1], up = [1 1]) vecl(v) = sqrt( sum(x -> x*x, v) ) k = 0 N = ndimes Xx = zeros(N, N+1) coords = [] for i = 1:N+1 Xx[:,i] = fit end for i = 1:N Xx[i,i] += 0.5*vecl(fit) + ε end p = normx(Xx) while p > ε k += 1 Xx = sortcoord(Xx) Xo = [ sum(Xx[i,1:N])/N for i = 1:N ] #  - i-  Ro = 2Xo - Xx[:,N+1] FR = fun(Ro) if FR > fun(Xx[:,N+1]) for i = 2:N+1 Xx[:,i] = 0.5(Xx[:,1] + Xx[:,i]) end else if FR < fun(Xx[:,1]) Eo = Xo + 2(Xo - Xx[:,N+1]) if FR > fun(Eo) Xx[:,N+1] = Eo else Xx[:,N+1] = Ro end else if FR <= fun(Xx[:,N]) Xx[:,N+1] = Ro else Co = Xo + 0.5(Xo - Xx[:,N+1]) if FR > fun(Co) Xx[:,N+1] = Co else Xx[:,N+1] = Ro end end end end #println(k, " ", p, " ", Xx[:,1]) push!(coords, [Xx[:,1:3] Xx[:,1] ]) p = normx(Xx) end #while #simplexplot(coords, low, up) fit = Xx[:,1] end ofNelderMid(fit = [-9, -2], low = [-2 2], up = [-8 8])


对于甜点，一些山毛榉...例如，Bukin的功能
f（x，y）=100 sqrt|y−0.01x2|+0.01|x+10|


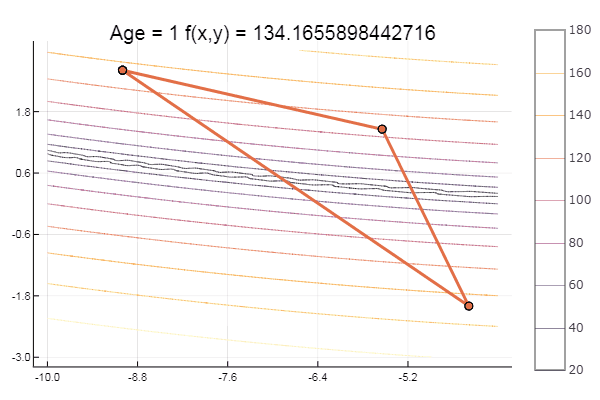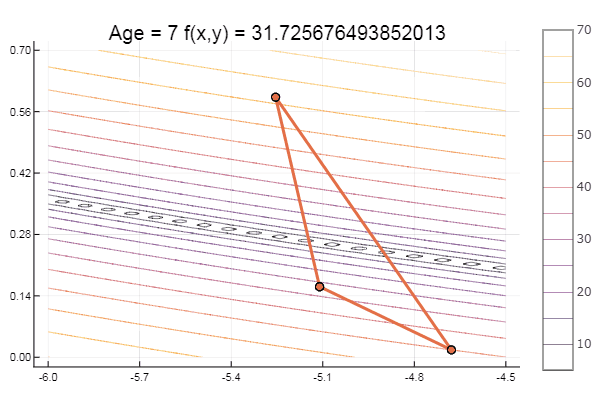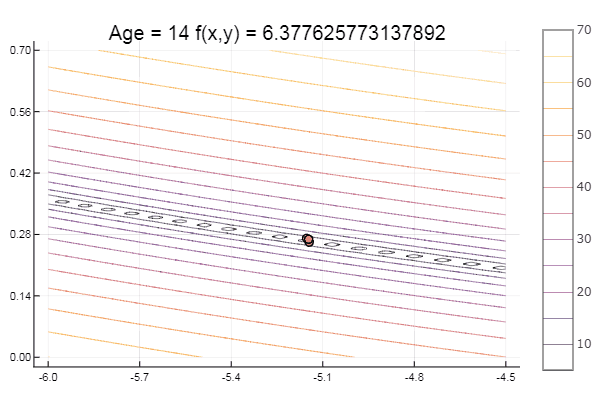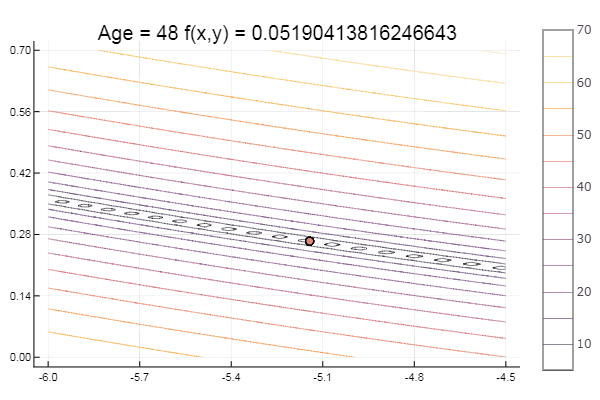
 bukin6(x) = 100sqrt(abs(x[2]-0.01x[1]*x[1])) + 0.01abs(x[1]+10) # f(-10,1) = 0, x_i ∈ [-15,-5; -3,3] fun = bukin6 ofNelderMid(fit = [-10, -2], low = [-3 -7], up = [-8 -4.5])


局部最小值-没什么，主要是选择正确的起始单纯形，因此对我自己来说很喜欢。


红利 Nelder-Mead方法，C ++中最快的下降和坐标下降


报警！ 550行代码！
 /* * File: main.cpp * Author: User * * Created on 3  2017 ., 21:22 */ #include <iostream> #include <math.h> using namespace std; typedef double D; class Model { public: D *fit; D ps; Model(); DI(); }; Model :: Model() { ps = 1; fit = new D[3]; fit[0]=1.3; fit[1]=1.; fit[2]=2.; } D Model :: I() // rosenbrock { return 100*(fit[1]-fit[0]*fit[0]) * (fit[1]-fit[0]*fit[0]) + (1-fit[0])*(1-fit[0]); } class Methods : public Model { public: void ofDescent(); void Newton(int i); void SPI(int i); //sequential parabolic interpolation void Cutters(int i); void Interval(D *ab, D st, int i); void Gold_section(int i); void ofGradient(); void Grad(int N, D *g, D delta); void Srt(D **X, int N); void ofNelder_Mid(); D Nor(D **X, int N); }; void Methods :: ofDescent()//   { int i, j=0; D *z = new D[3]; D sumx, sumz; sumx = sumz = 0; do { sumx = sumz = 0; for(i=0; i<3; i++) z[i] = fit[i]; for(i=0; i<2; i++) { //Cutters(i); //SPI(i); Newton(i); //Gold_section(i); sumx += fit[i]; sumz += z[i]; } j++; //if(j%1000==0) cout << j << " " << fit[0] << " " << fit[1] << " " << fit[2] << " " << fit[3] << endl; //cout << sumz << " " << sumx << endl; } while(fabs(sumz - sumx) > 1e-6); delete[]z; } void Methods :: SPI(int i) { int k = 2; D f0, f1, f2; D v0, v1, v2; D s0, s1, s2; D *X = new D[300]; X[0] = fit[i] + 0.01; X[1] = fit[i]; X[2] = fit[i] - 0.01; while(fabs(X[k] - X[k-1]) > 1e-3) { fit[i] = X[k]; f0 = I(); fit[i] = X[k-1]; f1 = I(); fit[i] = X[k-2]; f2 = I(); v0 = X[k-1] - X[k-2]; v1 = X[k ] - X[k-2]; v2 = X[k ] - X[k-1]; s0 = X[k-1]*X[k-1] - X[k-2]*X[k-2]; s1 = X[k ]*X[k ] - X[k-2]*X[k-2]; s2 = X[k ]*X[k ] - X[k-1]*X[k-1]; X[k+1] = 0.5*(f2*s2 - f1*s1 + f0*s0) / (f2*v2 - f1*v1 + f0*v0); k++; cout << k << " " << X[k] << endl; } fit[i] = X[k]; delete[]X; } void Methods :: Newton(int i) { D dt, T, It; int k=0; while(fabs(T-fit[i]) > 1e-3) { It = I(); T = fit[i]; fit[i] += 0.01; dt = I(); fit[i] -= 0.01; fit[i] -= It*0.001 / (dt - It); cout << k << " " << fit[i] << endl; k++; } } void Methods :: Cutters(int i) { D Tn, Tnm, Tnp, It, Itm; int j=0; Tn = 0.15; Tnm = 2.65;//otrezok Itm = I(); //cout << Tnm << " " << Tn << endl; while(fabs(Tn-Tnm) > 1e-6) { fit[i] = Tn; It = I(); Tnp = Tn - It * (Tn-Tnm) / (It-Itm); cout << j+1 << " " << Tnp << endl; Itm = It; Tnm = Tn; Tn = Tnp; j++; } fit[i] = Tnp; } void Methods :: Interval(D *ab, D st, int i) { D Fa, Fdx, d, c, Fb, fitbox = fit[i]; ab[0] = fit[i]; Fa = I(); fit[i] -= st; Fdx = I(); fit[i] += st; if(Fdx < Fa) st = -st; fit[i] += st; ab[1] = fit[i]; Fb = I(); while(Fb < Fa) { d = ab[0]; ab[0] = ab[1]; Fa = Fb; fit[i] += st; ab[1] = fit[i]; Fb = I(); cout << Fb << " " << Fa << endl; } if(st<0) { c = ab[1]; ab[1] = d; d = c; } ab[0] = d; fit[i] = fitbox; } void Methods :: Gold_section(int i) { D Fa, Fb, al, be; D *ab = new D[2]; D st = 0.5; D e = 0.5*(sqrt(5) - 1); Interval(ab, st, i); al = e*ab[0] + (1-e)*ab[1]; be = e*ab[1] + (1-e)*ab[0]; fit[i] = al; Fa = I(); fit[i] = be; Fb = I(); while(fabs(ab[1]-ab[0]) > e) { if(Fa < Fb) { ab[1] = be; be = al; Fb = Fa; al = e*ab[0] + (1-e)*ab[1]; fit[i] = al; Fa = I(); } if(Fa > Fb) { ab[0] = al; al = be; Fa = Fb; be = e*ab[1] + (1-e)*ab[0]; fit[i] = be; Fb = I(); } cout << ab[0] << " " << ab[1] << endl; } fit[i] = 0.5*(ab[0] + ab[1]); cout << ab[0] << " " << ab[1] << endl; } void Methods :: Grad(int N, D *g, D delta)//   { int n; D Fr, Fl, modG=0; for(n=0; n<N; n++) { fit[n] += delta; Fr = I(); fit[n] -= delta; fit[n] -= delta; Fl = I(); fit[n] += delta; g[n] = (Fr - Fl)*0.5/delta; modG += g[n]*g[n]; } modG = sqrt(modG); for(n=0; n<N; n++) g[n] /= modG; g[N] = I(); } void Methods :: ofGradient() { int n, j=0; D Fun, st, eps; const int N = 2; D *g = new D[N+1]; st = 0.1; eps = 0.000001; while(st > eps) { Grad(N,g,0.0001); for(n=0; n<N; n++) fit[n] -= st*g[n]; Fun = I(); if(Fun >= g[N]) { st /= 2.; for(n=0; n<N; n++) fit[n] += st*g[n]; } j++; cout << j << " " << fit[0]/ps << " " << fit[1]/ps << " " << fit[2]/ps<< endl; } } void Methods :: ofNelder_Mid() { int i, j, k; D modz = 0., p, eps = 1e-3; D FR, FN, F0, FE, FNm1, FC; const int N = 2; D *Co = new D[N]; D *Eo = new D[N]; D *Ro = new D[N]; D *Xo = new D[N]; D **Xx = new D*[N]; D **dz = new D*[N]; for(i=0;i<N;i++) { dz[i] = new D[N]; Xx[i] = new D[N+1]; } for(i=0;i<N;i++) for(j=0;j<N;j++) if(i^j) dz[i][j] = 0; else dz[i][j] = 1; for(i=0;i<N;i++) Xx[i][N] = fit[i]; for(i=0;i<N;i++) modz += fit[i]*fit[i]; modz = sqrt(modz); for(i=0;i<N;i++) dz[i][i] = 0.5*modz; for(i=0;i<N;i++) for(j=0;j<N;j++) Xx[i][j] = fit[i] + dz[i][j]; k = 0; p = Nor(Xx, N); while(p > eps) { k++; Srt(Xx, N); for(i=0;i<N;i++) Xo[i] = 0.; for(i=0;i<N;i++) for(j=0;j<N;j++) Xo[i] += Xx[i][j]; for(i=0;i<N;i++) Xo[i] /= N; for(i=0;i<N;i++) Ro[i] = Xo[i] + (Xo[i]-Xx[i][N]); for(i=0;i<N;i++) fit[i] = Ro[i]; FR = I(); for(i=0;i<N;i++) fit[i] = Xx[i][N]; FN = I(); if(FR > FN) { for(i=0;i<N;i++) for(j=1;j<=N;j++) Xx[i][j] = 0.5*(Xx[i][0] + Xx[i][j]); } else { for(i=0;i<N;i++) fit[i] = Xx[i][0]; F0 = I(); if(FR < F0) { for(i=0;i<N;i++) Eo[i] = Xo[i] +2*(Xo[i] - Xx[i][N]); for(i=0;i<N;i++) fit[i] = Eo[i]; FE = I(); if(FE < FR) for(i=0;i<N;i++) Xx[i][N] = Eo[i]; else for(i=0;i<N;i++) Xx[i][N] = Ro[i]; } else { for(i=0;i<N;i++) fit[i] = Xx[i][N-1]; FNm1 = I(); if(FR <= FNm1) for(i=0;i<N;i++) Xx[i][N] = Ro[i]; else { for(i=0;i<N;i++) Co[i] = Xo[i] +0.5*(Xo[i] - Xx[i][N]); for(i=0;i<N;i++) fit[i] = Co[i]; FC = I(); if(FC < FR) for(i=0;i<N;i++) Xx[i][N] = Co[i]; else for(i=0;i<N;i++) Xx[i][N] = Ro[i]; } } } for(i=0;i<N;i++) cout << Xx[i][0] << " "; cout << k << " " << p << endl; p = Nor(Xx, N); if(p < eps) break; } for(i=0;i<N;i++) fit[i] = Xx[i][0]; /*for(i=0;i<N;i++) { for(j=0;j<N+1;j++) cout << Xx[i][j] << " "; cout << endl; }*/ delete[]Co; delete[]Xo; delete[]Ro; delete[]Eo; for(i=0;i<N;i++) { delete[]dz[i]; delete[]Xx[i]; } } //   D Methods :: Nor(D **X, int N) { int i, j, k; D norm, xij, pn = 0.; for(i=0;i<N;i++) for(j=i+1;j<=N;j++) { xij = 0.; for(k=0;k<N;k++) xij += ( (X[k][i]-X[k][j])*(X[k][i]-X[k][j]) ); pn = sqrt(xij);//    if(norm > pn) norm = pn;//   } return sqrt(norm); } //    void Methods :: Srt(D **X, int N) { int i, j, k; D temp; D *f = new D[N+1]; D *box = new D[N]; D **y = new D*[N+1]; for(i=0;i<N+1;i++)//  y[i] = new D[N+1]; for(i=0;i<N;i++) box[i] = fit[i];//    for(i=0;i<=N;i++) { for(j=0;j<N;j++) fit[j] = X[j][i]; f[i] = I();//     } for(i=0;i<N;i++) fit[i] = box[i];//    for(i=0;i<N;i++) for(j=0;j<=N;j++) y[i][j] = X[i][j]; for(i=0;i<=N;i++) y[N][i] = f[i];//stack(X, f) //    , //     N    for(i=1;i<=N;i++) for(j=0;j<=Ni;j++) if(y[N][j] >= y[N][j+1]) for(k=0;k<=N;k++) { temp = y[k][j]; y[k][j] = y[k][j+1]; y[k][j+1] = temp; } //submatrix   for(i=0;i<N;i++) for(j=0;j<=N;j++) X[i][j] = y[i][j]; /* for(i=0;i<=N;i++) { for(j=0;j<=N;j++) cout << y[i][j] << " "; cout << endl; } */ for(i=0;i<N+1;i++) delete[]y[i]; delete[]box; delete[]f; } int main() { Methods method; //method.ofDescent(); //method.ofGradient(); method.ofNelder_Mid(); return 0; }

今天足够了。 下一步是合乎逻辑的，尝试进行全局优化，输入更多测试函数，然后使用内置方法研究软件包。

Source: https://habr.com/ru/post/zh-CN440070/

More articles:


All Articles