朱莉娅和一群粒子

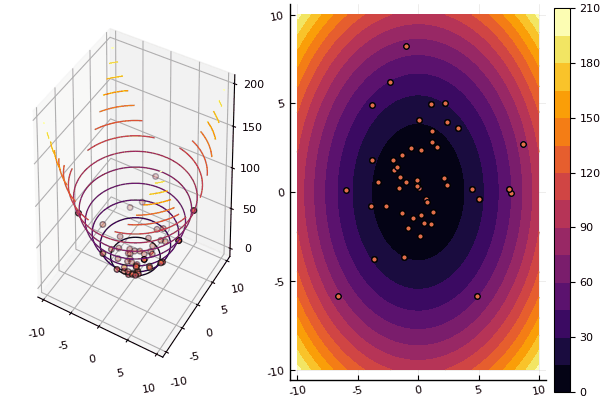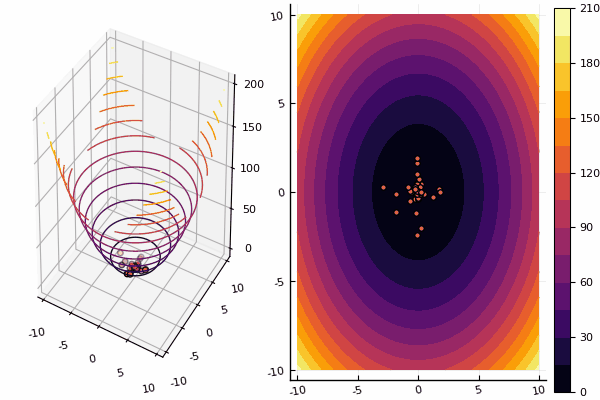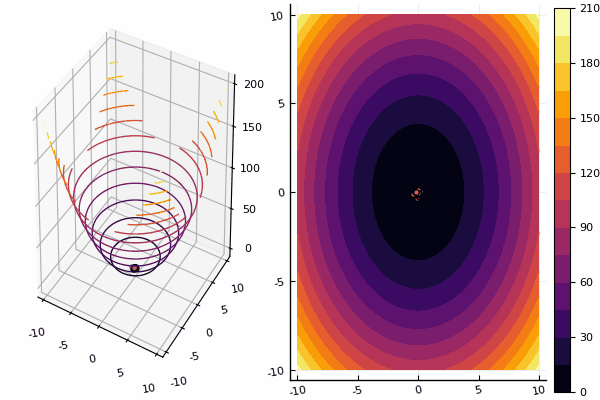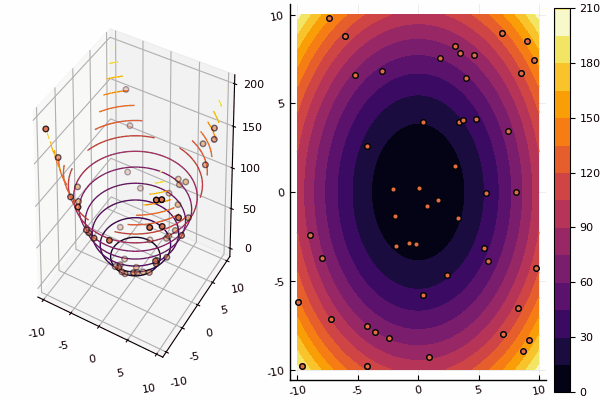
我们将继续研究多维优化的方法，其次是粒子群方法，它会寻找全局最小值。

理论

• 维基百科
• 各种粒子群方法及其拓扑
• Python和C＃中的大量粒子
• 一包密封件的优化方法

该算法非常简单：

每个粒子在特定时刻的位置由以下公式计算：

哪里 $$$p_i$-协调特定粒子的最佳解决方案， $$$g_i$-这个时代所有粒子的最佳解决方案的坐标， $$$C_p$和 $$$C_g$-加权因子（为特定模型选择）， $$$A_c$是惯性系数，它可以取决于一个时代的数目，那么粒子的速度就会平稳地变化。

测试功能

由于很高兴了解该方法的工作原理，因此我们将获得更多测试功能：

parabol(x) = sum(u->u*u, x) # f(0,0) = 0, x_i ∈ [-10,10] shvefel(x) = sum(u-> -u*sin(sqrt(abs(u))), x) # f(420.9687,420.9687) = -819?, x_i ∈ [-500,500] rastrigin(x) = 10*length(x) + sum(u->u*u-10*cos(2*pi*u), x) # f(0,0) = 0, x_i ∈ [-5,5] ekly(x) = -20exp(-0.2sqrt(0.5(x[1]*x[1]+x[2]*x[2]))) - exp(0.5(cospi(2x[1])+cospi(2x[2]))) + 20 + ℯ # f(0,0) = 0, x_i ∈ [-5,5] rosenbrok(x) = 100(x[2]-x[1]*x[1])^2 + (x[1]-1)^2 # f(0,0) = 0, x_i ∈ [-5,5] bill(x) = (1.5-x[1]+x[1]*x[2])^2 + (2.25-x[1]+x[1]*x[2]*x[2])^2 + (2.625-x[1]+x[1]*x[2]^3)^2 # f(3,0.5) = 0, x_i ∈ [-5,5] boot(x) = (x[1]+2x[2]-7)^2 + (2x[1]+x[2]-5)^2 # f(1,3) = 0, x_i ∈ [-10,10] bukin6(x) = 100sqrt(abs(x[2]-0.01x[1]*x[1])) + 0.01abs(x[1]+10) # f(-10,1) = 0, x_i ∈ [-15,-5; -3,3] levy13(x) = sinpi(3x[1])^2 + (1+sinpi(3x[2])^2)*(x[1]-1)^2 + (1+sinpi(2x[2])^2)*(x[2]-1)^2 # f(1,1) = 0, x_i ∈ [-10,10] himmelblau(x) = (x[1]^2+x[2]-11)^2 + (x[1]+x[2]^2-7)^2 # f(3,2)... = 0, x_i ∈ [-5,5] camel3humped(x) = 2x[1]^2 - 1.05x[1]^4 + x[1]^6 /6 + x[1]*x[2] + x[2]^2 # f(0,0) = 0, x_i ∈ [-5,5] izom(x) = -cos(x[1])*cos(x[2])*exp(-( (x[1]-pi)^2 + (x[2]-pi)^2 )) # f(π,π) = -1, x_i ∈ [-100,100] holdertable(x) = -abs(sin(x[1])*cos(x[2])exp(abs( 1-sqrt(x[1]^2+x[2]^2)/pi ))) # f(±8.05502,±9.66459) = -19.2085, x_i ∈ [-10,10] shaffer4(x) = 0.5 + (cos(sin(abs(x[1]^2-x[2]^2)))^2-0.5) / (1+0.001(x[1]^2+x[2]^2))^2 # f(0,1.25313) = 0.292579, x_i ∈ [-100,100] 

而且，事实上，MRC本身：

 function mdpso(; nparts = 50, ndimes = 2, ages = 50, #   lover = [-10 -10], upper = [10 10], C1 = [1.9 1.9], #  - C2 = [1.8 1.8], Ac = [0.1 0.1], ) minind = 0 V = zeros(nparts,ndimes) #   n  n X = zeros(nparts,ndimes) funmin = -Inf Fmin = Inf Fbest = fill(Fmin, nparts) funx = zeros(nparts) xmem = zeros(nparts,ndimes) xbest = zeros(ndimes) #   #      for i in 1:nparts, j in 1:ndimes X[i,j] = randomer(lover[j], upper[j]) end for i in 1:ages for j in 1:nparts funx[j] = fun(X[j,:]) if funx[j] < Fbest[j] Fbest[j] = funx[j] xmem[j,:] = X[j,:] end end #      ploter(lover, upper, X, funx, i); funmin = minimum(funx) minind = argmin(funx) if funmin < Fmin Fmin = funmin xbest[:] = X[minind,:] end for j in 1:nparts, k in 1:ndimes R1 = rand() R2 = rand() V[j,k] = Ac[k]*V[j,k] + C1[k]*R1*(xmem[j,k] - X[j,k]) + C2[k]*R2*(xbest[k] - X[j,k]) X[j,k] += V[j,k] end println("Age № $i\n xbest:\n $(xbest[1]) $(xbest[2])") println("Fmin: $Fmin\n") end f = open("$fun.txt","w") #      write(f,"C1 = $C1, C2 = $C2, Ac = $Ac, lower = $lover, upper = $upper, ages = $ages, parts = $nparts") close(f) end 

但是，对于工程图，计算会花费更长的时间，但会更加美观：

 using Plots pyplot() function ploter(l, u, xy, z, n_age ) contour(Xs, Ys, Zs, fill = true); #    (   ) #   ,       scatter!(xy[:,1], xy[:,2], legend = false, xaxis=( (l[1], u[1])), yaxis=( (l[2], u[2])) ); #savefig("$fun $n_age.png") #        end fun = bill low = [-4 -4] up = [4 4] Xs = range(low[1], stop = up[1], length = 80) Ys = range(low[2], stop = up[2], length = 80) Zs = [ fun([xy]) for y in Ys, x in Xs ] surface(Xs, Ys, Zs) xaxis!( (low[1], up[1]), low[1]:(up[1]-low[1])/5:up[1] ) yaxis!( (low[2], up[2]), low[2]:(up[2]-low[2])/5:up[2] ) 

 mdpso(C1 = [1.2 1.2], C2 = [1.1 1.1], Ac = [0.08 0.08], lower = [-4 -4], upper = [4 4], ages = 30) 

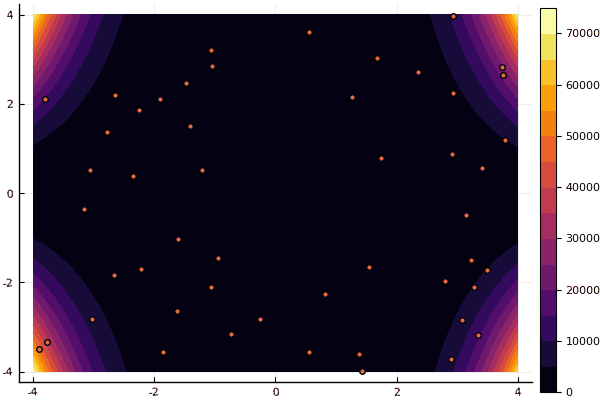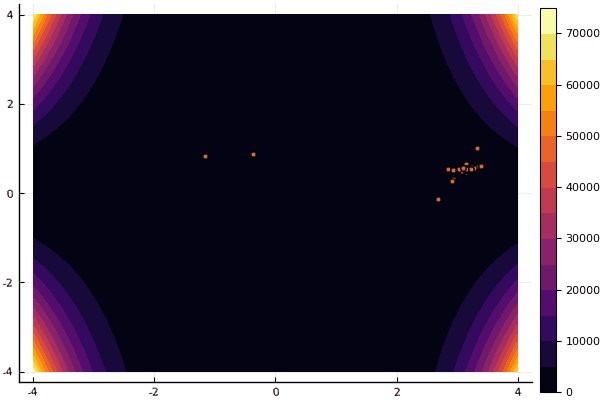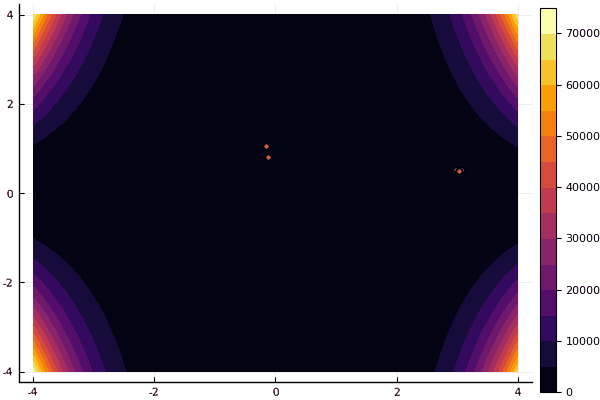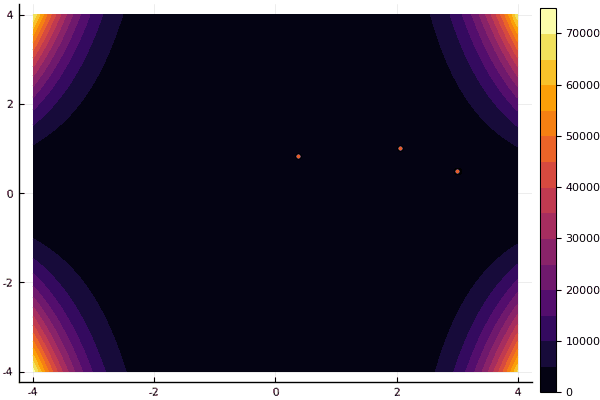
 fun = ekly mdpso(C1 = [1.7 1.7], C2 = [1.7 1.7], Ac = [0.07 0.07], lower = [-5 -5], upper = [5 5], ages = 15) 

 fun = himmelblau mdpso(C1 = [1.1 1.1], C2 = [1.0 1.0], Ac = [0.09 0.09], lower = [-5 -5], upper = [5 5], ages = 20, parts = 50) 

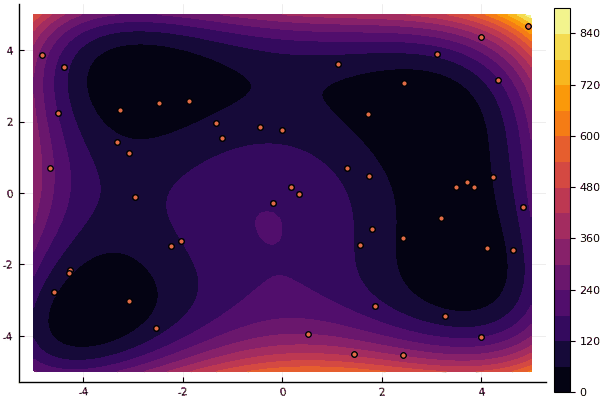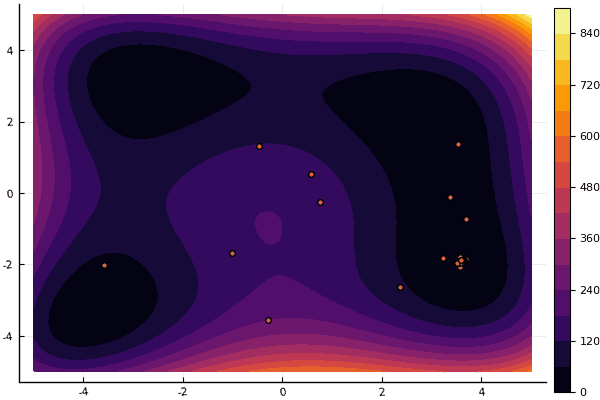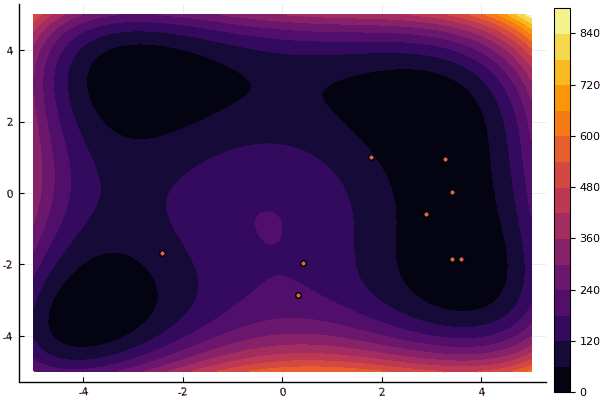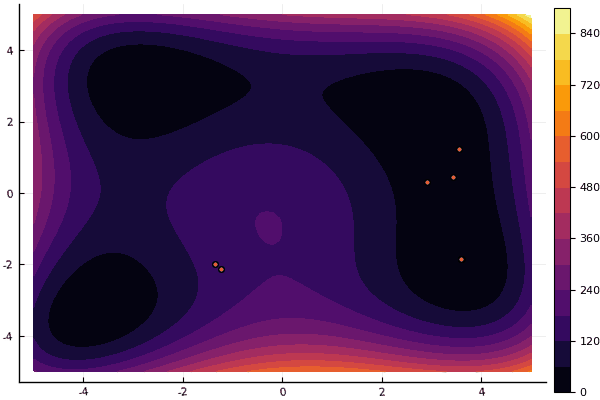
 fun = holdertable mdpso(C1 = [1.1 1.1], C2 = [1.0 1.0], Ac = [0.09 0.09], lower = [-10 -10], upper = [10 10], ages = 20, parts = 50) 

 fun = levy13 mdpso(C1 = [1.1 1.1], C2 = [1.0 1.0], Ac = [0.09 0.09], lower = [-10 -10], upper = [10 10], ages = 20, parts = 50) 

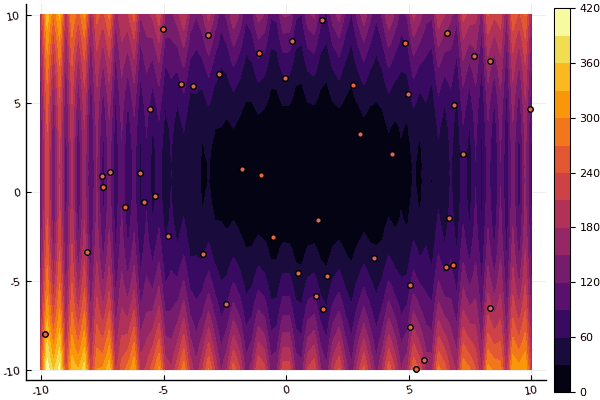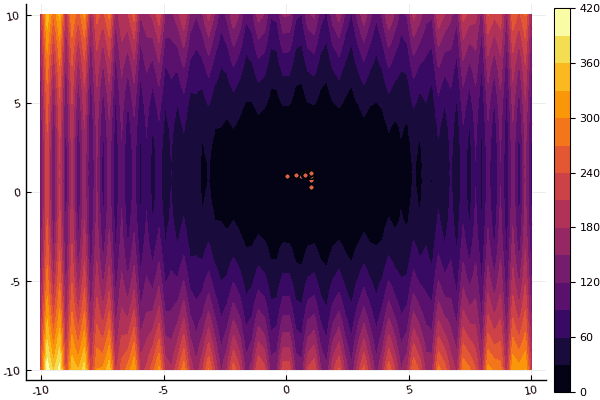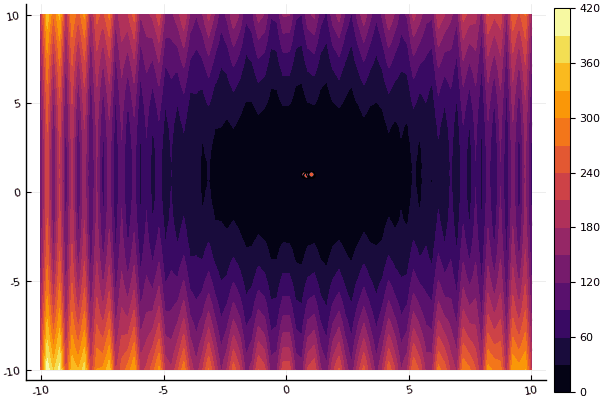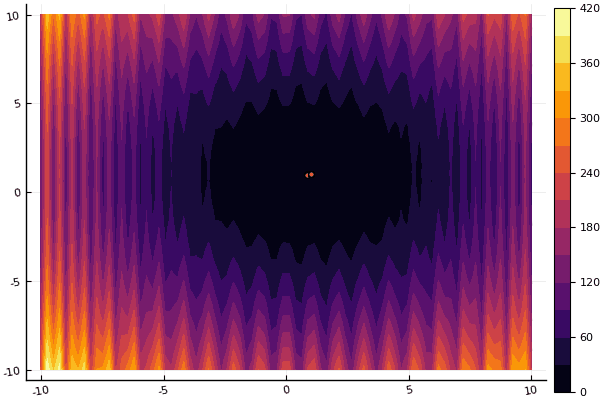
 fun = shaffer4 mdpso(C1 = [1.1 1.1], C2 = [1.0 1.0], Ac = [0.09 0.09], lower = [-100 -100], upper = [100 100], ages = 20, parts = 50) 

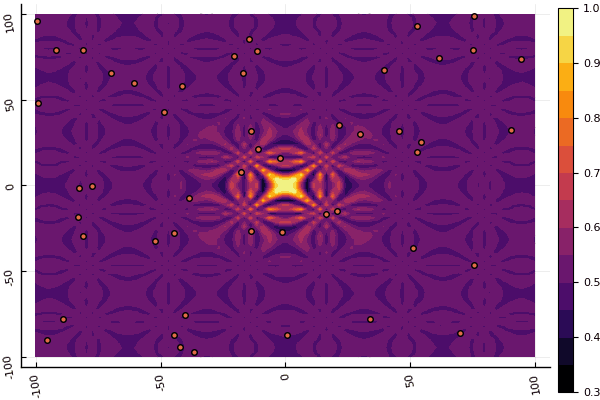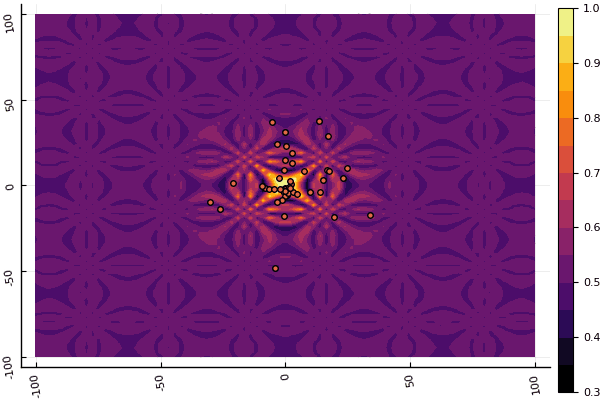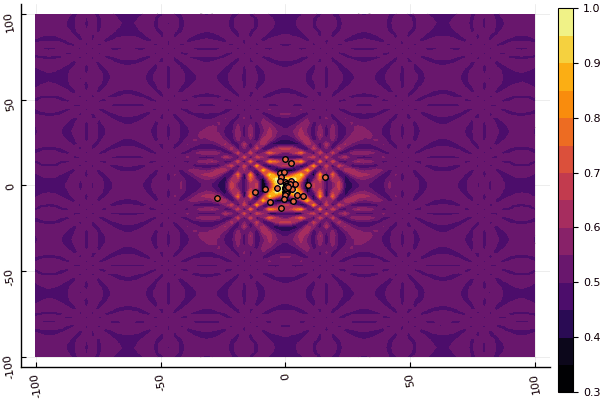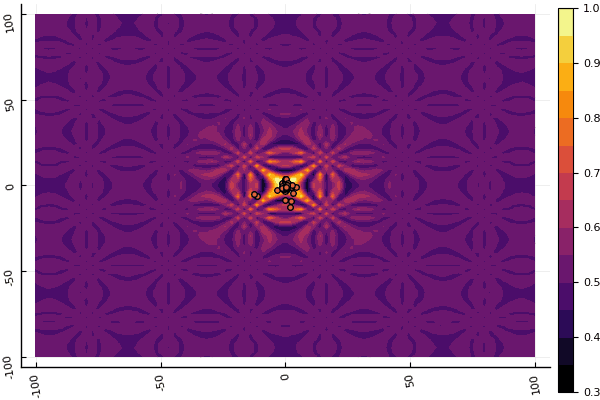
真正令人沮丧的是，对参数和随机性元素大惊小怪：如果没有一个粒子在全局最小值附近飞行，那么这整个事物可能会落入局部：

 fun = rastrigin mdpso(mdpso(C1 = [0.1 0.1], C2 = [1 1], Ac = [0.08 0.08], lover = low, upper = up, ages = 30)) 

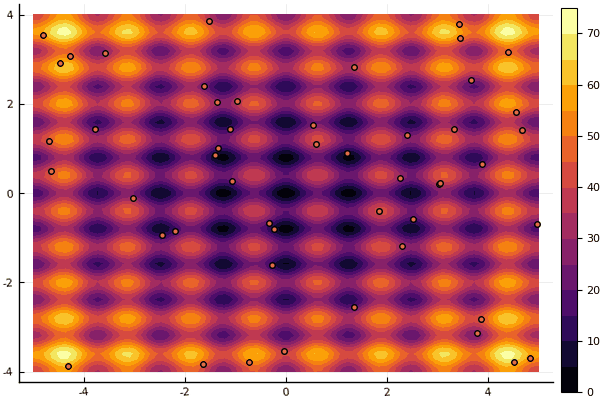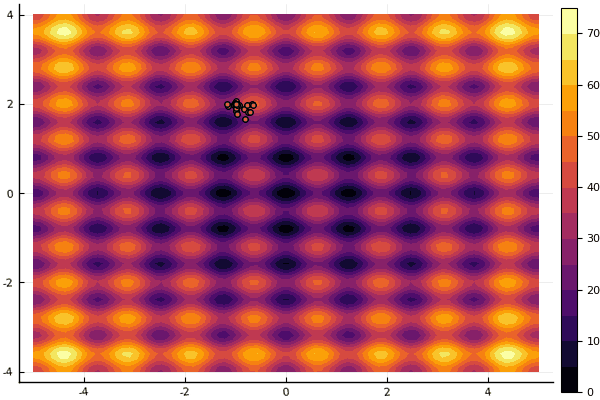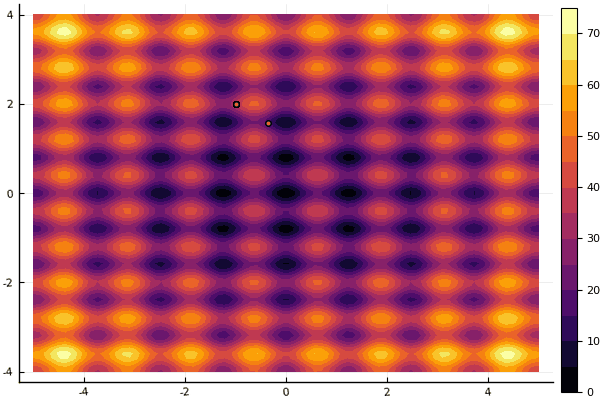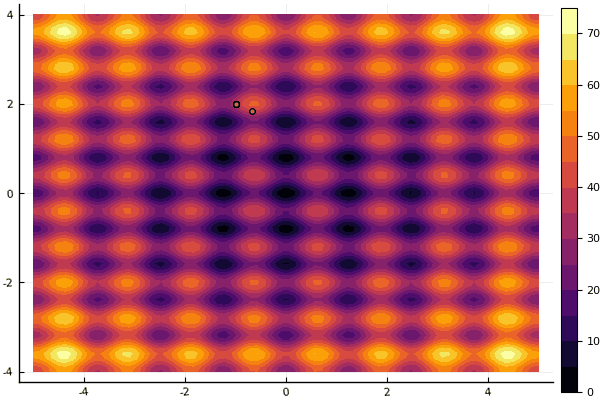
是的，老 不太 好的Rosenbrock仍然无法理解：

 fun = rosenbrok mdpso(C1 = [1.7 1.7], C2 = [1.5 1.5], Ac = [0.15 0.15], lover = low, upper = up, ages = 20, nparts = 50) ... Age № 20 xbest: 0.37796421341886866 0.12799160066705667 Fmin: 0.409026370833564 

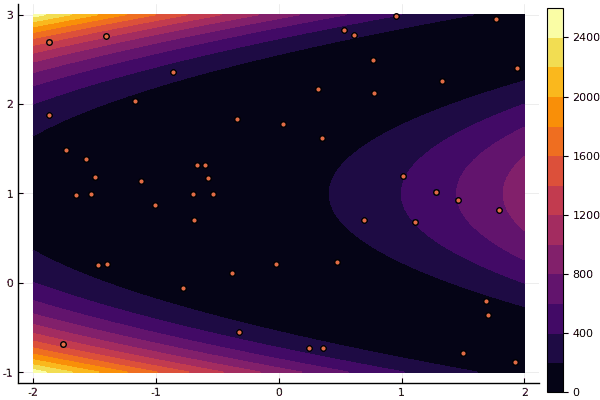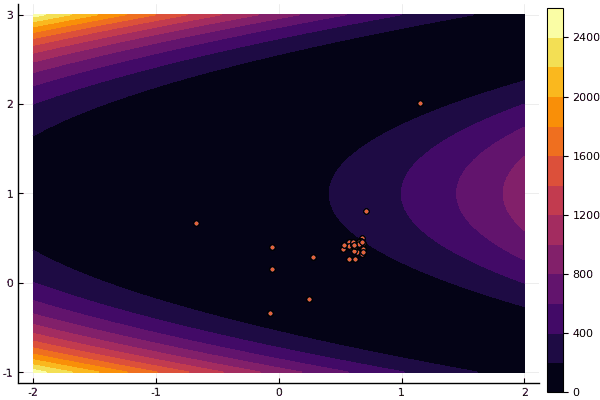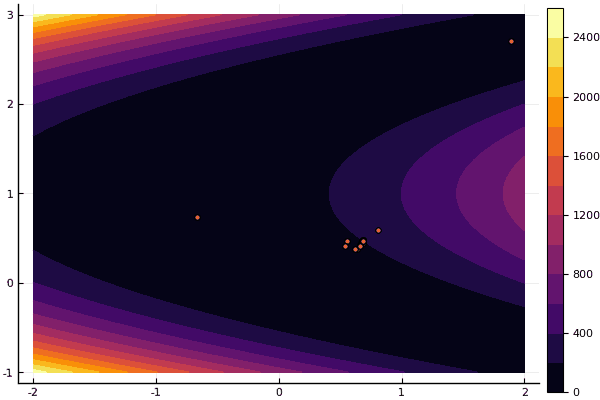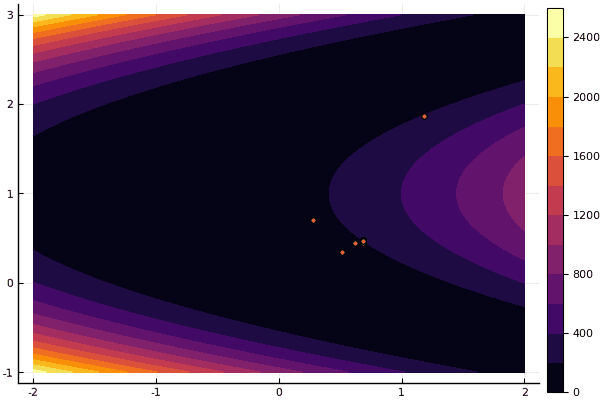
但是正如我之前所说，您可以使用FDM搜索近似于全局最小值的近似值，然后指定Nelder-Mead：

 vecl(x) = sqrt( sum(u -> u*u, x) ) function sortcoord(Mx) N = size(Mx,2) f = [fun(Mx[:,i]) for i in 1:N] #     Mx[:, sortperm(f)] end function normx(Mx) m = size(Mx,2) D = zeros(m-1,m) for i = 1:m, j = i+1:m D[i,j] = vecl(Mx[:,i] - Mx[:,j]) #     end D sqrt(maximum(D)) end function ofNelderMid(; ndimes = 2, ε = 1e-4, fit = [.1, .1], low = [-1 -1], up = [1 1]) k = 0 N = ndimes Xx = zeros(N, N+1) for i = 1:N+1 Xx[:,i] = fit end for i = 1:N Xx[i,i] += 0.5*vecl(fit) + ε end p = normx(Xx) while p > ε k += 1 Xx = sortcoord(Xx) Xo = [ sum(Xx[i,1:N])/N for i = 1:N ] #  - i-  Ro = 2Xo - Xx[:,N+1] FR = fun(Ro) if FR > fun(Xx[:,N+1]) for i = 2:N+1 Xx[:,i] = 0.5(Xx[:,1] + Xx[:,i]) end else if FR < fun(Xx[:,1]) Eo = Xo + 2(Xo - Xx[:,N+1]) if FR > fun(Eo) Xx[:,N+1] = Eo else Xx[:,N+1] = Ro end else if FR <= fun(Xx[:,N]) Xx[:,N+1] = Ro else Co = Xo + 0.5(Xo - Xx[:,N+1]) if FR > fun(Co) Xx[:,N+1] = Co else Xx[:,N+1] = Ro end end end end println(k, " ", p, " ", Xx[:,1]) p = normx(Xx) end #while fit = Xx[:,1] end 

 ofNelderMid(fit = [0.37796 0.127992]) ... 92 0.00022610400555036366 [1.0, 1.0] 93 0.00015987967588703512 [1.0, 1.0] 94 0.00011305200343052599 [1.0, 1.0] 2-element Array{Float64,1}: 0.9999999996645973 0.9999999995466575 

对于经典的MFC，停止标准并不是一目了然的：最佳点可以保留多个时代的位置，某些粒子之间的距离也不能长时间保持不变。 因此，使用了时代数的限制。 为了增加找到全局最小值的机会，有必要增加粒子和历元的数量，这在内存和时间方面都非常昂贵（不要开玩笑，每次迭代中每个维调用50次目标函数）。

品德

• 如果您不希望或无法使用复杂的现代方法，则可以使用更简单的方法组合
• 很多时候，对于问题，有一种狭窄的方法（例如，针对山沟功能）
• 建议手头有几个不同的MO，以便进行一致的比较
• 并非总是可以将您的任务放到方法中并立即获得正确的答案-您应该花时间研究，更改参数，如果看不到浮雕，则至少应打印出中间计算值以跟踪收敛。

今天就这些了，谢谢您的关注，并祝大家一切顺利！