零知识证明/论据是一种新兴的加密技术,有望使我们更接近区块链的圣杯:提供数据隐私和可审计性。
零知识的潜在应用包括但不限于:
零知识证明的另一个应用是帮助区块链
扩展 。 ZKP允许在不牺牲安全性的情况下“压缩”区块链交易的计算。
在本文中,我们描述了如何使用Bitfury的Exonum平台将零知识(特别是Bulletproofs )应用于构建以隐私为中心的服务。
态势分析
可以使用“围墙花园”方法在区块链应用中实现
某种程度的数据隐私,该方法隐藏了数据,因为在防火墙,基于角色的访问控制,
护城河和其他外围安全措施的帮助下,对数据的访问受到限制。 可以对区块链中的敏感数据进行加密(也许使用公钥加密方案,并使用由同一区块链管理的相关公钥)和/或存储在区块链外部(在这种情况下,区块链仅存储哈希指纹)。数据)。 许多许可的分布式分类帐框架中都使用了这种方法。
但是,“围墙花园”方法的弊端变得越来越明显。 坦率地说,这种方法与区块链的主要卖点之一-可审计性是相反的。 如果无法通过咨询智能合约逻辑来审核区块链上的数据,则区块链将成为光荣的
链接时间戳服务。 区块链上有一些数据的事实不再意味着该数据按照智能合约规则有效。 围墙花园方法的第二个主要缺点是它无法缩放。 例如,R3的CTO理查德·布朗(Richard Brown)将他们解决方案的隐私模型与Slack频道
进行了恰当的
比较 -很难从花园中安全地添加或删除参与者,甚至在没有事先对参与者数量和身份的期望时,更是如此参与者。
这就是
零知识可能很有价值的地方。 通过设计,零知识证明和论点¹令人信服地证明了有关私有数据的声明,而除了要证明的声明外,没有透露任何有关数据的信息。 可以轻松地使零知识证明得到
普遍验证,而又不牺牲任何隐私!²此功能正是构建同时保护隐私和可审核的系统所需要的。
我们的研究
为了演示零知识证明的使用,我们将构建一个加密货币服务,其功能与
Exonum文档中的教程服务类似。 该服务可以注册用户和钱包(提供初始代币余额作为奖励)并在注册方之间转移代币。 借助内置在Exonum服务中的数字签名密码系统Ed25519,可以对所有交易进行身份验证。 我们没有隐藏交易方的身份(即,他们的公钥),但是我们隐藏了正在交易的代币数量以及系统中每个帐户的余额。 我们还将在本文结尾处讨论如何改善隐藏交易实体的服务。
该服务是完全开源的,可以在
此处访问。
密码学背景
为了了解服务的工作方式,我们首先需要向我们介绍支持Bulletproofs的核心加密原语-一种称为
Pedersen承诺的概念。 密码承诺方案有点像哈希函数:有人输入秘密数据(开头)并获得无法识别的加密输出(承诺)。 然后可以揭露该空缺以证明承诺值与其对应。
哈希函数与哈希函数的区别在于,除了具有
约束力 (没有人可以设计出两个产生相同承诺的不同空缺)之外,一个承诺方案也有望被
隐藏 (不可能反转方案并在给定承诺的情况下产生一个空缺)。 如果哈希函数的输入在整个输入空间上均匀分布,则该哈希函数将隐藏,但是这种假设最不适合承诺(实际上,必须可以从很小的集合(如布尔值)中承诺一个值。 这样,除了有效载荷之外,该开口还包含
致盲因子 ,该
致盲因子使得(至少在统计上)不可能在给定承诺的情况下猜测有效载荷。
Pedersen承诺方案使用
素数阶组和两个生成器
G和
H组成了
素数组,其中
离散对数问题 (DLP)被认为很难
。 G和
H的选择必须使它们之间的离散对数关系未知。 换句话说,没人知道
k使得
H = kG.³开口是一对
(x,r) ,其中
x是承诺值,
r是致盲因子; 两者都是组标量(基本上,“溢出”的整数类似于大多数编程语言中使用的有限整数类型)。 承诺计算为
Comm(x; r)= xG + rH 。 可以证明,如果组中的DLP很困难,那么Pedersen的承诺将在计算上具有约束力并完美地隐藏起来。
Pedersen承诺的关键属性是它们是可加的:2个承诺的总和(或差额)是对承诺值的总和(或差额)的承诺。 的确
C1 = x1 G + r1 H; C2 = x2 G + r2 H => C1 + C2 = (x1 + x2) G + (r1 + r2) H = Comm(x1 + x2; r1 + r2).
我们在此处不包含有关如何构建和验证防弹措施的详细信息,但是可以在以下资源中找到更多信息-[
1 ]和[
2 ]。 足以注意到,上限
M被假定为具有形式
2 ^(2 ^ n) ,这导致最有效的证明构造。
建立服务
凭借我们的知识,我们可以借助Pedersen承诺安全地隐藏帐户余额和转账金额。 使用范围证明,我们可以证明/验证转移是正确的:
对于第一个证明,我们对转账金额
C_a进行承诺(它直接存在于转账交易中),并验证在
C_a-Comm(1; 0)中提交的值在
[0,M)范围内。 实际上,这等效于证明
C_a对应于
[1,M]范围内的值。 发送人可以出示此证明,因为他/她知道转账金额
a 。
对于第二个证明,我们需要承担发送方当前余额
C_s的承诺,并验证
C_s-C_a中提交的值在
[0,M)范围内。 再次,发送者可以产生此证明为s /他知道
C_s和
C_a都
打开 。
为了将转移应用于
区块链状态,我们从发送方的余额承诺中减去金额承诺
C_a (正如我们已经验证的那样,它不会导致负余额或发送方余额的增加),然后将
C_a添加到接收方的余额中平衡承诺。
关键细节
重要的是要注意,有一些条件会使实施的服务变得更加复杂。
汇款的接收者必须从某个地方找出
C_a的空缺 ; 否则,他/她将不再知道自己的余额开口,并且不能再用他的钱包做任何事情。 在转移交易的明文(即整个要点)中不存在开仓。 我们
可以假设接收方通过链外通道(例如,发送方通过电报发送的)可靠地获得了开门机会,但这不是示例性的情况。 因此,我们改为使用基于Diffie-Hellman密钥交换的两方公共密钥加密来加密开放内容(libsodium称为这种类型的加密
盒 )。 为了增加好处,
Box例程所需的Curve25519密钥可以从Ed25519密钥转换而来,因此我们可以继续为每个用户使用一个密钥对,而不是引入单独的加密密钥。

引入加密后,我们将无法再自动应用传输。 的确,发送者可以恶意或无意地提供垃圾而不是开放加密,而区块链逻辑将无法判断是否是这种情况。⁶因此,我们要求接收者通过单独的交易明确接受转移。
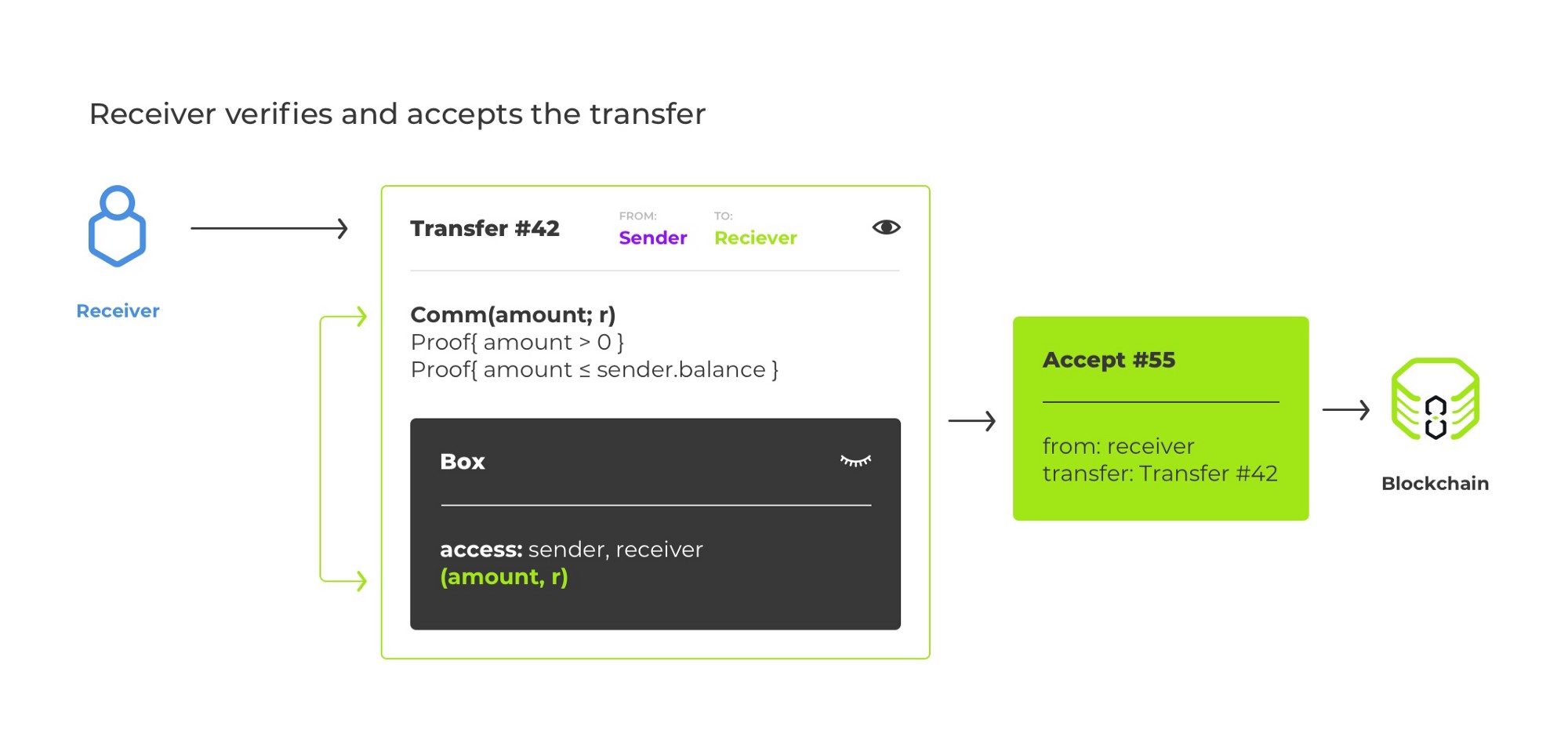
在接受转帐之前,它会修改发件人的余额承诺(否则,我们将允许双倍支出!),但收款人的则不会。

一旦接受交易被区块链网络确认,接收方的余额就会更新,并且转移完成。

为了防止死锁,传输为接收者指定一个时间延迟(以相对的区块链高度为单位,
即比特币的
CSV ),以使接收者发出接受信号。 如果时间锁定已过期,则传输将自动退还给发件人(Exonum通过
Service :: beforeCommit()挂钩允许此操作)。
另一个问题更加复杂。 为了提供足够的余额证明,发送者需要知道他/她的当前余额,但情况并非总是如此。 零星的接受交易或退款可能会不经意间增加发送者的余额; 在这种情况下,传输将无法通过验证,并且发件人将受到合理的挫败。
为了缓解这个问题,我们允许转账参考发送者认为他/她当前钱包状态的信息(更确切地说,该参考采用改变帐户余额的事件数量的形式(转账和退款)。 在检查足够余额的证明时,我们使用参考状态来获取发件人的余额承诺。 此外,我们检查自引用状态以来没有发生任何外发转账。 如果是这种情况,我们可以肯定的是,如果从发件人的
当前余额中减去转帐金额,我们将得到一个非负值。 实际上,参考点之后的帐户历史记录中的事件(传入的转账和退款)只能增加余额!
有了参考点后,发件人仍然受到一些限制。 s /创建新传输时,他必须没有挂起的传输。 但是,此限制比转移时知道一个帐户状态的要求要少得多。 从根本上说,我们使发送者依赖于他
/她先前的行为,而不取决于其他人的行为。
实作
我们使用纯
Rust编写的防弹库,该库最近已达到
预发行阶段 。 由于Exonum平台是用Rust编写的,因此可以与库无缝集成。 另外,与原始白皮书中描述的防弹版本(用
C语言开发,并使用比特币的secp256k1椭圆曲线)不同,我们使用的库基于Curve25519,该库已在Exonum中用作它的主要组件。 ED25519数字签名密码系统
基于以上描述实现服务非常简单。 最困难的部分是构造Merkle证明,以验证返回给用户的信息,从而使他们不必盲目地信任与之通信的Exonum节点。 在这方面,改善服务开发人员的经验是
Exonum 1.0版本的主要目标之一。
后续步骤
我们构建的服务不会隐藏传输的发送者和接收者的身份,这是现实应用程序的主要限制。 幸运的是,有一些方法可以解决此问题。
zCash中使用的通用技术(但主要适用于其他用例,例如
Ethereum )基于创建系统状态的
Merkle树 。 例如,zCash构建了
票据承诺树 ,该
树大致相当于比特币中曾经创建的交易输出。 然后,零知识证明将在此树中包含身份验证路径(也称为Merkle分支),从而揭示出与该树元素有关的内容,而没有揭示所引用的元素。 这种方法的缺点是,用于构建Merkle树的加密哈希函数很难转移到零知识领域。 结果证明在计算上变得昂贵-单个证明可能需要几秒钟甚至几分钟来创建。 寻找更多“ ZKP友好”的密码哈希函数是积极研究的领域。
如果我们接受其他限制,则可能会有更简单的解决方案。 例如,
Narula等人的最新论文。 描述了具有有限的先验已知数量的参与者的系统,该参与者可以在彼此之间进行交易而无需透露参与者或任何交易的转移金额。 (想想一个针对隐私的区块链网络来进行银行间转账。)
更为平淡的是,开发的服务可能会享受许多技术改进:更多的测试范围,签名和加密密钥的分离,基准测试等。 服务UX的一项重大改进是可以对来自同一用户的事务进行确定性排序,我们计划在发布Exonum 1.0后不久解决该问题。
结论
我们已经描述了如何构造一个具有零隐私证明(特别是防弹证据)的,具有较强隐私性的基于帐户的加密令牌。 令牌逻辑被实现为Exonum服务。 尽管目前该服务仅是概念的证明,但它展示了Exonum平台如何用于以执行环境所产生的非常低的开销来构建复杂的加密基元之上。
- 证明和论点之间有一个复杂的区别,我们在这里不再赘述。 为了简单起见,我们将本文中的所有零知识结构称为零知识证明,即使从理论角度来看这并不总是正确的。
- 这可以通过一种称为Fiat-Shamir变换的非常通用的技术来完成,该技术将交互式证明协议转换为非交互式,可普遍验证的协议。 再次牺牲科学严谨性,我们将不会明确阐明我们使用的零知识证明是非交互式的。
- 发电机通常采用“无所作为”的方法来选择。 例如,G可能是其在公钥密码学中使用的组规范的一部分,并且H是通过散列函数H〜hash(G)从G派生的。
- 后者意味着即使是具有无限计算能力的对手也无法推断出承诺的内容。 实际上,如果组中的DLP被破坏,则每个承诺都可以打开为任何可能的值。
- 这部分是概念验证的决定; 通常,出于不同目的重用密钥是一个坏主意。
- 从理论上讲,可以为加密值等于承诺余额的情况提供零知识证明; 但是,这将极大地增加系统的复杂性。
- 值得一提的是,一些违反“自参考状态以来没有外发转移”规则的转移仍然是正确的; 我们只是无法验证这一点。