如果您尚未阅读有关该主题的第一篇文章,建议您从开始。
既然我提到了对金融数学家的一种肯定的态度,尽管是非常间接的,所以让我根据“风险分析”中该主题的发展方式将其发展到荒谬的程度。 在计算期权价格时,他们通常会考虑该价格对一组参数的敏感性。 例如,当发行期权的股票价格发生变化,或者股票价格的波动性或中央银行的利率发生变化时,期权价格将如何变化。
我们可能对赢得点数的概率发生变化时赢得游戏的概率的变化感兴趣。 实际上,我们要计算从一阶到二阶的导数。 最简单的方法是从图中通过肉眼对其进行评估。 可以看出,在50:50的情况下达到了最大值。 如果赢得积分的几率从0.45变为0.55,则羽毛球获胜的可能性将从0.26增加到0.74,即增加0.48。 粗略估算得出的导数约为5。即,如果您以相等的机会成长到0.51(即51%),则赢得游戏的可能性将增加约0.05(或5%)。 同样,您可以在图表上的任何其他点计算导数。
在金融中,通常使用“碰撞并运行”方法,即,它们会少量更改参数并计算新的期权价格和衍生工具。 采取类似的操作后,我在图表上引用了准确的数据(我将更改以百分比表示,虽然有点粗鲁,但在这种情况下可以接受)。 为了更加清晰起见,他增加了5分和31分的比赛。 顺便说一句,在冬季两项比赛中,最多可以考虑5人参加聚会。这并不是绝对的类比,因为总的拍摄次数是固定的。 但是解决方法几乎相同。
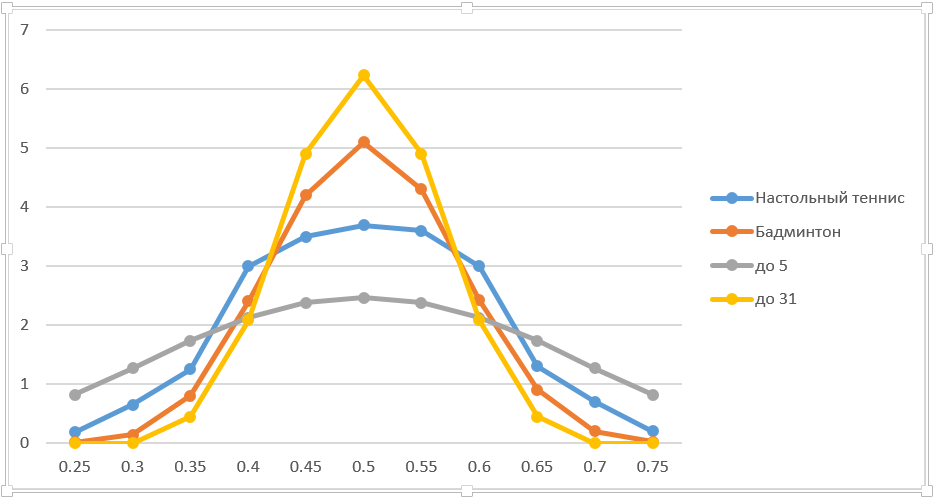
显然,批次越长,在50:50时的导数越高。 如果聚会的长度趋于无穷大,那么即使是最小的利益,也可以保证玩家的胜利。 曲线的宽度相应减小。 总的来说,结论是显而易见的。
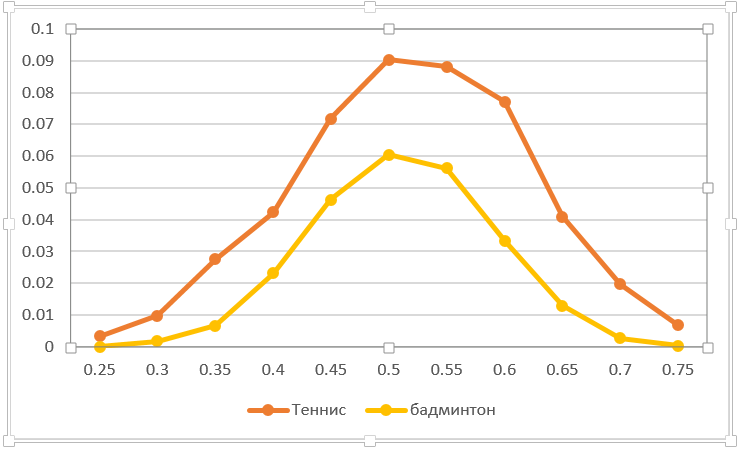
您可以计算出对一点意外放电的敏感度。 例如,喂入网中。 一张纸牌会在多大程度上影响比赛的结果? 实际上,这是将对手的获胜分数降低了一个百分点。 下图反映了这种情况。 自然地,在乒乓球中,丢分比在羽毛球中更重要。 在相等的作用力下,游戏结果的可能性尽可能地降低-从0.5降至0.41。 注意曲线的不对称性(不同于其他大多数曲线)。 这不是巧合。 事实是,平衡失误从50:50转移到赢得积分的可能性更高,因为失去的积分会使玩家的机会变差。
让我们提出另一个有趣的经验。 想象一下,其中一名玩家可以集中精力玩高于平均水平(p1 +增量)的3分。 假设在此之后,对齐方式将恢复为原始对齐方式(达到预期的平均值,而不考虑“强度波动”)。 显然,获胜的可能性将会增加。 问题是,什么时候集中注意力-在游戏开始还是结束时都重要? 我建议在进一步阅读之前做一个假设。
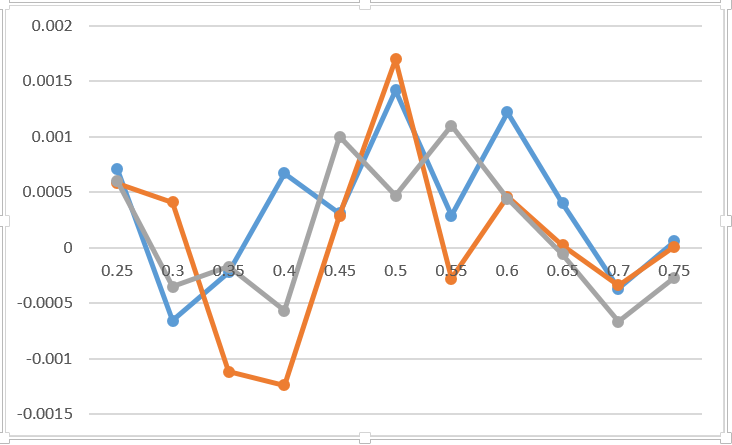
因此,如实验所示,完全专注时绝对没有区别(没有考虑道德计划的因素)。 该图显示了在专注于游戏的3个不同位置的情况下赢得比赛的概率与专注于前3个点的概率之间的差异。 我认为这张图反映了蒙特卡洛的错误,仅此而已。 我为第一个玩家的平局结果加了0.2,共3次平局。 我什至没有在图表上指出哪条线对应哪个选项。 它绝对不会改变任何东西。 关于此主题的唯一有价值的建议是在为时已晚之前做好准备。
现在,让我们考虑如果其中一个参与者具有稳定性会发生什么。 神经是神经,负责任的游戏会发生。 假设他平均获得相同百分比的分数,但是绘制特定点时,该百分比浮动。 例如,一半的点以概率p1 +德尔塔,而另一半则以p1-德尔塔。 在这种情况下,平均值p1保持原始值,+δ或-δ的损失随机发生,概率为0.5。 它会以某种方式影响游戏的结果吗? 正如我在蒙特卡洛(Monte Carlo)的帮助下进行的实验所显示的,几乎没有发现差异。 实际上,尽管随机地增加或减少一定数量,我们仍然保持赢得积分的平均概率相同。 该建议本身表明,分布曲线不会影响游戏的结果,而只会影响平均值,但我不会自己考虑。 在这里你必须思考。
我还想导出一个微分方程,例如金融领域的Black Scholes,以完成关联。 确定重要的导数,将随机成分归零。我们还需要处理离散性。 也许我会把这留给真正的金融数学家。