与克鲁格，苏格拉底和知识圈共事

我长期以来一直专注于知识的话题。 因此，我遇到了苏格拉底的格言-“我知道我什么都不知道”，并带有Dunning-Krueger效应。 我对这些概念的真实性感到放心。 我看到了他们的关系。 此外，我有信心，您可以在数学上证明Dunning-Krueger效应的存在。

邓宁-克鲁格效应

邓宁-克鲁格效应是一种元认知畸变，其特征在于，资历水平低的人会得出错误的结论，做出的决定失败，同时由于资历水平低而无法识别自己的错误。

以下是演示“催款-克鲁格”效果的简化图形。

该图显示了邓宁-克鲁格效应，并没有为我们提供任何解释。 但这只是给我们希望，希望您能走出绝望谷。 该图形非常平滑，并且相对较好地反映了现实。 对于心理学而言，这样的时间表几乎是足够的。 有时这是令人误解的。 例如，根据时间表进行评估，一旦离开绝望之谷，您将永远不会回到它。 在实践中，事实证明您回来不止一次。 但是，这样的时间表是进一步研究的良好起点。

函数图是一种数学工具，也许有些函数可以帮助我们在数学上证明效果本身的表现。

苏格拉底

邓宁-克鲁格效应在某种程度上呼应了苏格拉底的格言：“我知道我一无所知。”

类似的想法可以追溯到其他思想家的著作，他们可以自己阅读。

表达式的含义可以如下所示：我们想象我们所有的知识都是球的内部，而无知则是球的外部。 我们的知识越多，球的表面积就越大，因此我们的“接触”就变得无知。

知识圈

在我看来，谈论知识之球是正确的。 但是“知识之球”这个词听起来有点不科学。 用知识圈代替知识球。 或更确切地说，知识圈。 有四个这样的圈子：

1. 我知道
2. 我知道我不知道。 有意识的未知。
3. 我不知道我不知道。 这就是人类的全部知识。
4. 绝对的知识。

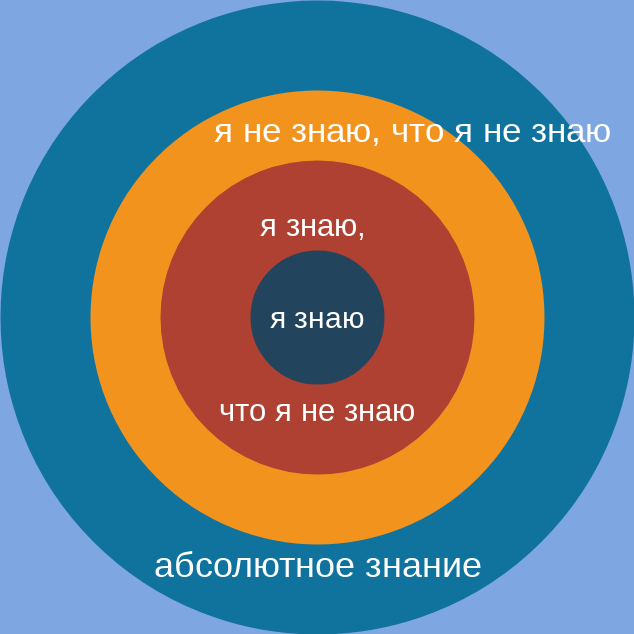
每个外圆完全包括内圆。

3和4个圆对于全人类都是相同的。 每个人分别有1个和2个圈子。

通常，第一个圆的膨胀有助于第二个圆的膨胀。 第二个圆的每次扩展都会使我们更接近第三个圆的边界。 如果第二个圆圈的增长率大大高于第一个圆圈的增长率，则一个人不可避免地会陷入Dunning-Kruger效应图上的绝望谷。

Dunning-Krueger效应的数学证明

让我们看看一个人在认知过程中会发生什么以及这与Dunning-Krueger效应如何相关。

名称

• K1 =我知道。
• K2 =我知道我不知道。 有意识的未知。
• K3 =我不知道我不知道。 这就是人类的全部知识。
• K4 =绝对知识。

新手

K1非常小。 K2略大于K1。

在认知过程中，K1的增长快于K2。

胡说八道

K1赶上了K2。 K2离K3很远。

绝望之谷

K2增长非常快。 从很小的项目切换到大型项目，参加会议或开始收听播客后，就会发生这种情况。

K1跟不上K2的增加。

立即清楚地知道要离开绝望山谷需要做什么。 有必要注入现有知识（K1）。 您可以限制K2的增长。 如果您在绝望之谷绝对不舒服，应该有意识地这样做。 就个人而言，我很乐意提及苏格拉底，并留在绝望谷。

您需要了解，即使在这个山谷中也没有停滞。 您的知识量仍在增长。 但是有意识的未知数也在增长（K2）。 感觉就像你住在这个山谷。 但是，继续您的开发。 然后K1将开始追赶K2并进入启蒙坡道。

启蒙坡

K1的增长速度快于K2。

要使K1的增长快于K2的增长，您需要执行以下操作：

1. 开始更深入地探索您的区域。
2. 选择较窄的专业。
3. 限制K2增长
   
   • 停止收听播客
   • 停止参加会议
   • 降档。

方式1-2是好的。 在存在心理问题的情况下应使用方法3。

稳定高原

K1赶上了K2。 这已经在愚蠢的顶峰发生了。

从愚蠢峰开始的稳定高原仅在K2和K3之比上有所不同。 在稳定高原上，K2应该非常接近K3。 但是，认识到这一点并不容易。 确实，在前一阶段，K2的增长对我们来说非常有限。 仔细看看。

正确的时间表使您对自己的知识充满信心

该图显示了信心对自己知识的依赖性。 它看起来像是Dunning-Kruger效应的图形，但是会有所不同。

假设对知识的信心等于一个人自己的知识量与第二个循环的知识量之比（K1 / K2）。 这两个参数都会随时间变化。

图表上的线：

• 蓝线表示对自己知识的信心。
• 红线显示第二个知识圈的大小。
• 绿线表示第二个圆圈的知识量和其自身知识（K2-K1）量之间的差异。
  您可以在此处查看带有数据和图形的表。

结论

自信功能如下所示：

知识信心= K1 / K2。
其中K1自己的知识，而K2自觉的未知。

您可以走出绝望谷。 但是您可以比第一次有了更多的知识。

真正推动科学进步的人们永远都在绝望谷，因为他们...