👿 👨🏻‍🌾 ❔ 朱莉娅和优化 💃 💇🏼 🏂🏾

是时候考虑提供解决优化问题方法的软件包了。很多问题可以减少到找到某些功能的最小值，因此您应该在军械库中有两个或两个求解器，甚至还有一个完整的软件包。

参赛作品

朱莉娅语言继续流行。在https://juliacomputing.com上，您可以了解为什么天文学家，机器人技术和金融家选择这种语言；在https://academy.juliabox.com上，您可以开始免费课程，以学习该语言并将其用于任何类型的机器学习中。对于那些认真决定要开始学习的人，我建议您观看视频，阅读文章并在https://julialang.org/learning/上单击Jupiter笔记本电脑，或者至少从下而上浏览集线器：这里将提供安装，功能以及业务应用程序紧急的。现在让我们进入库。

黑药

BlackBoxOptim -Julia的全局优化包（ http://julialang.org/ ）。它支持多用途和单用途优化问题，并且侧重于（元）启发式/随机算法（DE，NES等），与更传统的确定性算法相比，该算法不需要优化的函数是可区分的，通常基于梯度/可微性。它还支持并行计算，以加快对缓慢评估的功能的优化。

下载并连接库

]add BlackBoxOptim using BlackBoxOptim

设置Rosenbrock函数：

 f(x) = (1.0 - x[1])^2 + 100.0 * (x[2] - x[1]^2)^2

我们正在为二维问题的每个坐标寻找最小间隔（-5; 5）：

 res = bboptimize(f; SearchRange = (-5.0, 5.0), NumDimensions = 2)

答案如下：

 Starting optimization with optimizer DiffEvoOpt{FitPopulation{Float64},RadiusLimitedSelector,BlackBoxOptim.AdaptiveDiffEvoRandBin{3},RandomBound{RangePerDimSearchSpace}} 0.00 secs, 0 evals, 0 steps Optimization stopped after 10001 steps and 0.12400007247924805 seconds Termination reason: Max number of steps (10000) reached Steps per second = 80653.17866385692 Function evals per second = 81628.98454510146 Improvements/step = 0.2087 Total function evaluations = 10122 Best candidate found: [1.0, 1.0] Fitness: 0.000000000

和大量无法读取的数据，但发现的数据最少。由于使用的是随机的，因此函数调用会很多，因此对于多维任务，最好使用方法选择

 function rosenbrock(x) return( sum( 100*( x[2:end] - x[1:end-1].^2 ).^2 + ( x[1:end-1] - 1 ).^2 ) ) end res = compare_optimizers(rosenbrock; SearchRange = (-5.0, 5.0), NumDimensions = 30, MaxTime = 3.0);

凸面

凸面是Julia的“学科凸面编程”包（学科凸面编程？）。 Convex.jl可以通过MathProgBase接口使用包括Mosek，Gurobi，ECOS，SCS和GLPK在内的各种求解器来求解线性程序，混合整数线性程序和与DCP兼容的凸程序。它还支持使用复杂变量和系数进行优化。

 using Pkg #      Pkg.add("Convex") Pkg.add("SCS")

该站点上有很多示例：层析成像（通过在分布区域上给定的积分来恢复密度分布的过程。例如，您可以在黑白图像中使用层析成像），最大化熵，逻辑回归，线性编程等。

例如，您需要满足以下条件：

开 始 ＆ ＆ ＆ ＆

$\开始{array} {ll} \ mbox {satisfy}＆\ | x \ | _2 \ leq 100 \\＆e ^ {x_1} \ leq 5 \\＆x_2 \ geq 7 \\＆\ sqrt {x_3 x_4} \ geq x_2 \ end {array}$

 using Convex, SCS, LinearAlgebra x = Variable(4) p = satisfy(norm(x) <= 100, exp(x[1]) <= 5, x[2] >= 7, geomean(x[3], x[4]) >= x[2]) solve!(p, SCSSolver(verbose=0)) println(p.status) x.value

会给出答案

 Optimal 4×1 Array{Float64,2}: 0.0 8.554892320716046 15.329934133156783 15.329934133156783

跳

JuMP是Julia内置的特定领域的数学优化语言。他目前支持许多开放式和商用求解器（Artelys Knitro，BARON，Bonmin，Cbc，Clp，Couenne，CPLEX，ECOS，FICO Xpress，GLPK，Gurobi，Ipopt，MOSEK，NLopt，SCS）。

JuMP可以轻松地在没有专家知识的情况下识别和解决优化问题，但同时，它还允许专家实施高级算法，例如在线性编程中使用有效的“热”启动或使用回调与分支和边界求解器进行交互。 JuMP的速度也很快-基准测试表明它可以以类似于AMPL之类的专用商业工具的速度处理计算，同时又能保持高级通用编程语言的表现力。 JuMP可以轻松地集成到复杂的工作流程中，包括模拟和Web服务器。

该工具使您可以处理以下任务：

LP =线性编程
QP =二次编程
SOCP =二阶圆锥规划（包括凸二次约束和/或目的问题）
MILP =混合整数线性规划
NLP =非线性规划
MINLP =混合整数非线性规划
SDP =半定义编程
MISDP =混合整数半定编程

仅需几篇文章，对其功能的分析就足够了，因此现在让我们继续以下内容：

最佳

Optim有许多求解器可以从免费和商业渠道获得，并且已经封装了许多求解器以供Julia使用。他们中很少有人用这种语言写的。在性能方面，这很少有问题，因为它们通常是用Fortran或C语言编写的。但是，直接用Julia编写的求解器确实有一些优势。

在编写需要进行某些优化的Julia软件（软件包）时，程序员可以编写自己的优化过程，也可以使用许多可用的求解器之一。例如，它可能来自NLOpt集中。这意味着添加一个不是用Julia编写的依赖项，您需要对用户所在的环境进行更多的假设。用户是否有适当的编译器？我可以在项目中使用GPL代码吗？

的确，使用用C或Fortran编写的求解器无法使用Julia的主要优点之一：多重调度。由于Optim是用Julia完全编写的，因此我们目前可以使用调度系统来简化自定义预设的使用。这个方向的计划功能是允许用户驱动的算法各个阶段的求解器选择，完全基于调度而不是Optim开发人员选择的预定义功能。

Julia上的软件包还意味着Optim可以通过JuliaDiff中的软件包访问自动区分功能。

导游

继续：

 ]add Optim using Optim #   f(x) = (1.0 - x[1])^2 + 100.0 * (x[2] - x[1]^2)^2 x0 = [0.0, 0.0] optimize(f, x0)

我们通过一个方便的报告得到答案：

 Results of Optimization Algorithm * Algorithm: Nelder-Mead #   * Starting Point: [0.0,0.0] * Minimizer: [0.9999634355313174,0.9999315506115275] * Minimum: 3.525527e-09 * Iterations: 60 * Convergence: true * √(Σ(yᵢ-ȳ)²)/n < 1.0e-08: true * Reached Maximum Number of Iterations: false * Objective Calls: 118

并与我的Nelder Mead进行比较！

扰流板

我的会慢一些:(

藏起来

 using BenchmarkTools @benchmark optimize(f, x0) BenchmarkTools.Trial: memory estimate: 11.00 KiB allocs estimate: 419 -------------- minimum time: 39.078 μs (0.00% GC) median time: 43.420 μs (0.00% GC) mean time: 53.024 μs (15.02% GC) maximum time: 59.992 ms (99.83% GC) -------------- samples: 10000 evals/sample: 1

在检查过程中，还发现如果使用初始近似值（0，0），则我的实现无法正常工作。作为停止条件，可以使用单纯形的体积，但是我使用由顶点组成的矩阵的范数。在这里，您可以阅读有关规范的几何解释。在这两种情况下，都将获得零矩阵-退化矩阵的特殊情况；因此，该方法不执行任何步骤。您可以配置起始单纯形的创建，例如，通过设置其顶点到初始近似值的距离（与我的近似值不同（不像我的向量长度的一半，fu，太可惜了……）），那么方法设置将更加灵活，或者确保所有顶点都没有坐在某一点：

  for i = 1:N+1 Xx[:,i] = fit end for i = 1:N Xx[i,i] += 0.5*vecl(fit) + ε end

好吧，我的单纯形goraaazdo比较慢：

 ofNelderMid(fit = [0, 0.]) step= 118 7.7234e-5 f = 2.797-18 x = [1.0, 1.0] @benchmark ofNelderMid(fit = [0., 0.]) BenchmarkTools.Trial: memory estimate: 394.03 KiB allocs estimate: 6632 -------------- minimum time: 717.221 μs (0.00% GC) median time: 769.325 μs (0.00% GC) mean time: 854.644 μs (5.04% GC) maximum time: 50.429 ms (98.01% GC) -------------- samples: 5826 evals/sample: 1

现在有更多理由返回学习套餐

您可以选择使用的方法：

 optimize(f, x0, LBFGS()) Results of Optimization Algorithm * Algorithm: L-BFGS * Starting Point: [0.0,0.0] * Minimizer: [0.9999999926662504,0.9999999853325008] * Minimum: 5.378388e-17 * Iterations: 24 * Convergence: true * |x - x'| ≤ 0.0e+00: false |x - x'| = 4.54e-11 * |f(x) - f(x')| ≤ 0.0e+00 |f(x)|: false |f(x) - f(x')| = 5.30e-03 |f(x)| * |g(x)| ≤ 1.0e-08: true |g(x)| = 9.88e-14 * Stopped by an increasing objective: false * Reached Maximum Number of Iterations: false * Objective Calls: 67 * Gradient Calls: 67

并获取详细的文档和参考

 ?LBFGS()

您可以设置Jacobian和Hessian函数

 function g!(G, x) G[1] = -2.0 * (1.0 - x[1]) - 400.0 * (x[2] - x[1]^2) * x[1] G[2] = 200.0 * (x[2] - x[1]^2) end function h!(H, x) H[1, 1] = 2.0 - 400.0 * x[2] + 1200.0 * x[1]^2 H[1, 2] = -400.0 * x[1] H[2, 1] = -400.0 * x[1] H[2, 2] = 200.0 end optimize(f, g!, h!, x0) Results of Optimization Algorithm * Algorithm: Newtons Method * Starting Point: [0.0,0.0] * Minimizer: [0.9999999999999994,0.9999999999999989] * Minimum: 3.081488e-31 * Iterations: 14 * Convergence: true * |x - x'| ≤ 0.0e+00: false |x - x'| = 3.06e-09 * |f(x) - f(x')| ≤ 0.0e+00 |f(x)|: false |f(x) - f(x')| = 3.03e+13 |f(x)| * |g(x)| ≤ 1.0e-08: true |g(x)| = 1.11e-15 * Stopped by an increasing objective: false * Reached Maximum Number of Iterations: false * Objective Calls: 44 * Gradient Calls: 44 * Hessian Calls: 14

如您所见，他自动计算出牛顿法。因此，您可以设置搜索区域并使用梯度下降：

 lower = [1.25, -2.1] upper = [Inf, Inf] initial_x = [2.0, 2.0] inner_optimizer = GradientDescent() results = optimize(f, g!, lower, upper, initial_x, Fminbox(inner_optimizer)) Results of Optimization Algorithm * Algorithm: Fminbox with Gradient Descent * Starting Point: [2.0,2.0] * Minimizer: [1.2500000000000002,1.5625000000000004] * Minimum: 6.250000e-02 * Iterations: 8 * Convergence: true * |x - x'| ≤ 0.0e+00: true |x - x'| = 0.00e+00 * |f(x) - f(x')| ≤ 0.0e+00 |f(x)|: true |f(x) - f(x')| = 0.00e+00 |f(x)| * |g(x)| ≤ 1.0e-08: false |g(x)| = 5.00e-01 * Stopped by an increasing objective: false * Reached Maximum Number of Iterations: false * Objective Calls: 84382 * Gradient Calls: 84382

好吧，或者我不知道，假设您想解决方程式

 f_univariate(x) = 2x^2+3x+1 optimize(f_univariate, -2.0, 1.0) Results of Optimization Algorithm * Algorithm: Brents Method * Search Interval: [-2.000000, 1.000000] * Minimizer: -7.500000e-01 * Minimum: -1.250000e-01 * Iterations: 7 * Convergence: max(|x - x_upper|, |x - x_lower|) <= 2*(1.5e-08*|x|+2.2e-16): true * Objective Function Calls: 8

他选了你布伦特法。
或拥有实验数据，您需要优化模型系数

（ ， ， ） （ ） （ ）

$F（p_1，p_2，x）= p_1 \ cos（p_2x）+ p_2 \ sin（p_1x）$

，

$p_1 = 1，p_2 = 0.2$

 F(p, x) = p[1]*cos(p[2]*x) + p[2]*sin(p[1]*x) model(p) = sum( [ (F(p, xdata[i]) - ydata[i])^2 for i = 1:length(xdata)] ) xdata = [-2,-1.64,-1.33,-0.7,0,0.45,1.2,1.64,2.32,2.9] ydata = [0.699369,0.700462,0.695354,1.03905,1.97389,2.41143,1.91091,0.919576,-0.730975,-1.42001] res2 = optimize(model, [1.0, 0.2]) Results of Optimization Algorithm * Algorithm: Nelder-Mead * Starting Point: [1.0,0.2] * Minimizer: [1.8818299027162517,0.7002244825046421] * Minimum: 5.381270e-02 * Iterations: 34 * Convergence: true * √(Σ(yᵢ-ȳ)²)/n < 1.0e-08: true * Reached Maximum Number of Iterations: false * Objective Calls: 71

 P = Optim.minimizer(res2) Y = [ F(P, x) for x in xdata] using Plots plotly() plot(xdata, ydata) plot!(xdata, Y)

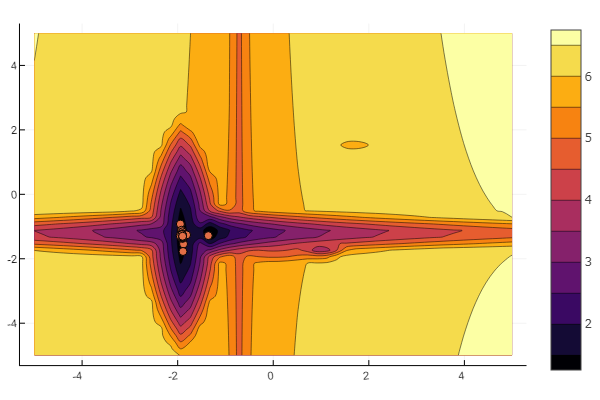
红利创建测试功能

这个想法在哈布罗夫的文章中使用。您可以自己配置每个本地最小值：

 """ https://habr.com/ru/post/349660/ :param n:   :param a:    ,   ,    /      :param c:    :param p:       :param b:    :return:  ,       ,          """ function feldbaum(x; n=5, a=[3 2; 4 3; 2 1; 4 5; .5 .5], c=[-1 2; 2 1; -3 2; -2 -2; 1.5 -2], p=[9 6; 1 1; 1.5 1.4; 1.2 1.3; 0.5 0.5], b=[0 1 3.2 2 4.6]) l = zeros(n) for i = 1:n res = 0 for j = 1:size(x,1) res += a[i,j] * abs(x[j] - c[i,j]) ^ p[i,j] end res += b[i] l[i] = res end minimum(l) end

您可以将一切交给万能的意志

 n=10 m = 2 a = rand(0:0.1:6, n, m) c = rand(-2:0.1:2, n, m) p = rand(0:0.1:2, n, m) b = rand(0:0.1:8, n, m) function feldbaum(x) l = zeros(n) for i = 1:n res = 0 for j = 1:m res += a[i,j] * abs(x[j] - c[i,j]) ^ p[i,j] end res += b[i] l[i] = res end minimum(l) end

但是，正如您从开始的图片中看到的那样，具有如此浮雕的大量粒子并没有令人生畏。

应该做到这一点。如您所见，Julia具有相当强大的现代数学环境，可以进行复杂的数值研究而无需屈从于低级编程抽象。这是继续学习该语言的绝佳时机。

祝大家好运！

朱莉娅和优化

参赛作品

黑药

凸面

跳

最佳

红利 创建测试功能

More articles:

红利创建测试功能