💚 🙇🏽 ✴️ 关系编程：痛苦，兴趣和再次痛苦 ⚽️ 👸🏻 🤑

在上一篇文章中，我们详细介绍了我们在“工业编程”领域教给学生的内容。对于那些感兴趣的领域位于更理论领域的人，例如被编程理论研究中使用的新编程范例或抽象数学所吸引的人，还有另一种专业化知识-“编程语言”。

今天，我将谈论我在关系编程领域的研究，这是我在大学里做的，也是语言工具JetBrains Research实验室中的学生研究者。

什么是关系编程？通常，我们运行带有参数的函数并获取结果。在关系情况下，您可以执行相反的操作：固定结果和一个参数，然后获取第二个参数。最主要的是正确编写代码并保持耐心并拥有良好的集群。

关于我自己

我叫Dmitry Rozplokhas，我是圣彼得堡HSE的一年级学生，去年我毕业于学术大学的“编程语言”领域的学士学位课程。从本科三年级开始，我还是JetBrains研究语言工具实验室的研究学生。

关系编程

一般事实

关系编程是在描述参数和结果之间的关系而不是函数时。如果为此增加了语言能力，则可以获得某些好处，例如，可以以相反的方向运行该功能（因此可以恢复参数的可能值）。

通常，这可以用任何逻辑语言完成，但是大约十年前，随着简约纯逻辑语言miniKanren的出现，人们对关系编程产生了兴趣，这使得方便地描述和使用这种关系成为可能。

以下是一些最高级的用例：您可以编写证明检查器并使用它来查找证据（ Near等人，2008 ）或为某种语言创建解释器并使用它来生成测试套件程序（ Byrd等人，2017 ）。

语法和玩具示例

miniKanren是一种小语言；仅使用基本的数学构造来描述关系。这是一种嵌入式语言，其原语是一些外部语言的库，小型miniKanren程序可以用另一种语言在程序内部使用。

适合miniKanren的外语，一大堆。最初有Scheme，我们正在使用Ocaml（ OCanren ）的版本，完整列表可以在minikanren.org上查看。本文中的示例也将放在OCanren上。许多实现都添加了辅助函数，但我们将仅专注于核心语言。

让我们从数据类型开始。按照惯例，它们可以分为两种类型：

常量是来自我们所嵌入语言的一些数据。字符串，数字甚至数组。但是对于基本的miniKanren来说，这都是一个黑匣子，只能检查常量是否相等。
“术语”是几个元素的元组。通常以与Haskell中的数据构造函数相同的方式使用：数据构造函数（字符串）加上零个或多个参数。 OCanren使用OCaml中的常规数据构造函数。

例如，如果我们要使用miniKanren本身中的数组，则必须用类似于功能语言的术语来描述它-作为单连接列表。列表可以是一个空列表（用一个简单术语表示），也可以是列表的第一个元素（“头”）和其余元素（“ tail”）之间的一对。

let emptyList = Nil let list_123 = Cons (1, Cons (2, Cons (3, Nil)))

miniKanren程序是一些变量之间的关系。在启动时，程序以常规形式给出变量的所有可能值。通常，实现可让您限制输出中答案的数量，例如，仅找到第一个答案-在找到所有解决方案后搜索并不总是停止。

您可以编写几个相互定义的关系，甚至可以作为函数递归调用。例如，下面我们代替函数

追 加 （ a ， b ） \to 与

$追加（a，b）→与$ 定义关系

a p p e n d o （ a ， b ， c ）

$appendo（a，b，c）$ ：清单

c

$c$ 是列表的串联

一

$一$ 和

b

$b$ 。通常，返回关系的函数以“ o”结尾，以将它们与普通函数区分开。

关系写为关于其参数的某种陈述。我们有四个基本操作 ：

两个术语的统一或相等（===），术语可以包含变量。例如，您可以编写关系“列表由一个元素组成 “：
```
 let isSingletono xl = l === Cons (x, Nil) 
```
连词（逻辑“与”）和析取词（逻辑“或”）-与普通逻辑一样。 OCanren称为&&&和|||。但是在MiniKanren中基本上没有逻辑上的否认。
添加新变量。在逻辑上，它是存在的量词。例如，要检查列表的非空性，您需要检查列表是否由头和尾组成。它们不是关系的参数，因此您需要创建新变量：
```
 let nonEmptyo l = fresh (ht) (l === Cons (h, t)) 
```

关系可以递归调用。例如，您需要定义关系

x

$x$ 位于清单上。” 我们将通过分析琐碎的案例来解决此问题，就像在函数式语言中一样：

或列表的开头是 $x$
要么 $x$ 躺在尾巴

 let membero lx = fresh (ht) ( (l === Cons (h, t)) &&& (x === h ||| membero tx) )

语言的基本版本基于这四个操作。还有一些扩展允许您使用其他操作。其中最有用的是用于设置两个项（= / =）不等式的不等式约束。

尽管极简，miniKanren是一种颇具表现力的语言。例如，查看两个列表的关系串联。两个自变量的功能变成三元关系“

a b

$ab$ 是列表的串联

一

$一$ 和

b

$b$ ”。

 let appendo ab ab = (a === Nil &&& ab === b) ||| (fresh (ht tb) (*  :  fresh   &&& *) (a = Cons (h, t)) (appendo tb tb) (ab === Cons (h, tb)))

该解决方案在结构上与我们用功能语言编写的方式没有什么不同。我们分析由一个子句组合的两种情况：

如果第一个列表为空，则第二个列表和串联结果相等。
如果第一个列表不为空，则将其解析为头部和尾部，并使用关系的递归调用构造结果。

我们可以请求此关系，固定第一个和第二个参数-我们得到列表的串联：

 run 1 (λ q -> appendo (Cons (1, Cons (2, Nil))) (Cons (3, Cons (4, Nil))) q)

⇒

 q = Cons (1, Cons (2, Cons (3, Cons (4, Nil))))

我们可以修复最后一个参数-我们将该列表的所有分区分成两个。

 run 4 (λ qr -> appendo qr (Cons (1, Cons (2, Cons (3, Nil)))))

⇒

 q = Nil, r = Cons (1, Cons (2, Cons (3, Nil))) | q = Cons (1, Nil), r = Cons (2, Cons (3, Nil)) | q = Cons (1, Cons (2, Nil)), r = Cons (3, Nil) | q = Cons (1, Cons (2, Cons (3, Nil))), r = Nil

您还可以做其他事情。一个稍微非标准的示例，其中仅修复了部分参数：

 run 1 (λ qr -> appendo (Cons (1, Cons (q, Nil))) r (Cons (1, Cons (2, Cons (3, Cons (4, Nil))))))

⇒

 q = 2, r = Cons (3, Cons (4, Nil))

如何运作

从理论的角度来看，这里没有什么令人印象深刻的：您总是可以开始为所有参数搜索所有可能的选项，检查每个集合是否按照我们希望的方式针对给定的函数/关系运行（请参阅“大英博物馆算法” ）。令人感兴趣的事实是，此处的搜索（换句话说，对解决方案的搜索）仅使用所描述关系的结构，因此在实践中它可能相对有效。

搜索与累积有关当前状态下各种变量的信息有关。我们要么对每个变量一无所知，要么知道它是如何用术语，值和其他变量表示的。例如：

b = Cons (x, y)
c = Cons (10, z)
x = ?
y = ?
z = ?

通过统一，我们考虑了两个信息，并考虑了这些信息，如果两个条件不能统一，则更新状态或终止搜索。例如，完成统一b = c，我们得到新的信息：x = 10，y = z。但是统一b = Nil会引起矛盾。

我们依次搜索合相（以便积累信息），然后我们将搜索分成两个平行的分支，并在其中交替进行，这就是所谓的交错搜索。由于这种交替，搜索完成了-在有限的时间后将找到每个合适的解决方案。例如，在Prolog语言中并非如此。它的作用类似于深度爬网（可以挂在无限分支上），而交错搜索本质上是一个棘手的宽爬网修改。

现在，让我们看看上一节中的第一个查询是如何工作的。由于appendo具有递归调用，因此我们将在变量中添加索引以区分它们。下图显示了枚举树。箭头指示信息传播的方向（递归返回除外）。在析取之间，信息不分布，而在连接词之间，则从左至右分布。

我们从外部调用appendo开始。分离的左分支因争议而死亡：列表 $一$ 不为空。
在右分支中，引入了辅助变量，这些辅助变量随后用于“解析”列表 $a_1$ 在头和尾巴上。
此后，对于a = [2]，b = [3，4]，ab =？进行附录递归调用，在其中发生类似的操作。
但是在第三个对appendo的调用中，我们已经有a = []，b = [3,4]，ab =？，然后左析取运算就起作用了，之后我们得到信息ab = b。但是在正确的分支中存在矛盾。
现在我们可以写出所有可用的信息，并通过替换变量的值来恢复答案：

a_1 = [1, 2] b_1 = [3, 4] ab_1 = Cons h_1 tb_1 h_1 = 1 a_2 = t_1 = [2] b_2 = b_1 = [3, 4] ab_2 = tb_1 = Cons h_2 tb_2 h_2 = 2 a_3 = t_2 = Nil b_3 = b_2 = b_1 = [3, 4] ab_3 = tb_2 = b_3 = [3, 4]
因此 $ab_1$ = Cons（1，Cons（2，[3，4]））= [1,2,3,4]，视需要而定。

我在大学里做什么

一切都变慢

一如既往：他们向您保证一切都将是超级声明性的，但实际上，您需要适应语言并以特殊方式编写所有内容（请记住如何执行所有内容），以便至少可以工作，除了最简单的示例。这真令人失望。

miniKanren新手程序员面临的第一个问题是，它很大程度上取决于描述程序中条件（合词）的顺序。只需一个命令，一切就可以了，但是两个联结被交换了，一切开始非常缓慢，或者根本没有完成。这是意外的。

即使在带有附录的示例中，向相反方向启动（将列表拆分成两部分）也不会结束，除非您明确指定所需的答案数（然后搜索将在找到所需的数字后结束）。

假设我们将原始变量固定如下：a = ?、 B = ?、 Ab = [1、2、3]（请参见下图）在第二个分支中，在递归调用期间将不会以任何方式使用此信息（变量ab和对b的限制）。

h_{1}

$h_1$ 和

t b_{1}

$tb_1$ 仅在此呼叫之后出现）。因此，在第一个递归调用中，其所有参数都是自由变量。此调用将从两个列表及其连接中生成所有类型的三元组（并且这一代将永远不会结束），然后从中选择第三个元素正是我们需要的元素。

一切都没有乍看之下那么糟糕，因为我们将在大型团体中对这些三元组进行分类。从函数的角度来看，具有相同长度但元素不同的列表没有区别，因此它们将落入一种解决方案中-将有自由变量代替元素。尽管如此，尽管我们只需要一个列表长度，但是我们知道哪个列表长度，我们仍将对所有可能的列表长度进行排序。这是搜索中信息的非常不合理的使用（不使用）。

这个特定的示例很容易修复：您只需要将递归调用移到末尾，一切就可以正常进行。在递归调用之前，将与变量ab进行统一，并且将从给定列表的末尾进行递归调用（作为常规递归函数）。最后定义为递归调用的此定义将在所有方向上都很好地工作：对于递归调用，我们设法积累了有关参数的所有可能信息。

但是，在任何稍微复杂的示例中，当存在多个有意义的调用时，就不会有一个一切都会好起来的特定顺序。最简单的示例：使用串联扩展列表。我们修复了第一个参数-我们需要此特定顺序，我们修复了第二个参数-我们需要交换调用。否则，将搜索很长时间，并且搜索不会结束。

 reverso x xr = (x === Nil &&& xr == Nil) ||| (fresh (ht tr) (x === Cons (h, t)) (reverso t tr) (appendo tr (Cons (h, Nil)) xr))

这是因为交错搜索过程按顺序合并，尽管有人尝试过，但没有人想出如何做不同的方法而不会失去可接受的效率。当然，总有一天会找到所有解决方案，但是以错误的顺序，它们的搜索时间会不切实际，以至于没有实际意义。

有一些编写程序的技术可以避免此问题。但是其中许多需要特殊的技能和想象力才能使用，结果是程序非常庞大。一个例子是术语大小限制技术，以及在乘法的帮助下使用余数进行二进制除法的定义。而不是愚蠢地写一个数学定义

 divo nmqr = (fresh (mq) (multo mq mq) (pluso mq rn) (lto rm))

我必须写一个20行的递归定义+一个庞大的辅助函数，这是不现实的（我仍然不明白那里正在做什么）。可以在Will Bird的论文 “纯二进制算术”部分中找到它。

鉴于上述情况，我想对搜索进行某种修改，以使简单自然的程序也可以工作。

优化

我们注意到，当一切都不好时，除非您明确指出答案数量并中断答案，否则搜索不会结束。因此，他们决定与搜索的不完全精确地战斗-具体化比“长期有效”要容易得多。总的来说，当然，我只是想加快搜索速度，但是要正规化起来要困难得多，因此我们从一个不太雄心勃勃的任务开始。

在大多数情况下，当搜索分散时，就会出现易于跟踪的情况。如果以递归方式调用函数，并且在递归调用中，参数相同或较少特定，则在递归调用中会再次生成另一个此类子任务，并发生无限递归。形式上听起来像是这样：有一个替代，将其应用于新参数，我们得到旧参数。例如，在下图中，递归调用是原始调用的概括：您可以替换为

c_{2}

$c_2$ = [x，3]，

d_{2}

$d_2$ = x并获得原始呼叫。

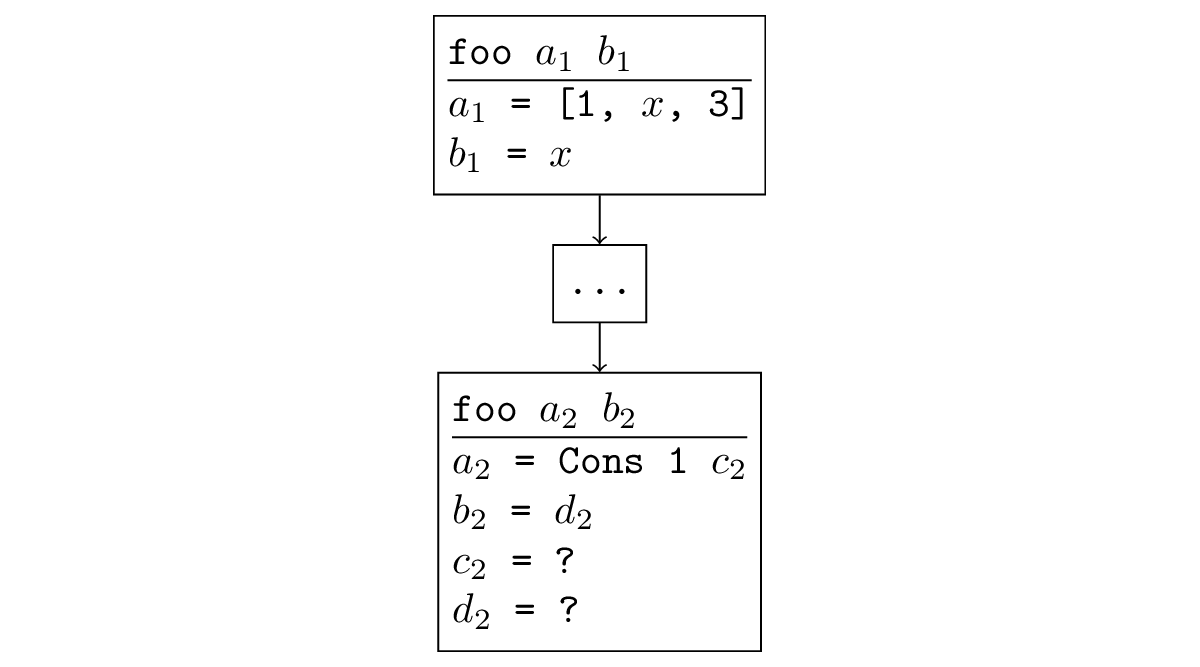
可以追溯到，在我们已经遇到的分歧示例中也出现了这种情况。正如我之前所写的，当您沿相反方向运行appendo时，将使用自由变量而不是所有变量进行递归调用，这当然不如固定了第三个参数的原始调用具体。

如果我们用x =进行反向操作？并且xr = [1，2，3]，可以看出第一次递归调用将再次使用两个自由变量发生，因此新的自变量显然可以再次传递给先前的自变量。

 reverso x x_r  (* x = ?, x_r = [1, 2, 3] *) fresh (ht t_r) (x === Cons (h, t)) (* x_r = [1, 2, 3] = Cons 1 (Cons 2 (Cons 3 Nil))) x = Cons (h, t) *) (reverso t t_r) (* :   t=x, t_r=[1,2,3],    *)

使用此标准，我们可以检测程序执行过程中的差异，了解此顺序对所有方面都是不利的，然后动态地将其更改为另一个顺序。因此，理想情况下，将为每个呼叫选择正确的顺序。
您可以天真地做到这一点：如果在合词中发现分歧，那么我们将敲定他已经找到的所有答案，并将其执行推迟到以后，“跳过”下一个合词。然后，也许，当我们继续执行它时，将已经知道更多信息，并且不会出现分歧。在我们的示例中，这将导致所需的交换合路。

有一些天真的方法可以（例如）不丢失已经完成的工作，推迟性能。已经是改变顺序的最愚蠢的变体，在我们所知道的连词具有非可交换性的所有简单示例中，分歧已经消失了，包括：

对数字列表进行排序（也是列表的所有排列的生成），
Peano算术和二进制算术，
给定大小的二叉树的生成。

这对我们来说是一个意外的惊喜。除了差异之外，优化还可以防止程序变慢。下图显示了两个不同顺序结合在一起的程序的执行时间（相对而言，最好的是其中之一，而坏的是其中之一）。它是在配置了Intel Core i7 CPU M 620、2.67GHz x 4、8GB RAM和Ubuntu 16.04操作系统的计算机上启动的。

当订单已经是最佳订单时 （我们手动选择），优化会稍微减慢执行速度，但这并不关键

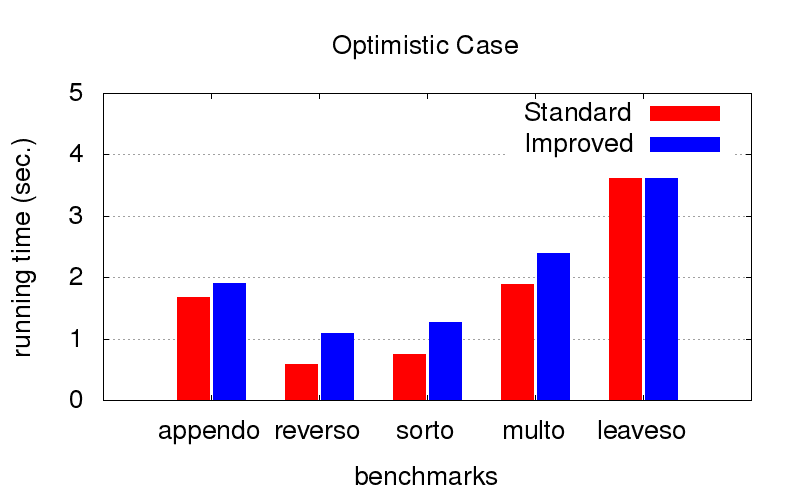
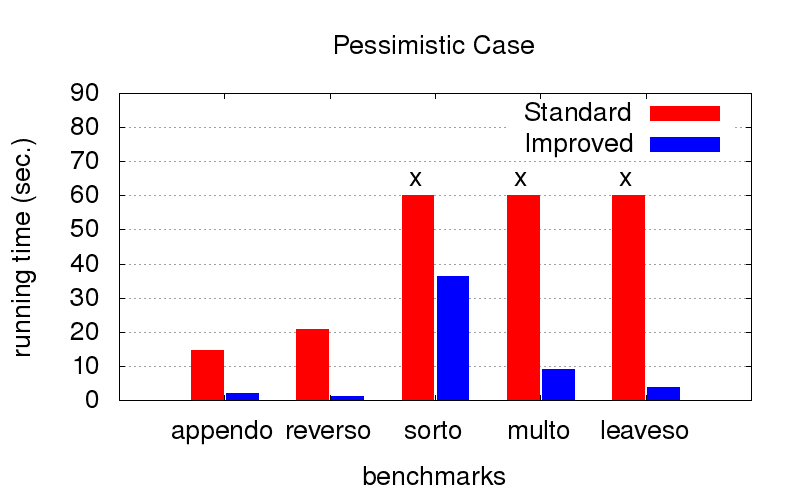
但是，当顺序不是最佳时 （例如，仅适用于相反方向的发射），通过优化，结果会更快。十字架意味着我们迫不及待地想要结束，它的工作时间更长

怎么不破

所有这些纯粹是基于直觉，我们想严格证明这一点。毕竟理论。

为了证明某些东西，我们需要语言的形式语义。我们描述了miniKanren的操作语义。这是真实语言实现的简化和数学化版本。它使用的版本非常有限（因此易于使用），您只能在其中指定程序的最终执行（搜索应该是最终的）。但是出于我们的目的，这正是需要的。

为了证明这一标准，首先制定了引理：从更一般的状态执行程序将工作更长的时间。形式上：语义上的输出树高度很大。这可以通过归纳证明，但是必须非常仔细地概括该陈述，否则归纳假设将不够强大。从这个引理可以得出结论，如果某个标准在程序执行期间起作用，则输出树将具有其自己的更大或相等高度的子树。这给出了一个矛盾，因为对于归纳给定的语义，所有树都是有限的。这意味着按照我们的语义，该程序的执行是无法表达的，这意味着该程序的搜索不会结束。

提议的方法是保守的：仅当我们确信一切都已经完全坏了并且不可能做得更糟时，我们才会更改某些内容，因此我们不会在程序完成方面破坏任何内容。

主要证明包含很多细节，因此我们希望通过写Coq来正式验证它。但是，从技术上讲，这非常困难，因此我们降低了热情，仅在治安部门认真从事自动验证。

过帐

在工作的中间，我们在ICFP-2017学生研究竞赛的海报会议上介绍了这项研究。在这里，我们遇到了该语言的创建者-Will Bird和Daniel Friedman-他们说这很有意义，我们需要更详细地研究它。顺便说一下，Will通常是我们JetBrains Research实验室的朋友。我们对miniKanren的所有研究都始于2015年Will在圣彼得堡举办的关系编程暑期班时。

一年后，我们将我们的工作大致化为完整形式，并在《声明式编程的原则和实践2018》中介绍了该文章。

我在研究生院做什么

我们希望继续从事miniKanren的形式语义和对其所有属性的严格证明。在文献中，通常简单地假设并使用示例来演示属性（通常不很明显），但是没有人提供任何证据。例如，有关关系编程的主要书籍是一个问题和答案的列表，每个问题和答案都专用于一段特定的代码。即使声明了交错搜索的完整性（这也是miniKanren优于标准Prolog的最重要优势之一），也无法找到严格的措词。我们决定，您不能那样生活，在得到威尔的祝福后，我们开始工作。

让我提醒您，我们在上一阶段开发的语义有一个很大的局限性：仅描述了具有有限搜索的程序。在miniKanren中，正在运行的程序也很有趣，因为它们可以列出无数个答案。因此，我们需要更酷的语义。

定义编程语言语义的标准方法有很多，我们只需要选择其中一种并将其适应特定情况即可。我们将语义描述为标记的转换系统-搜索过程中的一组可能状态以及这些状态之间的转换，其中一些状态已标记，这意味着在搜索的这一阶段，找到了另一个答案。因此，特定程序的执行由此类转换的顺序确定。这些序列可以是有限的（进入终端状态）或无限，描述同时终止和未完成程序。为了在数学上完全指定这样的对象，需要使用一个共归定义。

上面描述的语义是可操作的 -它反映了搜索的实际实现。除此之外，我们还使用了指称语义，它使一些数学对象与语言程序和构造中的自然程序相关联（例如，程序中的关系被视为一组术语上的关系，连接是关系的交集等）。定义此类语义的标准方法称为最小的Erbran模型，而对于miniKanren而言，它已在较早之前完成（也在我们的实验室中完成）。

此后，语言的搜索完整性以及正确性可以表述为这两种语义的对等关系-特定程序中答案集的重合。我们设法证明了这一点。有趣的是（有点难过），我们没有使用多个嵌套的归纳参数不同的归纳法。
作为推论，我们还获得了一些有用的语言转换的正确性（根据获得的解集）：如果该转换显然不改变相应的数学对象，例如重新排列或使用分配性连词或析取词，则搜索结果不会改变。

现在，我们要使用语义来证明语言的其他有用属性，例如，其他语言构造的完整性/差异性或正确性的标准。

我们还对使用Coq进行形式化的严格描述进行了更详细的介绍。在克服了许多不同的困难并付出了很多努力之后，我们现在能够设置语言的操作语义并提供一些证据，在纸上的形式为“很明显。Qed。” 我们不会对自己失去信心。

关系编程：痛苦，兴趣和再次痛苦