👐🏻 👩‍🎨 👨‍🚒 Wolfensteiny 3D-反向工程251字节的JavaScript 👩🏾 ⛽️ 🧒🏿

在编写代码时，除了程序本身的逻辑外，许多人不会考虑其他事情。很少有人考虑从内存中逐步优化代码。但是只有少数几个达到了最后的水平-将程序压缩到创纪录的小尺寸。

例如，查看仅251个字节的 JavaScript的结果：

好吧，让我们弄清楚它是如何工作的！

它是哪里来的？

这段代码以及我在本文中介绍的很多内容都位于JavaScript开发人员Mathieu'p01'Henri的网站p01.org上，它不仅经常涉及将代码压缩为不可能的大小。本文的原始资料在这里。

因此，在您之前只有251个字节的源代码。

<body onload=E=c.getContext("2d"),setInterval(F="t+=.2,Q=Math.cos;c.height=300;for(x=h;x--;)for(y=h;y--;E.fillRect(x*4,y*4,bd?4:D/2,D/2))for(D=0;'.'<F[D*y/hD/2|0?1:(d=t+D*Q(T=x/h-.5+Q(t)/8)&7)|(3.5+D*Q(T-8))<<3]&&D<8;b=d)D+=.1",t=h=75)><canvas id=c>

显然，没有什么是清楚的。

使代码可读

首先，为了方便起见，我将所有JavaScript代码放在一个单独的标签中。

可以看出，变量E ， h ， Q ， F和其他是常量，可以用其值/对象本身替换，也可以更改名称。

 var context = c.getContext("2d") var F="t+=.2,Q=Math.cos;c.height=300;for(x=h;x--;)for(y=h;y--;E.fillRect(x*4,y*4,bd?4:D/2,D/2))for(D=0;'.'<F[D*y/hD/2|0?1:(d=t+D*Q(T=x/h-.5+Q(t)/8)&7)|(3.5+D*Q(T-8))<<3]&&D<8;b=d)D+=.1" var t = 75 var size = 75 function render(){ t += 0.2; c.height=300; for(let x = size; x--;) for(let y = size; y--; context.fillRect(x * 4,y * 4,b - d? 4 : D / 2, D / 2)) for(var D = 0; '.' < F[D * y / size - D / 2 | 0 ? 1 : (d = t + D * Math.cos(T = x / size - 0.5 + Math.cos(t) / 8) & 7) | (3.5 + D * Math.cos(T - 8)) << 3] && D < 8; b = d) D += 0.1 } setInterval(render, 75);

在这里，字符串中的代码已经被提取到函数中，并且字符串本身未受影响，将来我们将需要它。

现在将两个外部循环转换为while 。

 function render(){ t += 0.2; c.height=300; let x = size; while(x > 0){ let y = size; while(y > 0){ for(var D = 0; '.' < F[D * y / size - D / 2 | 0 ? 1 : (d = t + D * Math.cos(T = x / size - 0.5 + Math.cos(t) / 8) & 7) | (3.5 + D * Math.cos(T - 8)) << 3] && D < 8; b = d) D += 0.1 context.fillRect(x * 4,y * 4,b - d? 4 : D / 2, D / 2); y--; } x--; } }

我们怎么看呢？

让我们了解为什么我们会看到它。如果再次查看图片，您将会了解很多。

可点击的图片

这是我们看到的：

主体越远，它越暗
遇到的障碍物的倾斜部分以不同的线条（而不是点）淹没。

在代码中，图形是这样反映的：

 // ,  ,       //   ||     // | | || | | // ↓ ↓ ↓↓ ↓ ↓ context.fillRect(x * 4,y * 4,b - d? 4 : D / 2, D / 2);

为什么在大量黑点中看到体积物体？毕竟，我们只能满足于不同深浅的黑色-黑点的大小（我们无法更改颜色， E.fillStyle太长！）。实际上，它的工作原理很简单，因为在二维图片中，我们的眼睛主要依赖于光线的阴影和亮度。

想象一下自己手中只有一个手电筒的黑暗走廊。您在自己面前发光，看到有些物体更近，更亮（手电筒发光，障碍物很亮，没有阴影），而另一些物体则更远，更暗（光散在，微弱，我们看到了黑暗-我们感受到了距离）。因此，在这里-对象越远（ D越大），尺寸越大，我们在屏幕上绘制一个黑色正方形。
但是，我们如何知道什么需要亮而不是什么呢？

计数像素

现在让我们来处理这个怪物：

 for(var D = 0; '.' < F[D * y / size - D / 2 | 0 ? 1 : (d = t + D * Math.cos(T = x / size - 0.5 + Math.cos(t) / 8) & 7) | (3.5 + D * Math.cos(T - 8)) << 3] && D < 8; b = d) D += 0.1

这样啊所有这些表达式都是固定步长的光线扩散算法 ，可让您找到光束与块的交点。对于屏幕的每个像素，我们发射光束，并以固定的步长0.1跟随光束，一旦遇到障碍，就完成算法并在屏幕上绘制一个像素，知道到障碍的距离。

让我们开始部分阅读此代码。

条件D * y / size - D / 2 | 0 D * y / size - D / 2 | 0可以表示为

D * （ f r a c y s i z e - f r a c 12 ） = D * （ f r a c y - s i z e / 2 s i z e ） < 1

$D *（\ frac {y} {size}-\ frac {1} {2}）= D *（\ frac {y-size / 2} {size}）<1$ ，则括号中的表达式将显示距屏幕中心的“偏差” y （以屏幕的分数为单位）。因此，我们试图了解光束是否在地板和天花板之间。因此，如果我们触摸地板（或天花板），我们将进一步退出循环，进行绘制并绘制一个像素。
如果我们不触摸，则继续进行计算：我们搜索光束的当前坐标。

 var T = x / size - .5 + Math.cos(t) / 8; // Math.cos(t)   //    var xcoord = t + depth * Math.cos(T); var ycoord = 3.5 + depth * Math.cos(T - 8); //

为什么是cos（T-8）？

所以事实证明

c o s （ x - 8 ） \近 似 正 弦 （ x ）

$cos（x-8）\近似正弦（x）$ 精度为0.15弧度。都是因为

f r a c 5 p i 2 \约 8.15 \约 8

$\ frac {5 \ pi} {2} \约8.15 \约8$

然后

c o s （ a l p h a - 8 ） \大 约 c o s （ a l p h a - f r a c 5 p i 2 ） = c o s （ a l p h a - f r a c p i 2 ） = s i n （ a l p h a ）

$cos（\ alpha-8）\大约cos（\ alpha- \ frac {5 \ pi} {2}）= cos（\ alpha-\ frac {\ pi} {2}）= sin（\ alpha）$

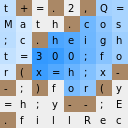
值得一提的是，一般来说，如何检查空间点是否存在障碍。该卡本身取自源代码（ F ），看起来像这样：

 t+=.2,Q= ----> ░█░█░█░░ Math.cos ----> ░░░░█░░░ ;c.heigh ----> ░░█░░░░░   - t=300;fo ----> ░░░░░░░░ <----  , r(x=h;x- ----> ░█░░░░░█     -;)for(y ----> █░█░░░█░ =h;y--;E ----> ░░░░██░░ .fillRec ----> █░░░░░░░

因此看起来好像在运动中，此处指示了摄像机的视野。

那些符号代码小于点代码"."标记为黑暗"." -即字符!"#$%&'()*+,-.现在，我们对光束的坐标进行四舍五入，并尝试找出给定的“坐标”字母是否为“暗（障碍）”（进一步使光束飞）。

由于索引是1，坐标是2，因此我们使用技巧：

 var boxIndex = xcoord & 7 | ycoord << 3;

结果，我们得到一个反映块编号的数字（井或空隙）。

让我们回到代码。现在他看起来不错。

代码有点胖

 function render(){ t += 0.2; c.height=300; let x = size; while(x > 0){ let y = size; while(y > 0){ var depth = 0 while(depth < 8){ depth += 0.1 var T = x / size - .5 + Math.cos(t) / 8; //   var isFloorOrCeiling = depth * y / size - depth / 2 | 0; //      ? if(isFloorOrCeiling) break; var xcoord = t + depth * Math.cos(T) & 7; var ycoord = 3.5 + depth * Math.sin(T); // cos - 8 -> sin boxIndex = xcoord | ycoord << 3; //     , //    if ('.' >= F[boxIndex]) break; b = xcoord; //  ?  ! } context.fillRect(x * 4, y * 4, b - xcoord ? 4 : depth / 2, depth / 2) y--; } x--; } }

回到图纸

为什么我们需要所有这些？现在，执行此算法后，我们知道了到对象的距离，并可以绘制它。但是一个问题仍然没有答案：如何区分天花板和独立的单元？毕竟，到天花板和块的距离是相同的数字！实际上，我们已经回答了这个问题。

 // ,  ,      // || // ↓↓ context.fillRect(x * 4, y * 4, b - xcoord ? 4 : depth / 2, depth / 2);

代码中有一个条件与变量b ，并且会影响“大黑色像素”的宽度： b - xcoord ? 4 : depth / 2 b - xcoord ? 4 : depth / 2 。让我们删除这种情况，看看没有这种情况会发生什么：

砖块和天花板之间没有边界！ （可点击）

条件b - xcoord当坐标更改为0时， b - xcoord将为我们提供恒定的宽度。什么时候不会发生这种情况？仅当我们未到达代码中的（2）行时，才会发生这种情况：

 // .... var xcoord = t + depth * Math.cos(T) & 7; // <---    (1) // ... if ('.' >= F[boxIndex]) // <---    (3) break; b = xcoord; // <---     (2) // ....

这意味着，当光束沿几乎垂直于其壁的方向进入不透明块时，即，它落入块的“面”面时，程序在行（3）上更早退出循环。因此，所有砖块都不同于地板和天花板。

因此，这就是这张精美的3D画面的结果，它不仅使您赏心悦目，而且使您思考其工作方式和原因。您可以在此处查看此代码的运行情况（此奇迹开发人员的站点）。

Wolfensteiny 3D-反向工程251字节的JavaScript

使代码可读

我们怎么看呢？

计数像素

回到图纸

More articles: