分形的无理数

本文是我第一篇文章“素数分形”的续篇。

下一篇： 无理数的分形。 第二部分



在上一篇文章中，我们学习了如何使用互质数绘制自相似模式。 在本文中，我将展示数字的分形性质 $$$\ sqrt {2}$ 。
没有前言。 在猫下。

我们将定义术语和符号。 在数学中，以下描述的系统称为台球 。 此外，我们将使用该术语。 矩形台球的尺寸将用 $$$M$ （宽度）和 $$$N$ （高度）。

二元台球

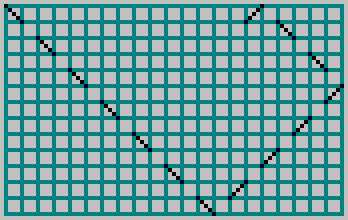
在上一篇文章中，我们制作了一个带有侧面的矩形台球 $$$M$ 和 $$$N$ ，向其中发射了一个球，并在单元格中用虚线标记了轨迹：



为了相互简单 $$$M$ 和 $$$N$ 我们得到的模式：



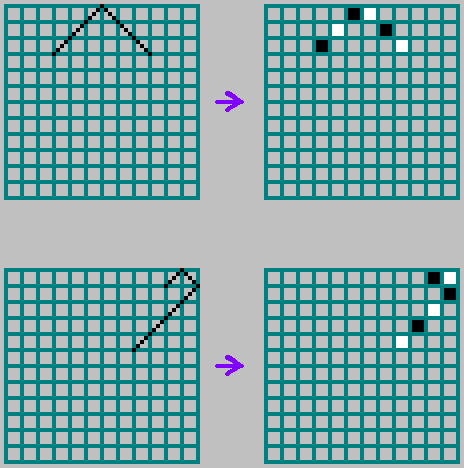
在二进制版本中，我们不用虚线标记轨迹，而是用黑色和白色交替绘制单元格（我们形成一个二进制数组，在对应的单元格中将黑色表示为0，将白色表示为1）：



边界反射规则：



为了相互简单 $$$M$ 和 $$$N$ 轨迹穿过每个像元：




如果双方有一个共同的除数，则球在通过每个像元之前先进入角点：



将这种情况考虑为带边矩形的台球是很方便的 $$$\ frac {M} {GCD}$ 和 $$$\ frac {N} {GCD}$ （GCD是最大的公因数）：



在继续之前，请填写用户Captain1312在其文章中建议的表格（我们将台球的侧面分成GCD）。

$$$（1，0）$ 有点

对于每个台球桌 $$$M$ 和 $$$N$ 用坐标一点 $$$（1，0）$ 。



如果 $$$M$ 是一个分隔线 $$$N$ -再加上一点坐标 $$$（1，0）$ 缺少（ $$$\ frac {M} {GCD} = 1$ ） 在这种情况下，我们将反位与坐标 $$$（0，1）$ 。

填写表格。 原点是左上角。 由 $$$x$ -台球宽度 $$$M$ 由 $$$y$ -身高 $$$N$ 。 对于每个台球，我们都标记了一点 $$$（1，0）$ 或反转位 $$$（0，1）$ （我们将在下面返回此主题）。

二进制序列

为什么当台球宽度倒置时 $$$M = 1$ ？ 为了相互简单 $$$M$ 和 $$$N$ ，球的轨迹穿过每个像元。 在台球的上壁和左壁之间，球每次都经过偶数个孔。





左列中的位是顶行中的反位。 我们不取零位-轨迹从零开始



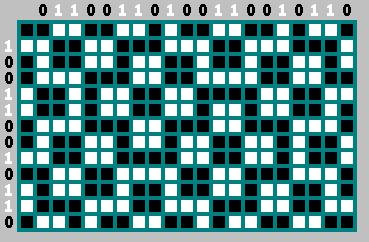
另外，我们可以安全地将第二个比特丢掉该序列（ $$$2_ {n-1}$ -倒位 $$$2_ {n}$ ）：



得到了序列 $$$10100110110$ 台球 $$$（21,13）$ 。 该序列对每个人都是唯一的。 $$$M$ 和 $$$N$ 。

不论高度 $$$N$ 我们没有接受-球总是沿着轨迹移动 $$$2N$ 在顶壁的两次反射之间。 从顶壁开始，移动始终以“ 0”位（黑色单元格）开始，并以“ 1”位（白色单元格）结束：



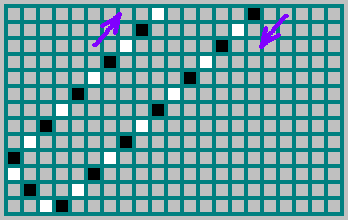
实际上，序列（我们在上面强调了- $$$10100110110$ ）表示球从哪一侧飞入：1-如果球从右壁反射而入，而0-如果球从左壁反射而入。 在图中，如果球向右移动，则球的轨迹标记为黑色；如果球向左移动，则球的轨迹标记为白色：




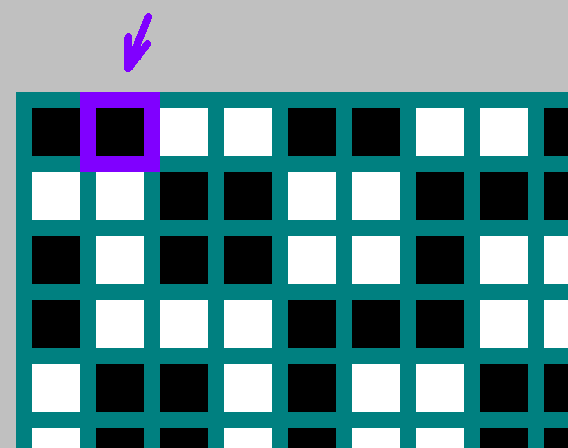
此顺序（ $$$10100110110$ ）包含有关该模式的所有必要信息。 有了它，我们可以恢复原始图案（甚至看起来超出图案的下边界）。 带边的正方形 $$$M$ 。 我们将序列的位排列在球撞击上壁的位置（球的两次相邻接触之间的距离为2个像元）。



如果相应的位= 1-我们开始向左移动，标记通过该单元格的轨迹。 如果位= 0-向右移动。



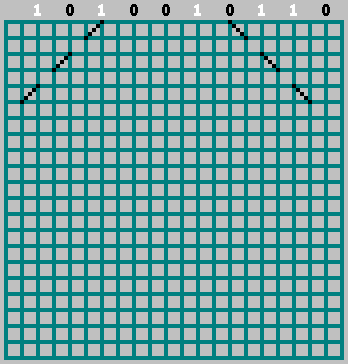
在这种情况下，请不要忘记零位：



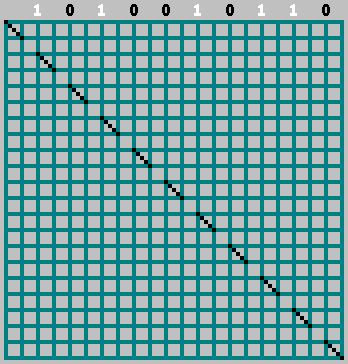
Gif：



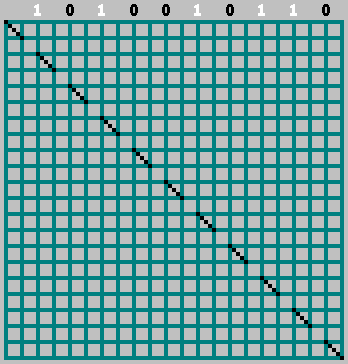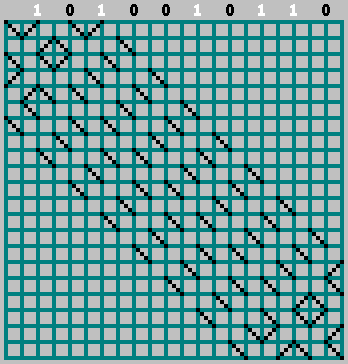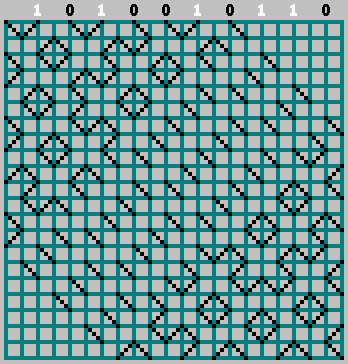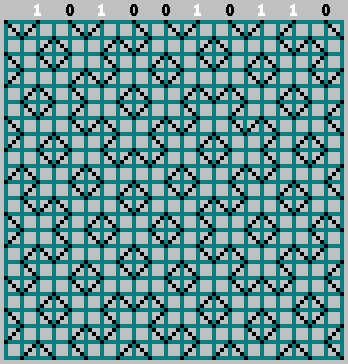
我们得到了原始图案（看上去比下边框稍大一点）：



可视化二进制序列的脚本

我们可以使用除法的其余部分来构建此序列。

一维台球

在数值轴上 $$$X$ 有两点： $$$0$ 和 $$$M$ 。



从一个点移动到另一个点，测量距离 $$$N$ ：



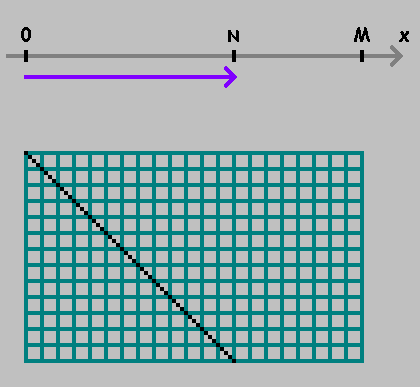
指出了重点。 我们继续测量从该点开始的距离，并保持方向。 如果您已经达到目的 $$$0$ 或 $$$M$ -更改方向：



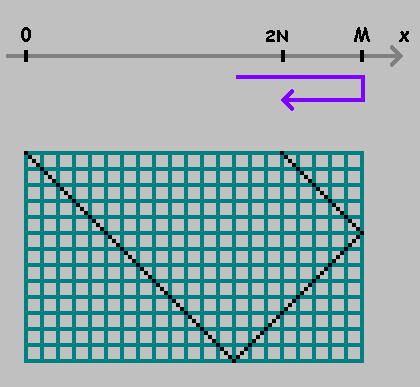
从上图中可以看出，第一个点显示了球与台球底壁接触的位置。 这一点使我们不感兴趣。 我们只会修复点 $$$2kN$ 为 $$$k = 0,1,2，...$ 。

如何标记这些点？ 在轴上转动我们的台球 $$$X$ 。 标记点 $$$0，M，2M，3M，...$ 。 现在到了重点 $$$M$ 我们不会改变运动方向，而是继续前进 $$$200万美$ 。



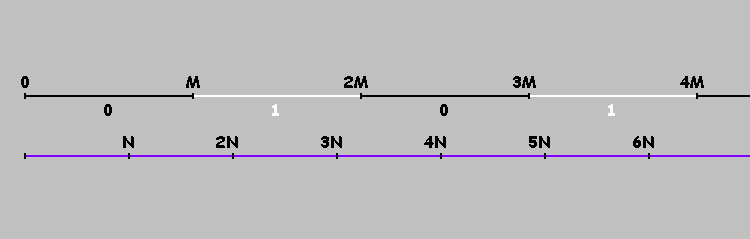
倍数 $$$M$ ，将我们的轴分为多个部分。 我们有条件地用1和0（交替）标记这些段。 在标有零的线段上，球（在矩形台球中）从左向右移动。 在标有单位的线段上-从右到左。 或更简单：如果 $$$Q_k = 0$ 为

$$

$$Q_k = \ lfloor \ frac {2kN} {M} \ rfloor \; （\ textrm {mod} \; 2）; \ quad k = 0,1,2，...$$

（应特别注意该公式。接下来，我们将返回到该公式）

很容易看出，球与台球顶壁的接触点是该部分的其余部分。 $$$2kN$ 在 $$$M$ 。 在这种情况下，我们无法固定球沿相反方向的运动。 我们负责整个部门 $$$2kN$ 在 $$$M$ 如果是偶数-我们考虑除法的其余部分 $$$2kN$ 在 $$$M$ 。 将所得的余数除以2（相邻接触点之间的距离为两个像元）。 得到了数组元素的索引，我们需要用零填充。 其余元素填充有单位（球从右壁向左移动）。

序列长度= $$$\ frac {M} {2}$ 。

function sequence(m,n){ var md=m/2; var array=[]; for(var k=0;k<md;k++) array[k]=1; for(var k=0;k<md;k++) if(Math.floor(2*k*n/m)%2==0) array[((2*k*n)%m)/2]=0; return array; } console.log(sequence(55, 34).join('')); // -> 0101001011010010110101101001 

现在我们可以为任何面的台球建立一个二进制序列 $$$M$ 和 $$$N$ （按自然数）。
一些例子：
144x89（斐波纳契数）：
010100101101001011010110100101101001010010110100101101011010010110100101

169x70（电话号码）：
0101011010100101011010100101011010110101001010110101001010110101001010010101101010010

233x55（奇数斐波那契数 $$$F_n$ 和 $$$F_ {n-3}$ ）：
0100100110110110010011011011001001001101100100100110110010010011011011001001101101100
10010011011001001001101100100100


我们有序列。 您还能如何可视化二进制序列？ 使用Turtle图形 。

龟图形

画一条线。 接下来，我们从序列中交替取出位。 如果bit = 1-相对于上一个段旋转段 $$$60 ^ {\ circ}$ （顺时针）。 如果位= 0-将段旋转 $$$-60 ^ {\ circ}$ 。 下一段的开始是上一段的结束。



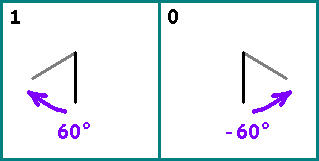
取两个足够大的斐波那契数： $$$F_ {29} = 514229$ 和 $$$F_ {28} = 317811$ 。

建立顺序：
00101101001011010010100101101001011010110100101101001010010110100101 ...（257114个字符加零位）。

我们使用乌龟图形进行可视化。 初始片段的大小为10像素（初始片段位于右下角）：



初始段的大小为5个像素：



初始段的大小为1个像素：



下一个示例是佩尔数字。

$$

$$P_n = \开始{cases} 0，n = 0; \\ 1，n = 1 \\ 2P_ {n-1} + P_ {n-2}，n> 1 \ end {cases}$$

拿 $$$P_ {16} = 470832$ 和 $$$P_ {15} = 195025$ 。

顺序：
0010100101011011010100101011010100101001010110101001010110101000010101101（235415个字符加零位）。

初始段的大小为1个像素：



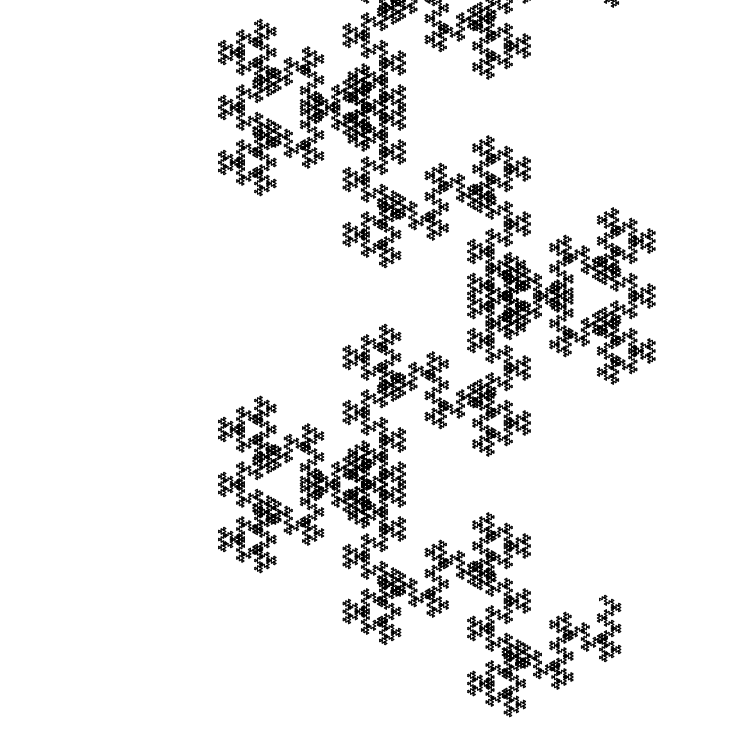
另一个例子是斐波那契奇数 $$$F_n$ 和 $$$F_ {n-3}$ 。
拿 $$$F_ {28} = 317811$ 和 $$$F_ {25} = 75025$ 。
顺序：
0011011001001001111111001001001101101100100110110110010010011011011001001 ...（158905加零位）。
代替角落 $$$60 ^ {\ circ}$ 和 $$$-60 ^ {\ circ}$ 我们将使用角落 $$$90 ^ {\ circ}$ 和 $$$-90 ^ {\ circ}$ 。
初始段的大小为5个像素：



初始段的大小为0.4像素：



该曲线的名称为“ 斐波那契单词分形 ”。 该曲线的Hausdorff尺寸是已知的：

$$

$$D = 3 {\ frac {\ log \ Phi} {\ log（1 + {\ sqrt {2}}）}} = 1,6379; \ quad \ Phi = \ frac {1 + {\ sqrt {5}}} {2}$$

使用Turtle Graphics可视化二进制序列的脚本

问题

是否有可能为台球画出图案，这些台球的侧面是无与伦比的（侧面之一是无理数）？ 这项任务并不简单。 为了解决这个问题，我们将面临许多问题：

1.如果当事方无与伦比-我们不能用大小相同的小室铺台球。
2.如果两边不可估量-球将无限反射，并且永远不会撞到角落。
3.台球中的顺序不是按顺序填充的，而是随机填充的。



前两个问题显然没有解决方案。 但是，如果有一种方法可以按顺序填充序列，那么我们可以从左向右移动序列，以上面使用的方式恢复模式。 从而看到图案在台球的左上角看起来如何，台球的侧面是无与伦比的。

黑魔法

拿台球，其侧面等于斐波纳契数（与其他数字相同，这种技巧可能行不通）。 将球插入其中，并固定接触上壁的球的编号。 用白色填充数字（如果球从右移动到左，则用黑色填充）（如果球从左移动到右）：



白色对应于序列中的一个，黑色对应于零。 现在让我们按顺序排列数字：



我们得到了完全相同的1和0序列。


实际上，在某些情况下，我们不需要进行其余的划分。 对于斐波那契数，检查除法整数部分的奇偶校验就足够了 $$$2kN$ 在 $$$M$ ：

$$

$$Q_k = \ lflo \ frac {2kN} {M} \ rfloor \; （\ textrm {mod} \; 2）; \ quad k = 0,1,2，...$$

在分子中 $$$F_ {n}$ 。 在分母中- $$$F_ {n + 1}$ 。

如您所知：

$$

$$\ lim_ {n \ to \ infty} \ frac {F_n} {F_ {n + 1}} = \ frac {1} {\ Phi}$$

$$$\皮皮$ -黄金分割率。 无理数。 现在我们可以将公式写为：

$$

$$Q_k = \ lfloor \ frac {2k} {\ Phi} \ rfloor \; （\ textrm {mod} \; 2）; \ quad k = 0,1,2，...$$

我们得到一个公式，可以用来按顺序填充台球序列，其宽度等于 $$$\皮皮$ 和高度 $$$1$ 。 序列长度= $$$\ infty$ ，但是我们可以恢复部分图案，依次从左到右移动并查看台球的左上角。 有待弄清楚如何计算 $$$\皮皮$

单位除以黄金分割率可以改写为：

$$

$$\ frac {1} {\ Phi} = \ frac {-1 + {\ sqrt {5}}} {2}$$

我们可以摆脱两个：

$$

$$\ frac {2k} {\ Phi} = \ frac {2k（-1 + {\ sqrt {5}}）} {2} = k \ sqrt {5} -k$$

我们的公式采用以下形式：

$$

$$Q_k = \ lf k \ sqrt {5} -k \ rfloor \; （\ textrm {mod} \; 2）; \ quad k = 0,1,2，...$$

为了清楚起见，我画了一张桌子。 在第三列中，我们丢弃小数部分并保留整个部分。 在第四列中，我们检查整数部分的奇偶校验：



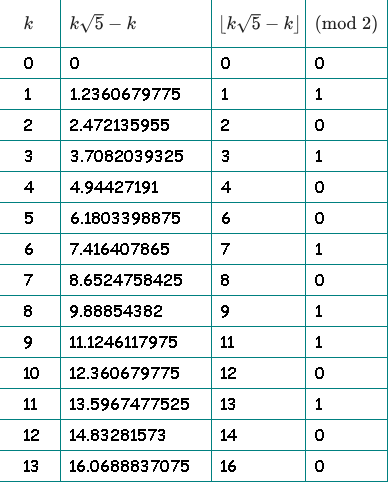
在第四列中，我们得到了以下序列：01010010110100 ...

我们继续计算其余的位 $$$k$ 。 恢复带有侧面的台球图案的一部分 $$$1$ 和 $$$\皮皮$ ：



如果不是每次都带走 $$$k$ -然后，序列中的每一秒都将反转。 我们得到一般公式：

$$

$$Q_k = \ lf k \ sqrt {x} \ rfloor \; （\ textrm {mod} \; 2）; \ quad k = 0,1,2，...$$

是什么使我们无法使用3或2的平方根而不是5的平方根？ 没事

我们构造一个序列 $$$k \ sqrt {3} + k$

 var x=3; var q=[]; for(var k=0;k<256000;k++) q[k]=Math.floor(k*Math.sqrt(x)+k)%2; 

序列的前几位：
00100101101001001011010010110110100101101001001011010010010110100101 ...

我们将使用乌龟图形进行可视化。 90度和-90度的角度。 初始片段大小为5像素：



初始段的大小为0.5像素：



我们构造一个序列 $$$k \ sqrt {2}$

 var x=2; var q=[]; for(var k=0;k<256000;k++) q[k]=Math.floor(k*Math.sqrt(x))%2; 

序列的前几位（ A083035 ）：
01001101100100110010011011001101100100110110011011001001100100110110 ...

90度和-90度的角度。 初始片段大小为5像素：



初始段的大小为0.5像素：





角度为60度和-60度。 初始片段大小为5像素：



可视化脚本

有人可能会怀疑整数部分的奇偶校验 $$$k \ sqrt {2}$ 给出一个分形序列。 我们以第二种方式可视化此序列的一部分：



为了清楚起见，我绘制了所得图案中最长的曲线：



该曲线的名称为“斐波纳契分形”。

如何使用台球获得此序列？ 我们拿台球，其宽度= 1，高度= $$$\ sqrt {2}$ 。 在上下边界处，我们确定球的运动方向。 如果球从左向右移动-写0，如果球从右向左-写1。



两张图：

$$

$$z = \ lfy y \ sqrt {x} \ rfloor \; （\ textrm {mod} \; 2）$$

$$

$$z = \ lfy yx \ sqrt {2} \ rfloor \; （\ textrm {mod} \; 2）$$

您可以按照这种方式继续很长时间-模式具有许多有趣的属性。 但是这篇文章已经太麻烦了。 最后，我将介绍一个有趣的属性。