磁铁自古以来就已为人们所熟悉，但是铁磁性的物理学仍然是个谜。 现在，一个熟悉的难题使物理学家更接近回答问题
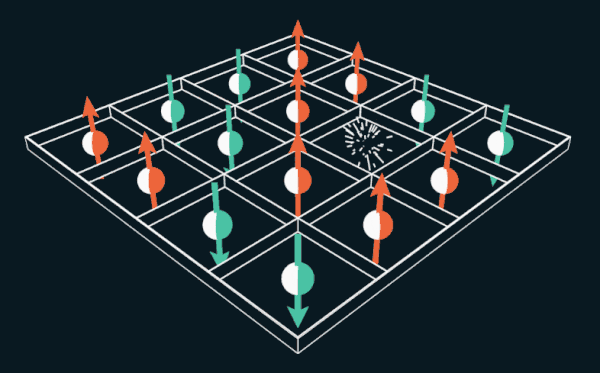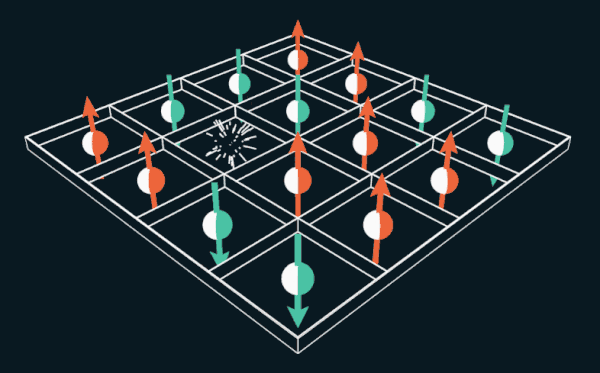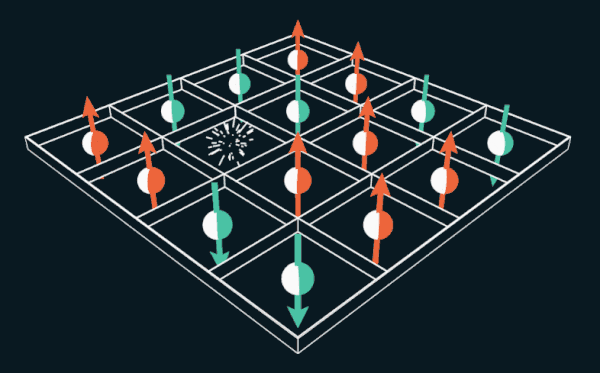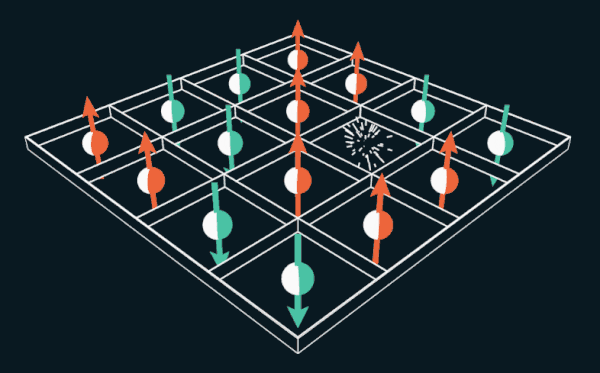15的游戏使玩家可以在网格内移动编号的图块。 如果用电子的自旋代替数字，则难题可以用来解释永磁体的工作原理。在1880年的几个月中，美国整个地区都沉迷于成瘾，这是以前没有人见过的类似物。 1880年3月12日，堪萨斯州因佩里亚的《每周新闻-民主》杂志写道：“全国各地实际上已经爆发了流行病。整个城市都被引诱，人们失去睡眠并发疯。” 流行病传播到欧洲，甚至与新西兰一起到达澳大利亚。
这种疾病已成为一种新的热情：不鼓励使用简单的机械益智玩具“ 15”。 它仍然是已知的，并且由4x4的正方形字段组成，您可以在其中移动15个编号的图块，以便按顺序排列它们。
以今天的标准来看，这款游戏似乎是过时的，但是在1880年，它才是普及的顶峰。 该报写道：“没有一个孩子能抗拒这种娱乐，没有一个成年人能如此坚强或自大以逃脱她的魅力。” 令人失望的原因可能是数学上已证明的事实，即该难题的一半配置都可以成功解决（这对受其影响的人可能是未知的）。
大约140年后的今天，人们对“ 15”游戏的兴趣再次恢复，但这一次并没有引起人们的注意，而只是一种理解似乎无关且复杂得多的难题的方法：磁铁是如何工作的。
永久磁铁，例如悬挂在冰箱门上的磁铁，会被诸如
铁磁性的现象吸引。 在铁磁体中，电子的自旋对齐，并且它们一起产生磁场。 更准确地说，诸如铁，钴和镍之类的金属表现出带磁性，因为它们的电子能够在材料内自由移动。 每个电子都有自己的磁矩，但是为了理解所有这些矩如何以及为什么排列在磁体中，有必要计算所有电子之间的量子相互作用，这很难做。
约翰·霍普金斯大学的物理学家威·李说：“地磁实际上是理论凝聚态物理中最大的挑战之一。”
但是，Lee和两个研究生Eric Bobrov和Keaton Stewbis可能已经更接近解决这个问题了。 他们使用数学难题“ 15”扩展了著名的定理，该定理描述了区域磁场的理想状态。 在《物理评论》 B上发表的最新
分析中，他们扩展了该定理，以解释一个更广泛，更现实的系统，这可能会导致更准确的磁体模型。
加利福尼亚大学圣地亚哥分校的物理学家
丹尼尔·阿洛瓦斯 （
Daniel Arovas）说：“这是一项很棒的工作。” “我特别喜欢这项工作，因为有关区域磁性的详细结果太少，而且过于分散。”
跳洞
在最基本的水平上，金属中的电子必须遵守两个主要限制。 首先，它们都带有负电荷，因此它们会互相排斥。 其次，要求电子遵守所谓的 保利原理，该原理假定两个粒子[具有半整数自旋/大约 [trans。]不能处于相同的量子状态。 这意味着具有相同自旋（与电子的磁矩成比例）的电子不能在金属原子中占据相同的状态。 自旋相反的两个电子可以。
事实证明，满足一组电子的相互排斥和保利原理的局限性的最简单方法是将它们分开并对齐其自旋-结果材料变成铁磁性。
但是，这只是一张简化的图片。 物理学家无法通过各个电子之间无数的量子相互作用来建立这种自旋排列的有组织模式的外观的详细模型。 例如，正如李所解释的那样，电子的波函数-一种对其量子性质的复杂数学描述-可以与另一个电子的波函数相混淆。 为了彻底了解单个粒子的行为如何导致诸如铁磁性这样的集体现象的出现，您必须监视系统中每个电子的波函数，同时在它们相互作用的过程中不断改变每个剩余电子的波函数。 实际上，这种普遍的纠缠使得不可能写下描述铁磁性所必需的完整而全面的方程式。
取而代之的是，包括李在内的物理学家正试图通过研究简化的，理想化的模型来收集信息，这些模型描述了铁磁性背后的物理原理。 特别是，她的最新作品扩展了50年前的重要发现。
在1960年代中期，来自地球另一侧的两位物理学家独立地得出了证据，证明了为什么电子应该排列并产生铁磁状态。 当时在剑桥大学工作的物理学家戴维·图尔斯（David Tules）最终获得了2016年诺贝尔奖，当时名古屋大学的物理学家长冈洋介（Yosuke Nagaoka）当时正访问圣地亚哥的加利福尼亚大学，分别于1965年和1966年发表了他们的证据。 。 他们的结果称为Nagaoki-Tules定理（或简称为Nagaoki定理），是基于位于原子晶格上的理想电子系统的。 因此，尽管它不能解释真实磁体的行为，但仍然很重要，原则上首次显示了为什么电子自旋应该对准。 而且，由于他们的分析是数学证据，因此它们是准确的，不会为典型的物理近似问题所困扰。
要理解该定理，请想象一个二维方格。 每个节点可以放置两个具有相反自旋的电子，但是该定理表明，将两个电子放置在一个位置将需要无限量的能量。 这样可以确保每个位置只有一个电子。 在这种配置中，每个电子都可以向上或向下引导其自旋。 它们不必对齐，因此这样的系统不应是铁磁体。
约翰·霍普金斯大学物理学家Wai Lee现在我们去除一个电子。 结果，将有一个称为孔的空位。 相邻的电子可以滑入一个孔中，留下一个新的空白空间。 另一个电子可以移动到新的空白处，从而留下另一个空穴。 实际上，在此示例中，一个孔从一个位置跳到另一个位置，并围绕网格移动。 Thules和Nagaoka发现，在这种情况下，当添加一个空穴时，电子将自发排列。 他们证明那将是能量最小的状态，即铁磁体的状态。
Arovas解释说，为了使系统进入最低能量的状态，空穴必须能够自由移动而不会干扰电子自旋的结构-这样的过程将需要额外的能量。 但是当空穴移动时，电子也必须移动。 为了使电子移动而不会干扰自旋的构型，必须将它们对齐。
东京大学的物理学家
押川正树说：“长冈定理是少数可以数学证明铁磁性个体情况的例子之一。” “但是从物理学的角度来看，所有这些都是非常人为的。”
例如，电子需要大量能量才能克服它们的相互排斥并在一个地方定居，但并非如定理所要求的那样无限。 另外，长冈和图勒斯绘制的图片仅适用于简单的格子：由正方形或三角形组成的二维格子，或三维立方格子。 在自然界中，铁磁性会在许多具有各种结构的金属中产生。
如果Nagaoka-Tules定理实际上解释了铁磁性，那么它应该适用于所有晶格。 李说，人们以为是。 “但是没有人提供真实，明确的证据。” 好吧，就是这样。
背砖
1989年，日本学院院大学物理学家Hal Tasaki扩展了该定理，发现只要晶格具有连通性这样的数学性质，该定理就适用。 以带有一个移动孔的方格的简单情况为例。 如果通过移动空穴可以复制自旋的任何构型，并保持电子数量且自旋方向同时上下，则满足连接条件。
但是，除了正方形和三角形格子以及三维立方体之外，尚不清楚在其他情况下是否满足连接条件-因此，该定理的适用范围有多大。
为了解决这个问题，Lee首先使用了六角形的蜂窝状网格。 她的学生Bobrov和Stubis在从事这项工作时，意识到它类似于十九世纪的躁狂症：拼图“ 15”。 从数字到背面，上下互换标签，拼图变得像长冈铁磁体一样，并且有一个沿电子晶格移动的孔。
当您有机会按任意顺序重新分配磁贴时，就可以解决难题，这完全符合连接条件。 因此，对于给定的晶格是否满足连通性条件的问题变成了是否有可能在这种结构的晶格上解决等效难题的问题。
事实证明，1974年，现在在加利福尼亚理工学院工作的数学家理查德·威尔逊（Richard Wilson）通过总结和解决所有光栅的“ 15”难题
来解决了这个问题 。 作为证明的一部分，他证明了在几乎所有不可分割的网格上（即使删除其中一个节点后，所有节点仍保持连接），您可以移动图块并获得任何配置，而移动次数仍保持偶数。 唯一的例外是单个多边形大于三角形，并且称为“图形θnull”，其中六边形中心的顶点连接到两个相对的顶点。
研究人员能够将Wilson的证明直接应用于Nagaoka-Tules定理。 他们证明，对于几乎所有晶格上的电子系统和单个空穴，包括二维蜂窝和三维菱形晶格这样的常见结构，满足连通性条件。 在任何情况下，在真正的铁磁体中都不会出现两个例外-大于三角形的多边形和θnull图。
孔爆炸
加州大学圣克鲁斯分校的物理学家
斯里拉姆·沙斯特里 （
Sriram Shastri）说，使用“ 15”难题是一种新鲜且可能富有成果的方法。 他说：“我喜欢他带来了一种新的语言，一种与图论的新联系的事实。” “我认为这是一个丰富的联系-将来它可能会成为思想的丰富来源。” 但是，尽管研究迈出了重要的一步，但仍然存在问题。
复杂的是，当移动的孔沿晶格移动需要采取奇数步长时，Nagaoki-Tules定理并不总是起作用。 也许最引人注目的问题是该定理要求存在一个准确的孔-不多也不少。 但是，金属充满孔；它们通常占据晶格的一半。
但是，物理学家试图将定理推广到具有许多孔的系统。 物理学家使用数值方法
表明 ，长冈的铁磁性似乎适用于有限大小的方格，其中最多30％是孔。 在当前的工作中，研究人员将精确的分析技术应用于二维蜂窝和三维菱形格子。 只要孔的数量不超过蜂窝状的1/2度，菱形格子的2/5度，显然存在长木铁磁性。
这些精确的解决方案可以产生更完整的区域磁模型。 Lee说：“这只是为未来研究设定严格的数学起点的一小步。”