⛹️ 🕺🏼 🥣 学校教科书II中的任务 🚖 🙆🏼 ◻️

第一部分
第二部分
第三部分

本文讨论了估计可接受值范围的方法以及该方法与包含模块的任务的关系。

解决某些问题时，有必要考虑期望值的范围。

考虑解决不等式的估计方法 。

假设每单位商品的价格在5到10卢布之间。给出上限意味着确定所需数量可以采用的最大值。对于两个商品的价格不超过10的商品，最高估计值为10 + 10 = 20 。

从问题概要文件概要文件 MI中考虑问题巴什马科娃
37.已知变量估计

$x$ 和

$ inline $ y：0 <x <5，2 <y <3。$ inline $

为以下表达式打上最高分：
1。

年

$2x + 3年$
2。

$xy$

解决问题5和6的指南

要计算分数表达式，必须使用以下数值不等式的属性：

如果 $内联$ a <b $内联$ 两个数字都是正数 $ inline $ \ frac {1} {a}> \ frac {1} {b} $ inline $

5，

$\ frac {1} {y}$
6。

$\ frac {x} {y}$

解决问题8和9的说明

要评估负值，必须使用数值不等式的以下属性：
如果

$内联$ a <b $内联$ 两个数字都是正数

$ inline $ -a> -b $ inline $

8。

$x-y$
9。

$3x-2y$

通常，无穷数量的分析使用评估标准。模块（作为邻域）可以在限制的定义中找到应用。

$$显示$$ \左| x_ {n} -a \右| <\ varepsilon $$显示$$

考虑“微分和积分学课程” 363（6）中的示例

易于设置行发散
$\ sum \ frac {1} {\ sqrt {n}} = 1+ \ frac {1} {\ sqrt {2}} + \ frac {1} {\ sqrt {3}} + ... + \ frac {1} {\ sqrt {n}} + ...$

实际上，由于其成员减少，因此第n个部分和
$$ display $$ 1+ \ frac {1} {\ sqrt {2}} + ... + \ frac {1} {\ sqrt {n}}> n \ cdot \ frac {1} {\ sqrt {n }} = \ sqrt {n} $$显示$$

并随着无限增长 $n$ 。

为了证明

$1+ \ frac {1} {\ sqrt {2}} + ... + \ frac {1} {\ sqrt {n}}$ 真的更多

$\ sqrt {n}$ ，您需要对此表达式进行较低的估算。我们得到不等式的系统

$$显示$$ \左\ {\！\开始{aligned}＆\ frac {1} {\ sqrt {n-1}}> \ frac {1} {\ sqrt {n}} \\＆\ frac { 1} {\ sqrt {n-2}}> \ frac {1} {\ sqrt {n}} \\＆\ frac {1} {\ sqrt {n-3}}> \ frac {1} {\ sqrt {n}} \\＆... \结束{aligned} \对。 $$显示$$

加上该系统的所有不等式后，我们得到

$$ display $$ 1+ \ frac {1} {\ sqrt {2}} + \ frac {1} {\ sqrt {3}} + ... + \ frac {1} {\ sqrt {n}}> \ frac {1} {\ sqrt {n}} + \ frac {1} {\ sqrt {n}} + \ frac {1} {\ sqrt {n}} + ... + \ frac {1} {\ sqrt {n}} = n \ cdot \ frac {1} {\ sqrt {n}} $$显示$$

这证明该系列有所不同。

对于谐波系列，此方法不起作用，因为

$n$ 偏偏谐波系列

$$ display $$ 1+ \ frac {1} {2} + \ frac {1} {3} + ... + \ frac {1} {n}> n \ cdot \ frac {1} {n} = 1 $$显示$$

回到任务

38.计算金额（“ 5至15岁儿童的任务”）

$\ frac {1} {1 \ cdot2} + \ frac {1} {2 \ cdot3} + \ frac {1} {3 \ cdot4} + ... + \ frac {1} {99 \ cdot100}$

（错误不超过答案的1％）

该系列的最高估价

$\ frac {n} {n + 1}$ 给出数字1。

放弃第一学期

$\ frac {1} {1 \ cdot2}$

(define series_sum_1 ( lambda (n) (if (= n 0) 0 (+ (/ 1.0 (* (+ n 1.0 )(+ n 2.0))) (series_sum_1(- n 1.0))) ) ) ) (writeln (series_sum_1 10)) (writeln (series_sum_1 100)) (writeln (series_sum_1 1000)) (writeln (series_sum_1 10000)) (writeln (series_sum_1 100000)) (writeln (series_sum_1 1000000))

我们得到

$1-\ frac {1} {1 \ cdot2} = \ frac {1} {2}$
0.4166666666666666363
0.49019607843137253
0.4990019960079833
0.4999000199960005
0.49999000019998724
0.4999990000019941

您可以在此处登录ideone.com

Python中的相同算法

 def series_sum(n): if n==0: return 0 else: return 1.0/((n+1.0)*(n+2.0))+series_sum(n-1.0) print(series_sum(10)) print(series_sum(100))

链接到ideone.com

删除前两个词

$\ frac {1} {1 \ cdot2} + \ frac {1} {2 \ cdot3}$

 (define series_sum_1 ( lambda (n) (if (= n 0) 0 (+ (/ 1.0 (* (+ n 2.0) (+ n 3.0))) (series_sum_1(- n 1.0))) ) ) ) (series_sum_1 1000000)

我们将得到0.33333233333632745
该系列的部分和在上方有界。

正行始终有一个数量；如果序列的部分和在上面有界，则该和将是有限的（因此序列收敛），否则是无限的（且序列发散）。

我们随着n的增加来计算谐波序列的总和

 #lang racket (define series_sum_1 ( lambda (n) (if (= n 0) 0 (+ (/ 1.0 n) (series_sum_1(- n 1.0))) ) ) ) (series_sum_1 10) (series_sum_1 100) (series_sum_1 1000) (series_sum_1 10000) (series_sum_1 100000) (series_sum_1 1000000)

我们得到：
2.9289682539682538
5.187377517639621
7.485470860550343
9.787606036044348
12.090146129863335
14.392726722864989

扔掉

$n$ 谐波序列的初始项。
证明（使用下限）

$$显示$$ \ frac {1} {n + 1} + \ frac {1} {n + 2} + ... + \ frac {1} {2n}> \ frac {1} {2} $$显示$$

如果舍弃前两项，则谐波序列的其余成员按 $2,4,8，...，2 ^ {k-1}，...$ 每个成员
$；；$
$\ frac {1} {3} + \ frac {1} {4}； \ frac {1} {5} + \ frac {1} {6} + \ frac {1} {7} + \ frac {1} {8}； \ frac {1} {9} + ... \ frac {1} {16}; ...;$

$，$
$\ frac {1} {2 ^ {k-1} +1} + ... + \ frac {1} {2 ^ {k}}; ...，$

那么这些金额中的每一个都会更大 $\ frac {1} {2}$ 。
...我们看到部分和不能超出上述范围：该序列具有无限和。

我们计算通过丢弃获得的部分金额

$2 ^ {k}$ 条款。

 #lang racket (* 1.0 (+ 1/3 1/4)) (* 1.0 (+ 1/5 1/6 1/7 1/8)) (* 1.0 (+ 1/9 1/10 1/11 1/12 1/13 1/14 1/15 1/16))

我们得到：
0.583333333333333434
0.6345238095238095
0.6628718503718504
我们编写了一个程序来计算

$\ frac {n} {2}$ 之前

$n$ 在哪里

$n = 2 ^ {k}$ 在

$k \ in \ mathbb {N}$

 #lang racket (define (Hn n ) (define half_arg (/ n 2.0)) (define (series_sum n) (if (= n half_arg ) 0 (+ (/ 1.0 n) (series_sum(- n 1)) ) ) ) (series_sum n) ) (Hn 4) (Hn 8) (Hn 16) (Hn 32)

我们得到：
0.583333333333333333
0.6345238095238095
0.6628718503718504
0.6777662022075267

您可以通过以下链接在线登录
对于范围

左 ； 右

$\左[1 + 2 ^ {70}； 2 ^ {71} \右]$ 我们得到0.693147 ...
在此处查看Wolfram Cloud中的mojo。

此递归算法导致快速堆栈溢出。
本文提供了一个使用迭代算法计算阶乘的示例。我们修改了这种迭代算法，以便计算出一定范围内的部分和Hn 。称这些边界为a和b

 (define (Hn ab) (define (iteration product counter) (if (> counter b) product (iteration (+ product (/ 1.0 counter)) (+ counter 1)))) (iteration 0 a))

下限是数字

$1 + 2 ^ {k}$ ，上限是数字

$2 \ cdot 2 ^ {k}$
我们编写一个函数来计算两个的幂

 (define (power_of_two k) (define (iteration product counter) (if (> counter k) product (iteration (* product 2) (+ counter 1)))) (iteration 1 1))

我们将（+ 1（power_of_two k））替换为下边界，并使用函数（* 2（power_of_two k））或其等效函数（power_of_two（+1 k））作为上边界
重写函数Hn

 (define (Hn k) (define a (+ 1 (power_of_two k)) ) (define b (* 2 (power_of_two k)) ) (define (iteration product counter) (if (> counter b) product (iteration (+ product (/ 1.0 counter)) (+ counter 1)))) (iteration 0 a ))

现在您可以计算大数值的Hn

$k$ 。

我们用C编写了一个程序，该程序测量计算Hn所需的时间。我们将使用<time.h>标准库中的clock（）函数
Habré上有一篇有关测量处理器时间的文章。

 #include <math.h> #include <stdio.h> #include <time.h> int main(int argc, char **argv) { double count; // k  1+2^30  2^31 for(unsigned long long int i=1073741825 ;i<=2147483648 ;i++) { count=count+1.0/i; } printf("Hn = %.12f ", count); double seconds = clock() / (double) CLOCKS_PER_SEC; printf("  %f  \n", seconds); return 0; }

通常，在线ide将运行程序的执行时间限制为五秒钟，因此只能在某些在线ide中（例如，在onlinegdb.com或repl.it中）检查该程序。
对于从1 + 2 ^ 30到2 ^ 31的k，操作时间约为5秒。
对于从1 + 2 ^ 31到2 ^ 32的k，操作时间约为10秒。
对于从1 + 2 ^ 32到2 ^ 33的k，操作时间约为20秒。
对于从1 + 2 ^ 33到2 ^ 34的k，操作时间约为40秒。
对于从1 + 2 ^ 34到2 ^ 35的k，操作时间将超过一分钟。
...
对于从1 + 2 ^ 45到2 ^ 46的k，操作时间将超过24小时。

假设对于从1 + 2 ^ 30到2 ^ 31的k，算法的执行时间为〜2秒。
然后，对于k = 2 ^（30 + n），算法的执行时间为2 ^ n sec。（在

$n \ in \ mathbb {N}$ ）
该算法具有指数复杂度。

返回模块。
在积分计算中，该模块用于公式中

对

$\ int \ frac {1} {x} dx = \ int \ frac {dx} {x} = ln \ left | x \对| + C$

在哈布雷（Habré）上有一篇文章《最自然的对数》，在该对数中考虑了该积分并根据其对数的计算

$e$ 。

公式中模块的存在

左 对

$\ int \ frac {dx} {x} = ln \左| x \对| + C$ 在“微分和积分学课程”中进一步得到证实

如果... $内联$ x <0 $内联$ ，那么通过区分就很容易验证 $\左[ln（-x）\右]'= \压裂{1} {x}$

积分的物理应用 $\ int \ frac {dx} {x}$

该积分用于计算圆柱形电容器的极板电位差。

“电和磁”：

板之间的电势差可通过积分找到：
$\ varphi_ {1}-\ varphi_ {2} = \ int \ limits_ {R_ {1}} ^ {R_ {2}} E（r）dr = \ frac {q} {2 \ pi \ varepsilon_ {0} \ \ varepsilon l} \ int \ limits_ {R_ {1}} ^ {R_ {2}} \ frac {dr} {r} = \ frac {q} {2 \ pi \ varepsilon_ {0} \ varepsilon l} ln \压裂{R_ {2}} {R_ {1}}$

（ $R_ {1}$ 和 $R_ {2}$ -内板和外板的半径）。

自然对数符号此处未使用模块符号

$ln \左| \ frac {R_ {2}} {R_ {1}} \右|$ 因为

$R_ {1}$ 和

$R_ {2}$ 严格肯定，这种记录形式是多余的。

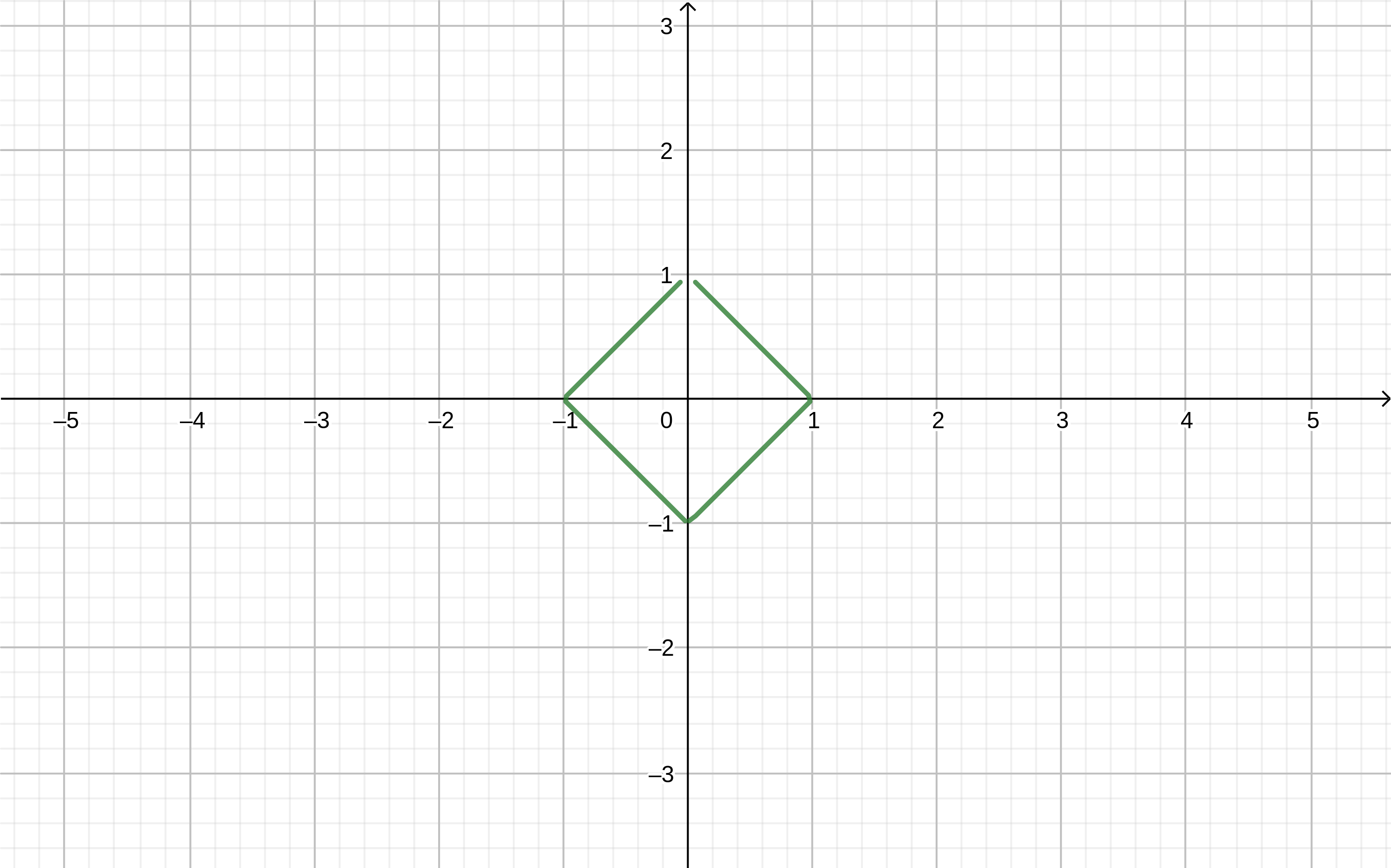
“模块化”图纸

使用模块，您可以绘制各种形状。

如果在geogebra程序中编写公式

$abs（x）+ abs（y）= 1$ 我们得到

您可以绘制更复杂的形状。例如，让我们在WolframAlpha云中绘制“蝴蝶”

$\ sum \ frac {\左| x \对| } {n- \左| x \对| } + \ frac {\左| x + n \对| } {n} + \ frac {\左| x-n \对| } {n}$

绘制[总和[abs（x）/（n-abs（x））+ abs（x + n）/（n）+ abs（xn）/（n），{n，1,20}]，{x， -60.60}]
在这个表达中

$n$ 介于

$1$ 之前

$20$ ，

$x$ 介于

$-60$ 之前

$60$ 。
链接到图片。

书籍：

M.I.“个人资料取向的任务书” 巴什马科夫
普通物理课程：3卷T。2。萨韦利耶夫

学校教科书II中的任务

积分的物理应用 int fracdxx \ int \ frac {dx} {x}

“模块化”图纸

书籍：

More articles:

积分的物理应用 $\ int \ frac {dx} {x}$